基于CTM和Beam-Column Joint Element的梁柱节点核心区抗剪仿真

2020-07-21唐智强黄世涛

土木工程与管理学报 2020年3期

唐智强，黄世涛，马健

(华中科技大学土木工程与力学学院，湖北武汉 430074)

钢筋混凝土梁柱节点的抗震能力是决定框架结构破坏形态和整体地抗震破坏性能的关键因素，其抗震能力的计算和仿真也一直是框架结构整体抗震性能的重点和难点[1]。在诸多钢筋混凝土梁柱节点抗剪强度计算理论模型、钢筋混凝土梁柱节点核心区单元模型、钢筋混凝土梁柱节点抗震仿真分析软件和平台中，目前应用最广泛的是美国华盛顿大学Lowes和Mitra两位学者提出基于转动铰模型的二维平面超级节点单元模型(Super Model)，及其基于OpenSees平台下建立的Beam-Column Joint Element单元和仿真计算程序[2～4]。该模型计算的前置条件和最关键参数是需要根据理论计算模型确定钢筋混凝土梁柱节点核心区的理论抗剪强度应力应变本构，Mitra推荐采用斜压杆法(Compression Strut Model，CTM)[5]或斜压场法(Modified Compression Field Theory，MCFT)[6]进行计算。

为研究基于CTM和Beam-Column Joint Element单元的钢筋混凝土梁柱节点核心区抗震仿真计算，本文先分析了CTM的计算原理和局限性，并对原计算模型进行调整。之后通过一系列试验数据验证了调整前后模型在常规参数组合下计算结果与试验结果均基本一致。之后通过计算基于核心区配箍率、主梁配筋率、钢筋强度、轴压比共4个参数耦合下共计2560个模型，并通过参数分析得出调整前后CTM在不同参数下核心区抗剪强度的变化规律。最后通过对比参数分析计算规律与试验计算规律，证明调整后模型更为准确。

1 CTM简介

图1为CTM的计算简图[5]。根据钢筋混凝土梁、柱的正截面抗弯承载力理论，梁柱端在水平地震力作用下，各个梁柱端截面会形成混凝土受压区，图1中Ccu和Ccb为柱端混凝土受压区所受的压力合力，Ccr和Ccl为梁端混凝土受压区的压力合力，Ccu和Ccl在核心区的左上角形成指向右下角的合力，而Ccb和Ccr的合力指向左上角，两个合力的共同作用，在节点核心区的混凝土中形成一个沿核心区对角线分布的斜向压应力场，这就是斜压杆机构。

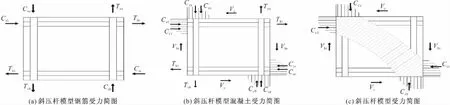
图1 斜压杆模型

CTM主要基于以下假定：

(1)所有剪切应力均沿主压杆传播；

(2)斜压杆压应力方向与剪切应力方向一致且等效；

基于假定(1)(2)可得到：

(1)

式中：τstrut,t为根据斜压杆模型计算出的剪切块的剪应力，其是一条随着剪切应变变化的曲线；w为有效核心区宽度；αstrut为主压杆方向与水平方向夹角，由于剪切块的剪切变形属于微小变形，所以αstrut也可认为不变；fc-strut,t为有效压杆应力，但不等于混凝土抗压强度；wstrut为压应力场有效宽度。

据此可得到：

(2)

式中：cb为梁方向的等效受压区宽度；cc为柱方向的等效受压区宽度。式(2)即为CTM的主要计算原理和公式[5]。

2 CTM用于定参讨论

文献[3,4,7]在用CTM对钢筋混凝土梁柱节点核心区抗剪强度计算时，对于主压杆应力方向均依据核心区变形为微小剪切变形，简单认为主压应力方向与等效的剪切应力方向一致且沿对角线方向。

但基于上述CTM计算原理对剪切应力方向和斜压杆压应力方向分别进行受力分析可知，剪切应力方向取决于核心区剪切变形的情况，斜压杆应力方向为梁、柱压应力的合力方向。而梁柱节点核心区剪切变形如图2a所示，梁截面和柱截面分别绕变形轴发生变形。需要强调的是，梁截面和柱截面的变形轴不一定与几何轴重合，且变形轴距离角点位置亦不一定相等。截面变形对应到核心区变形为一种剪切变形，该剪切变形并不一定是理想剪切变形(即变形后变形面为平行四边形)。但考虑各个梁柱截面的变形大部分时候满足平截面假定，且对于梁柱节点变形为微小变形，其变形可近似等效为理想剪切变形。对于理想剪切变形，其剪切应力方向沿对角线方向，其与梁方向夹角α=arctan(H/D)。

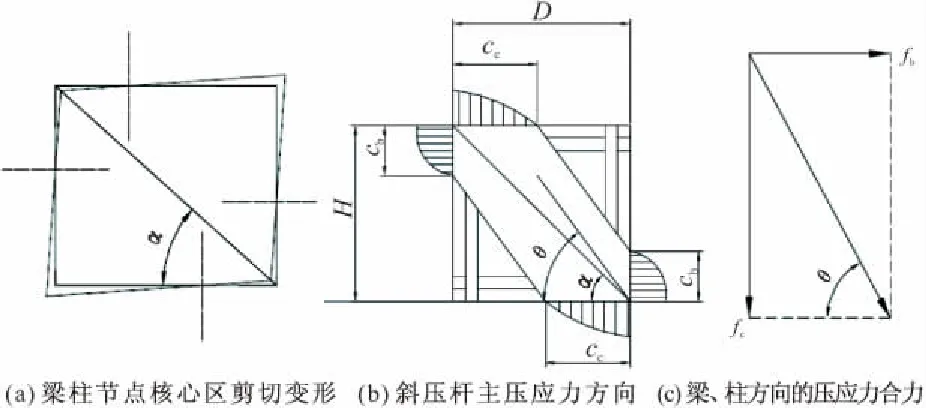
图2 核心区剪切变形示意

而对于斜压杆主压应力方向，如图2b所示，考虑cb，cc分别表示等效受压区宽度，而核心区的混凝土抗压强度(本构)一致，故梁、柱方向的压应力与cb，cc成正比对应。考虑斜压杆主压应力为梁、柱方向压应力的合力，作简单受力合成可知(见图2c)，其方向与梁方向夹角θ=arctan(cc/cb)。

基于以上分析可知，斜压杆压应力方向与剪切应力方向并不一定一致，剪切应力为斜压杆压应力在对角线方向的投影。据此，式(1)可调整为：

(3)

事实上，如果不考虑核心区剪切变形的近似，按核心区实际变形最终得出的剪切应力方向必然与主压应力方向一致。这是因为同一构件同一受力状态下从变形条件和受力条件得出的等效应力方向必然一致。但当采用Opensees软件中的Beam-Column Joint Element单元对梁柱节点进行非线性低周往复运动模拟的定参和仿真分析，受单元原理的Super Model单元模型本身的限制，必须将核心区按理想剪切变形考虑方可进行计算。故须将核心区的剪切变形等效为理想剪切变形，学者Mitra在计算时将二者进行简单等效[3,4]。实际深入分析CTM模型和Super Model单元模型的原理可知，等效时应考虑剪切应力方向与对角线方向的角度差，即图2b中的θ-α。

同时考虑对于基于往复荷载下的滞回性能作为梁柱节点抗震性能的判定标准，考虑对角线方向上抗剪强度的投影做为抗震破坏性能更合理。这是因为CTM下主压应力方向与对角线方向不重合的分析是基于单向静力加载，其裂缝亦为略偏差于对角线方向的斜裂缝(如图3a所示[8～13])。但在低周往复荷载作用下，随着正向和反向裂缝的反复加载，混凝土裂缝方向均会逐步趋向于对角线方向(如图3b所示[8～13])。故在低周往复荷载作用下，以对角线方向上抗剪强度的投影作为剪切破坏的控制条件更为合理，即Laura和Mitra提出的Super Model单元模型相比于CTM模型计算结果更能有效代表钢筋混凝土梁柱节点的实际抗震性能。

图3 静力与拟静力作用下核心区破坏示意

3 模拟验证

为检验调整前后CTM计算结果的正确性，选用多伦多大学在20世纪80～90年代所完成的一系列试验进行对比分析，具体构件参数详见文献[6,14,15]，文献中试件PV20建模计算结果与试验对比结果如图4所示。图中蓝色实线为调整前模型计算结果，红色虚线为调整后模型计算结果，黑色带星实线为文献中试验结果。从图4可以看出本文建模计算结果与试验吻合较好。同时可以看出，调整后模型比调整前的模型计算结果略微偏小，这是因为试件PV20的配筋情况下柱方向上受压区高度与梁方向上受压区高度基本一致，调整前模型的主压应力方向与对角线方向角度差很小，故投影到对角线方向的折减较小。

图4 本文CTM建模计算结果与试验对比

为进一步检验调整前后CTM用于OpenSees平台下Beam-Column Joint Element单元定参的正确性，基于OpenSees平台建立仿真分析模型并与试验结果进行对比验证。试件选用作者参与课题试件[8～13]，典型试件SP00的尺寸及配件如图5所示，SP00在拟静力作用下滞回曲线和仿真分析拟合下滞回曲线对比如图6所示。从图6可以看出，调整前后模型定参下仿真分析计算结果与试验结果均吻合良好，调整后模型计算结果比调整前计算结果略微偏小。这是因为典型试件的柱方向上与梁方向上受压区高度差别不大，对调整后模型计算的核心区应力应变曲线比调整前略微偏小导致。同时这也证明该模型用于该平台建模分析的正确性与可行性。

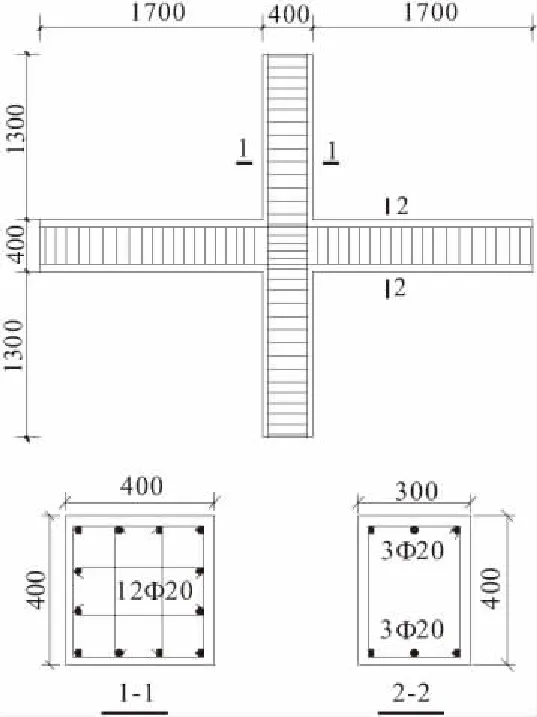
图5 SP1构件尺寸及配筋/mm

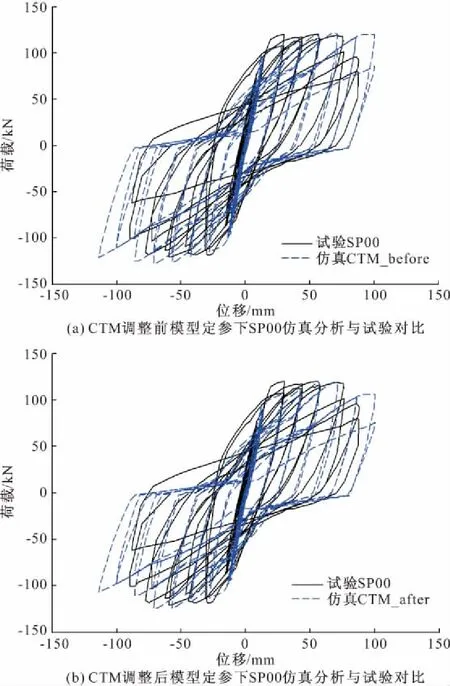
图6 CTM调整前后模型定参下SP00仿真分析与试验对比

4 参数分析

为了分析调整前后CTM在各种参数组合下的适用性，基于作者参与课题试验试件，对调整前后的CTM进行参数分析。

分析参数包括核心区配箍率、主梁配筋率、钢筋强度、轴压比共4个参数。具体选用参数组合如表1所示。

表1 参数分析取值

基于以上参数耦合共计需要计算2560个模型。其中，试件SP00对应设计参数核心区配箍6Φ10、主梁配筋3Φ20、钢筋牌号为HRB500E、轴压比0.28，为参数分析的中位组合，作为对比的基准参数。为简化结果提取过程，基于边界圆法对计算结果进行整理，具体步骤为：

(1)基于基准试件的计算结果进行分析，分析在其它3个参数不变的情况下，1个参数的变化规律；

(2)找到规律后，对另外3个参数进行最不利组合，验证变化参数对应规律的有效性，如果在任何最不利组合下该规律均适用，则可判定该规律对于参数分析范围内的试件均有效。

4.1 调整前CTM参数分析

图7为调整前CTM计算SP00试件的核心区抗剪应力应变曲线。从图中曲线可以看出，抗剪强度在应变0.3%范围内线性增加，之后增加速率开始变缓，这是因为在应变0.3%之后受拉区混凝土逐渐开裂破坏，不再产生拉应力。当应变达到1%左右时抗剪强度达到峰值，之后逐渐下降，下降段无明显破坏点，计算过程中计算到应变6%停止。但实际试验中，大部分试件在应变3%～4.5%已经完全破坏，无法继续加载。

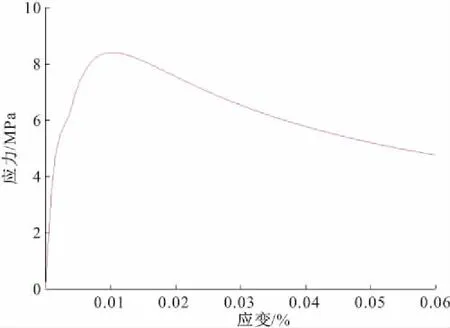
图7 调整前CTM计算基准试件应力应变曲线

进一步分析单个参数对CTM计算结果的影响，计算在主梁配筋3Φ20、钢筋强度HRB500E、轴压比0.28下(基准参数下)，核心区配箍从2Φ10(SP01_1)到12Φ10(SP01_10)的应力应变曲线。该组试件命名为SP01组，单个试件依次命名为SP01_1至SP01_10，计算结果如图8a所示。同时可以看出，SP01_5的设计参数与SP00设计参数一致，这一组试件的计算结果可以有效反映出基于SP00设计条件下核心区配箍变化对CTM计算结果的影响规律。

对计算结果进行比较可以看出，不同应力应变曲线的形状与变化规律大致一致，只是随着核心区配箍逐渐增大计算结果相应增加。其它参数组合下曲线形状与变化规律亦基本相同，在此不一一列出。从此图8a可以看出，对于核心区抗剪强度应力应变曲线，因为其曲线形态基本一致，故可取其抗剪强度最大值与平均值做为特征值进行分析。将其应力最大值与平均值提取后如图8b所示，可以看出其最大值和平均值均随着核心区配箍增加而加大，其变化规律与图8a完全一致。而应变最大值线性增加，平均值增加先快速后线性。考虑到不同试件的破坏应变各不相同，破坏应变之后的数据无实际意义，该应力应变曲线的最大值比平均值更具说服力，故本文后续只重点分析曲线的最大值变化规律。

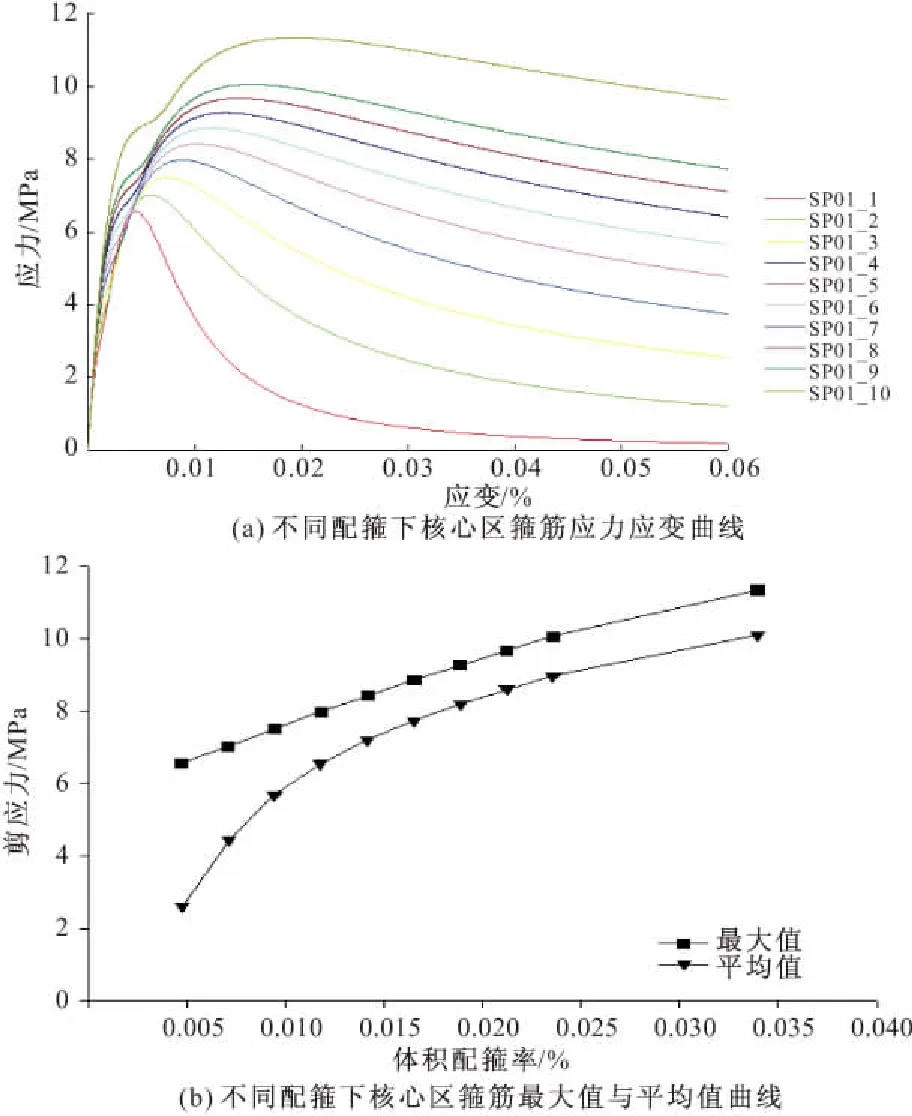
图8 调整前CTM核心区配箍应力应变曲线

图9为在基准参数下，任意单个参数在基准参数组合下的抗剪强度最大值比较图，其中横坐标为基于基准参数的无量纲化结果。从图中可以看出，4个参数的增大均会导致核心区抗剪强度增加，其增加规律接近于线性增加。为验证以上规律的有效性，对任意参数取另外3个参数最不利组合进行参数分析，其中对于核心区轴压比的参数组合如图10所示。从图10可以看出，在各种参数组合下，不同轴压比的试件的抗剪强度最大值变化情况与中数组基本一致。其它参数变化规律亦与此类似，在此不一一列举。

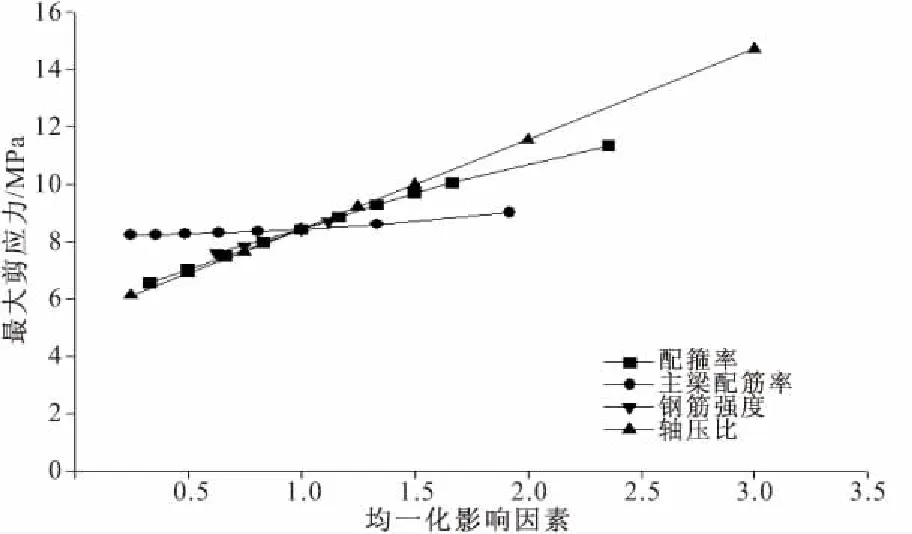
图9 调整前CTM基准参数变化规律

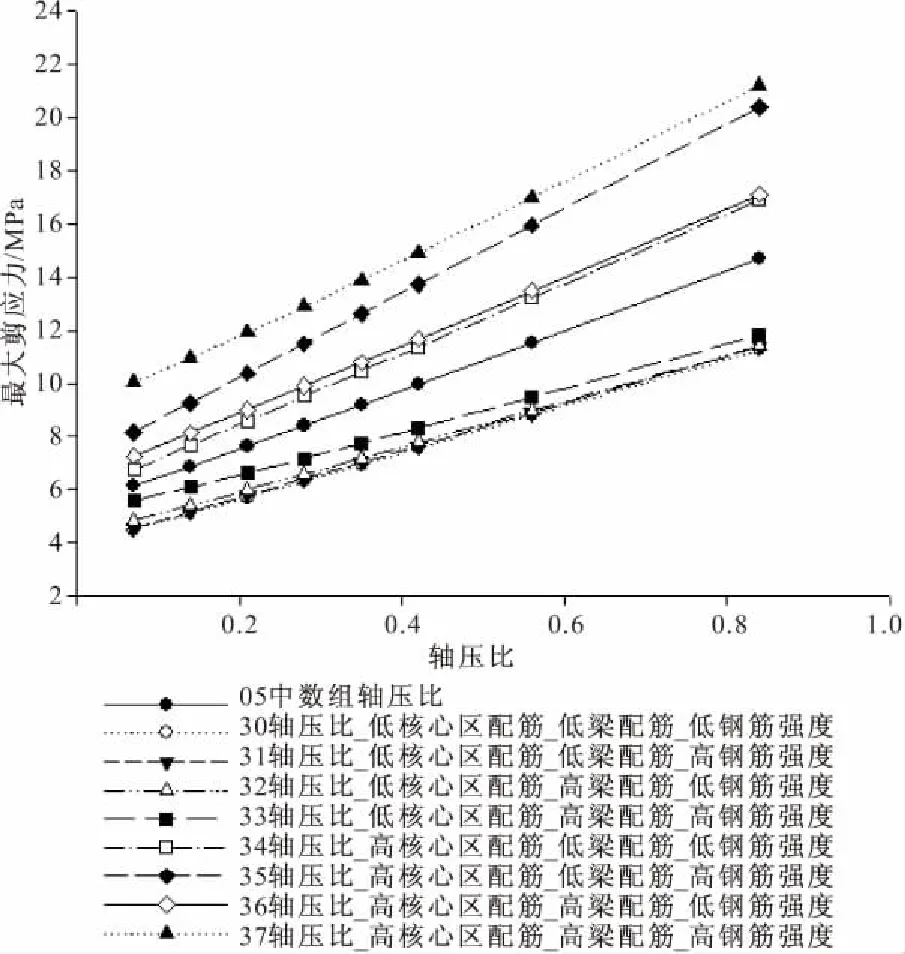
图10 调整前CTM轴压比在各参数组合下的变化规律

综合以上分析可以得出，调整前CTM计算的核心区抗剪强度变化规律如下：

(1)抗剪强度应力应变曲线在应变0.3%范围内线性增加，之后逐渐增加到破坏应变，再缓慢下降，无破坏段或破坏点；

(2)在各种参数组合下，核心区配箍率、主梁配筋率、钢筋强度、轴压比的增加均会导致核心区抗剪强度的增加，增加基本呈线性规律，对核心区影响从大到小的参数依次为轴压比、核心区配箍、钢筋强度、梁配筋率。各参数斜率如表2所示。

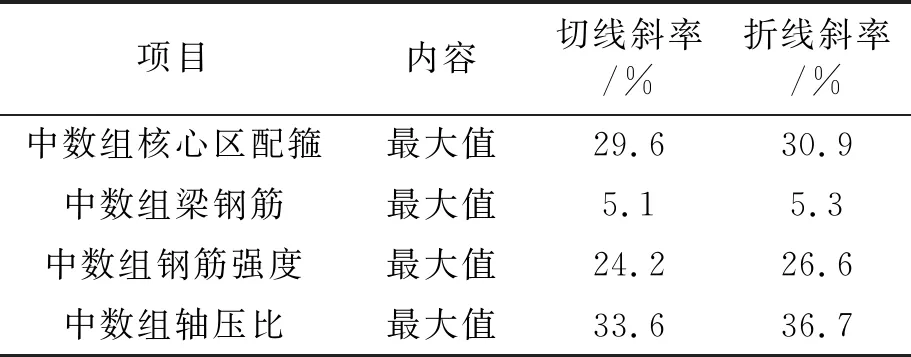
表2 调整前CTM各参数中数组最大值斜率

以上斜率是对影响核心区抗剪强度程度的一种定量描述。以核心区配箍率为例，表2中斜率的物理含义为：在参数分析范围内，核心区配箍率每增加100%，核心区抗剪强度增加30%。

4.2 调整后CTM参数分析

调整后CTM参数分析过程与调整前基本一致，基准参数下单个参数变化计算得到的应力最大值规律如图11所示。与图9对比可以得到以下结论：

(1)总体抗剪强度均略有下降；

(2)核心区配箍、主梁配筋、钢筋强度变化规律与调整前基本一致，调整后模型在轴压比增大时，抗剪强度呈现先增大后减小的规律。

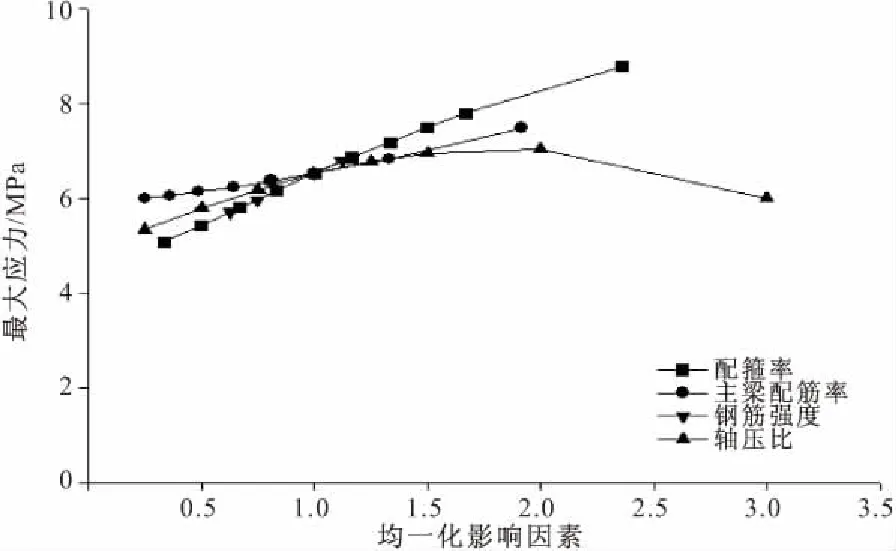
图11 调整后CTM基准参数变化规律

为验证以上结论，对轴压比与另外三种参数的最不利组合进行参数分析，其计算结果如图12所示。从图12可以看出，在核心区配箍率、主梁配筋率、钢筋强度各种参数组合下，轴压比对抗剪强度的影响均为先增大后减少，最合适的轴压比一般在0.55左右。这是因为，随着轴压比的增大，柱方向受压区高度不断增大，主压应力与对角线方向偏角亦不断增大。

4.3 调整前后结果对比

对比调整前后的参数分析结果可以发现，调整前后的差别主要集中在轴压比增大对核心区抗剪强度的影响。这是因为其它参数不太影响受压区高度，故不影响合力方向角，从而使得调整前后计算结果无显著区别。

对于轴压比参数的影响，调整前CTM计算结果表现为线性增加规律，调整后CTM计算结果表现为先增大后减小的规律，拐点大约在0.55左右。对比国内外相关试验研究，其结果均显示随着轴压比增大，核心区抗剪强度先增大后减小的试验规律[1,16]。以框架节点专题研究组的试验结果为例，轴压比从0.5增大到0.84时会有显著拐点[1]，并建议轴压比不要大于0.5。故从这个角度分析，调整后模型更能有效反映出轴压比变化对核心区抗剪应力应变曲线的影响。在轴压比较大的情况下计算结果更准确，仿真分析定参更适用。