大跨度钢桁架拱桥施工阶段抗震性能分析
2020-07-21姚昌荣李亚东
周 文, 姚昌荣, 李亚东
(西南交通大学土木工程学院,四川成都 610031)
桥梁是道路关键节点,一旦垮塌,抢修临时便道恢复交通十分困难,其抗震安全性尤为重要。钢桁架拱桥造型优美、跨越能力大,在我国得到越来越多的应用。目前已经有大量学者对钢桁架拱桥的抗震性能进行过专门研究[1-4],但这些研究基本针对成桥状态的桥梁,对施工阶段桥梁的研究甚少。侯远利[5]以某钢筋混凝土拱桥为例,较为细致的研究了该桥施工阶段的抗震性能。Wilson[6]研究了处于悬臂施工阶段的斜拉桥在地震作用下的响应,Benjumea[7]分析了处于悬臂施工阶段的矮塔斜拉桥的地震易损性,Wen[8]则提出了一种针对处于施工阶段斜拉桥的振动控制方案。目前还没有学者对施工阶段钢桁架拱桥抗震性能进行过专门研究。
大跨度钢桁架拱桥结构复杂,施工精度要求高,施工周期往往长达数年,不能忽略其在长期施工中遭遇地震的可能。本文以某大跨钢桁架拱桥为工程背景,对施工阶段钢桁架拱桥的抗震性能进行研究。
1 模型建立
1.1 工程概况
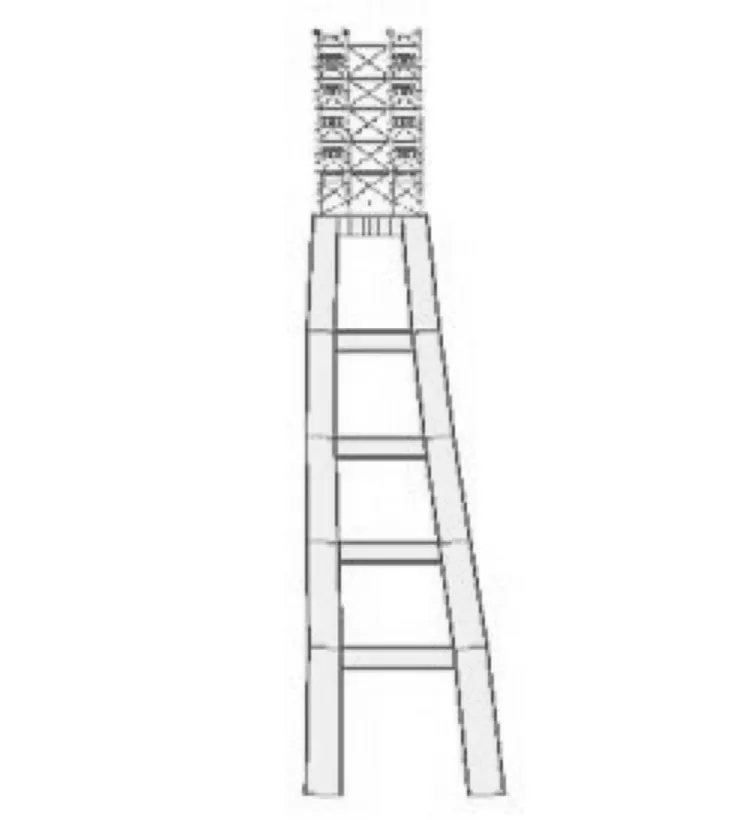
本文以一座主跨490m提篮式上承钢桁架拱桥为工程背景,该桥矢高109.5m,矢跨比1/4.475,拱轴线采用悬链线,拱轴系数2.0,拱肋内倾角3.657 8 °,拱脚处拱肋间距为32m,拱顶处拱肋间距为18m。钢桁拱采用4片桁设计,上、下弦杆截面高、宽皆为2.0m。4片桁每两片组成一肋,每肋的两片桁间距3.4m,通过横杆连接成整体。桁高为变高度,拱脚为16m,拱顶11m。弦杆采用箱型带肋截面,腹杆截面采用H型,主拱之间采用K型横向联接系,结构简图见图1。
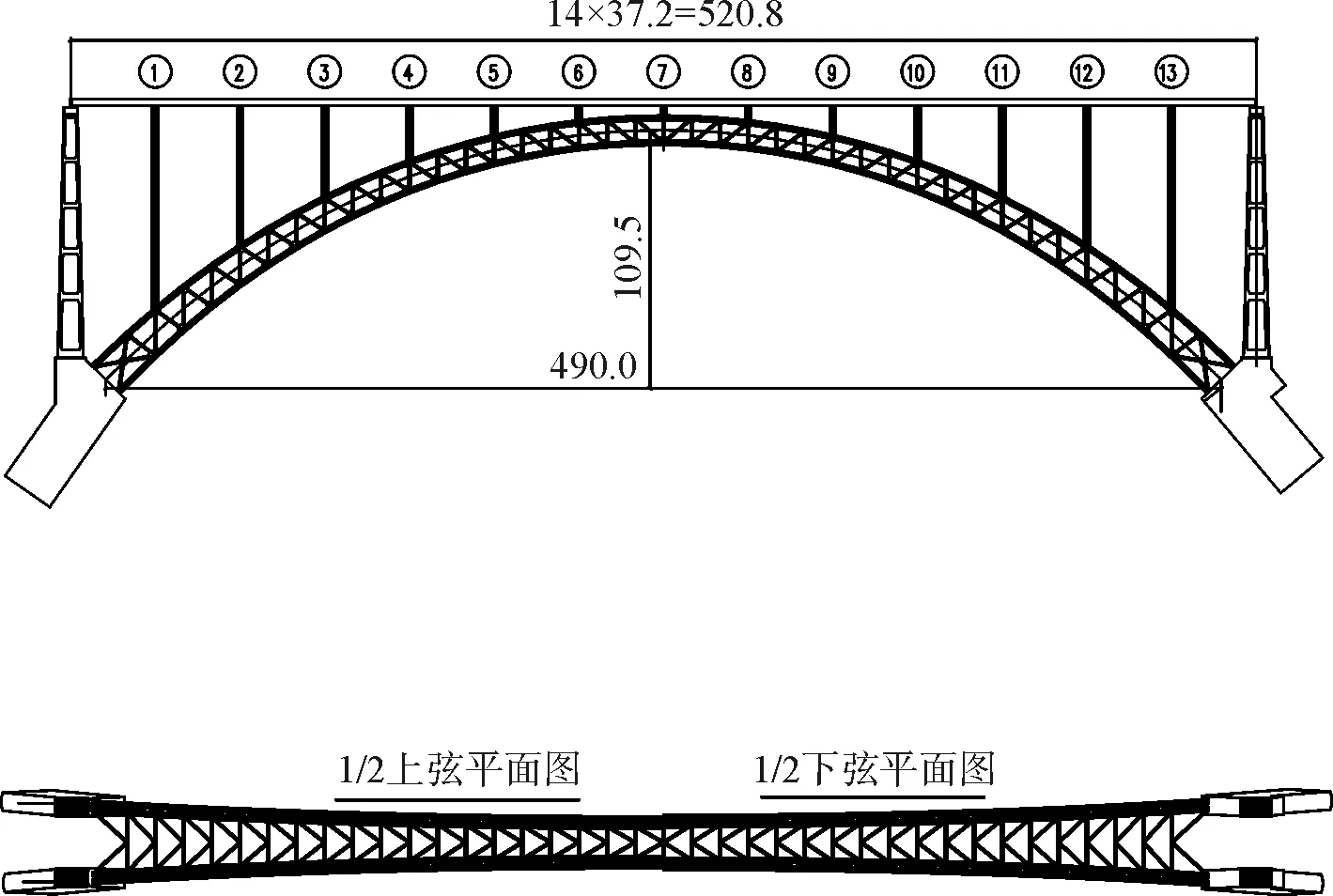
图1 结构简图
1.2 有限元模型
使用空间有限元分析软件Midas/Civil建立全桥三维有限元模型。共采用2个结构模型,模型1为最大悬臂施工阶段,模型2为主拱合龙施工阶段,以探讨桥梁在施工阶段的抗震性能,并评估主拱合龙对桥梁抗震性能的影响。
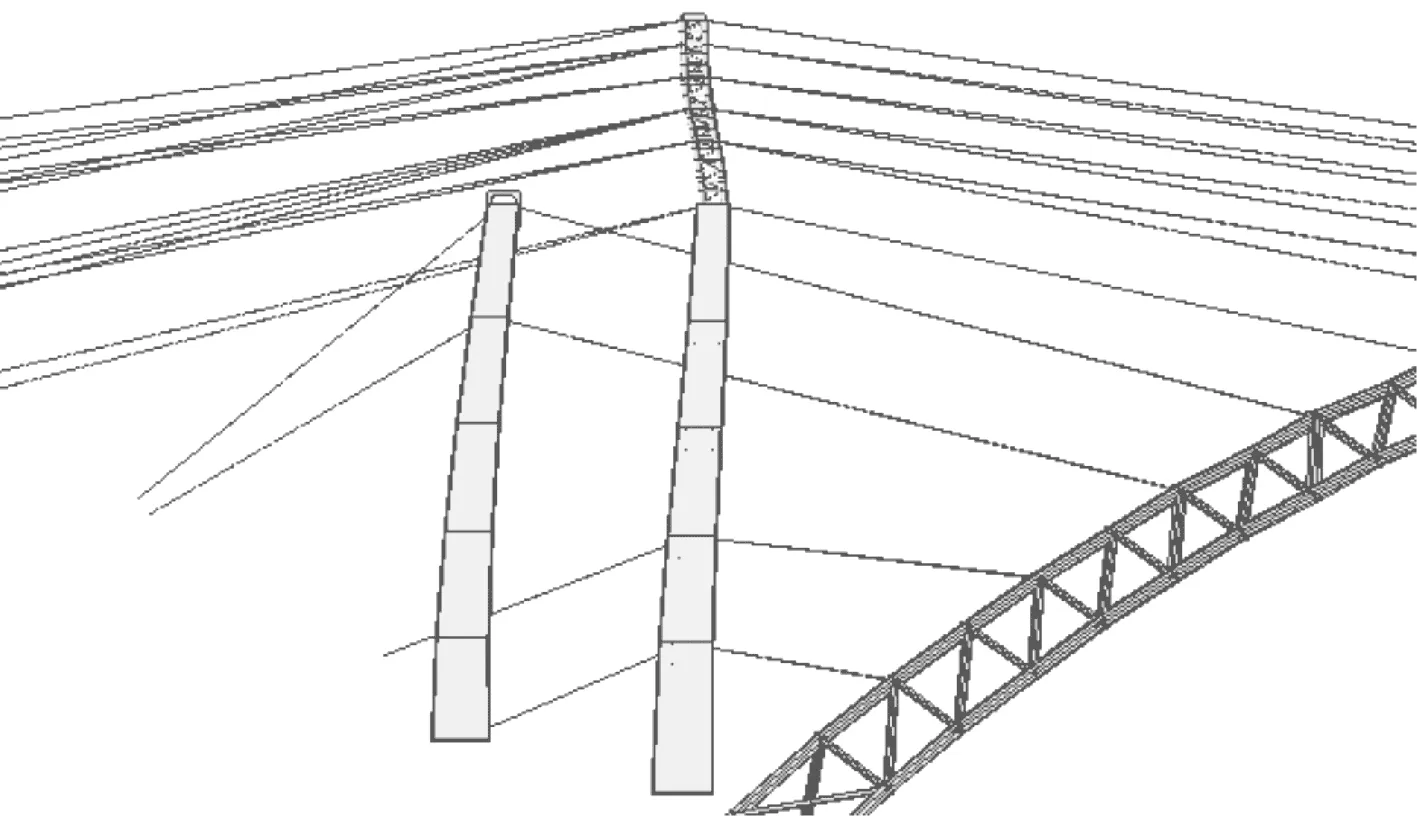
桥梁拱圈、交界墩、扣塔采用梁单元模拟,扣锚索采用只受拉桁架单元模拟;拱圈采用Q370qE及Q345q,交界墩采用C35,扣塔采用Q345q;交界墩墩底采用固结连接形式,扣锚索锚碇边界条件为固结,立柱与主拱采用刚性连接;阻尼按照规范设为0.03。计算模型见图2。
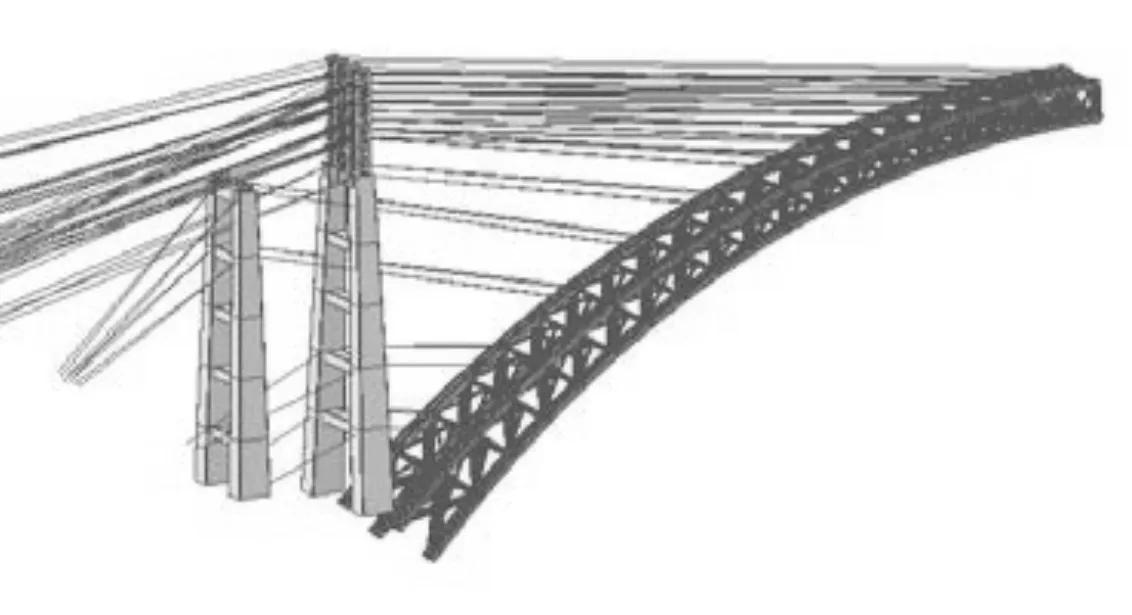
(a) 最大悬臂
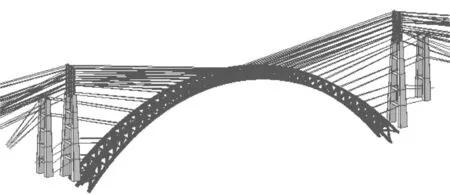
(b) 拱圈合龙图2 有限元模型
1.3 地震激励
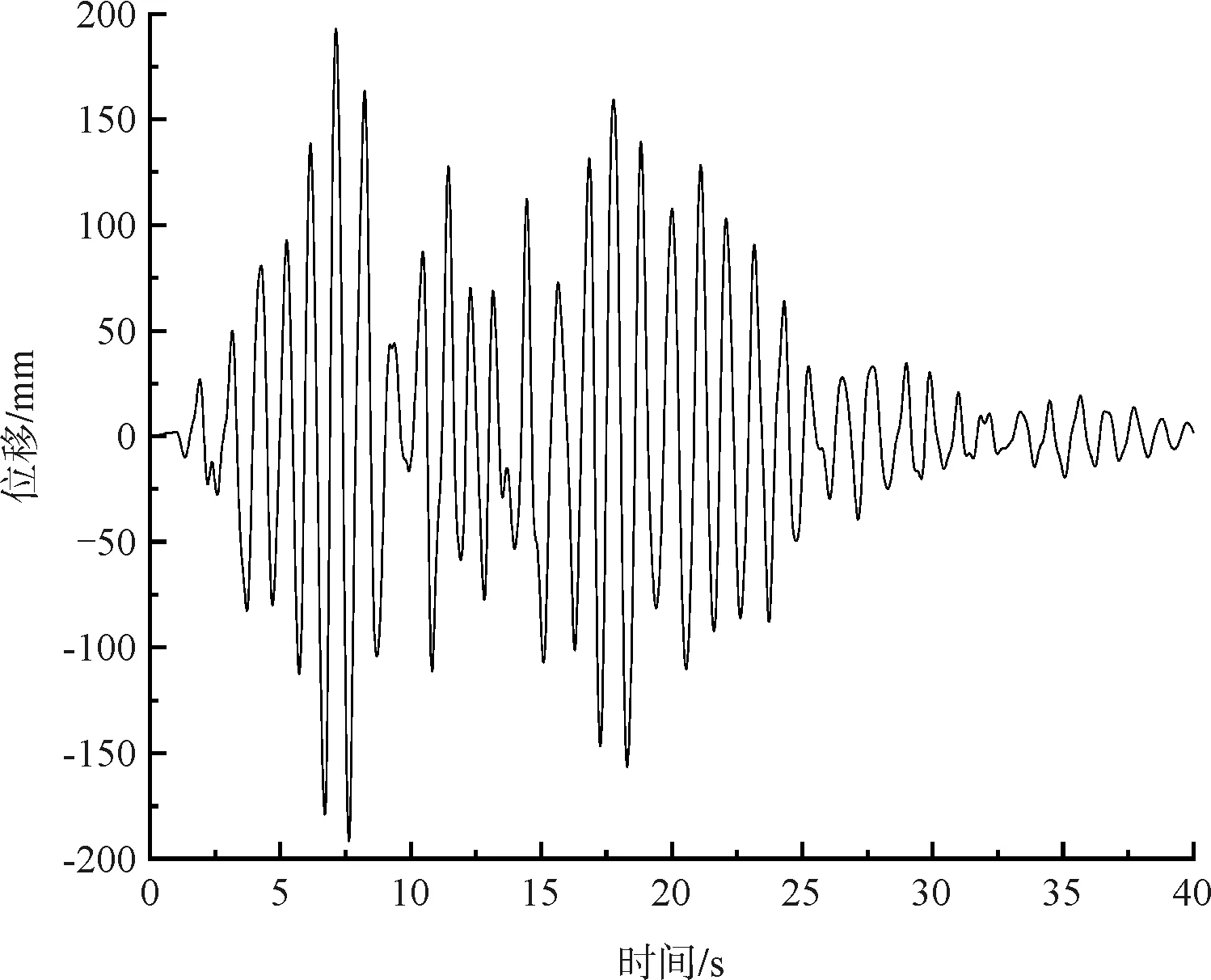
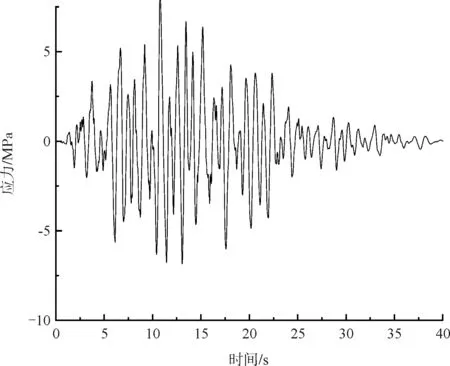
采用时程分析法对施工阶段桥梁的抗震性能进行分析。该桥是位于地震烈度Ⅷ度区的A类工程,桥址所在场地的工程地震条件进行过专门研究,本文选用三条基于场地安全评估报告的罕遇地震波(50年超越概率2 %)(图3)作为输入,地震波加速度峰值为0. 42g,持时40s。同时参考规范[9],竖直方向地震激励按水平方向地震动的65 %进行分析。参考欧洲规范,分别按照以纵向地震力为主、横向地震力为主、竖向地震力为主,选取以下荷载组合方式:
荷载组合Ⅰ:100 %纵向绝对值+30 %横向绝对值+30 %竖向绝对值。
荷载组合Ⅱ:30 %纵向绝对值+100 %横向绝对值+30 %竖向绝对值。
荷载组合Ⅲ:30 %纵向绝对值+30 %横向绝对值+100 %竖向绝对值。

图3 罕遇地震地震波
2 计算结果
2.1 自振特性分析
动力特性分析是进行抗震分析的基础,本文计算结构前30阶振型,保证结构在三个方向振型参与质量在90 %以上,两施工阶段前5阶振型计算结果如表1、表2所示。
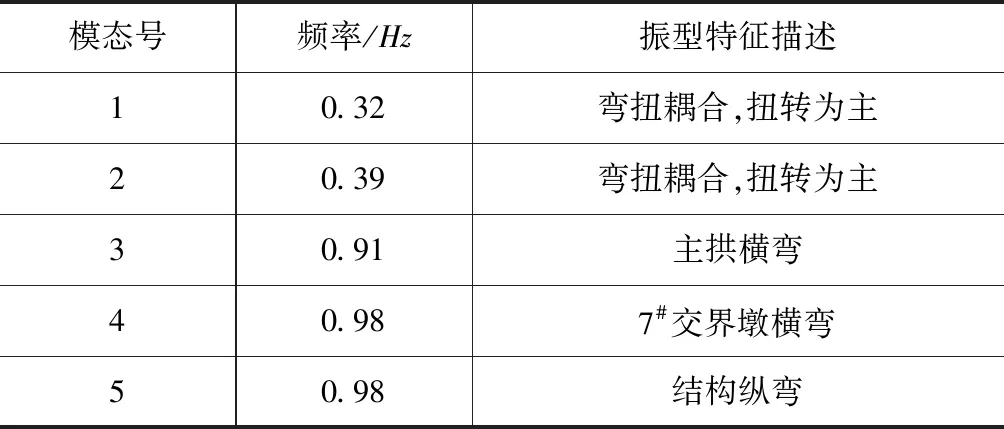
表1 悬臂施工阶段结构自振特性
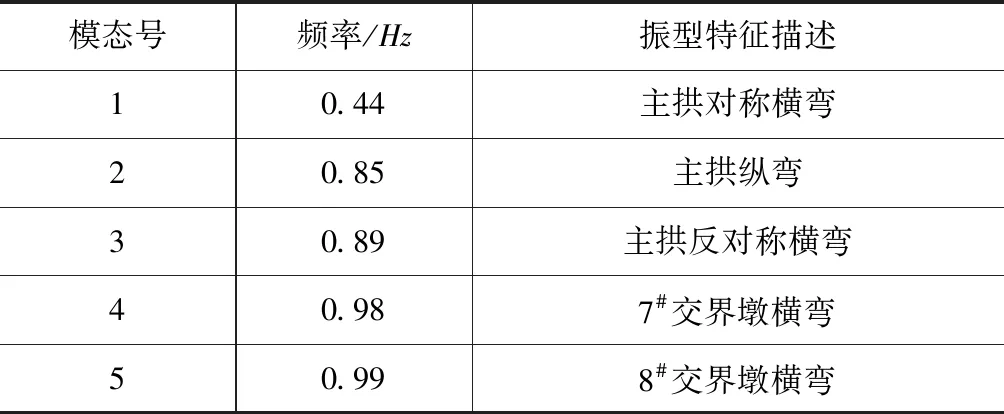
表2 拱圈合龙阶段结构自振特性
计算结果显示:在最大悬臂阶段,结构的第1阶振型为主拱竖向扭转,频率为0.32Hz,前两阶振型主要都是结构扭转,扭转与横弯出现频率较高;在主拱合龙后,结构的第1阶振型为主拱对称横弯,频率为0.44Hz,第2阶振型为主拱纵弯,横向弯曲出现频率较高。分析可知,结构振型中横向振动发生频率较高,且分布在前期模态中,说明结构横向刚度较低,施工期间需注重横向抗震性能设计。
主拱合龙后,结构低阶频率显著增高,基频增大37.5 %,说明主拱合龙能够显著增强结构刚度;通过对振型特征分析可知,主拱合龙后,低阶振型中不再出现结构扭转,但是横向振动出现频率仍较高,说明主拱合龙能够增强结构抗扭刚度,但横向刚度并无显著变化。
2.2 地震响应结果分析
针对研究内容,本文对2个模型进行计算分析,并给出施工阶段桥梁的上、下弦杆、扣塔在各工况下的内力变化图。扣塔是重要的临时结构,因此本文同时给出扣塔底端、顶端节点在最不利地震作用为主的荷载作用下的位移时程曲线。
2.2.1 最大悬臂施工阶段
最大悬臂施工阶段地震作用计算结果见图4、图5、图6所示。由计算结果可知:
(1)上弦杆、下弦杆、扣塔的最大应力分别为133MPa、-128MPa、145MPa,均满足材料屈服强度要求,上弦杆最大拉应力出现在1/4跨附近,下弦杆最大压应力在1/4跨附近,扣塔最大应力出现在塔底。
(2)地震作用会大幅增加弦杆应力,上弦杆的增量相对明显,在荷载组合Ⅰ作用下最大增幅达到103MPa。
(3)不同地震荷载组合作用,上、下弦杆与扣塔的应力分布规律基本一致。悬臂阶段桥梁在纵向地震作用为主的荷载作用下有最大应力响应,扣塔的响应最为明显,这是因为扣塔通过扣索与主拱弦杆连接,其应力变化与弦杆应力变化保持一致。
(4)在荷载组合Ⅰ作用下,扣塔顶端最大纵向位移66.4mm,底端最大纵向位移165mm。由图5可见,13.4s时,扣塔顶端与底端纵向位移差最大为131.8mm,主要是由于塔墩固结,而桥墩上部半部分无扣锚索约束,导致墩顶纵向位移比塔顶位移还要大(图6)。在荷载组合Ⅱ作用下,扣塔顶端最大横向位移205.1mm,底端最大横向位移192.9mm,由图5可见,地震作用过程中扣塔顶端、底端横向位移变化规律保持一致。
(5)交界墩底部在荷载组合Ⅰ作用下墩身最大拉应力为-6.6MPa,超过规范规定的C35混凝土极限抗拉强度2.25MPa,交界墩存在较大破坏风险。
2.2.2 主拱合龙阶段
主拱合龙后,地震作用下计算结果见图7、图8所示。由计算结果可知:
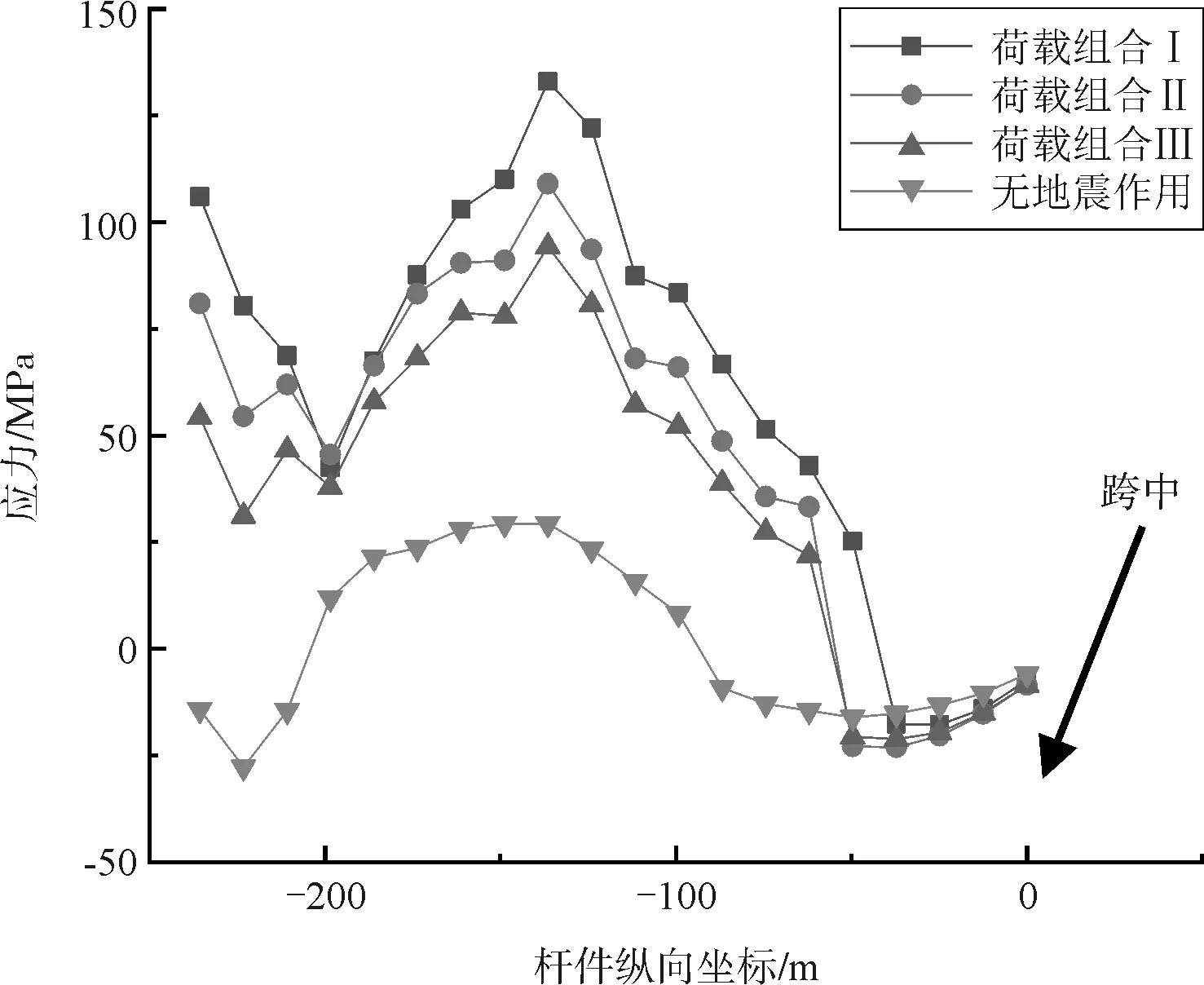
(1)上弦杆、下弦杆、扣塔的最大应力分别为119MPa、-153MPa、180MPa,均满足材料屈服强度要求。上弦杆最大应力出现在1/4跨附近,下弦杆最大应力出现在拱顶,扣塔最大应力出现在塔底。
(2)地震作用会大幅增加弦杆应力,上弦杆的增量相对明显,在荷载组合Ⅰ作用下杆件最大增幅达到85.2MPa。
(a) 上弦杆应力
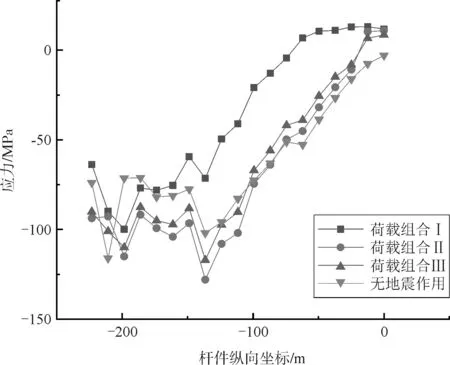
(b)下弦杆应力
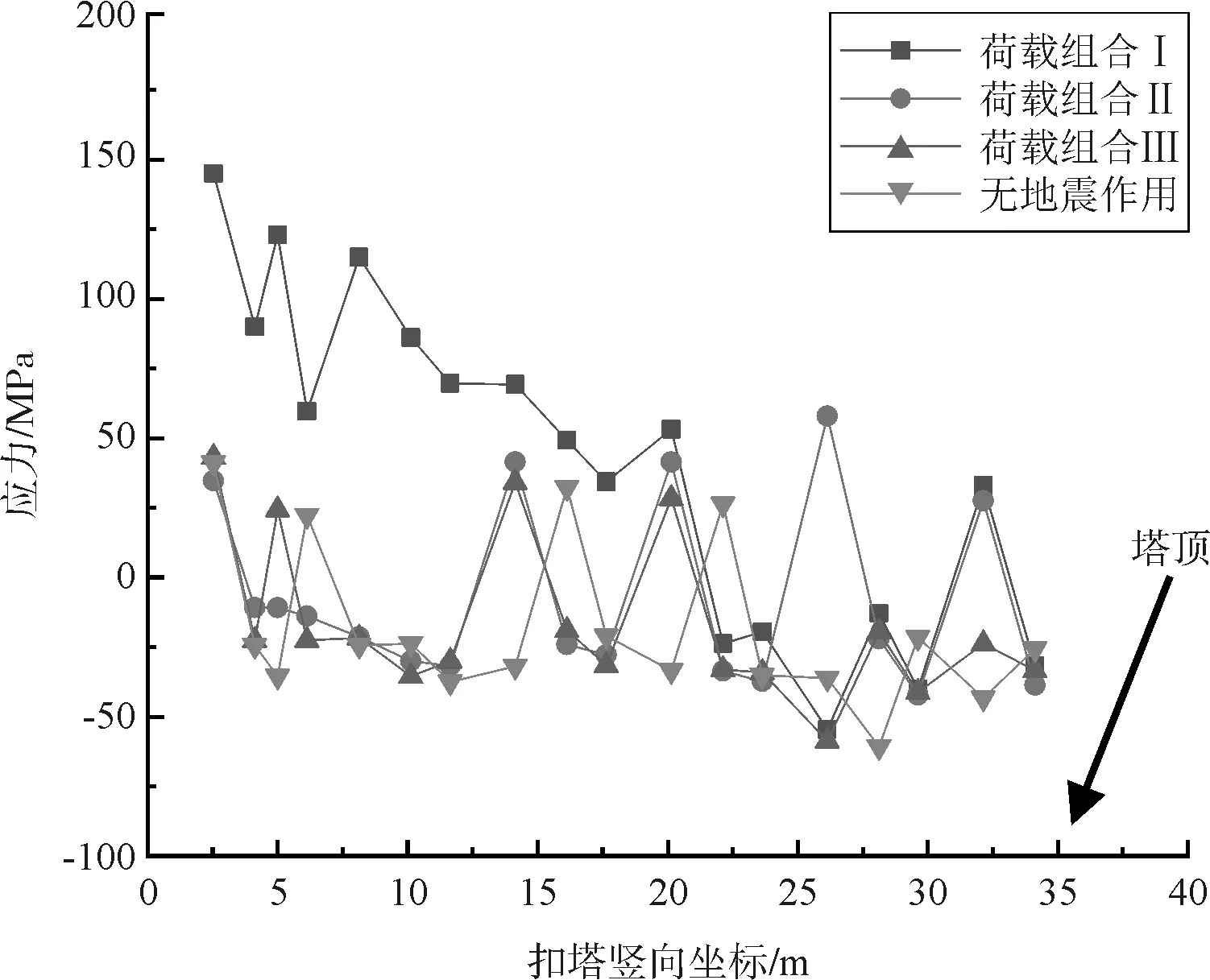
(c)扣塔应力
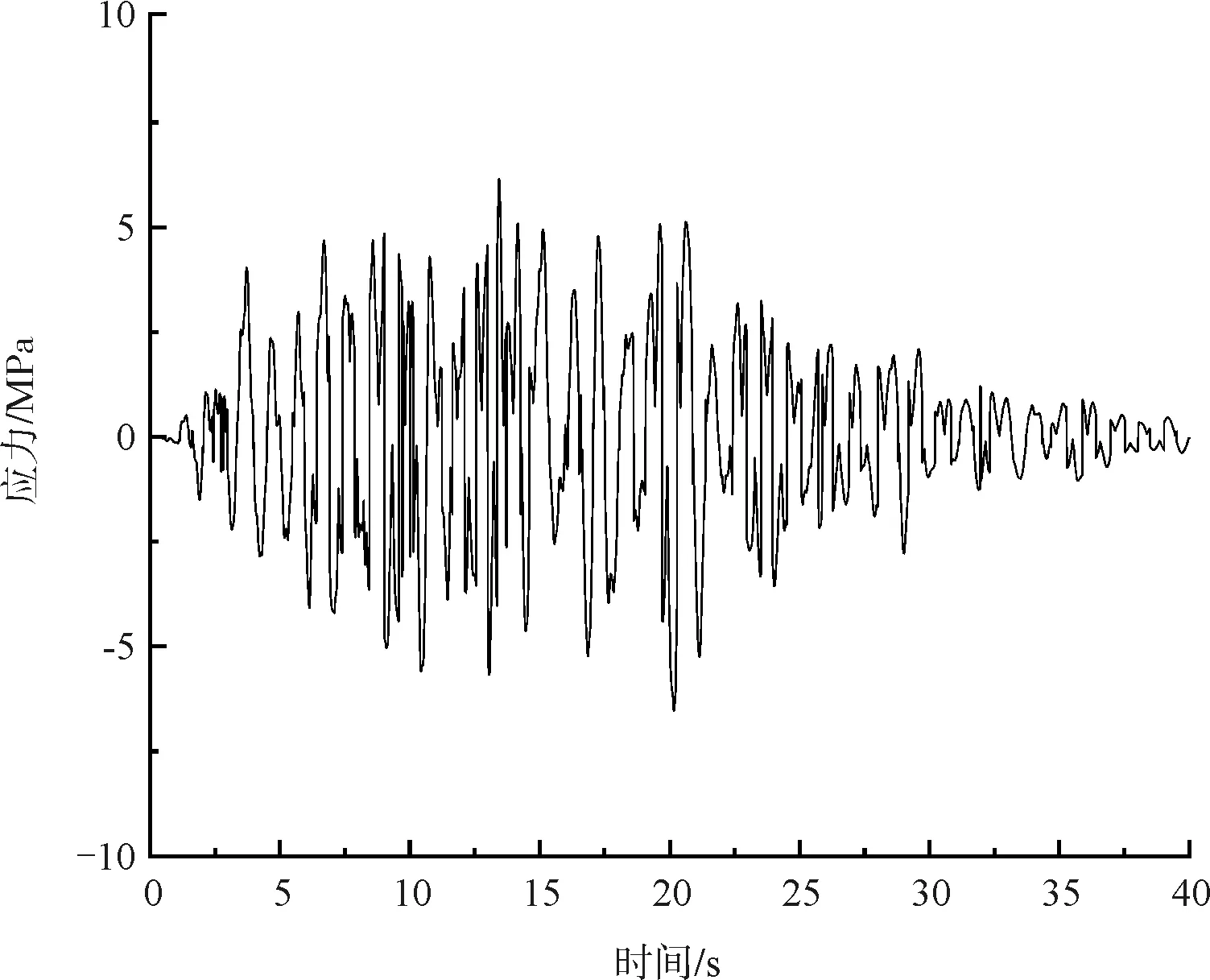
(d)荷载组合Ⅰ作用交界墩底部应力时程
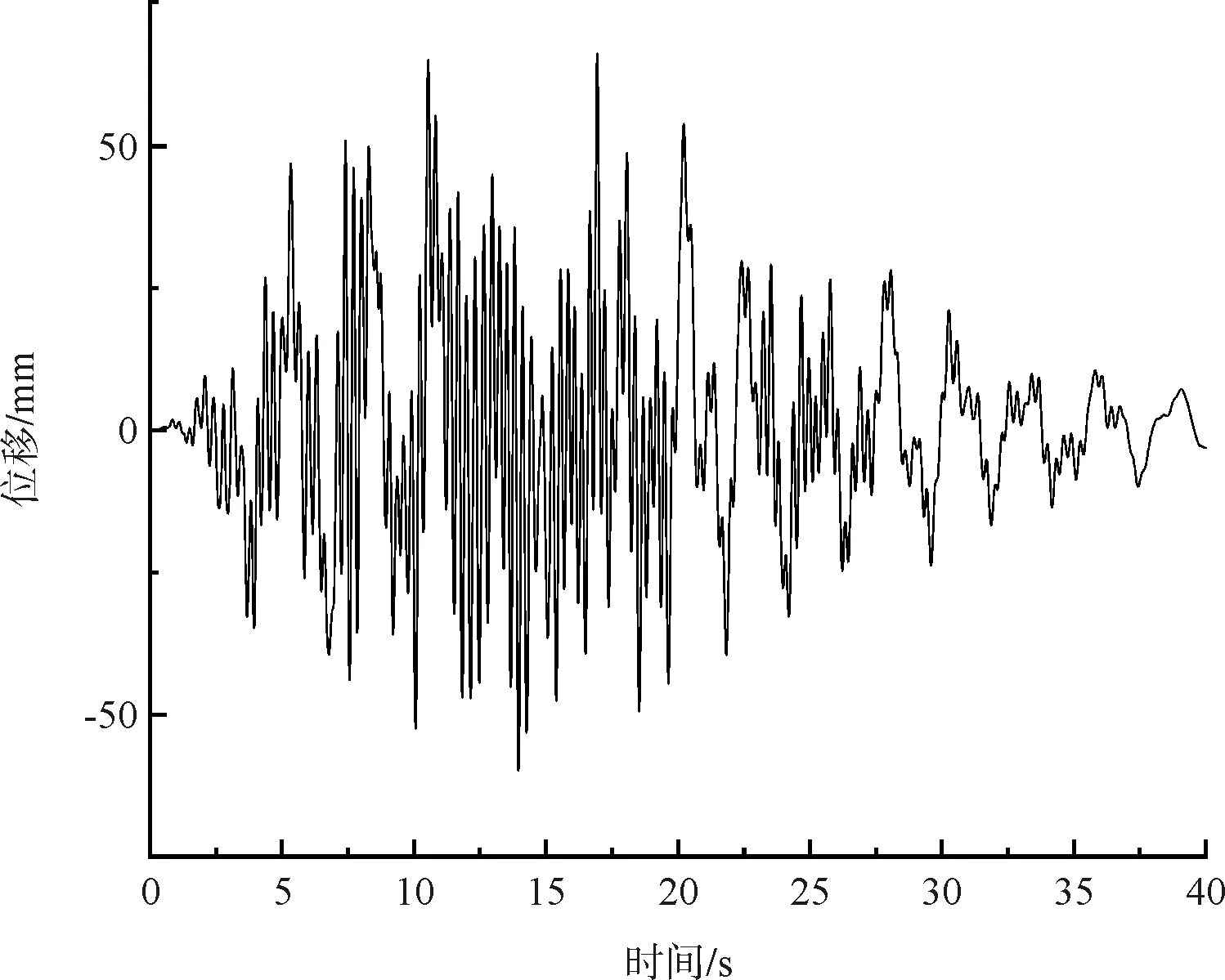
(a)荷载组合Ⅰ作用扣塔顶端X方向时程
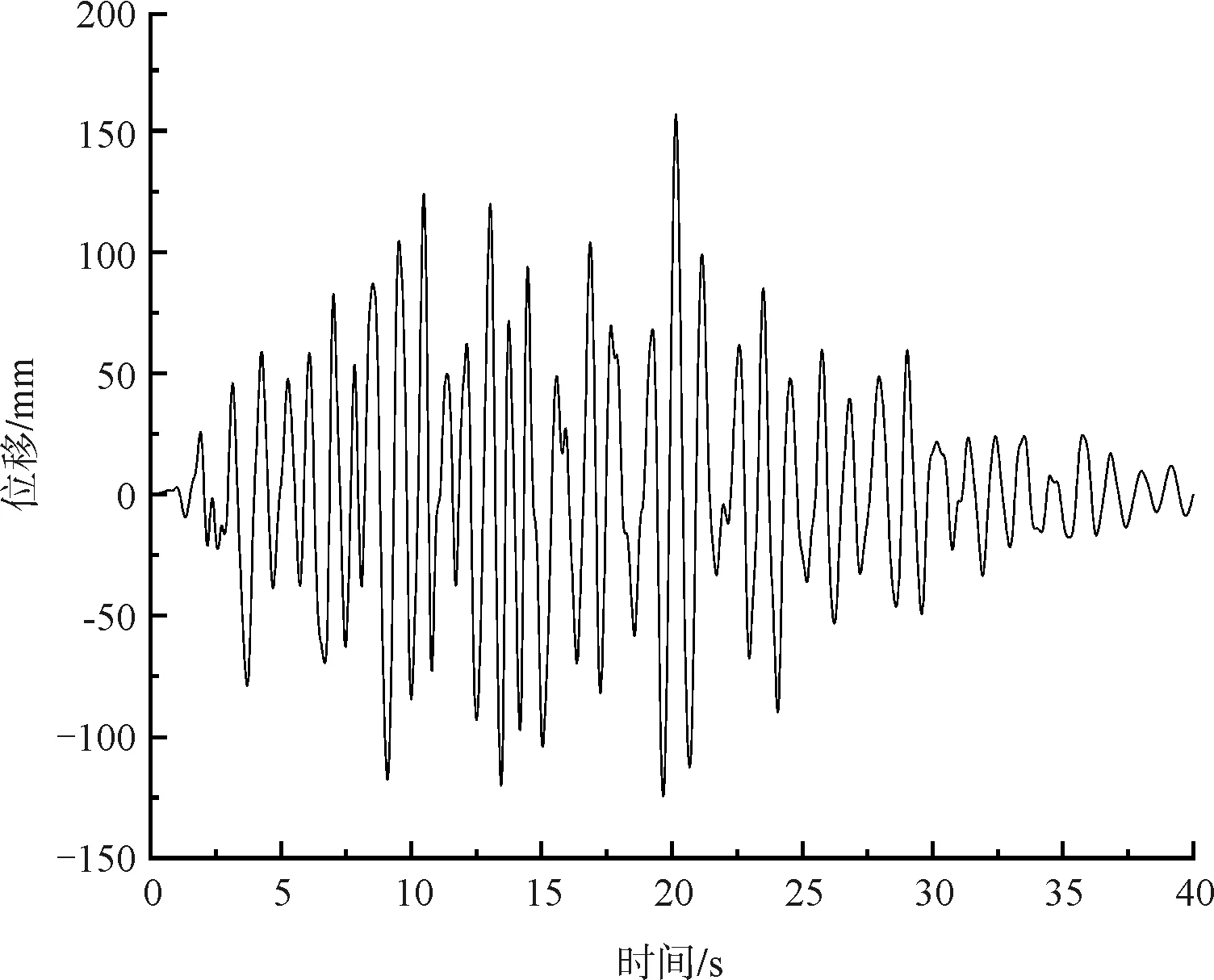
(b)荷载组合Ⅰ作用扣塔底端X方向时程
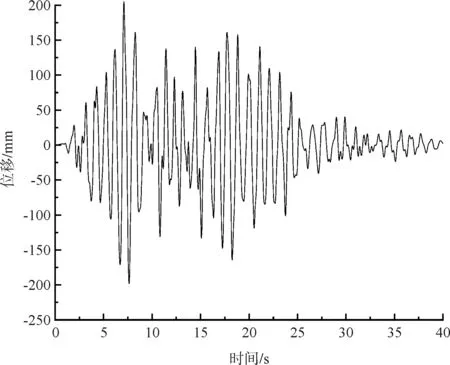
(c)荷载组合Ⅱ作用扣塔顶端Y方向时程
(d)荷载组合Ⅱ作用扣塔底端Y方向时程
(a)荷载组合Ⅰ作用X方向变形示意
(b)荷载组合Ⅱ作用Y方向变形示意图6 扣塔、交界墩位移
(3)不同荷载组合作用,上、下弦杆与扣塔的应力分布规律基本一致。上、下弦杆在纵向地震作用为主的荷载作用下内力变化最大,扣塔在横向地震作用为主的荷载组合下应力变化最大,可见合龙能够改善桥梁主体结构的纵向抗震性能,但扣塔的抗震性能无显著改变。
(4)在荷载组合Ⅰ作用下,扣塔顶端最大纵向位移109.2mm,底端最大纵向位移192.3mm。由图5可见,13.4s时,扣塔顶端与底端纵向位移差最大为131.8mm;在荷载组合Ⅱ作用下,扣塔顶端最大横向位移205.1mm,底端最大横向位移192.9mm。 位移变化规律与最大悬臂阶段相似。
(5)相比于最大悬臂阶段,相同荷载作用下上弦杆应力部分降低,下弦杆应力增加,说明结构整体受力更加合理。这是由于主拱合龙后改善了结构内部的刚度分配,使得地震力能够更加均匀的分配给所有杆件承担。
(6)相比于最大悬臂阶段,扣塔的纵向位移明显降低。这是由于主拱合龙后,结构的纵向刚度显著增加,纵向变形大幅下降,从而减少对扣塔位移的影响。
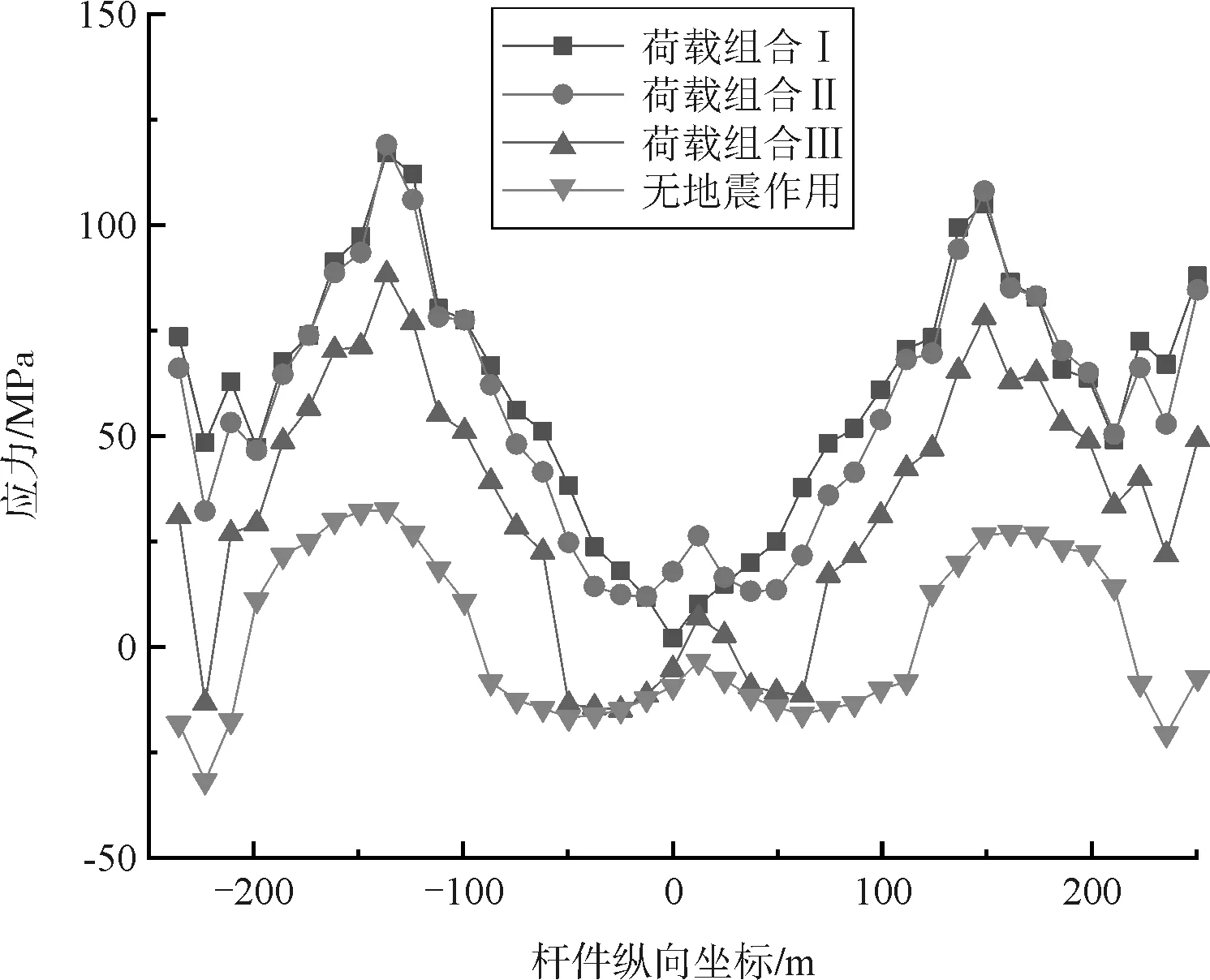
(a)上弦杆应力
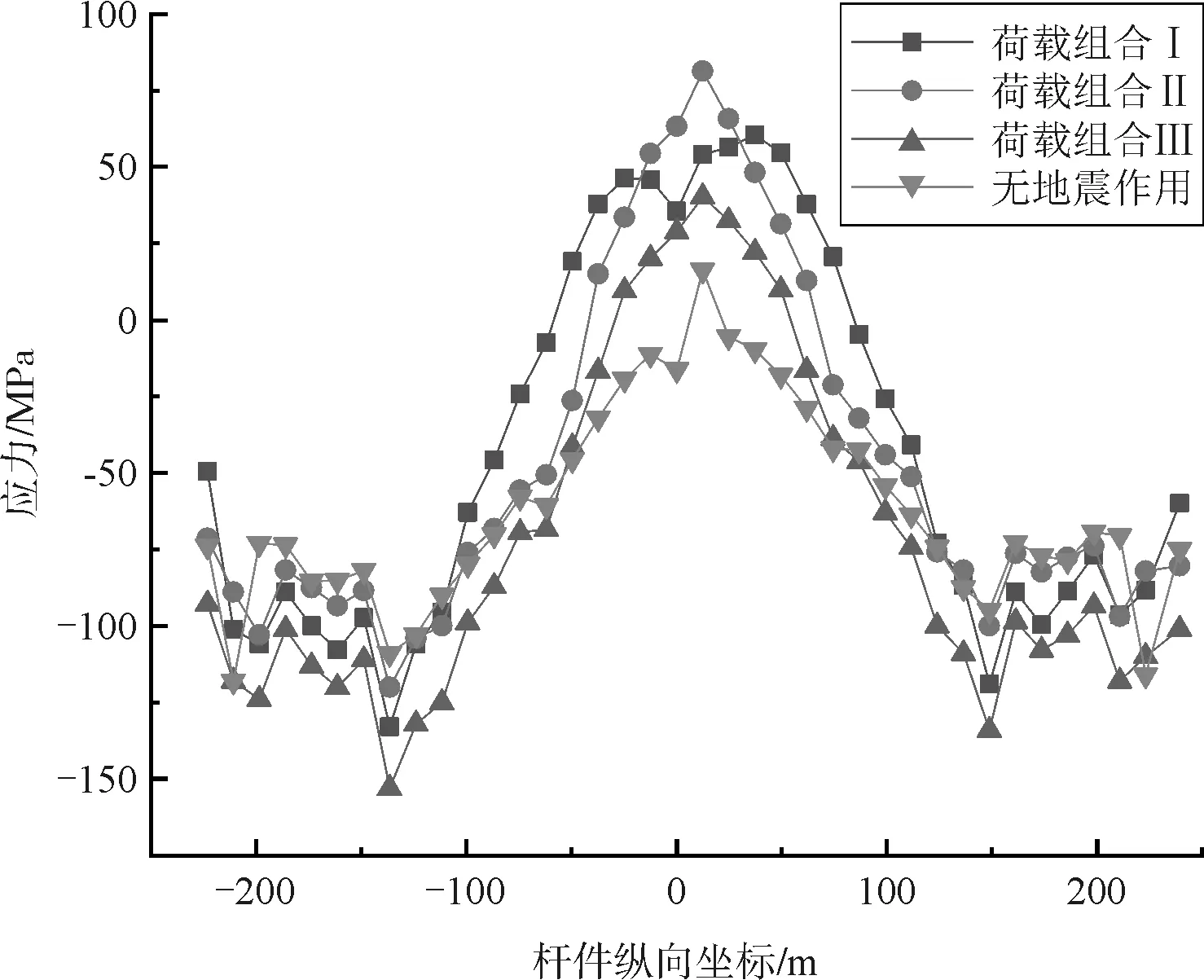
(b)下弦杆应力
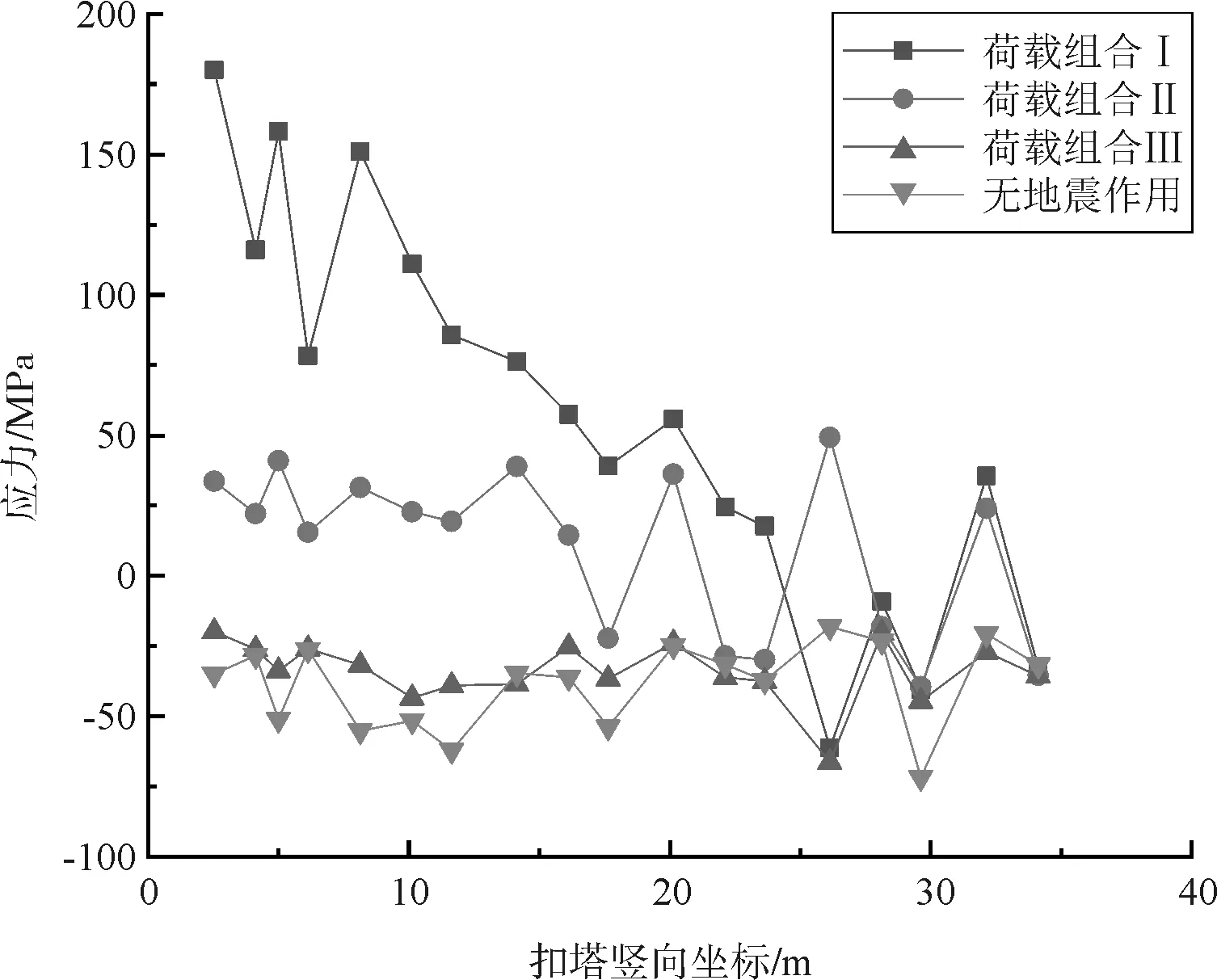
(c)扣塔应力
(d) 荷载组合Ⅰ作用交界墩底部应力时程
3 结 论
(1)悬臂施工状态的桥梁扭转刚度、横向刚度均较弱,扭转对低阶振型的贡献率较高,结构易发生扭转变形;主拱圈合龙阶段的桥梁横向刚度相对较弱;合龙能够大幅改善结构的抗扭能力。
(2)处于最大悬臂施工阶段和主拱圈合龙阶段的桥梁在罕遇地震作用下,主要构件材料未达到屈服强度,但扣塔在横向地震作用下发生较大的横向位移,建议在设置横向缆风索,以增加横向稳定性。
(3)扣塔在水平地震作用下的应力响应与位移响应均较为明显,比弦杆更剧烈。在纵向地震力作用下,扣塔的应力响应突出;横向地震力的作用下,扣塔的位移响应突出。考虑到施工过程中,实际扣锚索比理论扣锚索索力更大,可能导致扣塔的恒载异地力更大,在地震荷载作用下风险增大,鉴于此建议对扣搭下部杆件予以加强设计。
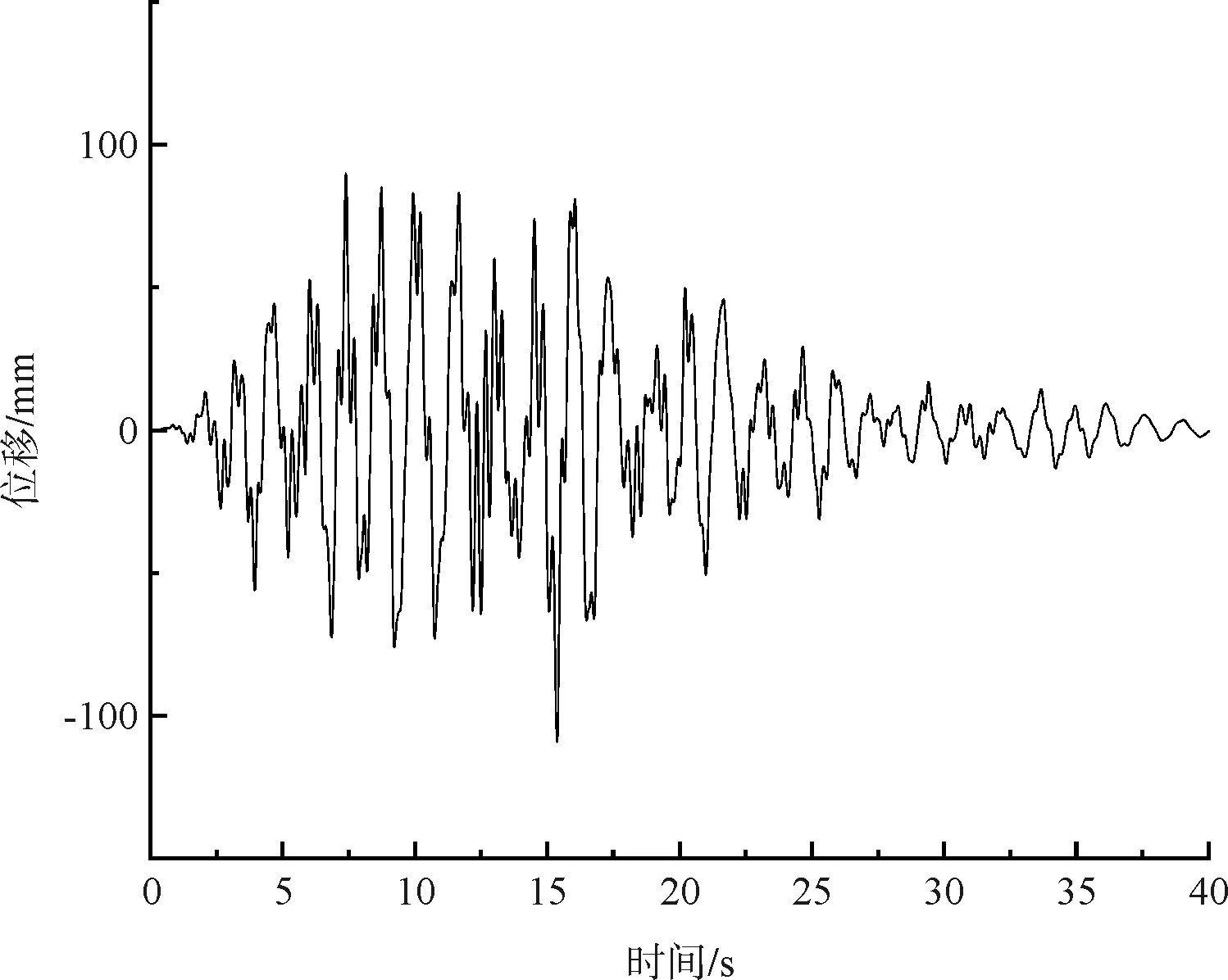
(a)扣塔顶端X方向时程
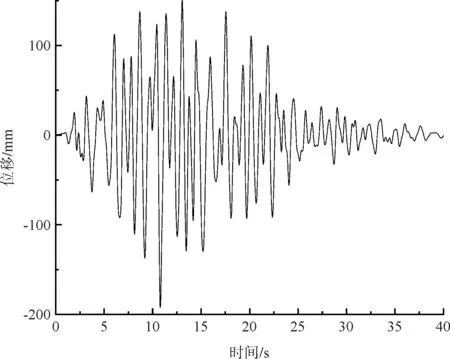
(b)扣塔底端X方向时程
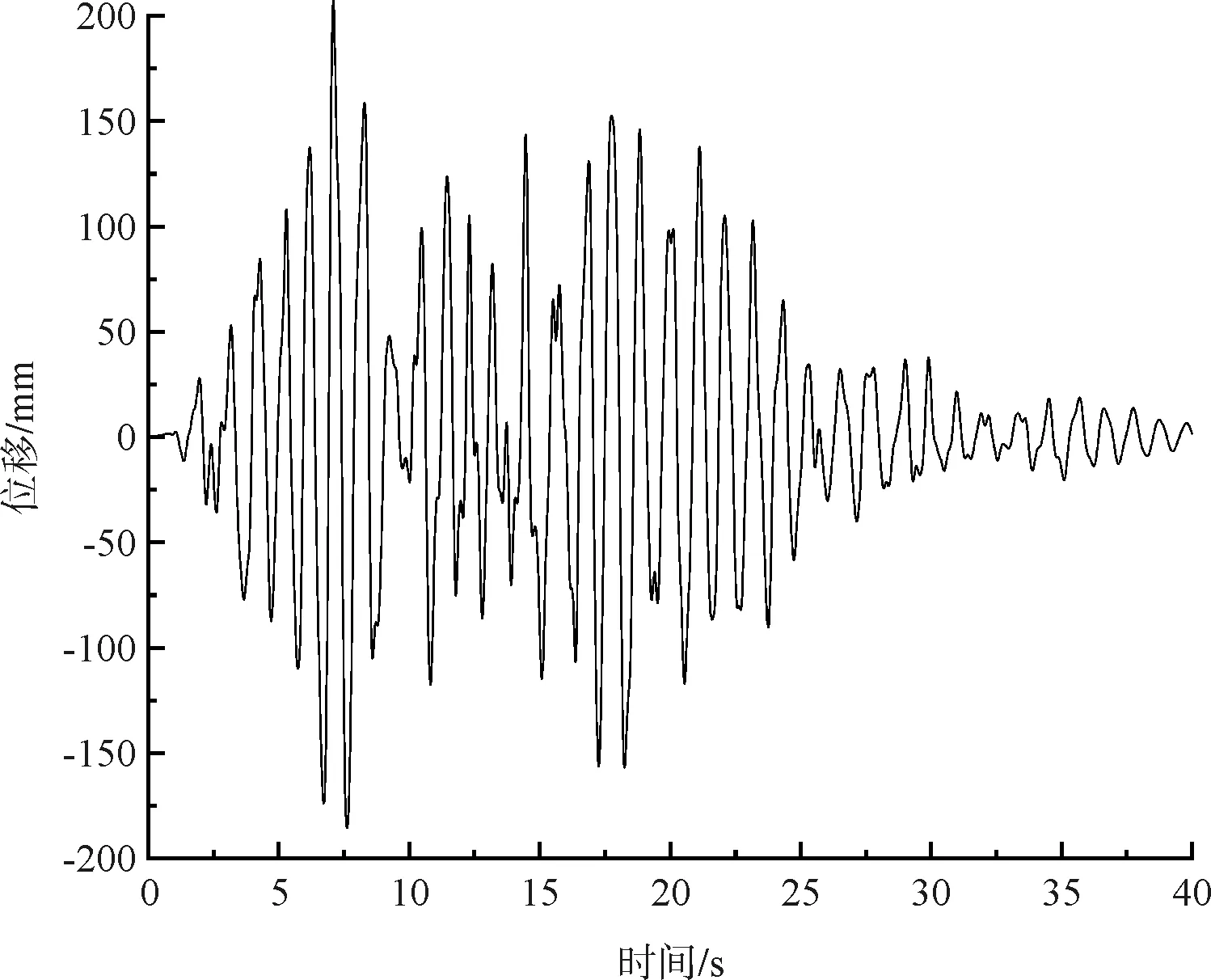
(c)扣塔顶端Y方向时程
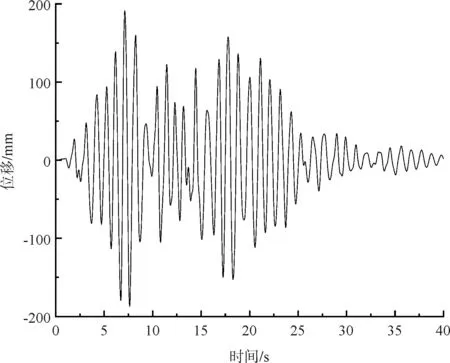
(d)扣塔底端Y方向时程
(4)主拱合龙能够改善结构内部刚度分配,使得结构在地震作用下的受力偏向均匀;同时合龙能明显提高主体结构的纵向抗震性能,从而部分改善扣塔的纵向抗震性能。
