基于Benders分解的煤炭供应链网络维护调度优化

高吉冰，郑澜波

(武汉理工大学 物流工程学院，湖北 武汉 430063)

煤炭行业作为我国国民经济的重要支柱，每年我国有数十亿吨的煤炭消费总量，但大部分煤炭都不是本地直接消费的，而是经过长途运输才能从生产地到达使用地，整个运输过程涉及到煤矿、铁路、船公司、港口和煤炭用户等众多企业。这些企业之间相互协作，构成了一个庞大的煤炭供应链网络。煤炭供应链网络的作业设备必须经常进行预防性维护，但传统的人工调度方法效率低、可处理时间区间有限，已不能满足当下的需求，于是作业设备预防性维护时如何更加科学有效地调度成为当下煤炭供应链亟需解决的问题。BOLAND等[1]提出的带边中断动态网络最大流问题为解决此问题提供了新的研究方向，首次提出使用网络流的理论来解决维护调度问题。

目前对设备维护的定量研究，主要集中在制造业生产研究，很少涉及煤炭供应链。VATN等[2]提出了一种确定生产系统部件最优维修计划的方法，将安全健康环境目标、维修费用和损失生产成本考虑在内，对多个目标进行了优化。叶培钒[3]基于状态维修策略研究了针对系统维修的优化问题。李有堂等[4]考虑多设备混联系统，提出了一种以作业计划为约束的动态维护策略模型。SOUSA等[5]提出了一种选择和确定关键设备维修任务的方法，并将该方法应用于案例工厂，取得了不错的效果。门峰等[6]为了有效降低汽车质保期内制造商的维修成本，提出了基于汽车固定使用里程的预防性维修方法，能有效降低汽车的整体维修成本。

针对煤炭供应链网络设计的研究，CONRADIE等[7]研究了煤炭的开采、堆垛和回收的作业调度问题，提出的模拟退火算法在求解大规模实例问题时取得了不错的效果。PENG等[8]将原煤的生产、洗选、加工、运输、销售整合为一个模型进行分析，并将其应用于煤矿生产。范志强[9-10]加入新的配煤加工和流量平衡等约束，构建了煤炭供应链网络混合整数规划模型，此后又针对复杂产品需求特性，在以上基础上规划了新的四级煤炭供应链网络模型，并设计了遗传算法进行求解。袁旭梅等[11]考虑整个煤炭供应链，以煤矿、铁路装载点、港口和煤炭消费客户构成的海运煤炭供应链为研究对象，提出了考虑港口物流能力的供应链网络优化问题。

目前的研究倾向于合理规划整个煤炭供应链网络，并未考虑维护问题，且相对于普通制造业供应链，煤炭行业供应链涉及的流通环节和相关企业多，运输过程复杂，对整个煤炭供应链进行优化尤其困难，所以制造业的维护模型很难适用于煤炭供应链。因此，BOLAND等针对猎人谷煤炭供应链网络设计问题，抽象出带边中断动态网络最大流问题，设计了贪婪启发式算法对问题进行求解。由于该网络设计问题为NP-hard问题，具有调度和网络流相结合的特性，因此使用Benders分解求解十分有效。刘茜[12]设计了一种基于重复求解主问题的Benders分解算法(classical benders decomposition,CBD)，研究显示与Gurobi相比，CBD算法求解此类问题十分有效。PEARCE等[13]则设计了一种基于分支定界树的Benders分解算法(branch and benders cut,B&BC)，发现与Boland相比，B&BC算法求得最优解的算例大幅提升。虽然上述两位学者使用了CBD算法和B&BC算法对问题求解，但无论是算法的结构还是终止条件，以及对于求解结果的处理均存在诸多不同，因此无法进行有效比较。B&BC算法作为近几年才流行起来的Benders分解，其在求解器分支定界过程加入Benders cut的思路为Benders分解提供了一种新的研究方向。目前国内外很少有文献针对CBD算法和B&BC算法的求解优劣进行对比，因此从煤炭供应链网络维护调度的角度探讨两种算法各自适合应用的工业问题规模是很有必要的。

笔者从整个煤炭供应链设备维护的运营角度出发，描述带边中断动态网络最大流问题的构建过程，基于问题特殊的网络流和调度特征，分别设计CBD和B&BC两种Benders分解算法，并针对这两种算法在不同规模算例下的求解效率进行对比分析。其中，对于B&BC算法，从子问题和主问题两个方向，分别使用预流推进算法、加入有效不等式的方式对算法进行了改进，以使得问题的求解效率得到提升。

1 问题描述及模型

1.1 问题描述

煤炭在矿山被开采出来经过铁路的运输到达港口，在港口经过翻车机、堆料机、取料机、装船机等轮番作业后到达船舶。无论铁路还是港口，都对应着多条煤炭运输线路，这些线路互相连接形成了一个庞大的煤炭供应链网络，如图1所示。其中，有向箭头表示煤炭在铁路和港口各设备间的流动方向。每个设备都有固定的单位时间处理能力，且设备都要定期进行预防性维护。对于每一个维护工作，都存在最早开始时间、最迟截止时间和处理时间，且维护工作一旦开始就必须完成。因此当同时出现多个维护工作时，合理调度这些维护工作对于保障整个网络的高效运行就变得至关重要。

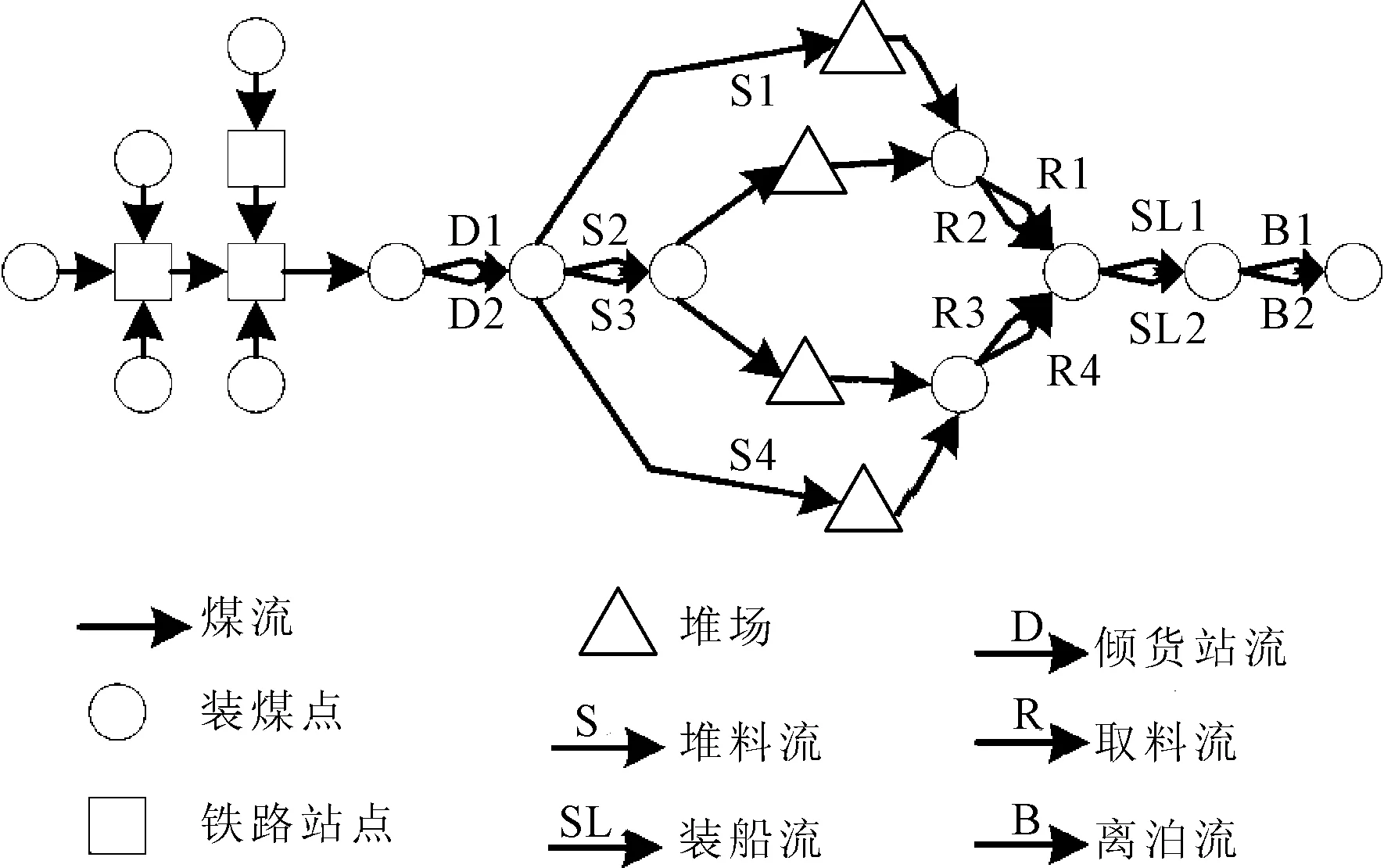
图1 煤炭供应链网络

由于煤炭供应链网络具有环节多、结构复杂、动态变化的特点，普通的数学模型难以精确描述整个问题，而网络流模型具有灵活、可扩展性强的特性，非常适合刻画煤炭供应链网络。建模时，铁路网和码头装卸、运输设备网的组合被表示为一个数学网络G=(V,A)，煤炭则被表示为流经网络中弧的流，每条弧对应一定的容量，表示设备单位时间的处理能力。在这个网络中，如果设备停止运行进行维护工作，则代表弧中断即容量为零，此时煤炭无法流经此弧。

1.2 参数设置

定义网络G=(V,A)，V为网络中节点的集合，s为源点，s′为汇点，A为网络中弧的集合；离散时间变量t∈[T]={1,2,…,T}，[k,l]={k,k+1,…,l}；Ca为每一条弧a∈A对应的容量；δ+(v)为流出每一个节点v∈V的弧集；δ-(v)为流入每一个节点v∈V的弧集；J为所有维护工作的集合；Ja为弧a上维护工作的集合；pj∈Ν为每一个维护工作j∈J的处理时间；rj∈[T]为每一个维护工作j∈J的最早开始时间；dj∈[T]为每一个维护工作j∈J的最迟截止时间；若给定一个调度计划，弧a维护工作开始时间为sj(j∈Ja)，那么弧a在t∈[sj,sj+pj-1]内流量为0。

1.3 数学模型

(1)决策变量：φat∈R+表示时间t上流经弧a的流量,a∈A,t∈[T]；xat={0,1}，若时间t上弧a是连通的，则xat的取值为1，否则为0；yjt={0,1}，若维护工作在j时间开始，则yjt的取值为1，否则为0,j∈J,t∈[rj,dj-pj+1]。

(2)目标函数：

(1)

s.t.

∑dj-pj+1t=rjyjt=1，j∈J

(4)

(5)

目标函数式(1)表示最大化时间T内整个网络的流量；约束条件式(2)保证了每一个节点的流量守恒；约束条件式(3)确保每一条弧的流量都不超过弧的容量；约束条件式(4)要求每项维护工作在规定时间窗内被维护一次；约束条件式(5)保证了当维护工作在时间t进行时，弧a是中断的，且弧上的流量为0。

式(2)和式(3)组成了一个网络最大流问题，准确描述了整个煤炭供应链网络的结构；式(4)和式(5)描述了一个调度问题，将决定维护工作所有的计划方案。两个问题通过弧中断变量xat连接，即调度问题将维护计划通过xat传递给网络最大流问题完成整个问题的求解。

2 Benders分解算法设计

2.1 Benders模型分解设计

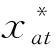
(6)

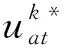
2.2 CBD与B&BC算法设计

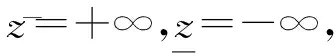
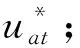
与CBD重复求解主问题不同，B&BC算法只需求解一次主问题，利用求解器的callback函数在分支定界框架下对其中可行的分支节点进行探索，从而产生Benders cut。在B&BC算法中，Benders cut是以松弛约束的形式加入模型，这种约束的优点是只有当这种约束被违反时才会被加入模型，但是这种约束会使得模型在一开始的预求解阶段对于模型的缩减变得十分小心。

2.3 融合预流推进算法

由于Benders分解算法的求解效率主要受到主问题和子问题求解效率的影响，因此针对主问题和子问题特殊的结构进行改进是加快求解的一种有效方式。带边中断动态网络最大流问题的子问题是一个网络流问题，传统的Gurobi建模默认使用单纯形法对子问题进行求解，并未有效利用子问题的结构。

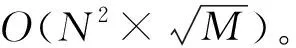
2.4 加入有效不等式

虽然改进子问题的求解算法在理论上能加快问题的求解速度，但是经过研究证实，主问题在整个求解过程占时能够达到90%,甚至更多。因此,从优化的角度来看，改进主问题的求解将是提升求解效率的一个更加有效的方法。

由于经过映射和松弛以后，主问题已经没有子问题的相关信息，因此在搜索过程中将会产生不稳定的边界和很多无效的分支，解决这个问题的有效方法是在主问题中加入有效不等式，即缩小主问题的上界。文献[13]采用主问题的线性松弛产生多组有效不等式，但这种方式不能保证cut的有效性，还使得问题的求解规模变大，改进效果并不明显。为了保证问题的规模尽可能小和加入的不等式尽可能有效，设计基于加入有效不等式的B&BC，即LR-B&BC，选取含有子问题信息的整个MIP问题的松弛解生成一组有效不等式并加入到主问题中，由于整个MIP问题的松弛解含有更多子问题的信息，因此，与主问题的线性松弛相比，其生成的不等式更有效。

3 算例实验分析

3.1 算例测试集

基于文献[1]的算例集对所设计的算法进行测试，算例集包含两个部分：网络结构数据和与每个网络对应的维护工作数据，算例集对应的时间范围为T=1 000。根据网络节点数量、弧数量、平均作业数量，网络结构数据可以分为8个不同规模的网络，其中1，2，3，4为小网络，5，6，7，8为大网络。

维护工作数据设置了两个时间窗区间，分别为小规模的[1,35]和大规模的[25,35]，即维护作业时间窗分别在两个区间随意选择，每个网络根据[1,35]对应产生10个小规模算例，根据[25,35]对应产生10个大规模算例，其中8个网络对应的80个小规模算例称为算例集1，8个网络对应的80个大规模算例称为算例集2，共计160个算例。

3.2 算法性能对比

实验设定单个算例最大运行时间为1 800 s，单个算例的运行停止条件为Abs(gap)=0.999，即主问题上下界的差值为0.999，此时算例求得最优解。实验程序以Python 3.6作为编程语言，Gurobi 8.0为模型求解工具，处理器为Intel Core i7-4710MQ，内存为4GB，操作系统为Windows 10 Professional(64-bit)。两个算例集在1 800 s内小于gap的解的比例分别如图2和图3所示，两个算例集在1 800 s内的详细运行结果分别如表1和表2所示。

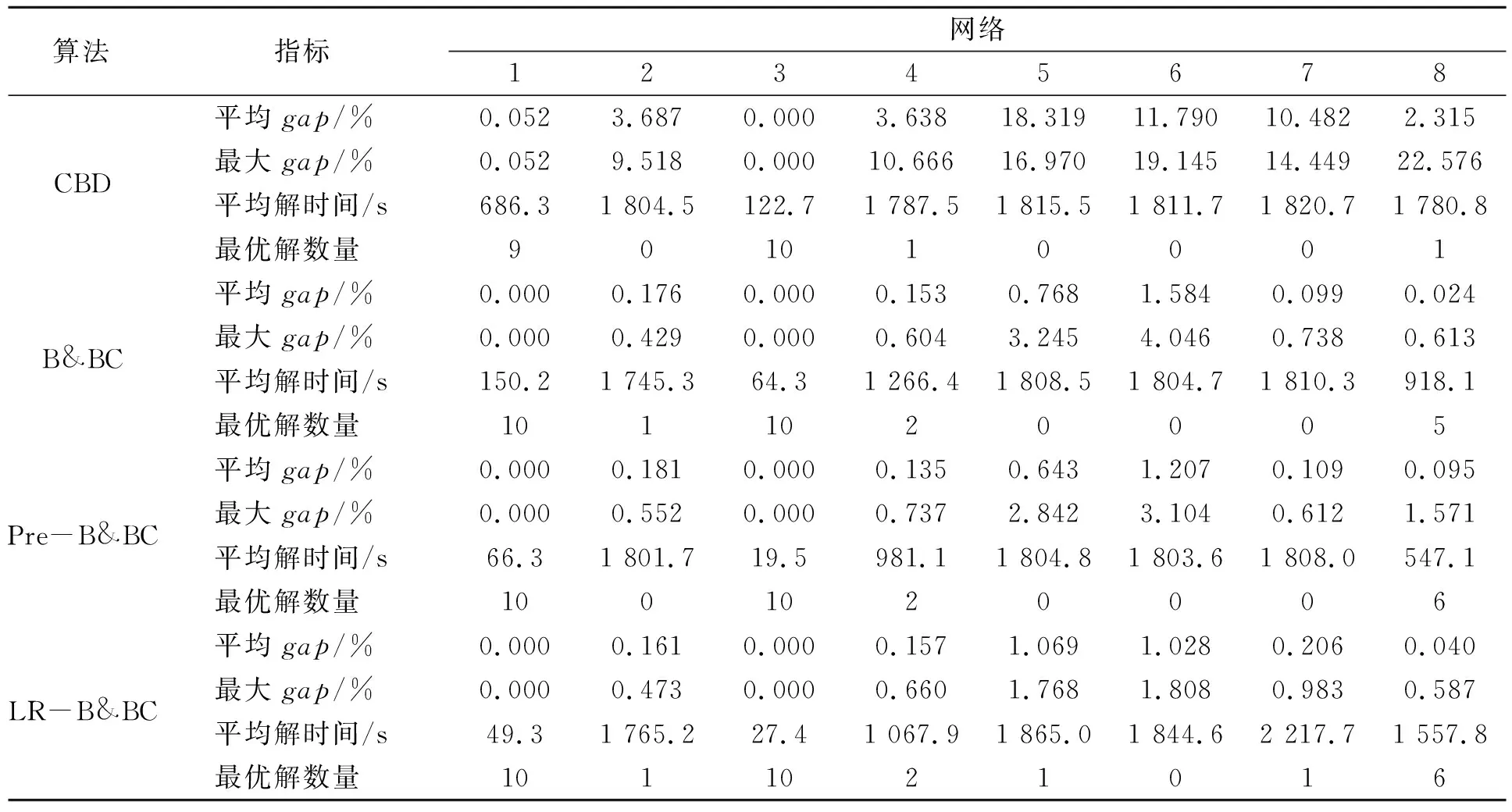
表2 算例集2在1 800 s内的运行结果

图2 算例集1在1 800 s内小于gap的解的比例

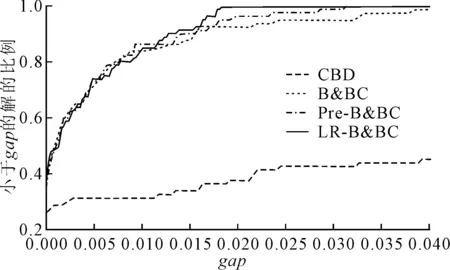
图3 算例集2在1 800 s内小于gap的解的比例

(1)比较CBD算法与B&BC算法。由图2可知，对于算例集1的小规模算例，其求解相对容易，B&BC算法与CBD算法均取得了不错的求解结果，两种算法对于小网络1、2、3均求得最优解，且平均解时间大致相同，最优解求取比例均超过60%。但从表1可以看到，在最难求解的网络5中，B&BC算法的平均gap为0.145%，远小于CBD算法的1.803%。在所有80个算例中，CBD算法的最大gap的最大值为6.263%，B&BC算法的最大gap的最大值仅为0.222%，但在第4个网络上CBD算法求得的最优解个数比B&BC算法多2个。对于算例集2中的大规模算例，B&BC算法所有算例求得最优解的比例为35%，高于CBD算法的26%。B&BC算法的求解优势明显，8个网络的平均gap的最大值为1.584%，小于CBD算法的18.319%。

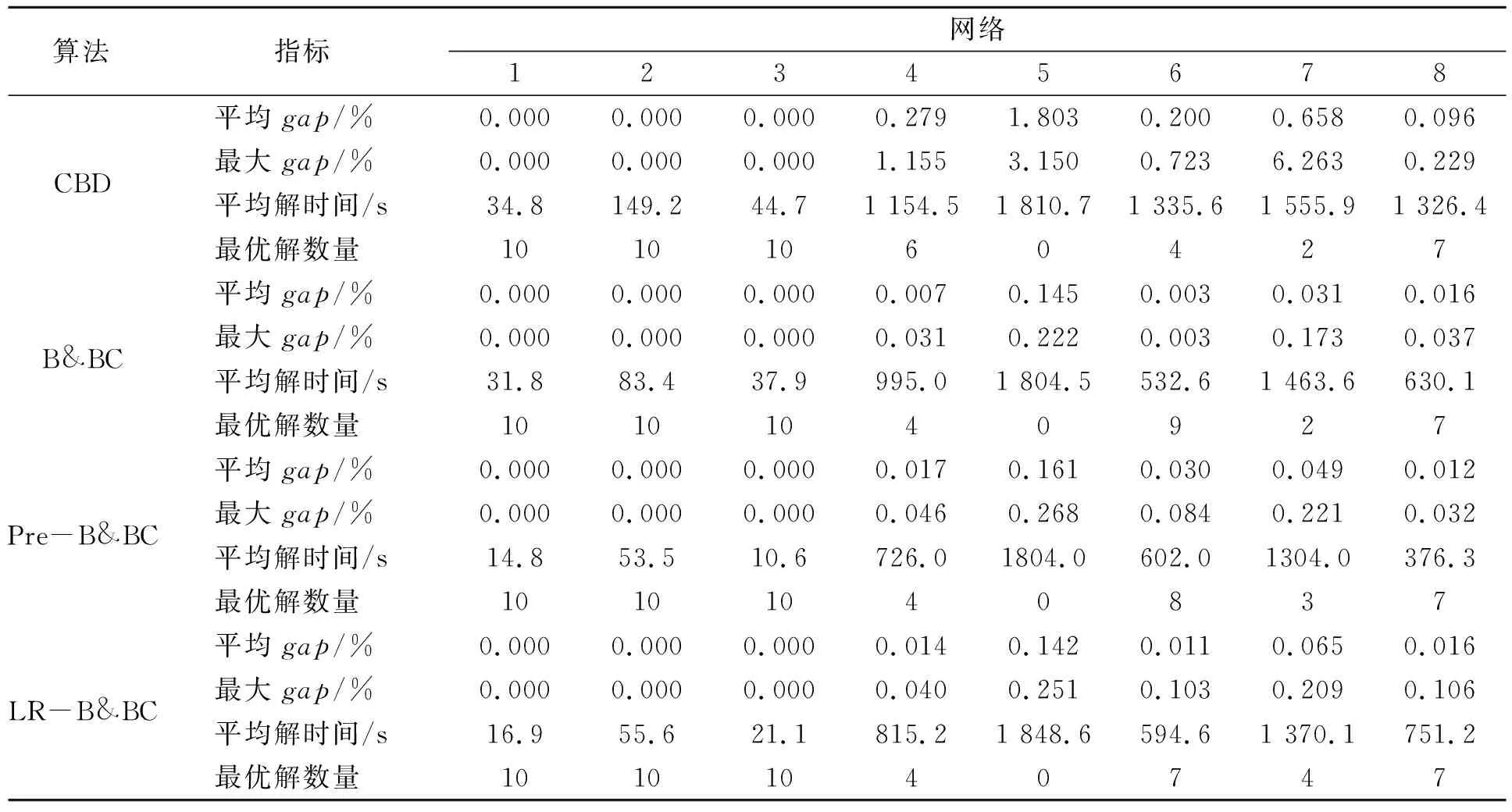
表1 算例集1在1 800 s内的运行结果

(2)比较B&BC算法与Pre-B&BC算法。相比于B&BC算法，Pre-B&BC算法在求解算例集1的小网络1、2、3时，3个网络的总体平均解时间比B&BC算法减少了48%；对于算例集2中的网络1、3，Pre-B&BC算法的平均解时间比B&BC算法分别减少56%和70%。此外，Pre-B&BC算法所有算例的最大gap的最大值为3.104%，较B&BC算法的4.046%下降了23.3%，在算例集2中最难求解的第6个网络，平均gap由B&BC算法的1.584%下降到Pre-B&BC算法的1.207%。

(3)比较B&BC算法与LR-B&BC算法。相比于B&BC算法，LR-B&BC算法在求解小网络时表现出非常大的优势，求解时间明显降低。LR-B&BC算法最大的优势在于求解算例集2的大规模网络, 对算例集2的网络5和网络7分别求出一个最优解，实现最优解求取数量为零的突破。同样对于算例集2中最难求解的网络6，最大gap由B&BC算法的4.046%下降到LR-B&BC算法的1.808%，解的收敛效果提升了59%。

综上所述，整体上B&BC算法比CBD算法在求解结果和求解速度上表现得更好。但是根据算例规模的不同，B&BC算法与CBD算法的求解效果表现出较大的差异，对于小规模算例，此时主问题的规模也相对较小，两者求解差距很小，甚至CBD算法有时会求出更多的最优解。但是当主问题规模较大时，B&BC算法的求解优势则更加明显。此外，相对于B&BC算法，LR-B&BC算法、Pre-B&BC算法在解的收敛速度方面均有一定提升，Pre-B&BC算法在求解小规模网络时，求解时间的提升尤其明显，LR-B&BC算法则在求解大规模问题上表现出显著的求解优势。

4 结论

针对煤炭供应链网络设备维护调度问题，考虑其特殊的网络流与调度相结合的结构，设计了CBD、B&BC两种Benders分解算法。通过算例求解发现B&BC算法在总体上表现出更好的求解效果。基于这一研究结果，在原有B&BC算法基础上，使用预流推进算法对子问题的求解进行改进，重点针对主问题的求解设计了一种改进方案即加入一组有效不等式。最终通过算例实验分析，得到以下结论：

(1)通过具体分析160个算例的求解数据，认为在煤炭供应链的实际工业应用中，CBD算法可能更适合求解子问题相对规模较大的网络，而B&BC算法更适合求解主问题规模较大的网络，即维护调度情况更为复杂的网络，因此建议根据调度问题规模选择合适的算法。

(2)使用预流推进算法对子问题的求解进行改进，发现其更适合加速小规模网络的求解，对大规模网络提升较有限。

(3)通过加速主问题的求解，即加入一组有效不等式，发现此改进适合加速大规模问题的求解，在求解时间充足且希望获得最优解的情形下能取得很好的效果。

但是，由于B&BC算法在Benders分解过程中加入了过多的Benders cut，主问题的规模变得越来越大，导致解的收敛性逐渐变慢。因此在未来的研究中，可以考虑针对加入的Benders cut设计有效的筛选方案，以达到更高的求解效率。此外，B&BC主问题的分支与节点选择策略、解生成策略的智能化研究略有不足，使用机器学习算法对主问题的求解过程进行有效干预也会成为未来研究的重点。