以旧换新的两阶段闭环供应链博弈策略分析

司凤山，王 晶，戴道明，王 娟

(1.安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030；2.北京跟踪与通信技术研究所，北京 100094)

随着经济的快速发展和人们生活水平的不断提高，产品的更新换代正在加速。大量废旧产品的存在已造成环境污染和资源浪费，因此有必要采取措施加大废品的回收和利用。通常，制造商、零售商或第三方回收商以具有吸引力的价格从消费者手中直接回收废品用于再制造。但是由于消费者对再制造产品的质量存在顾虑，有限的市场需求限制了废品的回收利用。为了提升再制造产品的市场占有率，实施以旧换新不失为一种良策。

关于以旧换新的研究，胡强等[1]在考虑产品以旧换新的基础上，研究了3种博弈模式下产品绿色水平、零售价和返利价格的最优决策问题，对比分析了产品零售价和制造商利润在不同情形下的优劣关系。顾巧论等[2]分析了参考因素对实施以旧换新的影响，讨论了二手市场的销售价格、财政补贴和废品再利用等方面的以旧换新措施。韩小花等[3]研究了两阶段闭环供应链中以旧换新策略的实施条件，探究了制造商和零售商的最优定价策略，设计协调机制实现制造商和零售商的共赢。缪朝炜等[4]在闭环供应链中考虑以旧换新策略，对比分析了3种不同模式下的最优定价、回收策略和利润情况。刘靓晨等[5]考虑策略型消费者的理性预期，通过建立两阶段动态博弈模型研究以旧换新时的最优产品换代与定价策略问题。吴鹏[6]研究了基于以旧换新策略的双寡头价格和利润的博弈行为，分析了消费者效用、竞争强度等因素对定价和以旧换新折扣策略的影响。马卫民等[7]从消费者、企业和供应链规模3个方面，分析了政府补贴和消费结构变化对以旧换新闭环供应链的影响。MA等[8]研究了以旧换新的最优定价问题，给出了企业选择合适交易方案的条件。颜波等[9]在考虑消费者净效用的基础上构建了制造商以旧换新策略模型，研究了双渠道中以旧换新的策略问题。李春发等[10]研究了家电企业实施以旧换新策略下的集中决策问题，给出了废品最优回收定价策略。

综上所述，现有文献虽然对以旧换新策略下的集中决策、分散决策、协调机制等方面进行了深入研究，但是极少从系统稳定性的角度对以旧换新博弈模型进行动态策略均衡分析，没有体现出制造商和零售商的价格博弈是一个长期反复的策略动态调整过程。以旧换新策略能够促进废品的回收和再制造，制造商因而得到政府依据废品回收数量给予的补贴，但是新产品和再制造产品的并行销售必然造成两者之间存在价格竞争关系。因此，针对已有研究只考虑决策者完全理性预期假设的不足，对于新产品和再制造产品之间的价格博弈问题，笔者不但给出制造商和零售商完全理性下的最优定价策略，而且刻画出双方有限理性下策略的动态调整过程，从系统稳定性的角度描述价格博弈行为，以期为制造商和零售商价格决策提供参考。

1 模型与假设

研究的供应链模型由一个制造商和一个零售商组成，制造商负责生产新产品和再制造产品，零售商负责两种产品的销售。第一阶段，制造商以单位成本c1生产新产品，将新产品以批发价w1提供给零售商销售，新产品的零售价为p1，市场需求量为d1；第二阶段，制造商以单位价格pr回收废品用于再制造，回收量为qr，单位再制造产品的成本为c2(不含参与再制造的废品成本)，制造商以价格w2将再制造产品批发给零售商销售，再制造产品的零售价为p2，市场需求量为d2。政府依据回收的废品数量对制造商进行补贴，单位废品补贴标准为v。虽然消费者以价格p2购买再制造产品，但是由于制造商会以合理的价格pr回收其废品，所以消费者在购买再制造产品时达到了以旧换新的效果，即以低于市场价的价格p2购得再制造产品。两阶段闭环供应链模型如图1所示。

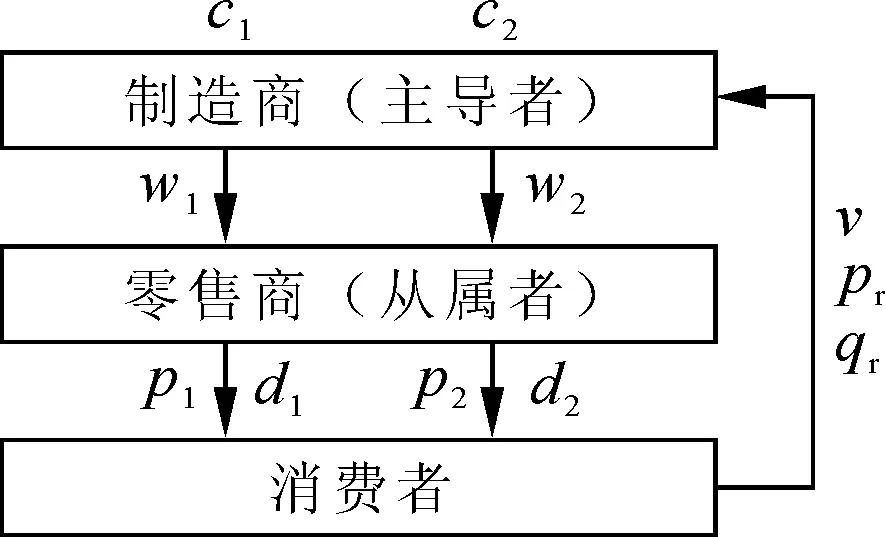
图1 两阶段闭环供应链模型

笔者对两阶段闭环供应链模型做出如下假设和说明：

(1)为了扩大再制造产品的市场需求，只允许消费者在购买再制造产品时制造商才会回收其废品，其他情形制造商不收废品。

(2)由于加工材料和制造工艺的差异，两阶段单位产品的制造成本不同，即c1>c2，从而w1>w2，p1>p2；为了制造商和零售商能够获利，则有p1>w1，p2>w2。

(3)仅考虑大件产品的回收和再制造，例如冰箱、空调等，即单位的废品参与生产单位的再制造产品。

(4)假设制造商和零售商在博弈过程中处于权利不对等的地位，制造商为主导者，零售商为从属者，即双方的博弈过程为Stackelberg博弈。

(5)在两阶段Stackelberg博弈中，第一阶段为主导者，第二阶段为从属者；在两个阶段中，制造商是主导者，零售商是从属者。

2 单阶段博弈模型分析

假设制造商和零售商为完全理性的决策者，双方能够完全掌握决策所需要的市场信息。在第一阶段，制造商先确定新产品的批发价w1，然后零售商再确定零售价p1；在第二阶段，制造商先确定废品的回收价pr和批发价w2，零售商再确定零售价p2。两个阶段都采用线性的需求函数[11]：

di=ai-bpi，i=1,2

(1)

式中：a1为新产品的最大市场需求量，a1>0；a2为再制造产品的最大市场需求量，a2>0；b为价格敏感系数，b>0。

第二阶段消费者以旧换新提供的废品量为：

qr=α-β(p2-pr)

(2)

式中：α为潜在参与换购的废品数量,α>0；β为价格敏感系数，β>0。消费者提供废品的数量qr与零售价p2和回收价pr的差值负相关，理想情况为p2=pr，即消费者不用另外付费即可获得再制造产品，此时所有的潜在废品都参与了换购。

制造商和零售商的利润分别为：

πM=(w1-c1)d1+(w2-c2)d2-prqr+qrv

(3)

πR=(p1-w1)d1+(p2-w2)d2

(4)

式中：πM为制造商利润；πR为零售商利润。为便于计算，假定废品的回收价格pr=θp1，θ为废品回收价格系数，θ∈(0,1)，即制造商按照新产品零售价的θ倍回收废品。

2.1 无协调机制的情形

无协调机制情形下(用字母N表示)，制造商不对零售商进行补贴。

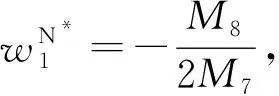
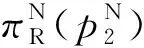
(5)

(6)

将式(6)代入式(5)可得：

(7)

在第一阶段中，将式(6)和式(7)代入式(4)可得到零售商的利润为：

(8)

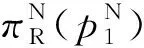
(9)

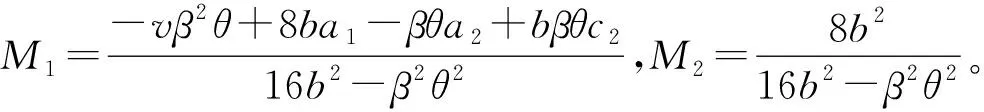
再将式(9)分别代入式(6)和式(7)可得：

(10)

(11)

式中：M3=[4bβθa1+(8b2-β2θ2)a2+4b2(2bc2-2vβ)]/(16b3-bβ2θ2),M4=4b2βθ/(16b3-bβ2θ2)，M5=[2bβθa1+(12b2-β2θ2)a2+2b2(2bc2-2vβ)]/(16b3-bβ2θ2),M6=2b2βθ/(16b3-bβ2θ2)。

将式(9)～式(11)代入式(3)，则可得到制造商的利润为：

(12)

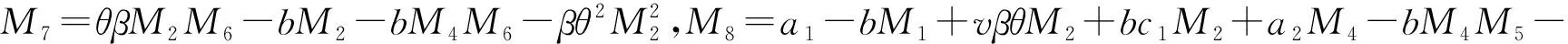
(13)

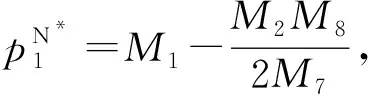
命题1得证。

此时，将两阶段的最优批发价和最优零售价代入式(3)和式(4)，即可得到无协调机制情形下制造商和零售商的最优利润。

2.2 有协调机制的情形

为了激发零售商销售产品的积极性，使得零售商在废品回收过程中发挥更大的作用，设计一种收益分享协调机制对零售商进行补贴，即制造商只保留回收废品所得政府奖励的一部分收益γqrv，而把(1-γ)qrv的收益分享给零售商，其中γ为收益分享协调比例。在协调机制情形下(用字母Y表示)，制造商和零售商的利润分别为：

(14)

(15)

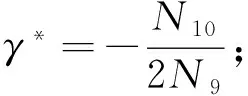
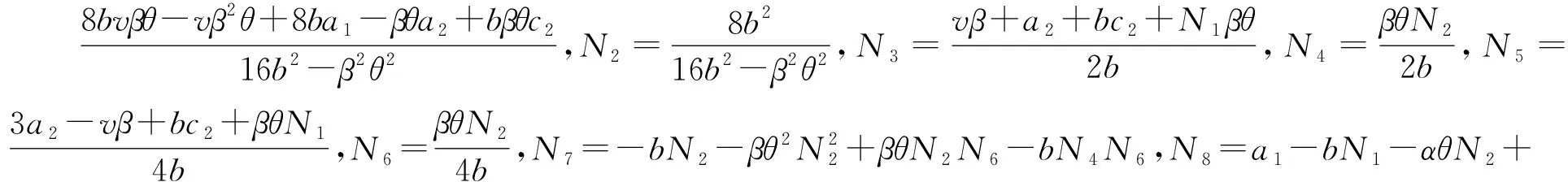
此时，将命题2中的最优策略代入式(14)和式(15)，即可得到协调机制情形下制造商和零售商的最优利润。

3 多阶段博弈模型分析

命题1和命题2中的最优策略是制造商和零售商最理想的博弈结果，实际上需要决策者经过长期的、反复的策略调整才能得到。为了描述策略调整的过程，构建多阶段的动态博弈模型，借助时序图刻画系统从初始态到均衡态的演化过程。

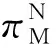
(16)

(17)

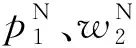
式(17)可线性化为：

(18)

则式(18)的特征方程为：

(19)

4 数值仿真及分析

在满足假设(2)、命题1和命题2条件的基础上给模型中参数的取值，通过数值仿真探讨最优策略和最优利润的演化行为。参数取值如下：a1=2，a2=1，b=1，α=0.6，β=1，θ=0.3，v=0.6，c1=1，c2=0.8，k=0.5；无论有无协调机制，两个阶段价格的博弈初值均为：w1=1，p1=1.493，w2=0.824，p2=0.912。

4.1 单阶段模型仿真分析

(1)废品回收价格系数θ对最优利润的影响。根据上述分析可知，θ越大意味着废品回收价格越高，消费者得到的收益就越大，换购再制造产品的意愿就越积极。有无协调机制下θ对制造商和零售商利润的影响如图2所示。

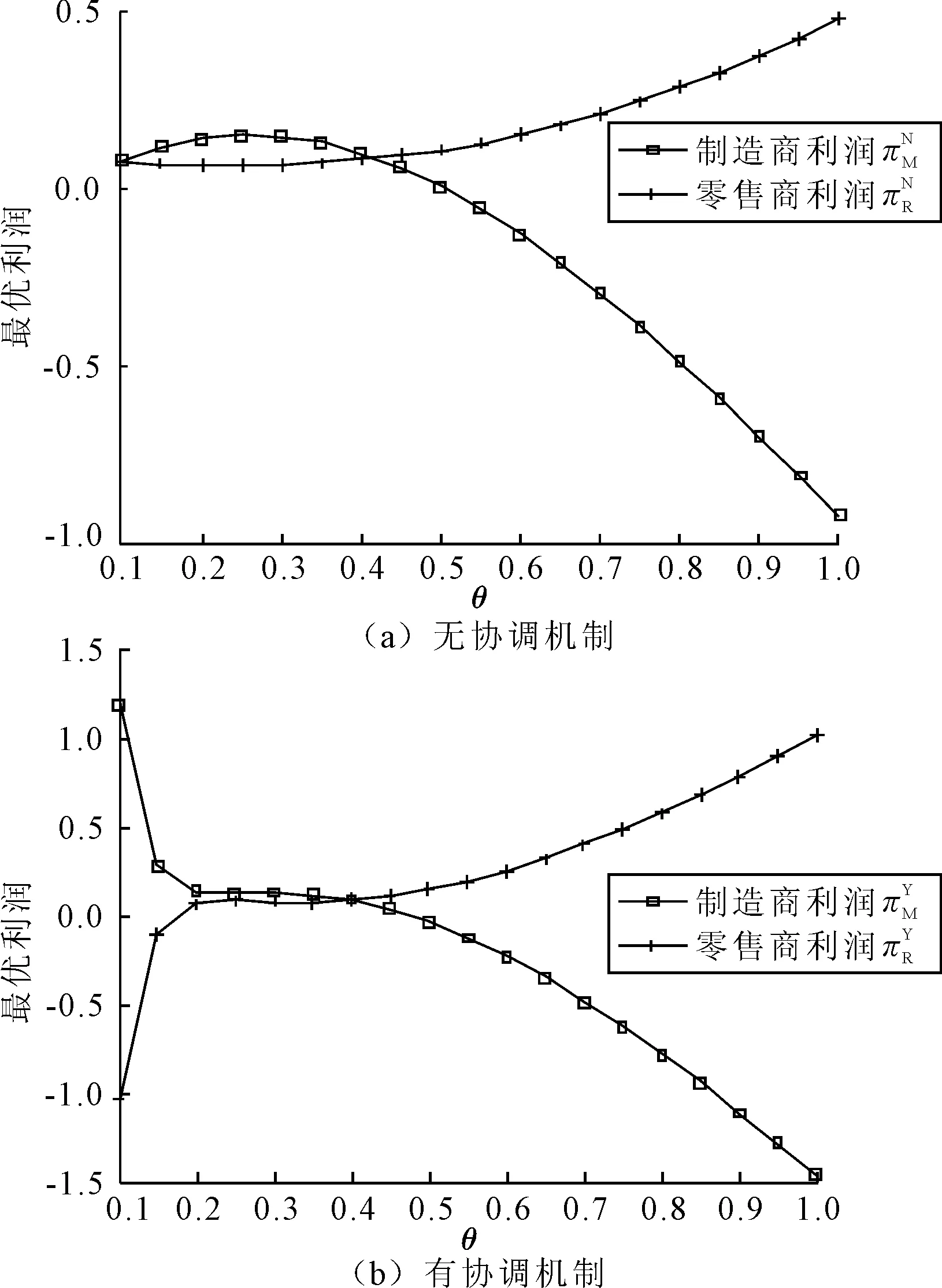
图2 废品回收价格系数对最优利润的影响

从图2可以看出，无协调机制下，存在最优的废品回收价格系数使得制造商的利润最大。有协调机制下，制造商利润明显下降而零售商利润则显著增加。无论是否存在协调机制，废品回收价格系数的增加都会引起零售商利润的增加，但是制造商利润则会随之下降。

(2)单位废品补贴标准v对最优利润的影响。有无协调机制下单位废品补贴标准v对制造商和零售商利润的影响如图3所示。从图3可知，无协调机制下，制造商利润与单位废品补贴标准v正相关，而零售商利润则随着v的增加先降低后增加，即存在一个阈值使得零售商利润最小。有协调机制下，制造商利润则随着v的增加先降低而后上升，即存在一个阈值使得制造商利润最小，而零售商利润则恰恰相反，即存在一个最优值v使得零售商利润最大。这说明，无论是否存在协调机制，单位废品补贴标准v越大对制造商利润增加越有利，但是零售商利润在两种情形下的变化趋势截然相反，总体而言有协调机制更能促进零售商获利。

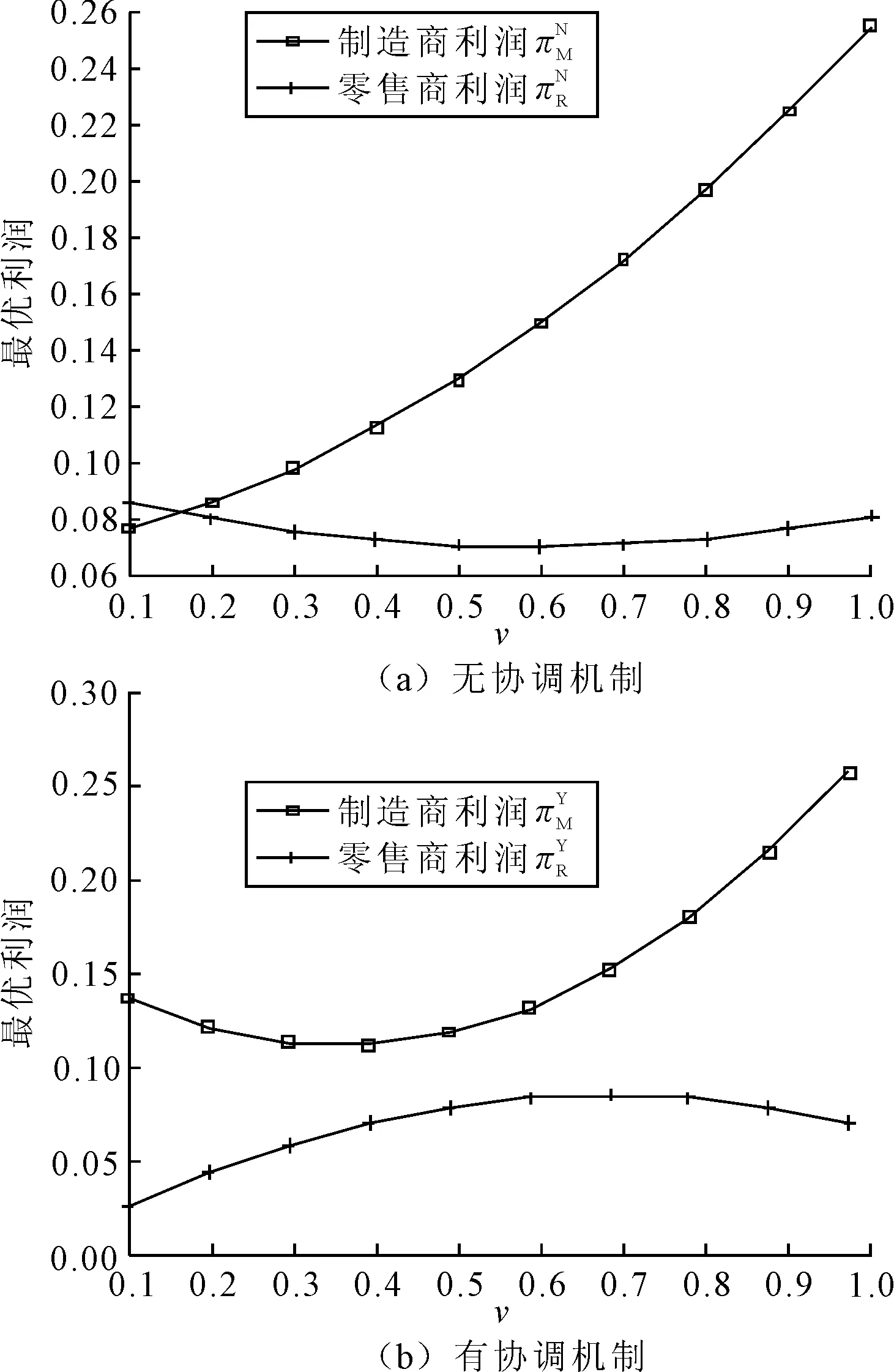
图3 单位废品补贴标准对最优利润的影响

4.2 多阶段模型仿真分析

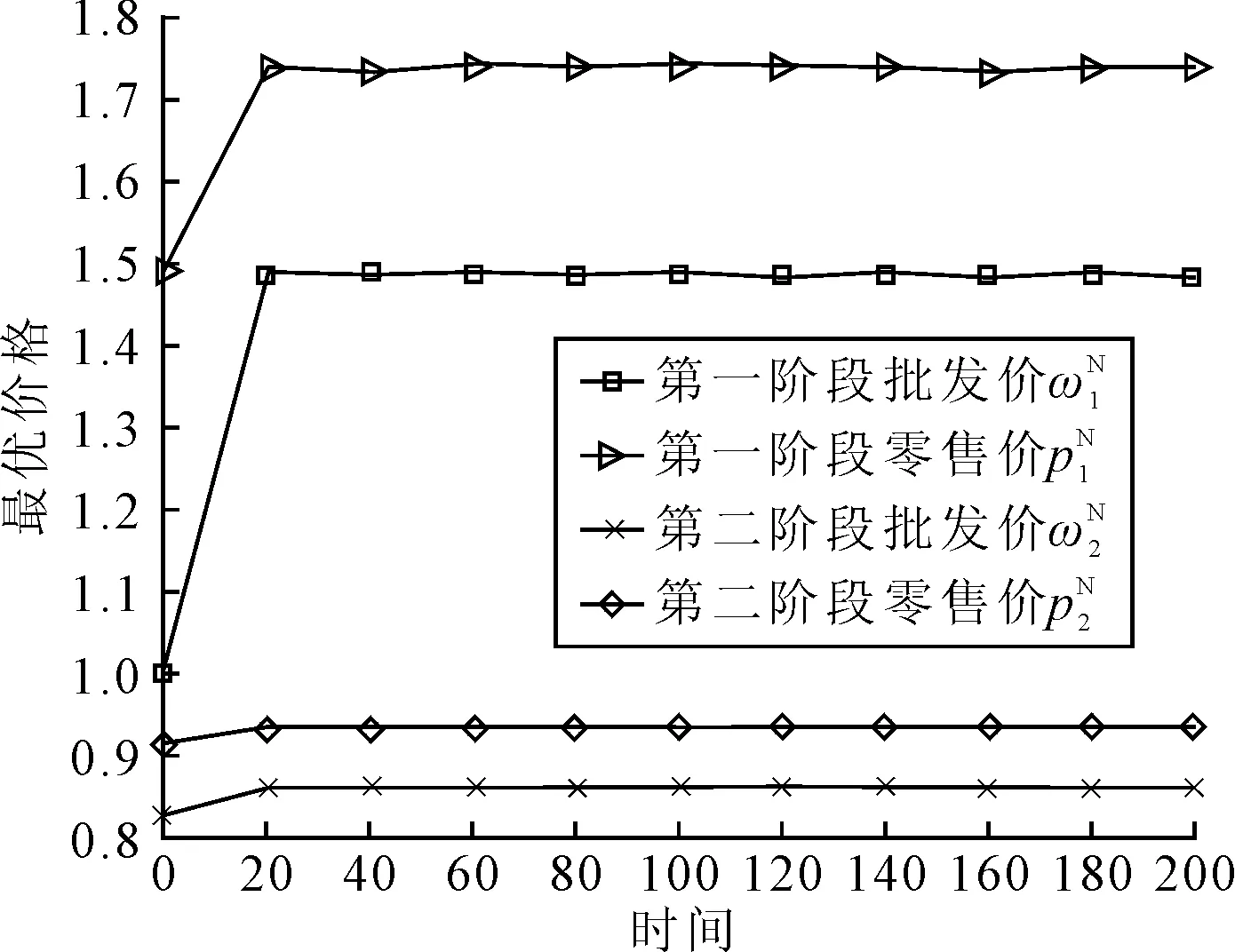
图4 价格变化的时间序列图

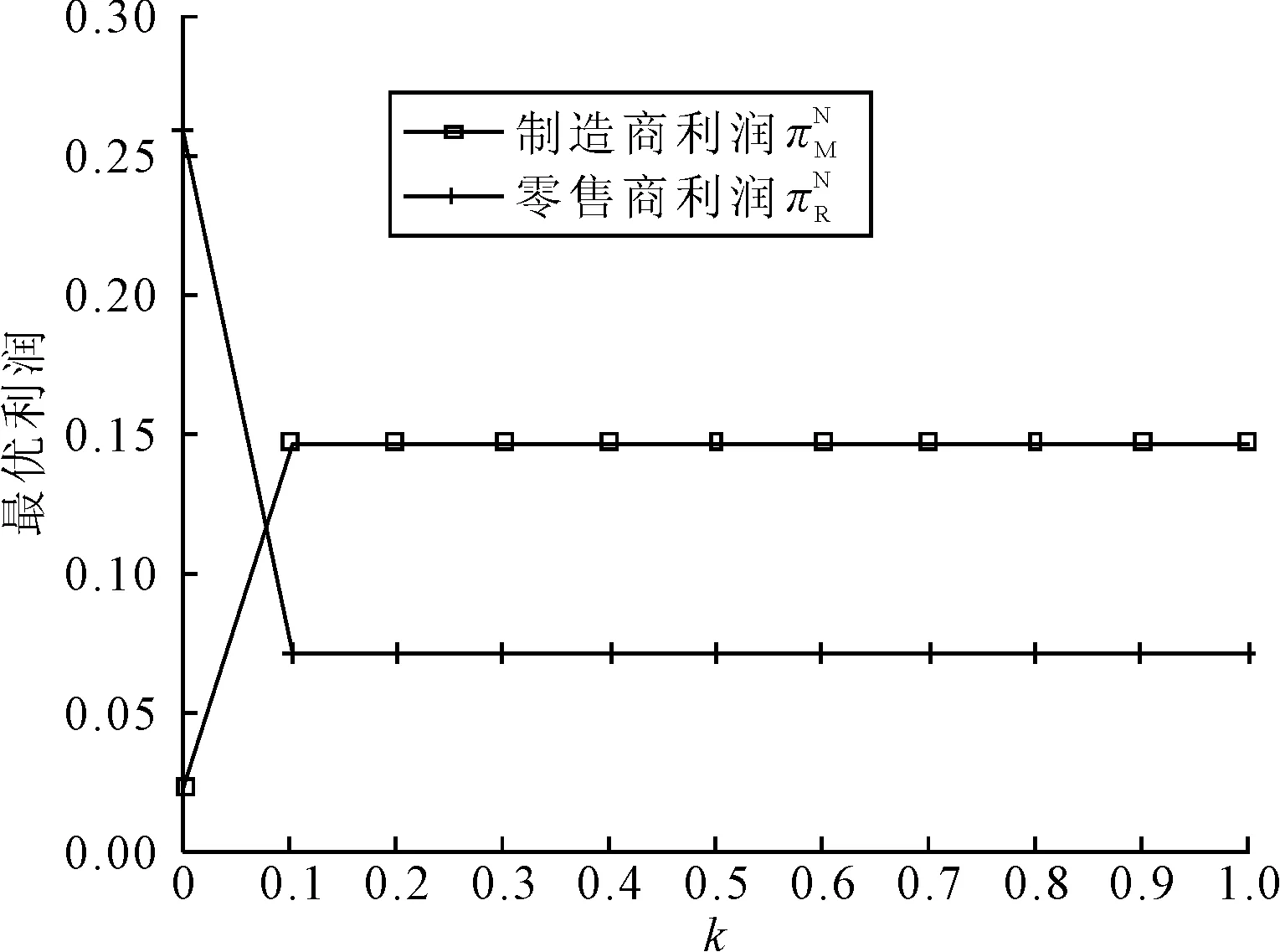
图5 价格调整速度对利润的影响

图4和图5中策略的博弈行为，都是以系统稳定为前提的。从图4可以看出，两个阶段的价格都是从初始态经策略不断调整后趋于均衡态，显然第一阶段的批发价和零售价都大于第二阶段的批发价和零售价，且各阶段的零售价都大于对应的批发价，这符合实际且与假设(2)一致。图5描述了制造商利润和零售商利润随价格调整速度k变化的行为，在博弈初期制造商的利润与价格调整速度正相关，而零售商利润则与其负相关，当k=0.1时双方利润进入均衡状态，这也是制造商和零售商的利润最佳值，此时双方都不愿主动采取措施改变这种均衡状态。

5 结论

(1)在考虑消费者以旧换新的基础上，将制造商和零售商的博弈行为分为两个阶段来研究，构建单阶段Stackelberg博弈模型，给出制造商和零售商的最优博弈策略解析式，并设计协调机制实现制造商和零售商的收益分享。研究结果表明，提高废品的回收价格有利于增加零售商利润，协调机制下增加更明显；提高单位废品补贴标准会同步增加制造商利润和零售商利润，但协调机制下制造商利润增长放缓，而零售商利润则增加明显，并存在最优补贴标准使得零售商利润最大。

(2)建立无协调情形下的多阶段动态Stackelberg博弈模型，描述了价格和利润从初始态到均衡态的博弈演化过程。研究结果表明，制造商和零售商在单阶段博弈中得到的最优价格和最优利润，在实际市场中是需要双方经过长期不断的策略调整才能达到；制造商和零售商从初始态到均衡态的博弈行为是以系统稳定为前提的。

(3)笔者只研究了再制造产品的以旧换新策略，针对新产品的以旧换新将是未来的研究方向。