基于改进K-means聚类算法聚类点选取办法的研究

◆任楚岚 乔天宇 张 阳

( 1.沈阳化工大学计算机科学与技术学院 辽宁 110142; 2.辽宁中医药大学附属医院 辽宁 110032 )

1 背景介绍

现有的聚类算法中，K均值聚类已成为使用最广泛的技术之一，主要是因为其简单性和有效性。在K均值聚类中，有两个典型的阶段，即聚类初始化和迭代优化。在集群初始化中，首先应随机或根据某些标准确定一组K个集群中心。聚类结果K个聚类中心将通过将每个数据对象迭代地分配给它最近的聚类中心并更新聚类中心的集合而得到优化。K均值的迭代优化算法对数据初始聚类中心非常敏感。一组初始化不佳的聚类中心会降低K均值性能。

为了解决K均值存在的初始化问题，利用不同的技术进行尝试。由于在聚类中心选择中通常会存在一些随机（或概率）决策，因此这些方法还会遭受随机性带来的不稳定性。这里的问题是我们是否可以将可能不稳定的多个初始化合并到一个更好、更健壮的初始化中，以增强 k-means聚类的整体性能。Arthur和Vassilvitskii 提出了 k-means ++的办法，该方法随机选择第一个聚类中心，然后根据一定的概率选择第i个聚类中心。数据集中的对象与先前选择的i-1中心之间的距离。

基于此种方法集合聚类技术的启发也称为无监督集成学习，旨在将多个弱聚类组合成一个更好的聚类，在本文中，我们通过将多个K均值实例集成到一个集成框架中，提出了一种改进的K均值初始化方法。具体来说，我们首先从数据集中随机选取一个样本作为初始聚类中心C1。对于数据集中的每一个点Xi，计算出它和当前已有聚类中心之间的最小距离。用D（X）表示。然后选择一个新的样本为新的聚类中心，一般选取距离D（X）大的点，被选取作为聚类中心的概率较大。通过重复以上的步骤，选出K个聚类中心。我们在多组真实事迹的医疗数据集上进行了实验，证明了所改进的K均值初始化方法能够比其他几种初始化方法产生更好的性能。

2 构建方法

2.1 由多个K-means聚类器生成的集合

K均值聚类对初始聚类中心的选择高度敏感。即使使用相同的初始化策略，在多次运行中获得的初始群集中心的集合也可能会非常不同，许多初始化方法中固有随机性会导致最终K均值聚类结果不稳定。

本文采用多种初始化来获得鲁棒集群中心初始化结果。我们多次执行K均值聚类（使用随机初始化）以获得各种基础聚类的集合。每个K均值聚类器的聚类数也可以随机选择，以进一步改善生成的基本聚类的多样性。

令D= {D1，D2，...，DN}表示数据集，其中DN是第N个对象，是数据集中对象数量。km表示均值聚类器聚类数，它是在[kmin，kmax]范围内随机选择的。

δ∈[0，1]是随机变量，从随机选择的初始聚类中心开始，执行K均值聚类以获得第一个基本聚类，表示为：

表示第一个群集，并表示第一个基本群集中i-th的群集数量。通过执行 K均值聚类时间，可以由此获得基本聚类的整体，表示为：

2.2 通过排除干扰点进行预聚类

基本聚类集合构成之后 K-means算法对孤立点是十分敏感的。因此在获得基本的聚类集合之后，获得了基本聚类的集合后，接下来借助排除干扰的孤立点构建和聚集聚类来构建预聚类结果。

本文基于密度思想，需人为给定半径r和最小邻域点数MinPts。以空间的某一点为球心，r为半径的球体，给定半径r的邻域。用Nr(p)来表示该邻域里的点p在半径r的范围里所有点的集合。表示为：

用D(p,q)表示两点之间距离，V为数据集的容积，n为样本个数，d是样本维度，Γ为伽马函数。MinPts为该邻域内核心点的最小邻域点，MinPts的值根据数据集中的数据多少而定。

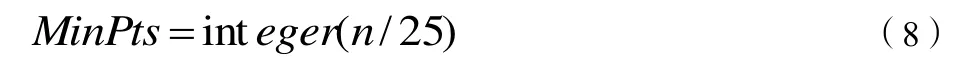
通过这一办法，将数据样本集分为核心点、边界点和孤立点三类。核心点对我们有帮助，为了达到有效的聚类效果，要排除集合中的孤立点和边界点，取集合簇中核心点的中心作为新的聚类中心。

根据预聚类结果，计算中的每个聚类的欧几里得中心，获得K个聚类中心集，表示为：

K个聚类中心结合了多种方法得到的，具有随机初始化的多个K均值聚类器中，然后将这K-means聚类群集中心用作初始群集中心在最终的K均值过程中获得强大的聚类结果。我们将评估针对预聚类结果的方法以及其他几种初始化方法的K均值。

3 实验分析

本节检验了改进算法的有效性，对原始算法和改进算法进行对比实验。

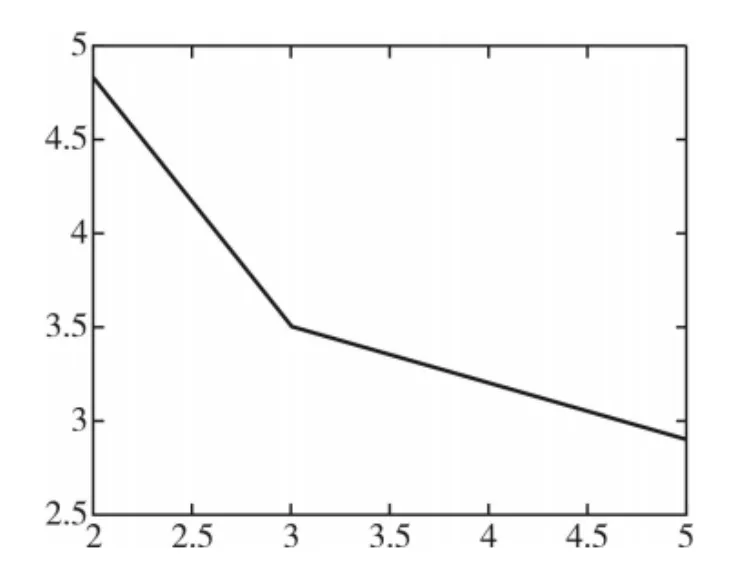
图1 类簇指标的变化曲线

由图1可知，在不同的聚类数目类簇指标下，可以清楚地看到在K=3的时候，出现拐点。类簇指标有明显改变，故K=3。

为了验证结果的可靠性。分别代入两组不同数据（数据 A ，数据B）进行传统K-means聚类算法和改进后的K-means聚类算法两组实验，并对两组实验的准确率进行对比。

表1 数据A的对比实验

表2 数据B的对比实验

通过两组实验，我们可以看出：传统的K-means算法，相同数据集条件下，不排除孤立点和边缘点，效果不佳，对实验整体影响很大，准确率不如改进的算法。

4 结语

本文采用基于密度的方法，改进集群中心初始化集成学习的K均值聚类方法，先是利用随机初始化的办法，再利用多个K均值聚类器和随机数的簇，M个基的整体生成聚类。在此聚类的基础上，结合基于密度的方法，排除孤立点和边缘点。最后，再通过对比实验验证了改进后的算法，结果强于传统的K-means聚类算法。