掘思维“源头”,引思维“活水”
2020-07-17陈云
陈云
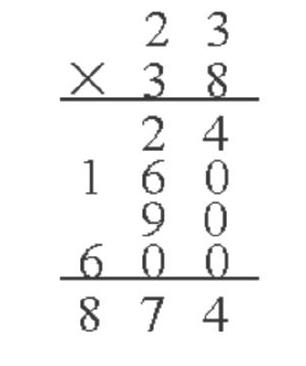
摘要:学校教育的首要任务是培养和提高学生的能力,而数学教学中学生能力的提高关键就在于数学思维的培养。问题“建模”是数学思维的基本形式,这个从具体的、熟知的生活情境中提炼、抽象、概括出“模式”的过程,能让学生的比较、分析、抽象、概括等数学思维得到有效训练。活动“内化”是数学思维的重要内涵,也就是要在教学中通过“同化”“顺应”使新知和已有认知结构发生联系,从而达到对新知的“内化”。策略“化归”是数学思维的本质要求,长期坚持,学生的观察、猜想及逻辑论证等能力都会有所提高。
关键词:数学思维;问题建模;活动内化;策略化归
数学思维能力僵化现象在现代学生中是大量存在的,这与学生平时所受的思维训练有很大关系。教师在教学过程中过分强调程式化,不断给学生归纳各种题型,学生只会按部就班地解题,知其然不知其所以然,这样的教学使学生的思维缺乏应变能力,在面临问题时就不能够从多种角度进行思考,并迅速建立起自己的思路,真正做到举一反三。如何更好地培养学生的数学思维能力?本文从数学思维的形式、内涵、本质要求三个方面对此进行阐述。
课程改革十余年,在探索前行中,仍有一些现象需要审视。在教学对象上,同一起点的学生由不同的教师教,思维存在较大的差异;在教学效果上,重负低效、轻负高效反差明显;在教学追踪上,高分低能、越学越差的现象仍有发生……如何有效净化滋生这种现象的土壤,掘思维“源头”,引思维“活水”呢?这就要求耕耘在一线的老师不仅要了解数学教学内容本身的规律和含义,还要切实树立整体和长远的观念,不断地挖掘数学思维的素材,寻找培养数学思维的切入点。只有这样才能达到《数学课程标准》中所要求的:“让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程,进而使学生获得对数学理解的同时,在思维能力、情感态度与价值观等方面得到进步和发展。”
一、问题“建模”是数学思维的基本形式
数学是“模式”的科学,数学教学不能仅仅让学生单纯地去探究某个现实情境中特定的、单一的问题,而要从“某个”“某种”过渡到“某些”“某类”,从而抽象为普遍的“模式”。其间从具体的、熟知的生活情境中提炼、抽象、概括出“模式”的过程就是问题“建模”,这是数学思维的基本形式。如在“分类”知识的教学中,针对低年级学生,教师会引入丰富的现实情境,从整理房间、整理书包入手:用学具代替物品分一分、摆一摆;把书包里的东西倒出来整理一下……这种鼓励学生用“实践”的方法去解决问题的方式是可取的,但如果就此收兵,学生获得的就仅仅是单一的、浅表的分类结果。倘若此时改变情境,让学生给花园里的花、森林里的动物、操场上的人分类……学生拿出学具,却一脸茫然:“老师,我的学具不够怎么办?”“老师,我忘了带动物卡片,这可怎么摆啊?”“老师,操场上又是老师,又是小朋友,这可怎么分呢?”……缘何学生的思维停留在初级的实践阶段,还是需要依靠老师的提示去摆一摆、圈一圈、连一连才能得出结果呢?如果在整理房间、整理书包后,教师及时引导反思:“你是如何整理的?”“整理时只有一种分类方法吗?”“你用什么方式把分类的结果直观、简洁地表示出来?”……学生通过比较两次整理活动,从中发现、总结出分类的思维程序:“我知道:整理时首先要确定分类标准。”“原来同一些物品可以有不同的分类标准呀!”“确定了标准,还要划分出合适的类别呢。”“我喜欢用序号法表示分类结果,就是先给要分类的东西编上序号……”“我认为集合图更直观……”这些表述说明学生的思维超越了具体问题,上升到抽象的高度,从而在这些“分类”的不同问题中揭示出它们事实上具有相同或类似的数学结果。这时候,再出示后面的几个问题,学生就不需要摆学具、圈图画,而能理性地进行分类了。在这个问题“建模”的过程中,学生不但获得了分类的结果,更重要的是比较、分析、抽象、概括的数学思维得到了有效的训练。
二、活动“内化”是数学思维的重要内涵
著名哲学家、儿童心理学家皮亚杰早就明确指出了“内化”对于数学学习活动的特殊重要性。皮亚杰认为,新的知识只有纳入到原有知识结构中才能被吸收,同化和顺应是使新知识和已有认知结构发生联系的过程,也就是内化的过程。例如,在“面积的计算”教学中,教师给出几个不同大小的长方形,如何得到它们的面积?经过上节课的学习,学生会想到去进行实际的操作(用1平方厘米的小正方形去铺需要测量面积的几何图形),第一个图形铺一次,第二个图形“依葫芦画瓢”再铺一次,第三个图形不厌其烦地又铺一次……虽然这是一种方法,但思维层面始终停留于实际的操作,未能在头脑中实现必要的重构或认知结构的重组。教师在教学中可否考虑:第一个图形用小正方形“满铺”,这是学生的原有认知结构;第二个图形换成稍大些的。“老师,我的小正方形不够用了怎么办?”“我的也是……”学生的认知因新出现的状况而产生冲突,如何變通?“想一想,有没有什么办法,用你手中仅有的小正方形,甚至不用这些正方形,也能测量出这个长方形含有多少个1平方厘米?合作试一试,看哪个小组用的小正方形最少。”学生经历了反复讨论及验证后展示了不同的方法:“我是沿着长铺一行,沿宽铺一列,我们发现如果铺满是5行6列,也就是30个1平方厘米。”“我只用了一个正方形,就是拿这个正方形的边分别去量长方形的长、宽,也能知道铺满是5行6列,所以得出的结果是一样的。”“我们小组根本就没用小正方形,我们直接用直尺量出了长是6厘米,说明能铺6个边长是1厘米的小正方形,再量宽……”此时学生已经由“全铺”过渡到了“巧铺”“意铺”,从多个“巧铺”到单个“意铺”,还在此基础上通过直尺测量实现了由“面”向“边”的过渡。像这样,学生把外界所提供的信息整合到自己原有认知结构内的过程就是“同化”。接下来,不再铺了,老师随意报出一组长、宽,请学生闭上眼睛想象出这个图形,并说说它的面积是多少,为什么。这时信息环境再次发生变化,学生的原有认知结构无法同化新环境提供的信息,这就进入了认知结构进行重组与改造的“顺应”过程。当学生通过想象就能口答出长方形的面积时,面积计算的算理、算法完全得到了“内化”。这个从“全铺”到“巧铺”“意铺”再到“想象”的过程,学生从实际操作逐步过渡到用思维去把握对象,不断地“同化”“顺应”,从而达到新知的“内化”,正是数学思维的内涵呈现。
三、策略“化归”是数学思维的本质要求
解决问题的策略“化归”,往往不是直击问题,而是换道、变形、转化,化难为易、化繁为简、化生为熟……例如,像23×38这样两位数乘两位数的竖式计算教学,“能口算吗?选择合适的方式把你口算的过程记录下来。”学生利用老师提供的点子图、表格等将23×38转化为如下的几道算式:20×30、20×8、3×30、3×8。“我把23×38变成了整十数乘整十数、一位数乘整十数、一位数乘一位数的计算,这样我就会做了。”“那能不能把你的这个计算过程用竖式表示出来?”学生列出了这样的竖式:
“回忆一下23×8、23×30的竖式计算,再把这两个竖式和23×38的竖式计算进行比较,想一想你还可以怎样让竖式简便?”“原来把23×8、23×30这两个竖式合在一起就行了。”“有了数位知识,用十位上的数去乘另一个乘数,积写在十位的下面就行了,个位的0都可以省略呢!”……这些方法都是“化归”法的巧妙运用,以此类推,后面的多位数乘多位数的笔算都可以化归成原先已经得到了解决并较为简单的“一位数乘一位数”的问题。通过这样的教学,长期坚持,潜移默化,学生的观察、猜想、分析、归纳、概括及逻辑论证等数学思维都会“柳暗花明又一村”。
(责任编辑:奚春皓)
