改进遗传算法下的无水港集货路径优化研究
2020-07-17陈淮莉
彭 露,陈淮莉
上海海事大学 物流科学与工程研究院,上海 201306
1 引言
随着21世纪海上丝绸之路的逐步推进,我国沿岸的港口也变得十分繁忙,以至于经常出现拥堵情况,十分影响作业效率,在上海自由贸易区外,繁忙的外集卡也时常出现堵塞。为了解决该问题,近几年来,无水港也在蓬勃地发展。在中国,无水港是指在内陆,依照有关国际运输法规、条约和惯例设立的对外开放的通商口岸。具备有报关、报检、签发提单等港口服务功能,无水港其实就是港口功能向内陆地区的延伸。大部分的无水港都与海港有合作,为客户办理出口退税和报关手续。
而随着中国电子商务企业的蒸蒸日上,中国的很多电子商务产物要走出国门,而大批量电商货物的运输方式都是先通过汽车或者火车集中到较近的无水港,再通过火车运送到沿岸的海港,从而发往世界各地。因为电商产品的特性,很多时候车辆从发货地运往无水港的时候都不能满载,从而降低了车辆的利用率。
国外关于无水港的建设也开启得较早,现在欧洲约有220个无水港,建于1988年,美国也约有380个主要无水港,亚洲地区也有近100个无水港,其中巴基斯坦和印度发展较早,始于1973年,印度最早始于1981年。这些无水港规模大小不一,如欧洲无水港集装箱装卸量从4万吨到190万吨不等,面积从30公顷到200公顷不等。这些国家正在利用无水港发展的机遇,促进国家经济增长。同时,国外的学者也对这一方向进行了探索,Cullinane等[1]提出了无水港实地建设的相关策略和措施;Leachman等[2]对无水港港口集装箱的运输提出了一个非线性数学优化模型;Fan等[3]提出多式联运网络流模型用以解决无水港港口拥堵的问题;Li等[4]对沿江无水港选址建设提出相关研究;Feng等[5]从无水港与海港的相关性进行研究,提出了无水港的空间配置模型。
我国的无水港也在迅速发展,候马陆港与青岛港签署了合作协议,北京朝阳口岸与天津港签署合作协议,金华无水港与宁波港签署合作协议,鹰潭也和厦门签署了合作协议。其他相关的大型水港,如大连港、营口港等也都纷纷和内地的无水港签署相关协议,进行合作,我国学者也在这方面进行了广泛的探索,吴淑[6]对我国无水港投资运行模式进行了相关研究;任伟[7]以天津港为例,提出了内地无水港建设的规划方案;邵静静[8]以西部内陆无水港建设为依托,提出了重庆无水港选址以及集疏运系统优化方案;贾娜娜等[9]在“一带一路”背景下考虑无水港的跨境运输,建立了以降低物流配送成本,最大化时间价值的非线性整数规划模型;方琴[10]以贵州区域为例,阐明了无水港选址的相关注意事项;吉尔德[11]通过对无水港和扩展通道概念的研究,提出了区域的扩展通道模型,从而对无水港的选址作出评估;赵金楼等[12]对无水港集装箱码头分阶段进行路径优化研究;胡文缤等[13]构建无水港与海港集装箱配送路径优化网络,最优化集装箱运输成本。
以上文献对于无水港的研究绝大部分处于理论探索和选址规划层面,还没有从物流运输整体层面,考虑路径和成本优化,构建水路和陆路联运的出口物流配送网络。本文的创新点在于将无水港和电商出口货物集疏运结合起来,运用扫描法和改进遗传算法相结合对集货路径进行二阶段优化,以达到运输距离及运输成本最小化的目的。
并且考虑到电商产品数量少以及海运需拼箱的特性,本文优先对无水港辐射地的货物进行分块收集优化,将货物从起始地串联运输直至无水港,以进一步提高无水港的集货能力,提升作业效率。本文对包括电商货物在内的内陆和无水港之间的货物集疏运都有实际参考价值。
2 问题描述与模型构建
2.1 问题描述
传统的出口电商商品从始发地到无水港采用点对点运输,车辆数量多,但满载率低,从而导致成本高。现在,改进之后的策略是货主联合起来进行拼车,空车从无水港出发,依次经过各个载货点,载上货物之后,返回无水港卸下。因为每辆车都有相应的容量限制,所以需要多辆车一起配送,共同完成配送任务。电商产品的无水港的集货问题一直以来也困扰着无水港管理人员和货主。因为大部分货主都是将货物直接从起始地运送至无水港,从而导致货物满载率不高,对于无水港而言,大批出口货物的不定时到达也给无水港的管理带来了问题。
传统作业方式如图1所示,车辆直接从发货点出发,采用点对点运输。改进后的作业方式如图2,车辆从无水港出发,依次经过沿线的发货点,装货完成之后,返回无水港卸货。
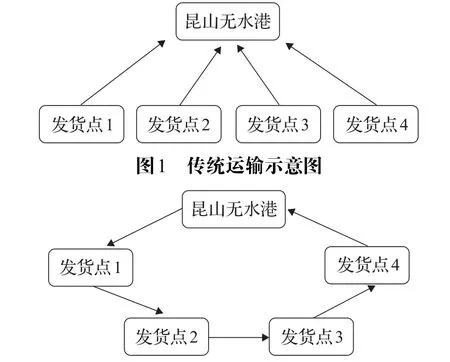
图2 改进后运输示意图
2.2 模型建立
2.2.1 符号说明
参数:
P表示无水港;
i表示发货点;
N表示所有发货点的集合,N=(1,2,…,n);
t表示工作时段,t∈T;
dij表示任意两发货点形成的路径,i,j∈N;
Q表示每辆货车的最大承载量;
qn表示每个发货点拥有的货物质量,n∈N;
Vk表示第k辆车服务的发货点集合;
K表示所有集货运输车辆的集合。
决策变量:
xijk:0-1,若集货运输车辆k经过发货点(i,j),并且顺序从i→j,则为1,否则为0;
yik:0-1,若集货运输车辆k经过发货点i,则为1,否则为0;
zitk:0-1,若在计划时间t集货运输车辆k经过发货点 i,则为1,否则为0。
2.2.2 运输模型
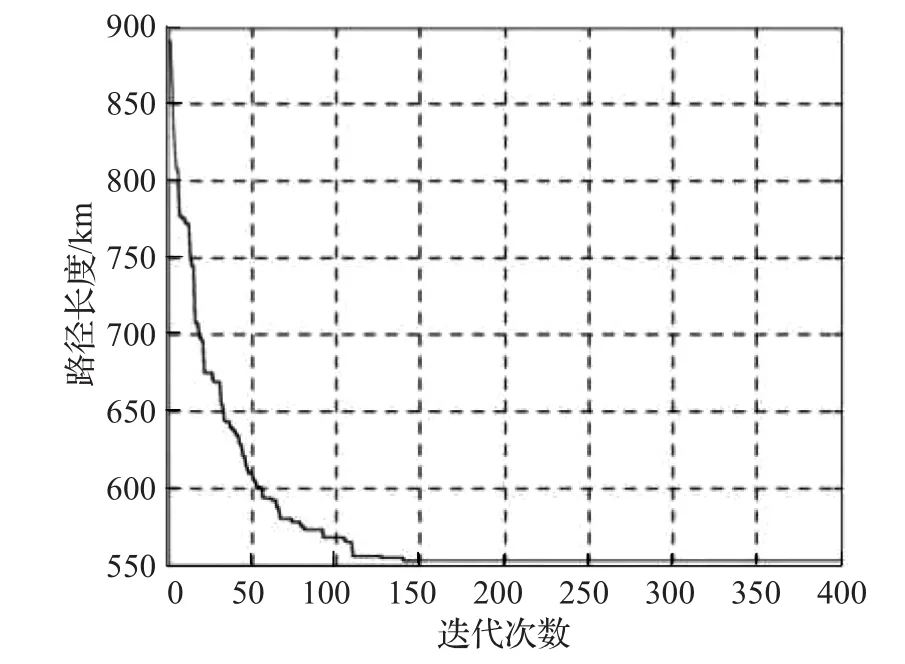
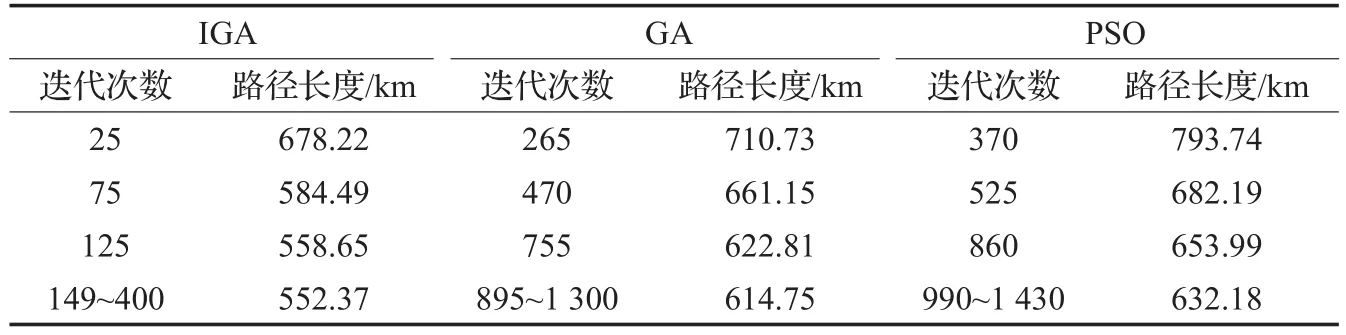
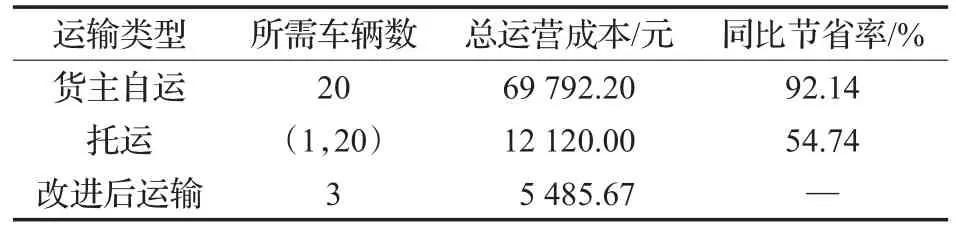
假设max(qi) (1)每辆车都以无水港作为起点和终点;(2)每一个配送点只用一辆车进行服务;(3)每辆车都不允许超过最大载重量。建立运输模型如式(1)至式(7)所示。式(1)为目标函数,表示所有运输车辆的总路程最小化: 式(2)为每辆货车的最大载重约束: 式(3)表示在每一个发货地同一时间恰好由一辆货车提供服务: 式(4)表示在同一时间一辆货车只在一个发货点进行集货运输: 式(5)表示任何一辆集货运输车最多进行一个紧前作业: 式(6)表示任何一辆集货运输车最多进行一个紧后作业: 式(7)表示任一集货运输车通过发货点i,j的先后顺序: 式(8)定义了相关变量之间的关系: 式(9)表示所有车辆起点和终点都在无水港: 式(10)表示每辆车的路径的轨迹都恰好为一个Hamilton简单圈: CVRP问题是一个NP-Hard问题,在经过第一步扫描法分组之后,就将该问题转化为了VRP问题。在这个问题中,伴随着发货点的增加,研究问题的复杂程度将呈指数增长。考虑到传统遗传算法在解决这类问题时运算效率较低、响应慢等问题。在此提出了一种基于最近邻、禁忌搜索和遗传算法的改进遗传算法(IGA),在对初始种群创建方式优化后来加快算法的速度;并且通过改变交叉、变异策略等来改善算法的早熟收敛以及局部搜索较差等问题。 对于每个配送路径中的n个目标,以及无水港,将染色体分为n+1段,其中每一段对应一个发货点的编号。如图3所示,采用整数排列编码,分别表示各辆集货车通过发货点的先后顺序,时段顺序值越小表示越先通过。其中0表示无水港,1,2,…,n表示n个发货点。图3中染色体表示各集货车从无水港出发,第1辆集货车先通过第1个发货点,然后依次经过第7个发货点以及第6个发货点,第2辆车依次经过第3、第2个发货点,以此类推,最终均返回无水港。 图3 染色体编码 随机选取一个发货点作为初始点,通过使用最近邻算法创建初始种群,找到距离它最近的发货点作为次结点,并以此次结点作为初始结点,循环往复找到最后一个发货点,由此创建初始种群。但这样产生的解可能会违反同一时刻同一集货车通过发货点的先后顺序等约束。在此对初始解进行修复。 假设集货车通过发货点2和3,但2先于3,发货点5和7的货物由同一集货车运输。如图4所示,对违反约束的染色体进行修复。 图4 染色体修复 在适应度函数中考虑不可行解的惩罚策略。以所有发货点的货物质量总和不超过车辆的承受范围,以及每条路线的长度不超过车辆的最大行驶距离为双重约束。如果所有发货点均在路线中,则说明该解决方案可行,不可行路线a=0,否则a=1。以Z为目标函数,不可行路径的惩罚权重为M(无限大的正数),解决方案E可以用式(11)表示: 式(12)表示适应度函数。在对染色体个体解码后得到不可行路线的数量a和目标函数值Z。将二者代入方程可得染色体个体的适应度 f。 3.4.1 选择 选择操作也就是从旧的群体中以一定的概率选择个体到新的个体中去,在本文中使用Select函数完成,个体被选中的概率和适应度的值有关,个体适应度越大,被选中的概率越大[14]。 3.4.2 交叉 改进遗传算法采取双切点交叉法。在父代染色体中随机选择两个切点,对其中的片段进行交换,对未交换的染色体片段以部分映射的方式消除冲突,以发货点染色体为例,交叉示范如图5。 图5 染色体交叉 3.4.3 变异 图6 染色体变异 染色体变异能够辅助产生新个体,有助于提高局部搜素能力,同时保持种群的多样性。改进遗传算法采用逆转变异法[15],在染色体集货车部分随机选取2个变异点,将父代染色体中的基因互换,生成下一代染色体。如图6所示。需要进行基因修复。首先,在交叉时,若交换的染色体片段是“0”基因位,则需要重新生成切点,在变异时,如出现交换两基因位相同,重新生成交换位置。其次,需要判段染色体片段是否满足假设条件(3),若不满足,将集货车承载范围外的发货点拥有的货物分配给其他集货车辆。 考虑最近邻算法生成的路径的基因总体表现较为优良,可遗传算法则是具有较高的并行性。由此,本文通过结合最近邻和禁忌搜索思想的遗传算法来解决无水港运输路径优化问题。改进遗传算法的流程如下显示,算法流程如图7所示。 图7 改进遗传算法流程图 步骤1将种群规模设定为N,交叉概率为c,变异概率为v,选择概率是s,和随机概率r,并设定算法终止条件r=Iteration,置进化代数r=0,禁忌表t。 步骤2随机选择一个发货点,由最近邻算法所生成路径的集合设为P,与此同时计算个体的适应度值,并从集合P中随机选择N个初始化第一代种群S(r)。 步骤3及时更新禁忌表t,并将已经搜索过的路径储存在其中。 步骤4在种群S(r)中比较适应度函数,从中寻优选择部分个体作为父代F。 步骤5交叉操作后产生新的路径S1,此路径不与禁忌表中的以往路径重复。 步骤6变异操作后产生新的路径S2,且不与禁忌表中的历史路径重合。 步骤7更新父代和子代的并集Srecent(r)。 步骤8引入新的个体,然后随机生成新的路径S*(r),与禁忌表中的以往路径不相重复。 步骤9 r←r+1,在Srecent(r)⋃S*(r)中寻优选择N个个体作为新的种群S(r)。 步骤10如果满足所有条件,则停止运行并且输出最优值 f,否则返回步骤3。 经过交叉、变异操作后,对于不满足约束的染色体, 与上海港合作的昆山无水港要进行货物收集,昆山港附近有20个发货点,发货点的坐标储存于一个元胞矩阵XY中,每个发货点的发货量储存于元胞矩阵A中,将每辆车的最大载重设定为1 400 kg。 相应的发货点位置,发货量如表1所示。 表1 发货点坐标及发货量 如图8所示,首先构造极坐标系,逆时针旋转极轴,以车辆承载量1 400 kg为约束条件,进行分组处理。如图9所示,通过扫描法,将20个发出点分成了三个区域,每个区域内的发出总量不超过1 400 kg,需要使用3辆货车进行装载。 图8 建立极坐标系 4.3.1 小规模实验 在此案例分析中,使用MATLAB对该路径优化进行模拟仿真。进行实验的计算机配置为Win10 64位操作系统,安装内存(4.00 GB),CPU频率1.80 GHz,所得出的有关运行时间等的数据,都与该机器有关。 图9 货物分区示意图 实验具体参数设置如下,种群规模数量为120,算法终止条件Iteration=400,交叉概率为0.9,变异概率为0.02,同时车辆超载的惩罚权重为300。 对发货点优先级以及车辆运输约束如表2所示。 表2 优先级与运输约束 在满足各种约束的情况下得到无水港集货运输路径优化过程中距离的大小与迭代次数变化的仿真数据如表3。路径优化收敛图如图10,当迭代次数在149次之后,路径优化值没有发生改变,在迭代次数达到400时,算法终止。 表3 模拟仿真数据 图10 运输路径优化收敛图 从表3中可以看出,当迭代次数为149时,最短路径显示为552.37 km,并且,随着迭代次数的延伸,最短路径并未发生改变。最优路径如图11所示。 同时,为了验证改进遗传算法(IGA)的有效性和优越性,将其与传统遗传算法(GA)以及粒子群算法(PSO)进行比较,采用相同的实验数据,并将三种算法参数设置基本一致,对比结果如表4所示。 表4 路径优化结果对比 图11 配送路径示意图 从表4可以看出,在同等条件下,本文所采用的改进遗传算法在较少的迭代次数下迅速得到比遗传算法以及粒子群算法明显更优的解,充分说明本文算法的有效性。 对一区而言,使用改进遗传算法进行路径优化得到的最优路径全长为199.61 km;二区的最优路径全长为168.79 km;三区的最优路径全长为183.97 km。三辆汽车总的行驶距离为552.37 km。 由图11可看出: 第一辆货车: 昆山无水港→发货点14→发货点13→发货点17→发货点15→发货点3→发货点2→发货点18→昆山无水港 第二辆货车: 昆山无水港→发货点5→发货点19→发货点10→发货点4→发货点1→发货点9→昆山无水港 第三辆货车: 昆山无水港→发货点20→发货点7→发货点8→发货点11→发货点12→发货点16→发货点6→昆山无水港 4.3.2 大规模实验 围绕1个无水港进行货物收集,本次实验设置发货点数量为50个,各点货物总质量为9 650 kg,采取小规模实验中相同的集货方式,可以得到在发货点增多时车辆配送轨迹,如表5所示。 表5 大规模实验车辆配送表 4.3.3 多规模实验下的算法对比 在集货运输发货点数量N以及运输车辆数m规模不同时,比较改进遗传算法(IGA)、传统遗传算法(GA)以及粒子群算法(PSO)在运行结果以及运行时间上的优劣性,如表6所示。 对比表6结果可知,在小规模情景中,改进遗传算法下的最优解略好于遗传算法以及粒子群算法,但得到解的速率远大于二者。在实验规模的不断扩大下,从运行时间以及计算结果双重对比下,改进遗传算法的优越性都得到充分体现。综上所述,改进遗传算法能更好地解决本文所提出的问题模型。 以文中使用的小规模实验数据作为依据,用两种传统运输方式与本文改进集货方式运输之后的结果进行对比分析,比较三种方式在运送成本方面的优劣性。 假定每辆车固定成本为1 000元/天,每辆车的变动成本为1.5元/(天·km)。传统无水港集货方式采取点到点集货,就本文而言,集货方式如图12所示。使用MATLAB编程可以求得所有货车行驶的总路程为1 659.74 km,需要使用20辆货车。 表6 多规模实验结果算法对比 图12 传统集货方式 成本计算方法为式(13): 使用传统方式集货的货车数量m=20,总行驶距离L=1 659.74 km,所得总成本C总=69 792.2元 。 因为发货点都会就近选择无水港,所以距无水港的距离都不会太远,所以托运单价稳定。根据市场调研发现托运单价均价为3元/kg。托运总价格计算方法由式(14)给出: 由各发货点货物总质量以及上式可得托运总成本为12 120元。 针对本文所提出的问题,经过研究后得出需要三辆货车即可满足20个发货点所有货物的运输,并且通过改进的遗传算法得出最优行驶路径为552.37 km,根据式(13),可以得出C总=5 485.67元 。将三种运输方式进行对比,如表7。 表7 三种运输结果对比 针对无水港的集货效率低、成本高等问题,提出了一种切实可行的解决办法,即通过共享车辆的形式,既降低了发货商的成本,也使得无水港的管理更加便捷。 通过使用扫描法,在不超过车辆最大载重限额的约束下,将发货点进行分组安排。其次使用改进的遗传算法进行组内路径优化,并用遗传算法以及粒子群算法对不同规模的集货运输进行分析与之对比,得到最优的调度策略,突出改进遗传算法的有效性和优越性。通过Matlab进行数学模拟实验,最终得到改进后车辆需求总数为3辆,配送总成本为5 485.67元,将结果与两种传统方式比较,得出了比自有车辆运输节省92.14%成本,比办理托运节省了54.74%成本的结论,从而证明了本文中所述的方法是更优的。 同时,在本文的研究中未考虑客户对货物配送时间以及满意度的限制,在之后的研究中可以增加约束。另外,针对近几年兴起的城际拼车运输模式,对其最优路径的研究也不失为一条好的思路。



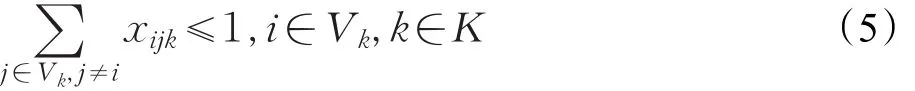
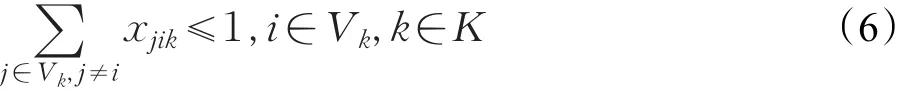



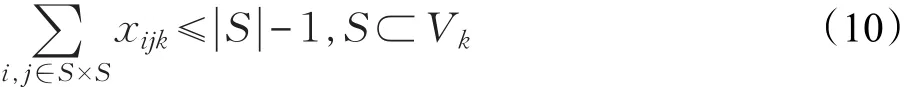
3 改进遗传算法
3.1 染色体编码

3.2 种群初始化

3.3 适应度函数


3.4 种群选择策略


3.6 改进遗传算法流程

3.5 基因修复
4 案例研究
4.1 实验设置
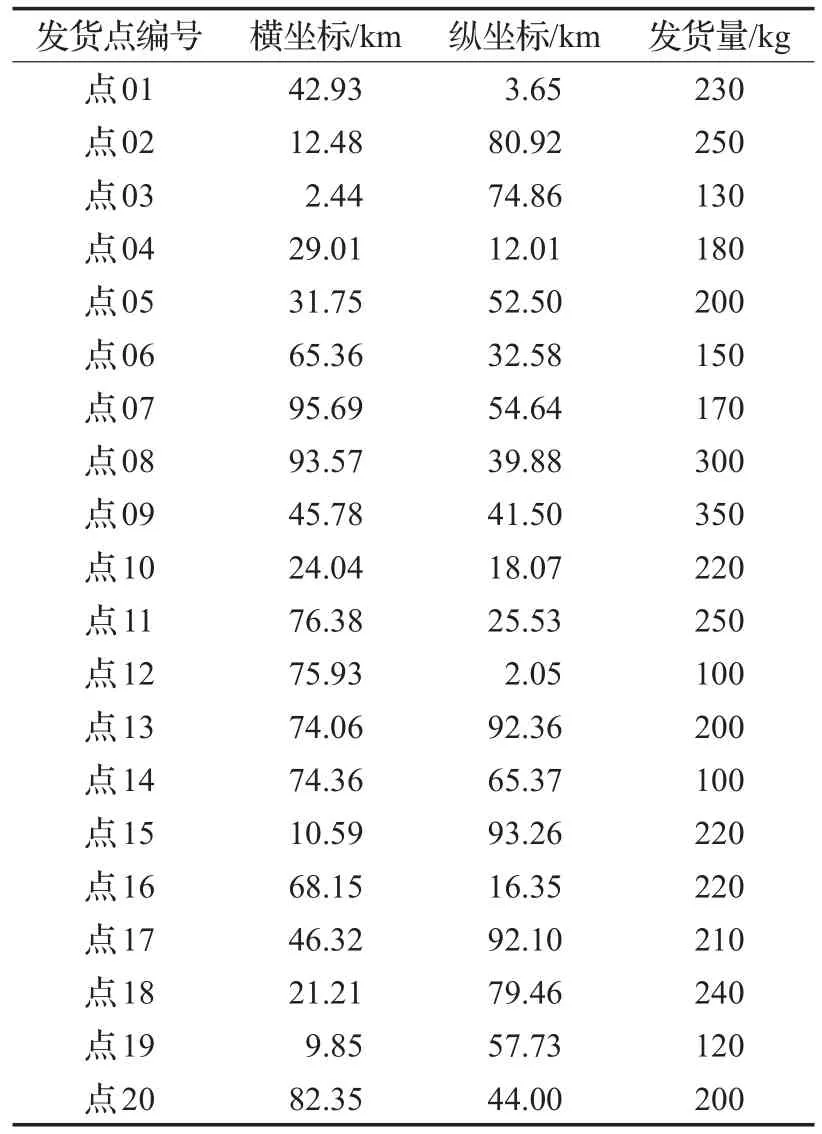
4.2 扫描法分组

4.3 算法参数及实验结果

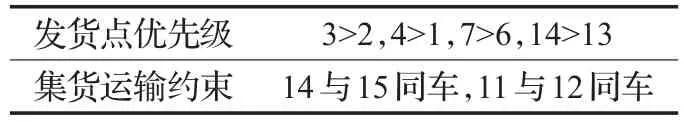



5 结果对比
5.1 货主自有卡车运输



5.2 托运方式运输

5.3 改进后运输方式
6 结语
