基于支持向量机集成的个人信用评估研究
2020-07-17刘潇雅王应明
刘潇雅,王应明
福州大学 经济与管理学院,福州 350116
1 引言
随着国民生活水平的提高,人们的消费心理与消费观念发生翻天覆地的变化,包括个人消费贷款、个人住房贷款、信用卡等在内的个人信贷业务逐渐成为了商业银行的一个重要的利润增长点[1]。信用评估是指根据客户的若干原始资料,通过综合考察影响客户及其家庭的内外客观、微观环境,使用严谨的分析方法,将其分为正常类和违约类,或给出一个违约概率或信用等级[2]。
除了早期通过分析员阅读个人资料决定信用的好坏这种主观性非常强的方法之外[3],传统用于信用评估的主要是统计学方法比如判别分析[4]、logistic回归[5]等,这些方法虽然简单,但在处理非线性问题时效果较差。经过几十年的发展,大量人工智能方法被用于信用评估领域,例如神经网络[6]、k-近邻判别分析[7]等,但这些方法多数基于传统统计学理论建模,依赖海量数据并且容易出现过学习现象[8]。支持向量机(Supoort Vector Machine,SVM)在解决小样本、非线性识别问题中表现出许多独特优势,且基于统计学习理论,具有很强的泛化推广能力,近年来成为信用评估的重要方法。肖文兵等[9]将支持向量机用于信用评估领域并在交叉验证中寻找核函数最优参数,提高分类准确率。肖智等[10]利用支持向量机建立了大学生助学贷款个人信用评价分析模型,通过实证体现了支持向量机方法在分类问题中的优越性。Abedin等[11]利用支持向量机工具对个人信用评估结果预测,并与神经网络模型做了比较,实验验证了SVM泛化能力强、鲁棒性好的优点。
一般认为集成模型可以综合单个分类器的优点,分类效果更好,所以在单一支持向量机研究的基础上发展了支持向量机的集成方法。陈云等[12]将随机子集模型和AdaBoost两种集成策略合成,提出SVM混合集成策略模型用于信用评估,提高了分类的准确率。吴冲等[13]建立了基于模糊积分的支持向量机集成方法,综合考虑每个子分类器输出的重要性,并对商业银行的信用风险进行评估,通过实证分析得出了集成方法分类精度更高的结论。夏国斌[14]使用Bagging算法集成支持向量机信用评估结果,并与传统判别分析与逻辑回归做了比较。然而这些集成方法均没有考虑到基分类器对分类结果的判断能力的差异性和可靠性这一问题。
证据理论在不确定性信息表达和合成方面优势突出,因此在融合不确定性结果中得到了广泛的应用。但是基分类器的判断结果相互冲突时,DS证据理论会得出与直观相悖的结论。基于此,本文提出基于改进DS证据理论的支持向量机集成个人信用评估方法。利用SVM的后验概率,混淆矩阵和类别标签构造DS证据理论概率赋值函数。对于冲突结果,计算分类器间支持度的权重和专家权重对分类器赋权,区分可信度并修正冲突。除此外,模型训练之前,利用C4.5决策树信息熵增益率理论,约减冗余属性,提高模型整体效率。实验部分,使用UCI公开信用数据检验模型效果,结果表明,集成方法比单一模型分类效果更好,本文集成模型较于其他集成模型可以取得更高的预测精度,具有良好的现实意义和应用前景。
2 DS证据理论组合规则
证据理论最早由Dempster提出[15],后来他的学生Shafer将理论进行了完善。对于某类判决问题,用一个完备集合Θ表示其所有的可能结果,如果集合中元素之间是两两互斥的,称这个完备集合Θ为辨识框架。如果集函数m:2Θ→[ ]0,1满足:

设m1和m2是两个独立的基本概率赋值,组合之后的基本概率赋值m=m1⊕m2(⊕是正交和)。设BEL1和BEL2是同一辨识框架的两个信任函数,m1和m2分别是对应的基本概率赋值,焦元分别是A1,A2,…,Ak和 B1,B2,…,Br。
DS的组合规则如下[16]:
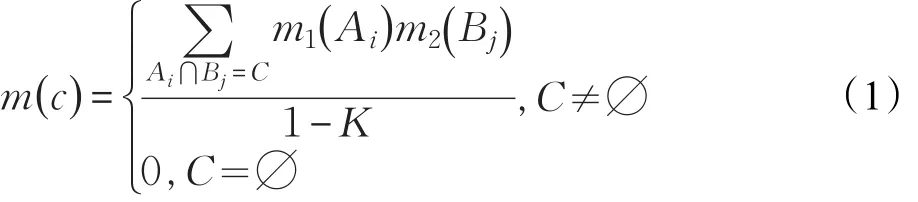
其中,K是冲突因子,反映了证据之间的冲突程度。

由式(1)可以看出,当K等于1时证据理论的合成规则显然不再适用。
3 基于支持向量机的基本概率赋值
DS证据理论中,基本概率赋值函数(BPA)往往难以确定,本文将SVM与DS证据理论结合实现基本概率赋权。大致思路为:首先得到SVM的后验概率输出,作为初步的判别结果;其次通过混淆矩阵得到真实类别和预测结果之间的关系作为局部可信度估计值;然后将局部可信度加权融合到后验概率中作为基本概率值。
3.1 SVM后验概率输出
使用证据理论对SVM集成时需要知道SVM预测样本输出的概率值,因此需要将传统SVM输出的类别标签转化为概率软输出。sigmoid函数可以将支持向量机输出结果转化为后验概率输出[17-18],具体方式如下:

f是标准SVM输出结果,A和B是函数中的参数值,可以通过求解参数集合的最小负对数似然值而得:

3.2 基于混淆矩阵的可信度计算
假定类别数为k的分类问题,利用分类器l分类后所得到的混淆矩阵表示形式如下:


将分类器l的局部可信度记为PCl(wi),它表示当前的样本属于类别i的一种支持度,即对分类器局部的一种信任程度。
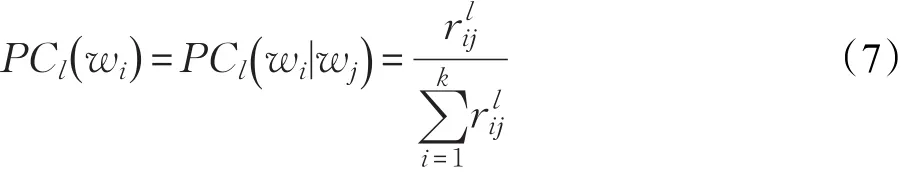
将其融入到支持向量机的概率型判别输出Pi之中可得:

ml(wi)即表示分类器l对样本x属于某类i的概率赋值即BPA。
4 基于改进DS证据理论的SVM集成个人信用评估模型
信用评估问题中,单个分类器的判别准确性往往也有限,且可能会出现泛化不佳的问题。组合多个分类器得到一个综合的结果的集成模型,已经成为了提高信用评估分类问题准确率和稳定性的一个有效的手段。各基分类器的输出都具有一定的不确定性,对于这些不确定性信息的集成过程也是一个不确定的推理过程。本文个人信用评估模型采用了集成方法,对DS证据理论处理冲突问题时的缺陷进行了改进,考虑基于证据间支持度的权值ρ和样本分类精度λ并依此对分类器赋权,同时考虑属性约减,提高模型训练效率。
整体思想为:首先利用C4.5决策树计算数据集属性贡献率,依据贡献率大小约减属性减少冗余;其次利用SVM构造DS证据理论的概率赋值函数BPA;然后检验结果是否有冲突,对冲突证据赋权;最后用DS证据理论融合规则对SVM集成完成最终决策。
4.1 DS证据理论冲突改进方法
由式(1)可知,当冲突因子K=1或者趋近于1时,显然证据理论合成规则不再适用,如果继续合成会出现与事实不符的结果。基于此,本文对冲突证据进行了改进。
假设信用评估系统有l个SVM分类器,识别框架含有N个命题,H是识别框架的任意子集。mi(i=1,2,…,j,…,l)是基本概率赋值:

相互独立的证据体之间的夹角余弦可以用如下形式来表示[19]:

由余弦定理可知,夹角的余弦值为1时,表明两个证据完全重合,没有差异。随着夹角的增大,余弦值越来越小,到90°时,余弦值为0,两证据不相关。因此,可以用夹角余弦值表示证据之间的相似程度,它的值越小表明判别结果之间的相似度越低,证据越冲突,越大表明相似度越高。式(10)计算出的相似度值用矩阵形式表示如下:

相似矩阵行和定义为证据间的支持度,用Supi表示,支持度越高表明某个证据越为可靠,应该赋予的权重越大。以ρ表示平均支持度并作为基于证据间支持度的权重:

分类器本身分类准确率是衡量其性能最直观的指标,因此本文还考虑了样本在测试集上的预测准确率λ作为专家权重修正基于支持度的权重。基分类器的分类准确率越高说明其可靠性越强,应该给予的权值越大。均衡考虑分类器间差异与分类器自身分类效果优劣,定义总权重γ为:

依据总权重对基分类器的基本概率分配函数加权,即可改进在DS融合过程中可能出现的证据冲突问题。
4.2 基于改进DS证据理论的SVM集成个人信用评估模型
基于改进DS证据理论和SVM的个人信用评估集成模型如图1所示,具体步骤如下:
步骤1 C4.5决策树约简属性。C4.5决策树以信息熵增益率方法测试属性,克服了传统算法中属性选择偏向于选择取值多的属性的缺点。具体步骤有:
(1)设置损失比例。信用评估的实际问题中,将信用“好”的客户误判为信用“差”的客户损失的可能仅仅是贷款利息,而将信用“差”的客户误判为信用“好”的客户则可能遭受巨大的违约风险,二者所造成的损失不对等,决策树模型设置损失比例将可能导致的损失引入系统的分析过程。
(2)训练最优树。对现有样本迭代,增大误判样本被抽为训练集的可能性,提高模型精度。确定决策树的修剪严重性,生成最优树。

图1 改进DS证据理论的SVM集成模型
(3)计算属性贡献率。依据信息熵增益率原理,计算最优树下属性对分类结果贡献率,约减冗余属性。
步骤2训练SVM基分类器。
步骤3计算SVM后验概率及局部可信度。
步骤4利用SVM结果合成基本概率赋值函数。
步骤5若证据间存在冲突,计算基于支持度的权值ρ和基于分类准确率的权值λ,并合成最终分类器权值γ,对分类器的可信赖程度加以区分。
步骤6用DS证据理论做SVM的结果集成,并输出最终判决。
5 实证分析
5.1 数据集介绍及属性约减
实验选取UCI机器学习库的两组真实公开信贷数据进行模型效果验证,分别为德国信贷数据和澳大利亚信贷数据。数据集描述如表1,考虑样本数值相差较大,实验之前已对其归一化处理,德国信贷数据属性具体描述如表2所示。
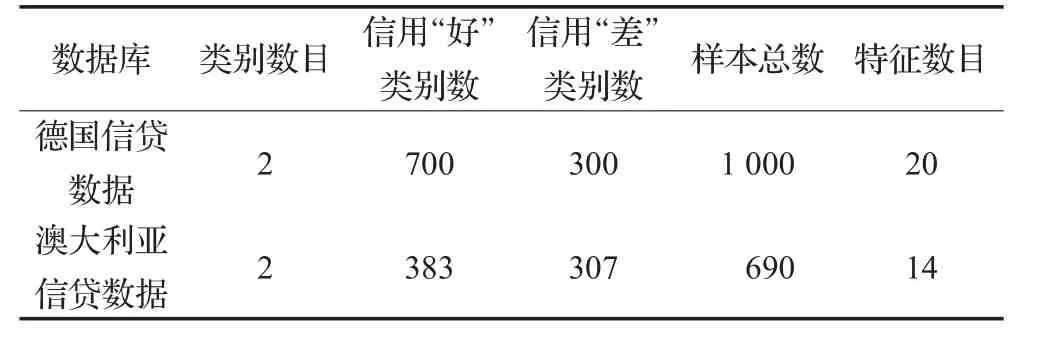
表1 数据集描述
依托clementine12.0平台,对数据集5折交叉验证:实验结果表明按损失比例2∶1,Boosting迭代次数10,修剪严重性85可生成德国数据集的最优树,各个属性贡献率如图2所示。按损失比例2∶1,Boosting迭代次数10,修剪严重性65生成澳大利亚数据集最优树,各个属性贡献率如图3所示。
选取对于分类结果贡献率不为零的属性,除去类别标签德国数据集由24维约减为12维:变量1(0.263 4)、变量4(0.147 8)、变量2(0.135 2)、变量3(0.122 6)、变量17(0.112 2)、变量5(0.076)、变量10(0.063 1)、变量21(0.044 1)、变量 13(0.02)、变量 24(0.009 4)、变量 20(0.005 4)、变量16(0.000 8);澳大利亚数据集由14维约减为 9维:属性 8(0.767 8)、属性5(0.054 2)、属性 3(0.052)、属性 2(0.033 2)、属性 9(0.032 6)、属性 14(0.009 1)、属性12(0.007 7)、属性7(0.004 3)、属性11(0.002 5)。

表2 德国信贷数据集描述

图2 德国数据集属性贡献率
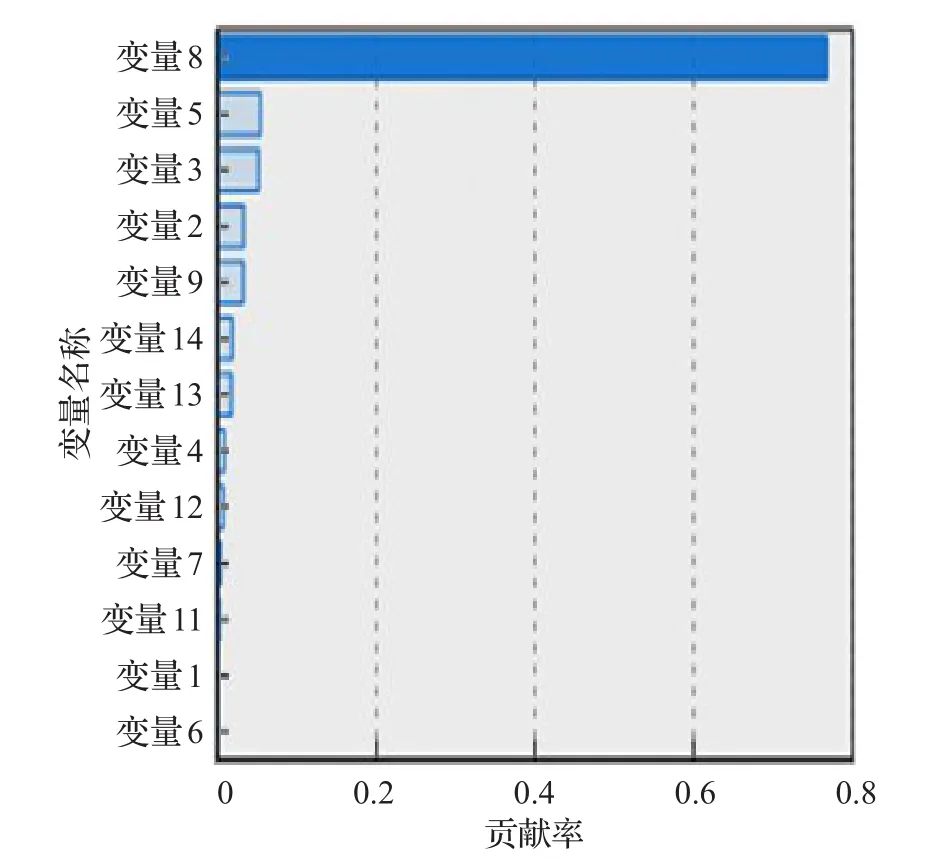
图3 澳大利亚数据集属性贡献率
5.2 实验设计
常见多分类器集成思路有两个,一是将不同形式分类器集成,另一个是使用同形式的不同类型的分类器。本文选择集成方法的第二种,选用三种基于不同核函数的支持向量机作为基分类器,这三种核函数分别为线性核、多项式核和高斯核,分别表示为SVM1、SVM2和SVM3。实验依托Matlab 2016a平台,使用Libsvm工具包,所有的支持向量机最优参数均用网格法通过交叉验证求得。
为验证本文模型效果的优越性,在两组公开数据集上,实验同时与不同核函数支持向量机单一模型、神经网络模型、未改进的DS集成模型(DS-SVM)、基于bagging集成算法的SVM模型(Bagging-SVM)和基于Boosting集成算法的SVM模型(Boosting-SVM)等常见用于信用评估的模型进行了比较。同时为证明属性约减的必要性,将计算结果分为两类:一类是不经过属性约减的情况,称为情况1;另一种是考虑属性约减的情况,称为情况2。
5.3 评价指标
本文选择两个指标来评估模型的效果,分别是F-score和平均准确率(Average),这两个指标可以综合常用于信用评估的precision查准率与recall召回率,根据表3混淆矩阵,指标的计算方法如下:


表3 混淆矩阵
5.4 实验结果及分析
不同分类器得到基于识别率的混淆矩阵表示如下:C11,C12,C13表示情况1下的 SVM1、SVM2、SVM3输出的混淆矩阵,C21,C22,C23表示情况2下SVM1、SVM2、SVM3输出的混淆矩阵。
德国数据集混淆矩阵为:

依据已经得到的混淆矩阵,由公式(7)计算可得两个数据集各分类器可信度值见表4所示。
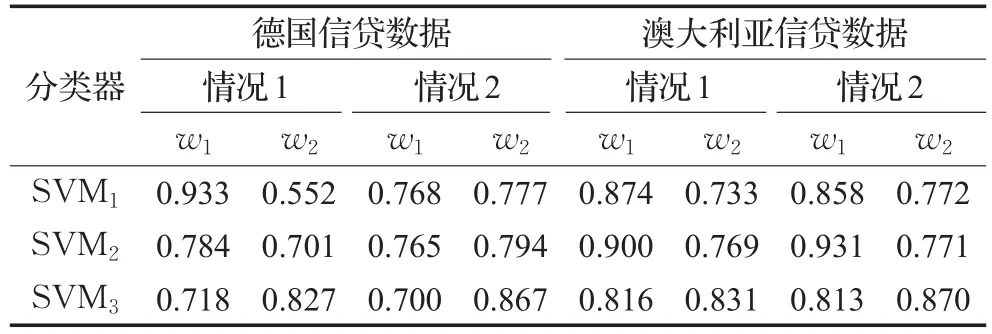
表4 局部可信度
将支持向量机的后验概率,局部可信度利用式(8)合成概率分配函数(BPA),并按照4.2节内容计算权值λ和ρ同时合成最终赋权权值γ。测试样本集成后分类结果和对比模型结果见表5和表6。
通过实验从表5、表6中可以得到如下结论:
(1)比较七个模型属性约减前后评价指标大小可知,在两个测试数据集上,情况2各分类器的平均准确率和F评分均高于情况1。以澳大利亚数据集SVM3为例,在属性约简前F评分为0.810,平均准确率为78.4%;属性约减后F评分为0.853,平均准确率为83.8%,F评分提升了0.043,平均准确率提升了5.4个百分点,说明非重要属性的减少不会影响模型的精度,反而减少冗余属性可以优化支持向量机受无关维度影响导致准确率下降的缺陷,从而提升模型效果。
(2)两组实验中,集成模型F评分和准确率明显优于各个单一支持向量机分类器,说明了集成方法的优越性。本文提出的改进DS证据理论集成方法,充分利用了SVM输出的所有信息,将对分类有用的类别标签、后验概率、混淆矩阵都进行了融合,同时改进了冲突证据引起的决策失误,对分类器加权区分可信度,性能更明显高于单一的模型和普通DS证据理论集成方法,在测试集上准确率可达90%左右。

表5 德国数据集实证结果
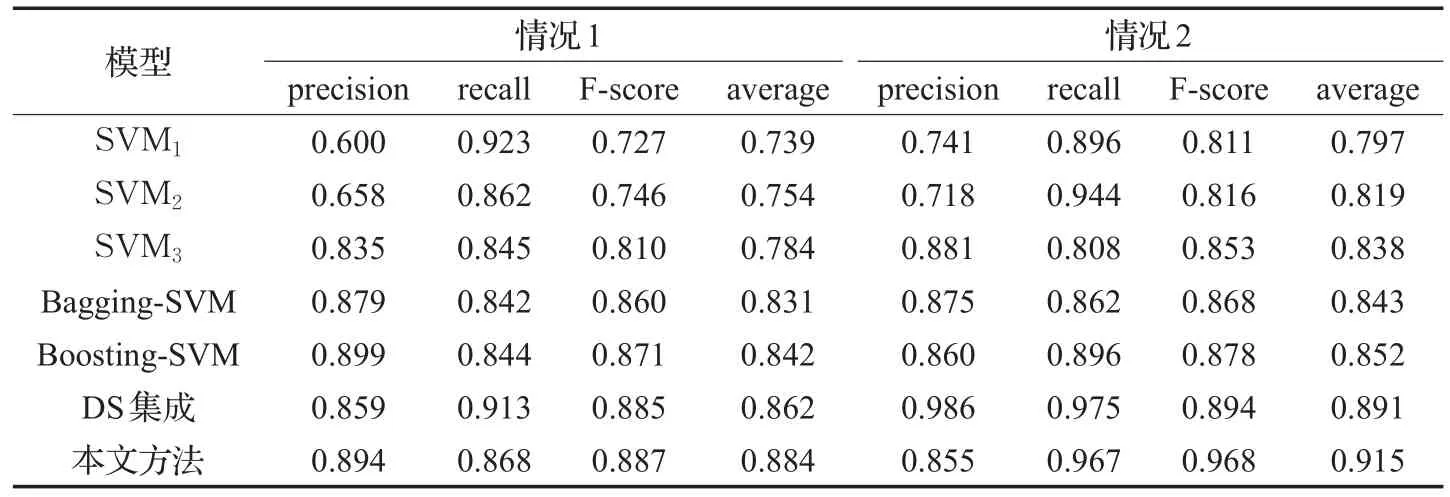
表6 澳大利亚信贷数据集
(3)基于改进DS证据理论的SVM集成方法,属性约减前后F评分值和平均准确率均高于Bagging-SVM集成、Boosting-SVM集成方法和普通DS-SVM。说明本文提出的集成模型实用、有效,充分考虑分类器差异性,且改进冲突证据对提升模型准确率有明显效果。
用柱状图直观比较不同核函数预测精度,如图4,图5所示。从图中可以看出情况2精度均明显高于情况1,面向高维多样本信用评估数据时,高斯核函数分类精度最佳,其次是多项式核函数,最后是线性核函数。高斯核函数由于参数较多项式函数少,计算复杂度低,且比线性核函数更适合处理多维数据,所以是信用评估方面最优的核函数选择。
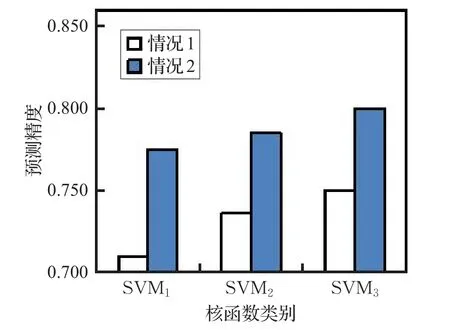
图4 德国数据集核函数比较
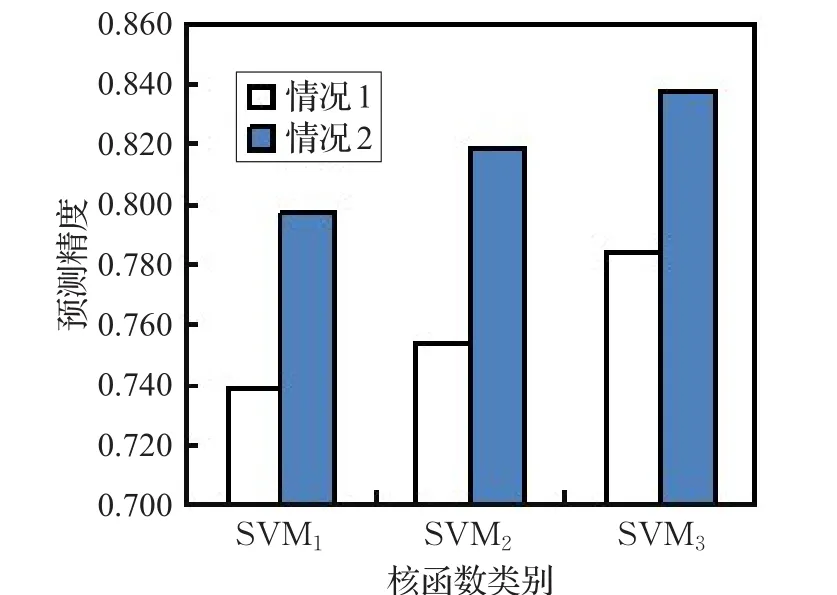
图5 澳大利亚数据集核函数比较
6 总结与展望
在信贷消费日益普及的高速信息化社会,个人信用评估的研究意义越来越重要,信用评估方法的好坏直接影响了信贷消费的走向健康与否,分类精度哪怕1%的提升都会挽回金融机构数以万计的损失。在此背景下,本文提出了一种基于改进DS证据理论的支持向量机集成个人信用评估算法,并且考虑了冗余属性对分类结果的影响,将属性约减这一因素纳入模型中。该模型优点是不仅集成了分类器达到了较好分类效果且有更强的“鲁棒性”,并且利用数据集实际分类信息构造基本概率分配函数使得概率赋值更加可靠,同时修正了冲突证据造成的分类误差,较单一SVM模型和传统集成方法效能明显提高,具有很好的泛化能力,说明此模型用于个人信用评估是可行和有效的。
未来进一步研究方向:(1)如何在保证精度的前提下将改进模型用于多分类情况中值得进一步思考。(2)本文的子分类器使用了三种不同核函数的分类器,以后可以考虑将不同类型的分类器组合集成,例如SVM、神经网络、决策树。
