全变分的叠加迭代降噪算法的研究

颜 鼎，吕东澔，张 勇

内蒙古科技大学 信息工程学院，内蒙古 包头 014010

1 引言

随着科技的飞速发展，信号的准确性在实际应用中变得越来越重要，设备采集到的原始信号必然夹杂着一定的噪声，这些噪声会对后期的信号分析和处理造成干扰。因此，提升信号降噪的准确性是非常有必要的，这也是当今的研究热点。傅里叶分析、小波阈值、聚类分析、经验模态分解等降噪方法目前应用广泛，但是对于稀疏信号的降噪，这些算法会造成有效信号的幅值丢失。全变分降噪算法（Total Variation Denoising，TVD）能够对稀疏信号进行有效降噪而且应用广泛，针对全变分降噪中构建目标函数求取最小值的问题，Selesnick I W等人提出了关于该问题的不同算法，例如Majorization-Minimum（MM）算法[1]，有效地利用优化-最小值的算法找到噪音中的最小值点，但对峰峰值大范围跳变的稀疏信号进行降噪会产生较大的误差。Soft算法[2]整体能够实现信号的降噪，但降噪后的信号幅值会丢失准确性。文献[3]针对参数罚函数，对罚函数的参数进行约束，以保证目标函数的凸性。但降噪后原信号的框架会有所丢失。Graber H L等人[4]对文献[1]进行改进，提出了采用离散时间滤波器对MM算法进行改善，提升了算法效率，节省了大量时间。在信号平滑性的改善中。文献[5]提出的算法，把降噪后的信号变得更加平滑，文献[6]提出了一种新的小波变换算法对信号降噪，高效地提高了降噪信号的准确性。文献[7]联系了文献[2]与文献[4]中的算法，对一范数进行准确估计，这样不仅能减少噪声的影响，同时还能够保存目标函数的原特性。Wu K等[8]结合了MM算法与POB算法，提出了MM-POB算法，有着较强的实用性。刘盈娣等[9]介绍了基于曲率差分的全变分降噪算法，极大平滑了信号边缘的原始信号，文献[10-15]解决了分数阶全变分和全变分模态的优化问题。

本文提出的基于全变分的叠加迭代降噪算法在TVD算法的基础上进行了改进，通过对原信号的差分和叠加形成新的信号，对该信号再进行TVD算法的滤波降噪，极大地抑制了噪声对信号的干扰。通过该算法降噪后的信号与原始信号框架更加接近，而且提升了信号幅值的准确性。

2 TVD降噪原理

TVD算法在降噪领域里应用广泛，该方法的具体思路是把需要降噪的信号的目标函数构建成一个凹函数，对这个凹函数进行求导，找到凹函数的最小值，这个最小值就是利用全变分降噪方式后的降噪后的信号[2]。

λ为惩罚项的系数。可构建目标函数：

式中，y∈RN，λ>0。

由于目标函数J(x)为凹函数，所以能够被迭代求解出最小值，该最小值即为降噪后的信号。Nit为需要迭代的次数。TVD算法可以简写成：

TVD算法步骤可总结如下：

（1）设置n=1，选择 λ>0。

（2）对TVD构建的目标函数J(x)求微分。

（3）目标函数中对二范数求微分可求，但由于对一范数求微分存在多种不同情况，故可设计不同算法公式来解决这一问题。

5.根据对假设五检验得出的结论，笔者认为，除了相关准则要完善对企业无形资产研发支出资本化的规定，会计师事务所在对企业进行审计时，也要更加注意该方面内容的审计，重视报表附注对开发支出的披露，尤其是对报表附注披露不规范的情况实施相应的审计程序，从第三方角度进行监督管理，以避免企业利用准则的漏洞做出一些违规舞弊行为，扰乱经济秩序，误导报表使用者做出错误判断。

（4）令目标函数微分后的公式为零求得对应最小值的X，该X即为所要求的降噪后的信号。

（5）n=n+1。

（6）返回步骤（2），依次迭代，直到出现信号最准确的代数为止。

3 本文算法

为了更好地消除噪音对信号的影响，基于TVD算法和MM算法的各自优点，提出了一种新的降噪算法，其基本思想如下：

首先对原信号y进行TVD降噪，求得第一次降噪后的信号x1，如下式表示：

再对x1进行TVD方式降噪得：

随后用第一次降噪获得的信号与第二次降噪获得的信号相减，保留了连续两次TVD降噪后的信号框架，得到一个新的信号β。

其中，0<α<1,α的数值是根据本文算法所迭代的次数进行定义的，具体数值为迭代次数的倒数，通过改变α的数值来使本文算法对迭代次数有更低的敏感度，以此来提高本文算法的消噪鲁棒性，把β进行α倍的缩小，再和原信号相加得到y1。得到的y1不仅包含着原始的y信号，并且还含有连续两次对原始信号的降噪后的结果，得到的新的信号更具有这两方面的特点，降噪效果更接近原始信号。

再对y1进行TVD方式的连续迭代降噪。迭代次数为Nit，降噪到信号出现最准确的代数为止：

上述过程的目的是使TVD算法求得的信号每次迭代都进一步地接近理想信号。每次求得的新信号，不仅含有原始信号的信息，而且含有连续两次TVD降噪后的信号的信息。每次迭代后都能在原TVD信号降噪的基础上接近有效信号。该算法降噪后信号的准确性优于TVD算法。

本文算法步骤可总结如下：

（1）设置n=1:Nit，其中Nit为需要迭代的次数。

（2）对原始信号进行第一次迭代降噪：x1=tvd(y,lam,1)。

（3）对第一次TVD降噪后的信号再次进行TVD降噪：x2=tvd(x1,lam,1)。

（4）对两次TVD降噪后的信号和原始信号进行按比例相结合，求得新信号y1:y1=y+α[x1-x2]。

（5）再对y1进行多次迭代降噪xn=tvd(y1,lam,Nit)。

（6）n=n+1。

（7）返回步骤（2），依次反复迭代，直到出现信号最准确的代数为止，把本文最优降噪迭代的次数设置为Nit。

4 数据分析及实验结果

本文实验数据分为A组、B组，两组信号的原始稀疏信号相同，噪声信号不同。其中A组采用文献[1]中的含噪信号，B组采用均值为0，方差为1的随机噪声信号。使用MM算法、Soft算法和本文算法对两组信号进行降噪，实验结果如下：

从A组实验结果可以看到，本文算法的降噪效果明显优于MM算法和Soft算法。图1中的实验数据表明：本文算法能够有效地保留原始信号的框架，实现了对峰峰值区间内噪声的抑制。

图1 三种不同算法对A组信号降噪效果比较

图2 的实验结果表明：在迭代次数上，Soft算法随着迭代次数的增加，目标函数不断增加，降噪效果变差，故首次迭代则为最优解，如图1中Soft算法所示。MM算法与本文算法随着迭代次数的增加，目标函数趋于最小值。由于本文算法具有保持原始信号框架的优点，故采用本文算法的目标函数最小值优于MM算法和Soft算法，明显提升了降噪效果。

图2 三种不同算法对A组信号目标函数的收敛比较

从图3和表1的实验数据整理中也可以发现：本文算法降噪后的误差明显小于MM算法和Soft算法。

图3 三种不同算法对A组信号降噪后的误差分布

表1 三种不同算法对A组信号降噪后误差指标对比

根据A组的实验结果，与MM算法和Soft算法相比，本文算法降噪后信号的准确性得到了显著的提高，更加接近原始信号。

B组实验的目的是为了通过对随机噪声的有效抑制，表明本文算法更广泛的适用性。实验结果如图4、图5所示。

从B组的实验结果可以发现：采用MM算法和Soft算法进行降噪后的信号和原始信号相比，在随机扰动的信号中依然无法解决对稀疏信号大范围跳变的点的有效降噪。根据图6与表2的实验数据中可以表明采用本文算法有效地实现了对带有随机噪声干扰的稀疏信号的降噪，更多地保留了原始信号的细节。从目标函数的最优值和降噪后信号误差的分布两方面的比较都体现出了本文算法的优势。

本文算法应用于针对峰峰值大范围跳变的稀疏信号降噪问题中，从表3的分析数据可得，原始仿真信号的正向信号平均值与负向平均值相加远远小于原始信号峰峰值，由此可得原始仿真信号为峰峰值大范围波动的信号。

图4 三种不同算法对B组信号降噪效果比较

对同一含噪信号分别使用MM算法、Soft算法、本文算法进行去噪，通过改变迭代次数，比较降噪后的实验结果，总结各算法消噪的鲁棒性。由图2、图5可看出，随着迭代次数增加，Soft算法的降噪效果变差，MM算法与本文算法的降噪效果变好，且本文算法的降噪效果更好于MM算法。通过以上实验结果说明了本文算法的鲁棒性优于MM算法与Soft算法。

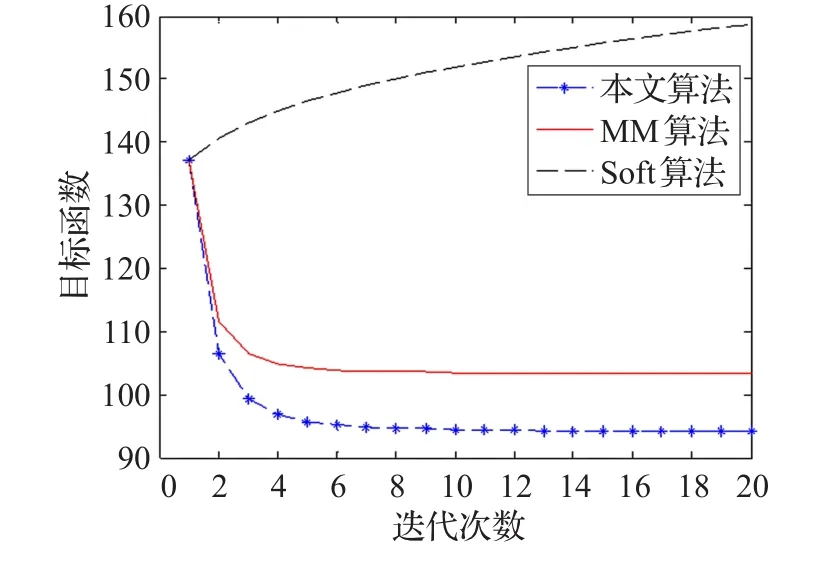
图5 三种不同算法对B组信号目标函数的收敛比较

图6 三种不同算法对B组信号降噪后的误差分布

表2 三种不同算法对B组信号降噪后误差指标对比

表3 原始仿真信号各指标

在实际采样中，高电压脉冲下，生物组织的电流信号与电压信号，均为方波信号，求导后信号值为零，通过判断零信号和求导后的零信号占总体信号一半以上，这样确定的信号是稀疏的。图7与图8为实际工程中的电压信号与电流信号，与本文所滤波的信号相匹配，均为稀疏信号。

图7 降噪前的电流信号

图8 降噪前的电压信号

图9 与图10实验结果表明，本文算法在实际应用中效果显著，保留了原信号中的基础框架，对噪声进行了有效滤除。在对实际工程的稀疏信号降噪中具有应用价值。

图9 降噪后的电流信号

图10 降噪后的电压信号

5 结束语

本文基于TVD算法提出了一种全变分后叠加迭代的降噪算法，该算法叠加带噪信号和全变分一次迭代降噪信号的信息构建新信号，对新信号进行迭代降噪。通过对既定含噪信号和随机扰动含噪信号的降噪实验可以看出，本文算法能够有效地解决峰峰值大范围跳变的稀疏信号的降噪问题，在保留原始框架的基础上，提升了信号幅值的准确性。