基于IGGIII 方案的自适应渐消卡尔曼滤波器

贺军义，杨 丰，安葳鹏，尚家泽

河南理工大学 计算机科学与技术学院，河南 焦作 454000

1 引言

自适应渐消卡尔曼滤波器（Adaptive Fading Kalman Filter，AFKF）通过引入渐消因子扩大准确量测信息的权重，能在一定程度上抑制模型建立不准确或模型参数突变时标准卡尔曼滤波器（Kalman Filter，KF）容易发散的问题，使滤波精度以及动态性能方面都有了相应的改善[1-3]，但是该方法使用固定长度的滑动采样区间，计算出的渐消因子在不同噪声环境下，滤波调节能力具有单一性，不利于滤波精度的提高。文献[4]提出一种计算多重渐消因子的方法，并根据均方误差把渐消因子分配给各个滤波通道，提高了自适应卡尔曼滤波算法的滤波精度，多重渐消因子的引入使计算量倍增，存在空间复杂度上升和实时性下降的问题。文献[5]对不同滑动采样区间长度采用加权组合思想求取新息协方差估计值，再采用交互多模算法进行信息融合，从而获得精度更高的滤波估计值，但该算法加权计算过程使时间复杂度明显增大，滤波效率严重下降。文献[6]通过构建噪声统计特性检测函数进行量测噪声方差阵的梯度检测，然后根据检测结果利用窗口自适应函数实时计算窗口宽度，避免滑动窗口长度固定带来的滤波精度与跟踪灵敏度之间的矛盾问题，然而该算法梯度检测函数对3组预设量测噪声方差修正系数进行求和运算，再进行加和运算求取最终梯度检测值，影响了算法滤波实时性。文献[7]对开窗估计法求取的协方差阵估计值和通过新息序列推求的协方差阵分别求迹，再将两个迹的值相除直接得到渐消因子，简化了渐消因子的计算过程，使运算效率有所提高，但该算法计算渐消因子时忽略了较小的观测噪声矩阵，造成滤波精度下降。

为解决上述现有算法所存在的问题，本文针对自适应渐消卡尔曼滤波器滑动采样区间长度选取进行了细致研究，提出了一种基于IGG（Institute of Geodesy and Geophysics，Chinese Academy of Sciences）III方案的自适应渐消卡尔曼滤波器（IGGAFKF）。该滤波器首先利用新息马氏距离服从卡方分布作为判断准则进行新息异常检测，然后根据不同检测结果，通过构建一个类似于IGGIII权函数的三段式滑动采样区间长度N的选取表达式，求取不同噪声环境下的滑动采样区间长度。改进滤波算法的滑动采样区间长度为在线求取，能够实现估计精度与动态性之间平衡的同时，兼顾滤波器实时性要求。Matlab仿真验证了基于IGGIII方案的自适应渐消卡尔曼滤波算法的正确性和有效性。

2 自适应渐消卡尔曼滤波器

标准卡尔曼滤波器在线性离散系统下的状态方程和量测方程分别如下[8-10]：

式中，Xk为被估计的状态变量，Zk为量测变量，Ak,k-1为状态转移矩阵，Bk为测量矩阵。Wk和Vk分别为系统噪声和观测噪声，系统噪声Wk已知且量测噪声Vk为方差时变的零均值白噪声，各个时刻噪声未知且互不相关，其方差分别为

标准卡尔曼滤波器算法滤波过程为[13]：

式中，vk为新息，Dk为新息方差，Kk为卡尔曼增益矩阵。

文献[14]提出的渐消卡尔曼滤波器将式（4）中引入渐消因子，即用式（8）代替式（4）：

则式（3）（8）（5）（6）（7）构成了自适应渐消卡尔曼滤波算法。渐消因子λk大于等于1，当计算出的渐消因子变为标准卡尔曼滤波器[15]。实际值小于1时取1，即自适应渐消卡尔曼滤波器：

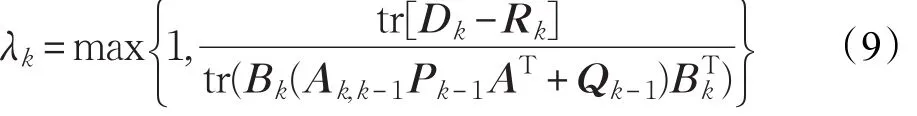
式中，Dk为滑动取值长度为N时的新息方差估计值[16]：

与标准卡尔曼滤波器相比，渐消卡尔曼滤波器通过引入渐消因子使估计均方误差增大为原来的λk倍，进而扩大增益矩阵Kk，增加了新近观测信息所占权重，从而提升算法对准确数据的动态跟踪性能，达到改善滤波精度的目的。

3 基于IGGIII方案的自适应渐消卡尔曼滤波器

自适应渐消卡尔曼滤波算法中渐消因子求解方式存在显著缺点，制约了滤波精度的提高。式（10）利用滑动采样区间内数据进行新息方差的估计时，滑动采样区间长度N难以确定。若选择的N值过大，开窗法求取的新息方差估计偏小，造成渐消因子变小，渐消卡尔曼滤波器估计值更接近于标准卡尔曼估计值，导致滤波器在模型参数发生变化时，对准确观测量的动态跟踪性能下降。若选择的N值过小，在模型稳定情况下使求取的渐消因子变大，增加了滤波器对观测量的动态跟踪性能，但降低了准确一步预测值在滤波结果中的权重，滤波器鲁棒性变差，易导致滤波精度降低。所以，通过不断测试设定的单一固定采样区间长度N无法满足滤波器在不同噪声环境下的滤波需求。实现滑动采样区间长度N的自适应求取，使其适应不同的噪声环境，是提高渐消卡尔曼滤波器滤波精度的根本措施。

3.1 新息异常卡方检测

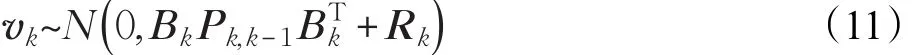
新息vk服从零均值高斯分布，且观测量Zk也服从高斯分布，新息马氏距离的平方应该服从χ2分布[18]：

式中，Mk为马氏距离。

为了检验当前新息vk是否与假设模型兼容，并判别新息vk的可信程度，根据假设检验理论，设置一个显著性水平α：

在新息信息中包含模型信息和观测信息，对新息异常进行检测是采取自适应策略提高滤波精度的前提。新息是一个服从零均值正态分布的白噪声序列[17]，即：波器中观测信息相对准确，那么新息异常由模型或噪声参数不准确引起。因此，采用新息马氏距离服从卡方分布能够有效检测新息是否出现异常，并分析出造成新息异常的原因。式中显著水平α表示新息统计量与假设模型兼容的概率，其大小决定了新息统计量门限值χ2m,α的大小。在实际工程运用中，由于难以精确选取系统噪声，α较为合适的取值范围是0.01～0.15[17]，采用该方法得到进行新息异常划分的具体显著水平α数值可通过实验测得，并不需要在线迭代计算，不会造成滤波效率的大幅下降。

3.2 IGGIII权函数

IGGIII方案是一种类似于相关最小二乘估计的抗差估计方案[20]。该方案将观测数据按照质量划分成有效信息、可用信息以及有害信息。对应权函数中的保权区、降权区、淘汰区。基本实现了对有效信息的充分利用、可疑信息的限制利用以及对有害信息的排除，是一种适合处理量测数据的处理方案。IGGIII的权函数为：

式中， ||ui为标准化残差，k0和k1为调和系数。

3.3 滑动采样区间长度优化选取

利用以上新息卡方检测方法，并引入IGGIII信息分类思想，通过先验经验和实验测试设置显著水平α1、α2。并设原滑动区间取值长度为N，调节因子为κ，且令βk=，则采用IGGIII方案进行自适应优化后的取值长度N̂为：

式中，α1决定滑动采样区间长度取值取最长的几率，决定滤波器的估计精度；α2决定滑动采样区间长度取值最短的几率，决定滤波估计的动态跟踪性能。所以α1取值应该尽量使其对应的门限值偏大，以获取更高的稳定性，α2应该使其对应的门限值偏小，在发生模型参数变化时具有更好的动态性。经过多次实验，本文α1、α2分别设置为0.10和0.01。

当滤波出现发散时，通过滑动区间长度取最短，增加滤波估计值中准确观测信息的权重，使滤波估计值向准确观测值方向收敛。并且通过式（10）可知，滑动区间取最短会使开窗法求取协方差估计值时的求和运算量降至最低，加快协方差估计值求取速度，使滤波结果实现快速收敛，提高滤波精度。

3.4 基于IGGIII方案的自适应渐消卡尔曼滤波器算法

结合新息卡方异常检测和滑动采样区间长度优化选取的内容，本文提出的基于IGGIII方案的自适应渐消卡尔曼滤波器算法工作流程如下：

步骤1 初始化赋值，X0、P0、α1、α2、N 。

步骤2通过式（3）进行一步状态预测。

步骤3求取自适应渐消因子。

步骤3.1求取新息向量：

步骤3.2通过式（15）进行新息卡方检测和求取融入IGGIII方案思想的滑动区间长度。

步骤3.3求取新息方差最优估计值：

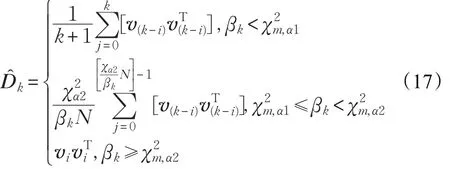
步骤3.4将 D̂k代入式（9）求取优化后的渐消因子 λ̂k。

步骤4将λ̂k代入式（8）计算加入渐消因子修正后的系统误差协方差。

步骤5通过式（5）～（7）计算卡尔曼增益、状态最优估计以及系统误差协方差，进行滤波更新。

步骤6如果算法未结束，k=k+1，进行步骤2。否则进行步骤7。

步骤7结束。

由算法工作流程和图1可知，基于IGGIII方案的自适应渐消卡尔曼滤波器滤波算法在进行滑动采样区间自适应求取时将新息马氏距离服从卡方分布作为判断准则进行新息异常判断，并引入IGGIII信息分类方案的思想，把新息分为可靠信息、可疑信息和有害信息三类，分析了造成新息出现波动和异常的原因，分别采取不同的滑动采样区间长度自适应策略。通过滑动采样区间长度的实时在线计算，实现系统不同噪声环境下渐消因子的求取，解决模型稳定情况下滑动采样区间过短造成的滤波精度降低和系统模型发生变化时滑动采样区间过长造成的动态跟踪性能无法满足需求的问题，避免滑动采样区间固定的弊端，实现滤波精度和动态性之间的平衡。

图1 基于IGGIII方案的自适应卡尔曼滤波器原理框图

4 实验仿真与结果分析

为验证改进算法的有效性，本文利用Matlab对二维平面内的小车行驶位置估计进行仿真实验。系统的状态方程和量测方程分别为：

式中，状态转移矩阵为：

观测矩阵为：

取位置以及速度作为系统状态变量，初始位置为（100，100），且 x轴初始运动速度2 m/s，y轴初始运动速度0 m/s，那么状态变量初始值x0=[ ]100 2 100 0。扫描周期为T=1 s，仿真时间100 s。滑动采样区间长度N在前20 s取k，20 s以后取20。目标小车在前50 s处于平稳行驶运动状态，在50 s至52 s进行机动。

本文利用以上仿真模型进行了卡尔曼滤波器（KF）、自适应渐消卡尔曼滤波器（AFKF）以及基于IGGIII方案的自适应渐消卡尔曼滤波器（IGGAFKF）的对比验证，仿真结果如图2所示。

图2 位置估计结果

如图2三种算法的位置估计仿真结果所示，IGGAFKF的滤波估计结果更加接近于目标的真实位置。KF和AFKF位置估计都存在不同程度的偏离。KF在目标机动位置出现较大估计偏差，AFKF滤波估计结果偏离程度要小于KF，但高于IGGAFKF。

图3分别展示了三种算法的位置误差对比。通过对比三种算法的误差曲线可知，在目标稳定行进过程中，AFKF的估计误差存在较大波动，IGGAFKF通过增大滑动采样区间长度，增强滤波鲁棒性，估计结果更加平稳、精确。在目标进行机动时，KF、AFKF、IGGAFKF误差都开始变大，但是IGGAFKF误差峰值明显低于KF及AFKF，说明IGGAFKF在目标运动状态发生较大变化时对于准确量测信息具有更好的动态跟踪性能，能够抑制模型不准造成的滤波发散。并且IGGAFKF通过减小滑动采样区间长度，在经过2次迭代后将误差控制在1 m范围内，KF和AFKF分别需要8次和4次，所以，IGGAFKF能够在滤波出现发散时实现快速收敛，提高滤波精度。由上可知，IGGAFKF在系统稳定情况下滤波结果更加精确，系统模型参数发生变化时具有更好的动态性，能够实现滤波精度与动态性之间的平衡，验证了此算法的可行性与优越性。

图3 位置估计误差对比

图4 显示了位置误差的占比。IGGAFKF 42%的采样点位置误差小于0.25 m，89%采样点位置误差小于0.5 m，100%的采样点误差小于2 m。KF相同误差的占比分别为38%、77%和89%。AFKF相同误差的占比为33%、77%和98%。且由表1中三种滤波算法的误差统计数据可知，IGGAFKF最大误差为1.66 m，明显小于KF和AFKF最大误差。IGGAFKF平均误差为0.32 m，相对于KF与AFKF的平均误差分别提升了121%、37%。因此，IGGAFKA具有更高的滤波估计精度。

图4 位置误差占比

表1 三种滤波算法误差统计 m

对100组位置仿真数据在CPU型号为Intel®CoreTMi5-4210U的计算机上进行10次测试，取耗费时间平均值，得到三种对比算法跑完100组数据耗费时间对比表。

由表2中数据可以发现，KF耗时最短，AFKF以及IGGAFKF相较于KF运算耗时都有所增加，但增加幅度较小。将IGGAFKF和AFKF耗时除以100，获得单组数据平均耗时分别为0.513 3 ms和0.468 1 ms，两者差值仅为0.045 2 ms，滤波效率下降8%。因此，IGGAFKF相较于AFKF滤波效率下降并不明显，能够保证滤波器的实时性要求。

表2 100组数据耗费时间

5 结束语

针对滑动采样区间长度单一带来的滤波精度与动态性之间的矛盾问题，本文提出了一种基于IGGIII方案的渐消自适应卡尔曼滤波器。该滤波器算法以新息马氏距离服从卡方分布作为新息异常判断标准，并引入IGGIII方案的信息分类思想，对不同噪声情况下的滑动采样区间长度N进行自适应优化选取。在保证滤波效率的同时，能够实现滤波精度与动态性之间的平衡。在船舶、飞行器、潜航器等设备的定位、制导与控制方面具有一定应用价值。