带有约束条件的零一膨胀Poisson回归模型
2020-07-17华志强
刘 影, 华志强
(1. 吉林师范大学 数学学院, 吉林 四平 136000; 2. 内蒙古民族大学 数学学院, 内蒙古 通辽 028043)
计数数据是实际生活中常见的一类数据类型, 可描述一个事件发生的次数, 通常用取值为自然数的随机变量表示. 该类数据在临床医学、 心理学、 遗传学、 环境学和金融学等领域应用广泛, Poisson模型、 二项模型和负二项模型是处理计数数据的传统方法, Poisson回归模型、 二项回归模型和负二项回归模型常用来刻画响应变量与解释变量之间的关系. 目前, 人们已对上述经典模型进行了多方面推广. 在实际应用中, 通常会遇到0过多的样本数据, 即0观测的比例远超过了拟合分布的允许范围, 此时, 传统的Poisson模型、 二项模型和负二项模型不再适用. 针对这种情形, 文献[1]首次提出了零膨胀数据; 文献[2-3]研究了不考虑协变量的零膨胀Poisson分布; 文献[4]建立了零膨胀Poisson回归模型; 文献[5]给出了零膨胀模型的Bayes方法; 文献[6]讨论了零膨胀数据的Bayes分位回归模型; 文献[7]给出了零膨胀分布参数的固定宽度置信区间的构造方法. 目前, 关于零膨胀计数数据的研究已有很多结果, 但在一些实际问题中, 样本不仅会出现0过多的情况, 也会出现1过多的情况, 例如: 在一段时间内, 某地交通事故发生的次数、 极端天气出现的次数、 某传染病的发病次数、 汽车保险的索赔次数等, 通常0和1出现的次数都比较多. 针对这种情形, 文献[8]提出了零一膨胀Poisson分布; 文献[9]研究了该分布的性质; 文献[10]给出了该分布参数的极大似然估计和Bayes估计; 文献[11]研究了零一膨胀Poisson回归模型及其统计推断方法; 文献[12]讨论了零一膨胀Poisson回归模型的非参数统计分析问题. 此外, 利用统计模型分析实际问题时还发现, 除需要知道样本信息外, 总体分布也会受某些条件的限制, 例如: 在考虑产品的合格率时, 由经验可知合格率的下限; 由于市场原因或者监管法规的影响, 产品的价格不能超过某值或者低于某值等. 因此, 模型参数空间受约束的统计模型已得到广泛关注[13-14]. 本文将该思想引入到零一膨胀模型中, 提出一类带有一般线性约束条件的零一膨胀Poisson回归模型, 并讨论相应的参数估计问题.
1 模型简介
令Z=(Z0,Z1,Z2)T服从多项分布,X服从Poisson分布, 即Z~Multinomial(1;φ0,φ1,φ2),X~Poisson(λ), 且Z与X相互独立. 如果
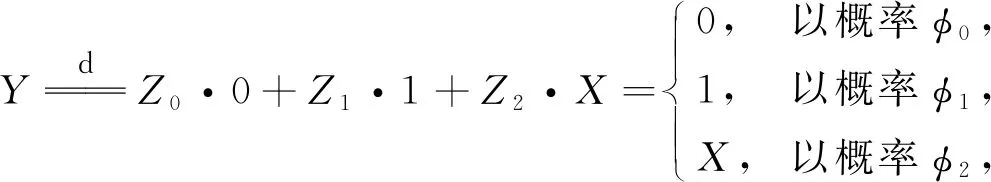
(1)

其中:P(ξ0=0)=1,P(ξ1=1)=1;φ0∈[0,1)和φ1∈[0,1)分别表示0和1的膨胀率,φ2=1-φ0-φ1∈(0,1]. 显然, 零一膨胀Poisson分布是3个随机变量的混合: 退化为0的随机变量、 退化为1的随机变量和Poisson随机变量. 特别地, 当φ0=0时, 零一膨胀Poisson分布即为一膨胀Poisson分布(OIP); 当φ1=0时, 零一膨胀Poisson分布即为零膨胀Poisson分布(ZIP); 当φ0=φ1=0时, 零一膨胀Poisson分布即为普通的Poisson分布.
由定义易知, 零一膨胀Poisson分布的分布函数为

E(Y)=φ1+φ2λ, Var(Y)=φ1(1-φ1)+φ2λ(1-2φ1)+φ2λ2(1-φ2).
零一膨胀Poisson分布的其他等价形式和性质参见文献[9].
在实际应用中, 模型参数通常会受一些外在因素的影响, 例如: 某人某段时期内到医院就诊的次数可能与其年龄和性别有关, 也可能与其居住地环境有关, 因此本文将协变量引入到零一膨胀Poisson分布的参数中, 得到零一膨胀Poisson回归模型. 本文只对参数λ进行回归分析, 即假设logλ=WTβ, 其中:W=(1,W1,W2,…,Wp)T为协变量;β=(β0,β1,…,βp)T为回归系数.
进一步, 统计模型经常有约束条件, 例如: 在医疗保险产品定价中, 某些风险类别的费率不能过高, 此时可假设回归系数满足如下线性约束:

(2)

2 参数估计
本文使用极大似然法进行参数估计, 并借助EM(expectation maximization)算法和Newton-Raphson算法求解, 下面给出迭代过程. 令θ=(φ0,φ1,βT)T为待估参数, 设Y1,Y2…,Yn为一组来自ZOIP(φ0,φ1,λi)的简单随机样本, 即各样本相互独立, 且
其中:i=1,2,…,n;

(3)
为使用EM算法, 引入潜变量Z0i和Z1i(i=1,2,…,n),Z0i=1表示观测值yi来自结构零(即式(1)的第一部分),Z0i=0表示观测值yi来自分布零(即式(1)的第三部分),Z1i=1表示观测值yi来自结构一(即式(1)的第二部分),Z1i=0表示观测值yi来自结构一(即式(1)的第三部分). 记y=(y1,…,yn),Z0=(Z01,…,Z0n),Z1=(Z11,…,Z1n), 则完整数据下的似然函数为
易得对数似然函数为
因此, 约束条件下零一膨胀Poisson回归模型的极大似然估计可表示为

考虑优化如下函数:

(4)
这里,η是一个较大的正数. 当不满足约束条件Aβ-c≤0时, 式(4)等号右边将减去一个较大的正数, 相当于对目标函数进行了“惩罚”, 从而对参数的估计值进行了重新优化.



其中:
这里

M-步(β): 令Q1(β)关于β的一阶导数为0, 即

(5)
其中:S=diag(s1,s2,…,sr),si=max{0,αi0β0+αi1β1+…+αipβp-ci};e=(1,1,…,1)T. 由于方程(5)没有显示解, 因此本文采用Newton-Raphson算法得到如下近似解:
其中:
M-步(φ0和φ1): 令Q2(φ0,φ1)分别关于φ0和φ1的一阶导数为0, 即

(6)

3 数值模拟与应用
假设φ0=0.5,φ1=0.3, 且lnλi=β1Wi1+β2Wi2(i=1,2,…,n), 其中β1=0.5,β2=-0.3, {Wi1,i≥1}和{Wi2,i≥1}均为独立同分布随机变量序列, 其共同分布都是Bernoulli分布B(1,0.5). 用R语言产生1 000个零一膨胀Poisson回归模型的随机数, 图1为其频率直方图. 模拟500次取估计值的平均数, 无约束条件下各参数的估计结果为:φ0=0.484 8,φ1=0.291 0,β1=0.605 4,β2=-0.234 9.
假设根据实际情形, 需对W1=1,W2=0类别的个体进行限制, 例如: 取A=(1,0),c=0.55, 考虑约束条件Aβ≤c, 即β1≤0.55, 则可得修正后的参数估计结果为:φ0=0.479 4,φ1=0.285 4,β1=0.459 1,β2=-0.197 4.
综上可见, 本文方法使得参数的估计结果满足约束条件, 具有一定的可行性和有效性.
选择一组澳大利亚新南威尔士州水资源委员会冲浪/健康研究机构提供的耳病发生次数数据(http://www.statsci.org/data/oz/earinf.html), 该数据集给出了1990年287组个体观测数据. 响应变量是每个观测者的耳病发生次数, 其中发生次数为0的人数占总人数的52.6%, 发生次数为1的人数占总人数的13.9%. 解释变量包括游泳频率、 游泳地点、 观测者的年龄和性别. 此时, 式(3)的回归模型可写为
logλi=β0+β1Wi1+β2Wi2+β3Wi3+β4Wi4,
其中:Wi1表示游泳频率,Wi1=1表示观测者经常游泳,Wi1=0表示观测者不经常游泳;Wi2表示游泳地点,Wi2=1表示观测者在海滨游泳,Wi2=0表示观测者不在海滨游泳;Wi3表示年龄,Wi3=1表示观测者年龄为15~24岁,Wi3=0表示观测者年龄为25~29岁;Wi4表示性别,Wi4=1表示观测者为女性,Wi4=0表示观测者为男性.
耳病发生次数的分布如图2所示. 由图2粗略可见, 超过1/2观测者的耳病发生次数为0, 也有较多观测者的耳病发生次数为1, 表明该数据集存在零一膨胀特点, 适用于零一膨胀模型. 无约束条件下各参数的估计结果为:φ0=0.505 2,φ1=0.121 4,β0=1.519 3,β1=-0.541 8,β2=-0.076 3,β3=-0.147 7,β4=-0.049 0.
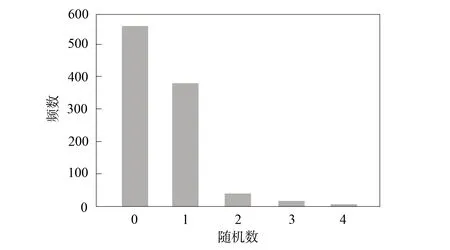
图1 随机数的频数直方图

图2 耳病发生次数的分布
为说明约束条件的影响, 考虑因为λ=E(Y|Z3=1), 因而λ可理解为观测者发生耳病的高风险部分, 在审核相应的保险产品费率时, 其具有重要作用. 假设在市场条件下, 行业政策规定针对这部分的费率不能过高, 如不允许超过4. 下面考虑在该约束条件下的模型和参数估计. 记
此时, 可在模型中加入约束条件Aβ≤c, 并得到约束条件下各参数的估计结果:φ0=0.505 5,φ1=0.120 8,β0=1.386 5,β1=-0.455 4,β2=-0.015 1,β3=-0.085 3,β4=-0.000 2.
按照解释变量W1,W2,W3,W4的不同取值, 观测者可被分为16组, 其中第i组解释变量的取值对应矩阵A第i行中第2列~第5列元素, 例如: 第一组对应W1=0,W2=0,W3=0,W4=0, 第二组对应W1=0,W2=1,W3=0,W4=0, 以此类推. 表1列出了不同组在约束前后的λ预测值. 由表1可见, 约束前有4组λ的预测值超过4, 而约束条件改变了参数的估计结果, 使得所有组的λ预测值都不超过4, 且所有组的λ预测值总和变化不大, 表明相关医疗保险产品的定价受市场原因或者政策法规的影响较小, 但模型在约束前后得到的总价格保持不变, 兼顾了保险公司的利益, 因而本文的模型和方法能满足预期目标, 有一定的实用价值.

表1 有约束条件和无约束条件下λ的预测值比较
