K3,5,p的点可区别的一般全染色

杨佳睿, 陈祥恩

(西北师范大学 数学与统计学院, 兰州 730070)

0 引 言

目前, 关于图的点可区别一般边染色研究已有很多结果[1-7]. 文献[8]提出了图的一般点可区别全染色的概念. 图G的一般全染色是指若干种颜色对图G的全部顶点及边的一个分配. 设f是图G的一般全染色,x为G的一个顶点, 将在f下x的颜色及与x关联的边的颜色所构成的集合记为Cf(x)或C(x), 称为顶点x在f下的色集合. 设f是图G的一般全染色. 若对图G的任意两个不同的顶点u,v, 有C(u)≠C(v), 则f称为图G的点可区别一般全染色(简记为GVDTC). 对图G进行点可区别一般全染色所需的最少颜色数称为G的点可区别一般全色数, 记为χgvt(G). 图G的k-一般全染色是指使用了k种颜色的图G的一般全染色. 图G的点可区别一般全染色也称为图G的一般点可区别全染色(简记为GVDTC)[8]. 图G的k-一般点可区别全染色是指图G使用了k种颜色的一般点可区别全染色(简记为k-GVDTC). 点可区别一般全色数也称为一般点可区别全色数. 文献[8]研究了路、 圈、 星、 双星、 三星、 轮、 扇和完全图的一般点可区别全染色； 文献[9-11]研究了另外几类完全三部图的点可区别一般全染色.

本文研究K3,5,p的点可区别一般全染色, 并给出其一般点可区别全色数. 本文讨论的完全三部图Km,n,p的顶点集合为V=X∪Y∪Z, 边集合为{xiyj|i=1,2,…,m;j=1,2,…,n}∪{yjzt|j=1,2,…,n;t=1,2,…,p}∪{xizt|i=1,2,…,m;t=1,2,…,p}, 其中:X={x1,x2,…,xm};Y={y1,y2,…,yn};Z={z1,z2,…,zp}. 本文约定给出一个图的l-GVDTC时, 所使用的l种颜色为1,2,…,l.

1 预备知识

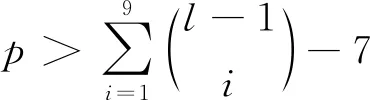
证明： 先用反证法证明K3,5,p不存在(l-1)-GVDTC, 再具体构造出K3,5,p的l-GVDTC. 假设K3,5,p存在(l-1)-GVDTC.

断言1) 任意1-子集都不是X∪Y中任一点的色集合.

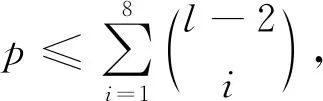
断言2) 至少3个1-子集不是Z中任一点的色集合.

否则, 不妨设仅有{1},{2}这两个集合不是Z中任一点的色集合, 则{3},{4},…,{l-1}均是Z中点的色集合, 即C(xi)∩C(yj)⊇{3,4,…,l-1}, 从而X,Y中每个点可分配的色集合有{3,4,…,l-1},{1,3,4,…,l-1},{2,3,4,…,l-1},{1,2,3,…,l-1}, 而这4个集合不能区分X,Y中的8个顶点, 矛盾.

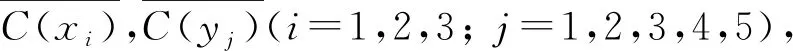
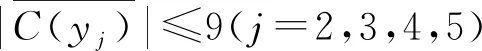
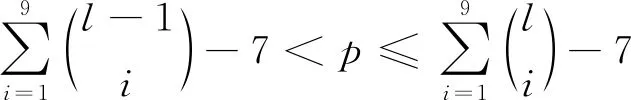
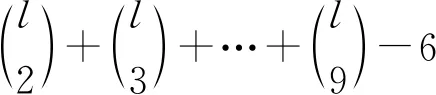
下面给出K3,5,p的一个l-GVDTCf. 令f(xi)=1(i=1,2,3),f(yj)=2(j=1,2,3,4,5). 用maxD(zi)染点zi(i=1,2,…,p). 而zi的关联边均染以i+6(i=1,2,…,l-6).

当|D(zi)|=2时,f(uzi)=min{D(u)∩D(zi)},u∈X∪Y. 当|D(zi)|=3时,f(uzi)=min{D(u)∩D(zi)},u∈{x2,x3,y1,y2,y3,y4,y5},f(x1zi)=min{D(x1)∩D(zi){f(x2zi),f(x3zi),f(yjzi)}},j=1,2,3,4,5. 当|D(zi)|=4时,f(uzi)=min{D(u)∩D(zi)},u∈{x3,y1,y2,y3,y4,y5},f(x2zi)=min{D(x2)∩D(zi){f(x3zi),f(yjzi)}},j=1,2,3,4,5;f(x1zi)=min{D(x1)∩D(zi){f(x2zi),f(x3zi),f(yjzi)}},j=1,2,3,4,5. 当|D(zi)|=5时,f(uzi)=min{D(u)∩D(zi)},u∈{y1,y2,y3,y4,y5},f(x3zi)=min{D(x3)∩D(zi){f(yjzi)}},j=1,2,3,4,5;f(x2zi)=min{D(x2)∩D(zi){f(x3zi),f(yjzi)}},j=1,2,3,4,5;f(x1zi)=min{D(x1)∩D(zi){f(x2zi),f(x3zi),f(yjzi)}},j=1,2,3,4,5. 当|D(zi)|=6时,f(uzi)=min{D(u)∩D(zi)},u∈{y2,y3,y4,y5},f(y1zi)=min{D(y1)∩D(zi){f(yjzi)}},j=2,3,4,5;f(x3zi)=min{D(x3)∩D(zi){f(yjzi)}},j=1,2,3,4,5;f(x2zi)=min{D(x2)∩D(zi){f(x3zi),f(yjzi)}},j=1,2,3,4,5;f(x1zi)=min{D(x1)∩D(zi){f(x2zi),f(x3zi),f(yjzi)}},j=1,2,3,4,5. 当|D(zi)|=7时,f(uzi)=min{D(u)∩D(zi)},u∈{y3,y4,y5},f(y2zi)=min{D(y2)∩D(zi){f(yjzi)}},j=3,4,5;f(y1zi)=min{D(y1)∩D(zi){f(yjzi)}},j=2,3,4,5;f(x3zi)=min{D(x3)∩D(zi){f(yjzi)}},j=1,2,3,4,5;f(x2zi)=min{D(x2)∩D(zi){f(x3zi),f(yjzi)}},j=1,2,3,4,5;f(x1zi)=min{D(x1)∩D(zi){f(x2zi),f(x3zi),f(yjzi)}},j=1,2,3,4,5. 当|D(zi)|=8时,f(uzi)= min{D(u)∩D(zi)},u∈{y4,y5},f(y3zi)=min{D(y3)∩D(zi){f(yjzi)}},j=4,5;f(y2zi)=min{D(y2)∩D(zi){f(yjzi)}},j=3,4,5;f(y1zi)=min{D(y1)∩D(zi){f(yjzi)}},j=2,3,4,5;f(x3zi)=min{D(x3)∩D(zi){f(yjzi)}},j=1,2,3,4,5;f(x2zi)=min{D(x2)∩D(zi){f(x3zi),f(yjzi)}},j=1,2,3,4,5;f(x1zi)=min{D(x1)∩D(zi){f(x2zi),f(x3zi),f(yjzi)}},j=1,2,3,4,5. 当|D(zi)|=9时,f(y5zi)=min{D(u)∩D(zi)},f(y4zi)=min{D(y4)∩D(zi){f(y5zi)}},f(y3zi)=min{D(y3)∩D(zi){f(yjzi)}},j=4,5;f(y2zi)=min{D(y2)∩D(zi){f(yjzi)}},j=3,4,5;f(y1zi)=min{D(y1)∩D(zi){f(yjzi)}},j=2,3,4,5;f(x3zi)=min{D(x3)∩D(zi){f(yjzi)}},j=1,2,3,4,5;f(x2zi)=min{D(x2)∩D(zi){f(x3zi),f(yjzi)}},j=1,2,3,4,5;f(x1zi)=min{D(x1)∩D(zi){f(x2zi),f(x3zi),f(yjzi)}},j=1,2,3,4,5.

对∀x∈X,y∈Y, 用min{D(x)∩D(y)}染边xy, 最后得到K3,5,p的l-IE全染色f, 是点可区别的, 因为∀v∈V(K3,5,p), 均有C(v)=D(v).

2 主要结果

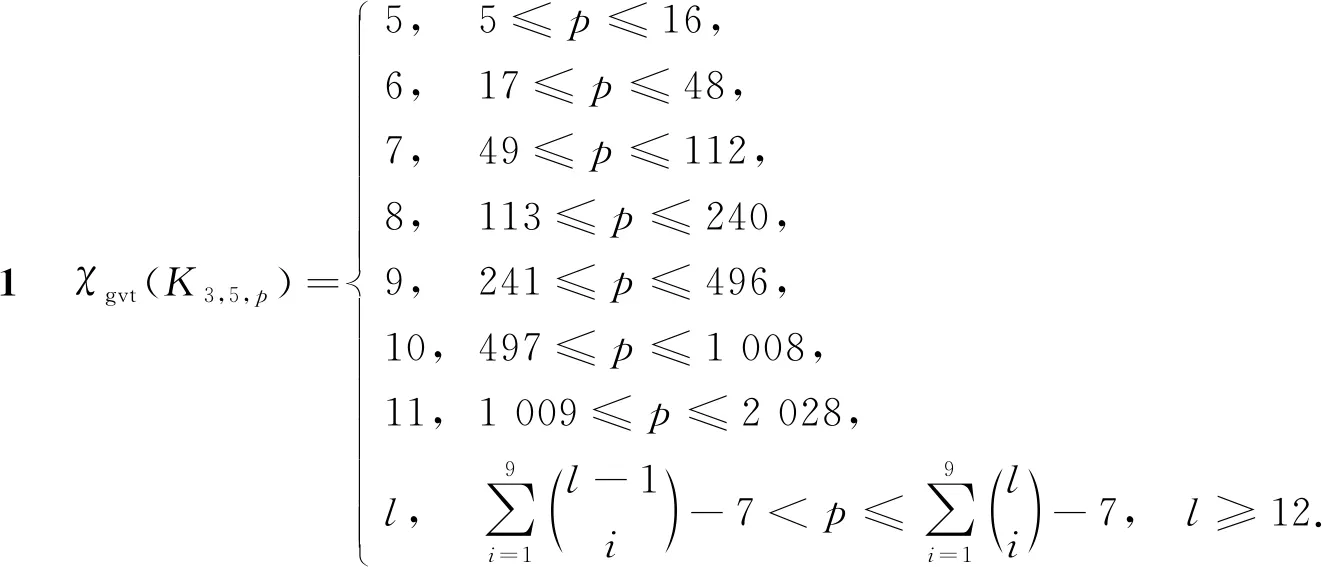
证明： 分以下8种情形进行讨论.

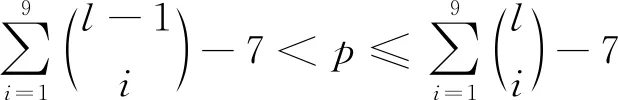
情形2) 当1 009≤p≤2 028时,χgvt(K3,5,p)=11.

先用反证法证明K3,5,p不存在10-GVDTC, 再构造出K3,5,p的11-GVDTC. 假设K3,5,p存在10-GVDTC.

断言① 任意1-子集均不是X∪Y中任一点的色集合.

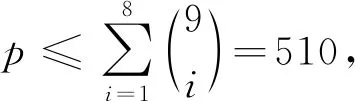
断言② 至少3个1-子集不是Z中任一点的色集合.

否则, 不妨设仅有{1},{2}这两个集合不是Z中任一点的色集合, 则{3},{4},…,{9}均是Z中点的色集合, 即有C(xi)∩C(yj)⊇{3,4,…,10}, 从而X,Y中每个点可分配的色集合有{3,4,…,10},{1,3,4,…,10},{2,3,4,…,10},{1,2,3,…,10}, 4个集合不能区分X,Y中的8个顶点, 矛盾.

下面给出K3,5,2 028的11-GVDTC, 令D(x1)={1,2,…,11},D(x2)=D(x1){1},D(x3)=D(x1){2},D(y1)=D(x1){3},D(y2)=D(x1){4},D(y3)=D(x1){5},D(y4)=D(x1){6},D(y5)=D(x1){7}. 将除{1},{2},{3},{4},{5},{6},{7}外的{1,2,…,11}的其余1-子集,2-子集,…,9-子集作为Z中点的色集合, 参照引理2证明过程所述的染色法可给出K3,5,2 028的11-GVDTC.

情形3) 当497≤p≤1 008时,χgvt(K3,5,p)=10.

证明： 先用反证法证明K3,5,p不存在9-GVDTC, 再构造出K3,5,p的10-GVDTC. 假设K3,5,p存在9-GVDTC.

断言① 任意1-子集不是X∪Y中任一点的色集合.

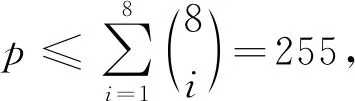
断言② 至少3个1-子集不是Z中任一点的色集合.

否则, 不妨设仅有{1},{2}这两个集合不是Z中任一点的色集合, 则{3},{4},…,{9}均是Z中点的色集合, 即有C(xi)∩C(yj)⊇{3,4,…,9}, 从而X,Y中每个点可分配的色集合有{3,4,…,9},{1,3,4,…,9},{2,3,4,…,9},{1,2,3,…,9}, 4个集合不能区分X,Y中的8个顶点, 矛盾.

下面给出K3,5,1 028的10-GVDTC, 令D(x1)={1,2,…,10},D(x2)=D(x1){1},D(x3)=D(x1){2},D(y1) =D(x1){3},D(y2)=D(x1){4},D(y3)=D(x1){5},D(y4)=D(x1){6},D(y5)=D(x1){7}. 将除{1},{2},{3},{4},{5},{6},{7}外的{1,2,…,10}的其余1-子集,2-子集,…,9-子集作为Z中点的色集合, 参照引理2证明过程所述的染色法可给出K3,5,1 008的10-GVDTC.

情形4) 当241≤p≤496时,χgvt(K3,5,p)=9.

证明： 先用反证法证明K3,5,p不存在8-GVDTC, 再构造出K3,5,p的9-GVDTC. 假设K3,5,p存在8-GVDTC.

断言① 任意1-子集不是X∪Y中任一点的色集合.

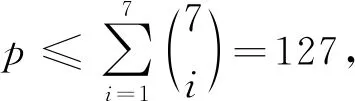
断言② 至少3个1-子集不是Z中任一点的色集合.

否则, 不妨设仅有{1},{2}这两个集合不是Z中任一点的色集合, 则{3},{4},…,{8}均是Z中点的色集合, 即有C(xi)∩C(yj)⊇{3,4,…,8}, 从而X,Y中每个点可分配的色集合有{3,4,…,8},{1,3,4,…,8},{2,3,4,…,8},{1,2,3,…,8}, 4个集合不能区分X,Y中的8个顶点, 矛盾.

下面给出K3,5,496的9-GVDTC, 令D(x1)={1,2,…,9},D(x2)=D(x1){1},D(x3)=D(x1){2},D(y1)=D(x1){3},D(y2)=D(x1){4},D(y3)=D(x1){5},D(y4)=D(x1){6},D(y5)=D(x1){7}. 将除{1},{2},{3},{4},{5},{6},{7}外的{1,2,…,9}的其余1-子集,2-子集,…,8-子集作为Z中点的色集合, 参照引理2证明过程所述的染色法可给出K3,5,496的9-GVDTC.

情形5) 当113≤p≤240时,χgvt(K3,5,p)=8.

证明： 先用反证法证明K3,5,p不存在7-GVDTC, 再构造出K3,5,p的8-GVDTC. 假设K3,5,p存在7-GVDTC.

断言① 任意1-子集不是X∪Y中任一点的色集合.

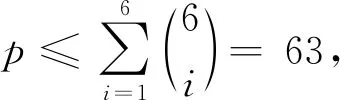
断言② 至少3个1-子集不是Z中任一点的色集合.

否则, 不妨设仅有{1},{2}这两个集合不是Z中任一点的色集合, 则{3},{4},…,{7}均是Z中点的色集合, 即有C(xi)∩C(yj)⊇{3,4,…,7}, 从而X,Y中每个点可分配的色集合有{3,4,…,7},{1,3,4,…,7},{2,3,4,…,7},{1,2,3,…,7}, 4个集合不能区分X,Y中的8个顶点, 矛盾.

下面给出K3,5,240的8-GVDTC, 令D(x1)={1,2,…,8},D(x2)=D(x1){1},D(x3)=D(x1){2},D(y1)=D(x1){3},D(y2)=D(x1){4},D(y3)=D(x1){5},D(y4)=D(x1){6},D(y5)=D(x1){7}. 将除{1},{2},{3},{4},{5},{6},{7}外的{1,2,…,8}的其余1-子集,2-子集,…,7-子集作为Z中点的色集合, 参照引理2证明过程所述的染色法可给出K3,5,240的8-GVDTC.

情形6) 当49≤p≤112时,χgvt(K3,5,p)=7.

证明： 先用反证法证明K3,5,p不存在6-GVDTC, 再构造出K3,5,p的7-GVDTC. 假设K3,5,p存在6-GVDTC.

断言① 任意1-子集不是X∪Y中任一点的色集合.

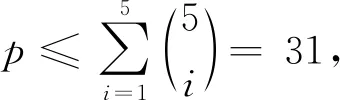
断言② 任意2-子集均不是X∪Y中任一点的色集合.

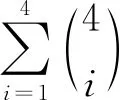
断言③ 至少3个1-子集不是Z中任一点的色集合.

否则, 不妨设仅有{1},{2}这两个集合不是Z中任一点的色集合, 则{3},{4},{5},{6}均是Z中点的色集合, 即有C(xi)∩C(yj)⊇{3,4,5,6}, 从而X,Y中每个点可分配的色集合有{3,4,5,6},{1,3,4,5,6},{2,3,4,5,6},{1,2,3,4,5,6}, 4个集合不能区分X,Y中的8个顶点, 矛盾.

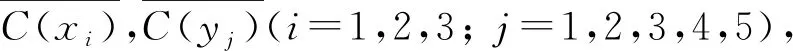
下面给出K3,5,112的7-GVDTC, 令D(x1)={1,2,…,7},D(x2)=D(x1){1},D(x3)=D(x1){2},D(y1)=D(x1){3},D(y2)=D(x1){4},D(y3)=D(x1){5},D(y4)=D(x1){6},D(y5)=D(x1){7}. 将除{1},{2},{3},{4},{5},{6},{7}外的{1,2,…,7}的其余2-子集,3-子集,…,7-子集作为Z中点的色集合, 参照引理2证明过程所述的染色法可给出K3,5,112的7-GVDTC.

情形7) 当17≤p≤48时,χgvt(K3,5,p)=6.

证明： 先用反证法证明K3,5,p不存在5-GVDTC, 再构造出K3,5,p的6-GVDTC. 假设K3,5,p存在5-GVDTC.

断言① 任意1-子集不是X∪Y中任一点的色集合.

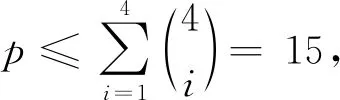
断言②X∪Y中至多存在1个2-子集.

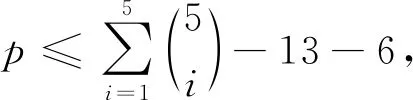
断言③ 至少3个1-子集不是Z中任一点的色集合.

否则, 不妨设仅有{1},{2}这两个集合不是Z中任一点的色集合, 则{3},{4},{5}均是Z中点的色集合, 即有C(xi)∩C(yj)⊇{3,4,5}, 从而X,Y中每个点可分配的色集合有{3,4,5},{1,3,4,5},{2,3,4,5}，{1,2,3,4,5}, 4个集合不能区分X∪Y中的8个顶点, 矛盾.

下面给出K3,5,48的6-GVDTC, 令D(x1)={1,2,…,6},D(x2)=D(x1){1},D(x3)=D(x1){2},D(y1)=D(x1){3},D(y2)=D(x1){4},D(y3)=D(x1){1,2},D(y4)=D(x1){1,3},D(y5)=D(x1){1,4}. 将除{1},{2},{3},{4},{1,2},{1,3},{1,4}外的{1,2,…,6}的其余1-子集,2-子集,…,6-子集作为Z中点的色集合, 参照引理2证明过程所述的染色法可给出K3,5,48的6-GVDTC.

情形8) 当5≤p≤16时,χgvt(K3,5,p)=5.

证明： 先用反证法证明K3,5,p不存在4-GVDTC, 再构造出K3,5,p的5-GVDTC. 假设K3,5,p存在4-GVDTC.

断言① 任意1-子集不是X中任一点的色集合.

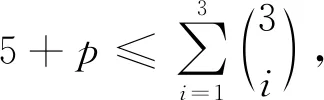
断言② 任意1-子集不是Y中任一点的色集合.

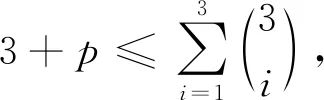
断言③ 至少3个1-子集不是Z中任一点的色集合.

否则, 不妨设{1},{2}不是Z中任一点的色集合, 则{3},{4}是Z中点的色集合, 即有C(xi)∩C(yj)⊇{3,4}, 从而X,Y中每个点可分配的色集合有{3,4},{1,3,4},{2,3,4},{1,2,3,4}, 4个集合不能区分X,Y中的8个顶点, 矛盾.

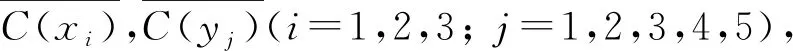
下面给出K3,5,16的5-GVDTC, 令D(x1)={1,2,…,5},D(x2)=D(x1){1},D(x3)=D(x1){2},D(y1)=D(x1){3},D(y2)=D(x1){4},D(y3)=D(x1){1,2},D(y4)=D(x1){1,3},D(y5)=D(x1){1,4}. 将除{1},{2},{3},{4},{1,2},{1,3},{1,4}外的{1,2,…,5}的其余1-子集,2-子集,…,5-子集作为Z中点的色集合, 参照引理2证明过程所述的染色法可给出K3,5,16的5-GVDTC.