算子代数上强保持k-斜Jordan乘积的映射

2020-07-17齐霄霏

吉林大学学报（理学版） 2020年4期

贾娟, 齐霄霏

(1. 太原学院应用数学系, 太原 030012; 2. 山西大学数学科学学院, 太原 030006)

0 引言

令R是具有对合运算*的环, 也称为*-环. 对任意的a,b∈R, 定义*{a,b}=ab+ba*, 称为a,b的斜Jordan乘积[1-2]. 假设f:R→R为一个映射. 若*{f(a),f(b)}=f(*{a,b})对所有元a,b∈R均成立, 则称f是保持斜Jordan乘积的; 若*{f(a),f(b)}=*{a,b}对所有元a,b∈R均成立, 则称其为强保持斜Jordan乘积的. Li等[3]证明了因子von Neumann代数上保持斜Jordan乘积的双射是*-环同构; Dai等[4]把上述结果推广到更一般的von Neumann代数上, 证明了任意两个von Neumann代数上(假设其中一个代数不含中心交换投影)保持斜Jordan乘积的双射是线性*-同构与共轭线性*-同构之和; 文献[5]讨论了C*-代数上保持斜Jordan乘积映射的可加性. 假设A与B是两个素C*-代数, 文献[5]证明了: 从A到B上的双射Φ若保单位元, 且满足Φ(*{A,P})=*{Φ(A),Φ(P)}对所有元A∈A及P∈{P1,IA-P1}成立, 其中P1是A中某个固定的非平凡投影, 则Φ必为*-可加的. 对于强保持斜Jordan乘积的映射, Taghavi等[6]证明了: 任意von Neumann代数A上的满射Φ, 若满足*{Φ(T),Φ(P)}=*{T,P}对所有T∈A和所有投影P∈A成立, 则Φ(I)是A中的中心元, 且存在从A中自伴元全体构成的集合到其中心的映射h, 使得对任意自伴元T,h(T)是中心自伴元, 且有Φ(T)=TΦ(I)+ih(T)成立.

更一般地, 对于任意正整数k≥1, 可给出k-斜Jordan乘积的定义. 定义a,b的k-斜Jordan乘积为*{a,b}k=*{a,*{a,b}k-1}, 其中:*{a,b}0=b;*{a,b}1=*{a,b}=ab+ba*. 显然, 当k=1时,a,b的k-斜Jordan乘积即为a,b的斜Jordan乘积. 对于映射f, 若*{f(a),f(b)}k=f(*{a,b}k)对所有元a,b∈R均成立, 则称f是保持k-斜Jordan乘积的; 若*{f(a),f(b)}k=*{a,b}k对所有元a,b∈R均成立, 则称其为强保持k-斜Jordan乘积的. 当k=3时, 文献[7-9]对算子代数上保持k-斜Jordan乘积映射进行了刻画. 但对于算子代数上强保持k-斜Jordan乘积映射的研究目前尚未见文献报道. 本文尝试给出一些重要算子代数上强保持k-斜Jordan乘积映射的具体刻画形式, 其中k为任意正整数. 注意到

其中

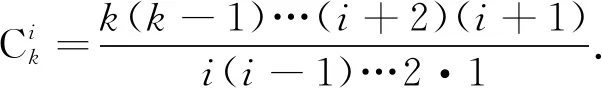
可见随着k的增加, 刻画强保持k-斜Jordan乘积映射的问题越来越困难. 本文在一般的*-素环上讨论强保持k-斜Jordan乘积映射的刻画问题. 令R是特征不为2、且含有非平凡对称幂等元e与单位元1的素*-环. 假设f:R→R是满射,k≥1是任意正整数. 本文证明f强保持k-斜Jordan乘积当且仅当存在满足条件λk+1=1的对称元λ∈C, 使得f(x)=λx对所有元x∈R均成立.

1 主要结果

设R表示一个环,Z(R)为其中心. 回忆R的特征(记为charR)是指满足条件dx=0对所有元x∈R均成立的最小正整数d. 如果不存在这样的d, 则称R的特征为0. 若对任意a,b∈R,aRb={0}蕴涵a=0或b=0, 则称R是素的.Q=Qml(R)表示极大左商环.Q的中心C=C(R)称为R的扩展中心. 如果R是素的, 则Q也是素的, 且C是一个域. 此外,Z(R)⊆C. 如果R还是一个*-环, 则R上的*运算可自然地延拓到C上, 此时称CS={λ∈C:λ=λ*}为R的对称扩展中心.

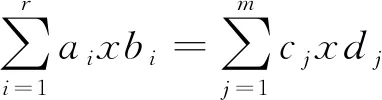
定理1令R是特征不为2、且含有非平凡对称幂等元e与单位元1的素*-环. 假设f:R→R是满射,k≥1是任意正整数. 则f强保持k-斜Jordan乘积, 即f满足*{f(x),f(y)}k=*{x,y}k对所有元x,y∈R均成立, 当且仅当存在满足条件λk+1=1的对称元λ∈CS, 使得f(x)=λx对所有元x∈R均成立.

证明: 设e∈R是非平凡对称幂等元, 并记e1=e,e2=1-e. 则R可分解为

R=R11+R12+R21+R22,

其中Rij=eiRej(i,j∈{1,2}).

首先, 通过直接计算可知下式成立:

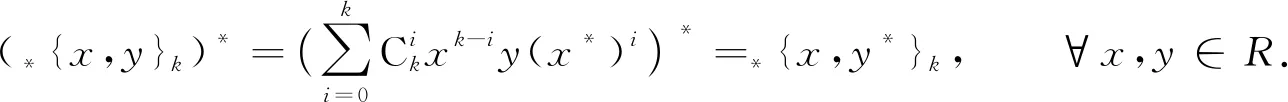
(1)

充分性显然. 对于必要性, 下面分8步证明. 利用f的满射性知, 存在元a∈R使得

f(a)=1.

(2)

1)f是可加的.

对任意元x,y∈R, 利用等式(2), 有

即得

2k(f(x+y)-f(x)-f(y))=0.

由于R的特征不为2, 即蕴涵f(x+y)=f(x)+f(y)对所有元x,y∈R均成立, 因此f是可加的.

2) 对任意元x∈R, 有f(x*)=f(x)*.

任取x∈R, 利用式(1),(2), 有

即蕴涵f(x)*=f(x*)对所有元x∈R均成立.

3) 对i∈{1,2}, 下列表述成立:

①f(ei)k+1=ei且f(ei)∈Rii;

② 对任取元xii∈Rii, 存在元rii∈Rii使得f(rii)=xii.

令f(e1)=s=s11+s12+s21+s22. 由结论2)知f(e1)=f(e1)*, 即

(3)

一方面, 注意到

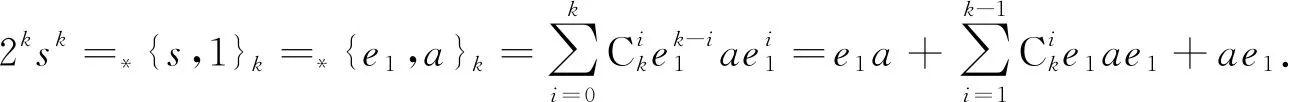
(4)

在式(4)左右两边分别乘以e2, 并利用R的特征不为2, 可得e2ske2=0. 另一方面, 由于*{f(e1),f(e1)}k=*{e1,e1}k, 所以2kf(e1)k+1=2ke1, 即有f(e1)k+1=e1, 从而

sk+1=e1ske1s+e1ske2s+e2ske1s=se1ske1+se1ske2+se2ske1=e1.

即

利用式(6)～(8),(11), 可得

类似地, 利用式(5),(9),(10),(12), 可得s21=0.

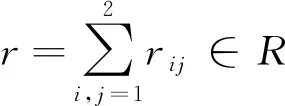
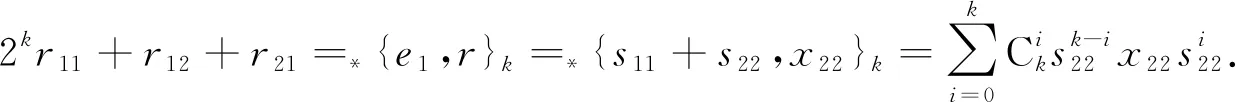
(13)

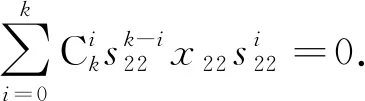
类似可证f(e2)k+1=e2,f(e2)∈R22, 且对任取元x11∈R11, 存在元r11∈R11使得f(r11)=x11.

4) 对任意元xij∈Rij, 有f(xij)=f(ei)xij=xijf(ej),i≠j∈{1,2}.

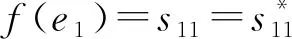
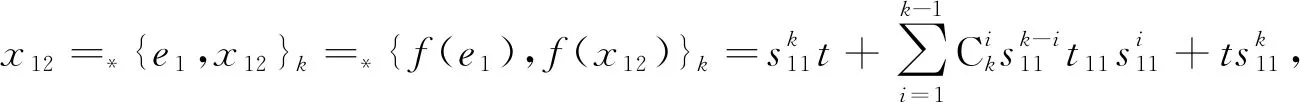
(14)

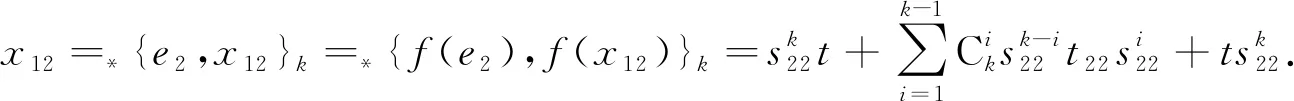
(15)

t12=s11x12=f(e1)x12,t21=0.

类似地, 利用式(15)可证t12=x12s22=x12f(e2).

下面证明t11=t22=0. 由f的满射性与结论3)中②知, 存在元r11∈R11使得f(r11)=e1, 则有

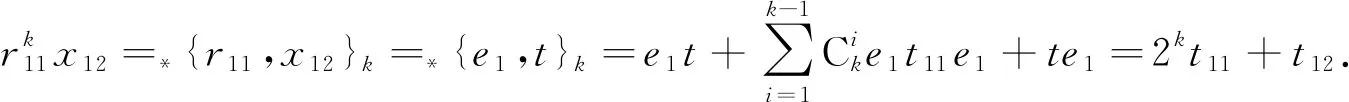
(16)

式(16)蕴涵t11=0. 类似可证t22=0.

5) 对任意元xii∈Rii, 有f(xii)∈Rii+Rjj,i≠j∈{1,2}.

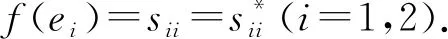
6) 存在满足条件λk+1=1的对称元λ∈CS, 使得f(ei)=λei, 且对任意元xii∈Rii, 有f(xii)=λxii,i=1,2.

这里只给出i=1情形的证明, 另一种情形类似可证. 任取xij∈Rij(i,j∈{1,2}). 注意到

再由1)和4)(为方便, 令f(e1)=s11), 有

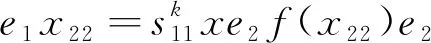
(20)

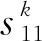
e2f(x22)e2=λx22

(21)

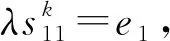
式(22)蕴涵e1f(x22)e1=0, 再结合式(21)与结论5), 即得f(x22)=λx22对所有x22∈R22成立.

7) 对任意元xij∈Rij, 有f(xij)=λxij,i≠j∈{1,2}.

由结论4)和6)可知, 对任意的x12∈R12与x21∈R21, 有

f(x12)=f(e1)x12=λx12,

f(x21)=x21f(e1)={λ}x21.

8) 对任意元x∈R, 有f(x)=λx.

任取x=x11+x12+x21+x22∈R. 利用结论1),6),7), 易验证结论成立. 证毕.

2 主要结果在算子代数上的应用

如果R是一个素C*-代数, 则利用文献[11]中推论2.4知, 其扩展中心为C(R)=(复数域). 因此CS(R)=(实数域). 由定理1知下列推论显然.

推论1令R是含单位元与一非平凡自伴幂等元的素C*-代数. 假设Φ:R→R是一个满射, 则Φ强保持k-斜Jordan乘积当且仅当下列结论之一成立:

1) 若k是奇数, 则Φ(A)=A对所有A∈R均成立, 或者Φ(A)=-A对所有A∈R均成立；

2) 若k是偶数, 则Φ(A)=A对所有A∈R均成立.

令B(H)表示复Hilbert空间H上有界线性算子全体组成的代数.回忆von Neumann代数M是B(H)的子代数, 且满足二次换位性质: M ″=M, 其中M ′={T:T∈B(H),TA=AT, ∀A∈M }, M ″={M ′}′. 特别地, 若M的中心是I, 则称M是因子von Neumann代数.

注意到von Neumann代数是含单位元的C*-代数, 且包含许多非平凡的自伴幂等元; 此外, 因子von Neumann代数是素的. 因此, 利用推论1, 可得:

推论2假设M是因子von Neumann代数,Φ: M→M是满射, 则Φ强保持k-斜Jordan乘积当且仅当下列结论之一成立:

1) 若k是奇数, 则Φ(A)=A对所有A∈M均成立, 或者Φ(A)=-A对所有A∈M均成立；

2) 若k是偶数, 则Φ(A)=A对所有A∈M均成立.