双机器人松协调装配轨迹规划方法研究

姚俊，李俊渊，李明富,b

(湘潭大学 a. 机械工程学院； b. 复杂轨迹加工工艺及装备教育部工程研究中心，湖南 湘潭 411105)

0 引言

双机器人装配可以改善单机器人装配工作空间有限、灵活度不够等缺陷。在常见的双机器人装配过程中，双机器人之间的位置姿态约束关系是动态变化的，所以双机器人协调装配过程为松协调。通常情况下，双机器人装配主要任务分为两个阶段：第一阶段为抓取阶段，即在有障碍的环境中主-从机器人各自抓取配件，绕过障碍物寻找一条避免碰撞干涉的路径到达指定的装配位置，为协调装配做准备[1-3]；第二阶段为松协调装配阶段，即主-从机器人在装配体之间的约束下进行相对装配运动[4-7]。

为了满足协调装配中双机器人的轨迹连续性和约束关系，本文采用B样条曲线对关节轨迹进行插值，并对插值引起的装配误差进行补偿，以保证装配体之间的约束和驱动器的平稳性。量子粒子群算法(QPSO)[8]具有寻优能力较好、能够快速收敛到全局最优点、所需调整的参数较少、算法易于实现等优点，可以规划出较平滑的关节轨迹，且优化效率较高。

1 双机器人协调装配运动学分析

1.1 双机器人协调系统坐标系

对双机器人协调系统中的机器人和装配体分别建立坐标系，坐标系简图与实物图分别如图1(a)、图1(b)所示。用i表示机器人代号，i=1,2；在双机器人协调装配系统中，夹持装配体A的1号机器人为主机器人，夹持装配体B的2号机器人为从机器人；{Ri}为主-从机器人的基坐标系；{Ei}为主-从机器人末端的坐标系；{WPi}为主-从机器人所夹装配体的坐标系；{Pi}为装配任务点的坐标系。

图1 双机器人协调装配系统坐标系简图和实物图

1.2 协调装配误差分析

为了适应机器人控制器对驱动器控制的非连续性和平滑性，需要对主机器人轨迹进行插值，而插值得到的轨迹不能保证主机器人严格地按照任务要求进行连续直线运动，进而产生装配误差。而细微的误差会导致装配体上产生巨大的力或者力矩，使装配体产生变形，甚至损坏机器人。因此分析装配误差和规划出满足位置约束、姿态约束关系的双机器人协调装配轨迹是很有必要的。

对于轴孔装配模型，轴孔装配中轴线距离的最大值可以直观地反映出两装配体轴线的偏离程度以及两装配体坐标原点的位置偏离程度。 在理想装配情况下，{WP2}相对于{WP1}的z轴始终重合，装配体A与装配体B之间相对运动约束为装配体A沿着{WP2}的z轴做直线运动；{WP2}相对于{WP1}的约束姿态用式(1)所示的Z-Y-X欧拉角矩阵WP1RWP2表示：

WP1RWP2=RZ(α*)RY(β*)RX(γ*)

(1)

式中α*、β*、γ*表示理想装配情况下的{WP2}相对于{WP1}的Z-X-Y欧拉角。在实际装配情况下，WP1RWP2的Z-Y-X欧拉角分别为α、β、γ；当前两个装配体之间姿态变换的欧拉角与理想欧拉角的差值取绝对值求和可以明显地反映实际情况下与理想情况下两装配体之间的约束姿态的差别，装配姿态误差AtE的定义如式(2)所示：

AtE=|α-α*|+|β-β*|+|γ-γ*|

(2)

综上所述，装配位置误差的定义为：装配体A与装配体B坐标系的原点到理想装配轨迹线上距离的最大值；装配姿态误差的定义为：对当前装配体A与装配体B之间姿态变换的欧拉角与理想欧拉角差值的绝对值求和。在协调装配过程中，为了降低装配误差，提高装配成功率，主机器人主要实现直线插入运动，从机器人根据装配约束关系对主机器人运动所产生的装配误差做补偿运动。

2 基于B样条的关节轨迹规划模型

2.1 主-从机器人B样条关节轨迹的确定

主机器人末端在时刻ti处经过一系列指定的笛卡儿空间任务点Pi(i=0,1,…,n1)，在关节空间中经过关节插值点qi,1，采用累积弦长参数化方法将时间节点ti归一化为ui+k∈[uk,un1+k]。将ui+k代入关节轨迹表达式中，得到主机器人k次B样条轨迹曲线满足插值条件的n1+1个方程为：

(3)

B样条曲线的控制点数为n1+k，为求解控制点，还需附加k-1个方程，可以由切矢边界条件得到。设定主机器人在起始时刻的速度为vs1，加速度为as1，加加速度为js1；终止时刻的速度为ve1，加速度为ae1，加加速度为je1；当k=7时，附加方程如式(4)所示：

(4)

从机器人随主机器人的运动变化，根据装配约束条件确定从机器人末端的位姿，由逆运动学求得从机器人qi,2，得到从机器人经过的关节位置-时间节点序列。为了补偿主机器人B样条插值轨迹的误差，在主机器人B样条轨迹的时间节点区间内计算最大装配位置误差及此时刻主机器人的关节位置，并根据装配约束条件确定此时刻从机器人末端的位姿，由逆运动学求得从机器人新增的关节插值点qi,new与ti,new,i=1,2,…,nnew，其中nnew为总共新增插值点的个数，则从机器人经过的关节位置-时间节点序列如式(5)所示：

(5)

式中函数sort(x)表示对x进行非递减排序，并返回排序后的数组。随后同主机器人B样条关节轨迹确定方法，结合从机器人的归一化时间、附加方程、时间节点向量求得从机器人的B样条关节轨迹。

2.2 误差补偿策略

主机器人驱动装配体A从装配任务点Pi连续运动到Pi+1时，由于B样条插补运动会产生一定的装配位置误差，由此产生的装配阻力过大会使装配失败甚至损害重要部件。因此需要从机器人在装配约束下对主机器人的B样条关节轨迹进行补偿，补偿策略如下：

1) 根据主机器人的关节位置序列qi,1和时间序列ti(i=0,1,…,n1)，确定从机器人的末端位姿，由从机器人逆运动学确定相应的从机器人关节位置qi,2和时间序列ti(i=0,1,…,n2),n2=n1，令logo=0。

2) 在关节空间中利用从机器人关节轨迹的确定方法对从机器人经过的关节位置-时间节点序列进行插值，得到从机器人的关节轨迹；如果logo=0，则执行步骤3；否则输出主-从机器人B样条关节轨迹，算法终止。

3) 预设允许最大装配位置误差Ep,max和姿态误差为Ea,max。遍历从机器人B样条轨迹的时间区间[ti,ti+1],i=0,1,…，n2-1内的最大装配位置误差和姿态误差；若最大装配位置误差和姿态误差都小于Ep,max和Ea,max，令logo=1，则执行步骤2)；若最大装配位置误差和姿态误差不都小于Ep,max和Ea,max，则计算出此刻主机器人的关节位置，根据装配约束关系确定此时刻的{WP2}，对该区间内主机器人B样条插值产生的装配误差进行补偿。采用逆运动学求得该时刻从机器人新增的插值点qi,new与相应时刻ti,new,i=1,2,…，nnew,其中nnew为新插值点总数；并更新从机器人经过的关节位置-时间节点序列；执行步骤2)。

3 基于QPSO的协调装配轨迹优化

双机器人装配过程中，机械臂与障碍物之间以及机械臂与机械臂之间可能发生碰撞干涉。在实际操作中，通过人工示教操作可得到避障中间点，但是此避障中间点不一定是最优的避障位置，且会影响整个协调装配任务的完成时间及轨迹的平滑性。

通过调整主-从机器人避障点的位置，可以调整整个装配过程的时间、平均脉动以及判断是否发生碰撞。因此确定优化变量如式(6)所示：

(6)

整个双机器人装配轨迹优化过程如图2所示。首先，将已知的主-从机器人末端初始位置、过渡点、协调装配序列点映射到关节空间；然后根据示教的避障中间点以及搜索范围确定算法粒子搜索空间；随后，将两条轨迹进行B样条插值；最后结合目标函数和罚函数，利用QPSO算法搜索主-从机器人最优或者接近较优的避障点，从而得到最优或者接近较优的双机器人协调装配轨迹。

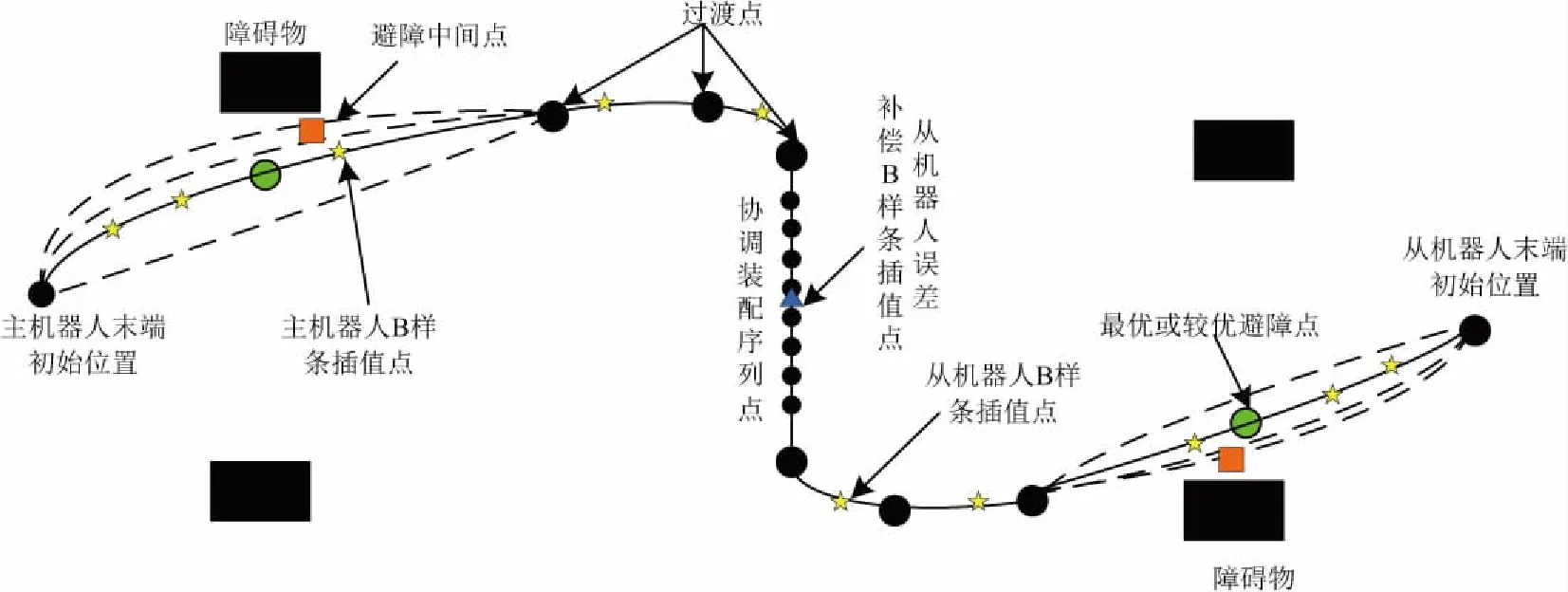
图2 双机器人装配轨迹优化过程示意图

利用QPSO求解双机器人协调装配中多目标优化轨迹问题的算法，实现步骤如图3所示。

图3 QPSO算法伪代码

4 仿真实例

4.1 仿真实验条件

以两个Staubli tx90工业机器人为实验对象，双机器人各需要避开1个障碍物后进行协调轴孔装配为例。基于Open Inventor环境，利用VC++6.0编程软件建立了双机器人协调装配的仿真平台。主-从机器人的初始时刻的关节位置都为(-90°,-20°,130°,0°,65°,0°)；通过示教操作双机器人得到主-从机器人的避障中间点处的关节位置都为(-90°，-45°，180°，0°，39°，0°)。设关节空间中对避障中间点处的关节搜索幅度δ=15，干涉检测点间距L=2.5mm。选取主机器人基坐标系为世界坐标系，主-从机器人的关节轨迹均由7次B样条曲线插值得到，在主-从机器人夹持工件的起始时刻和装配结束时刻的速度、加速度和加加速度均为0。不失一般性，取约束放大系数kv1、ka1、kj1、kv2、ka2、kj2均为2.9，预设允许最大位置装配误差Ep,max为0.01mm，预设允许最大姿态装配误差Ea,max为0.001°，权衡3个评价指标对优化目标函数的影响程度，取ω1、ω2、ω3均为1。通过主机器人的逆运动学将装配任务点转换到主机器人的关节空间中，得到装配任务的关节位置。从机器人经过的关节位置序列由双机器人协调装配轨迹规划策略得到。

4.2 仿真结果及分析

利用量子粒子群算法求解双机器人协调装配轨迹多目标优化问题，取粒子数为100，迭代150次，得到适应度函数如图4所示。

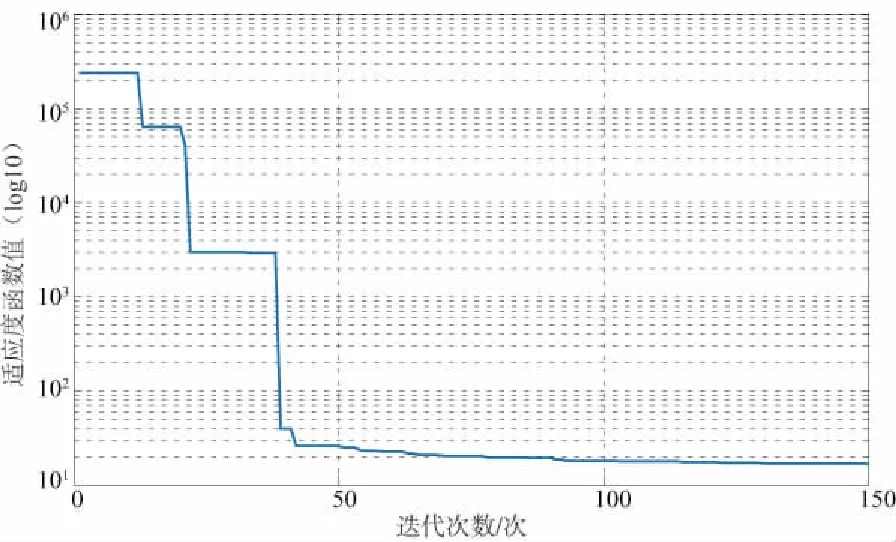
图4 适应度函数值

由图4可知，迭代初期适应度值快速下降，当迭代到第50次后，收敛速度减慢，逼近于最小值。采用QPSO算法规划出双机器人协调装配轨迹的最短执行时间为ft=13.0017s；平均脉动为fj=3.8219。

在装配过程中，假设将从机器人所夹持的装配体B保持静止，主机器人夹持的装配体A相对于静止的装配体B作直线插入运动，所形成的装配误差为单机器人装配误差。单、双机器人装配位置误差如图5(a)所示，单、双机器人装配姿态误差如图5(b)所示。

由图5可见，经过3个过渡点(单机器人位置、姿态误差图上的前3个误差值过0点)后，双机器人装配位置误差和装配姿态误差都接近于0。与单机器人装配机器人误差相比，双机器人协调装配误差明显小于单机器人装配误差。通过QPSO优化以及误差补偿得到的双机器人B样条关节轨迹驱动主-从机器人协调运动，可以使主-从机器人分别绕过障碍物、降低装配误差且以较优的轨迹高效地完成协调装配作业，从而验证了所提的双机器人协调装配轨迹规划方法的有效性和可靠性。

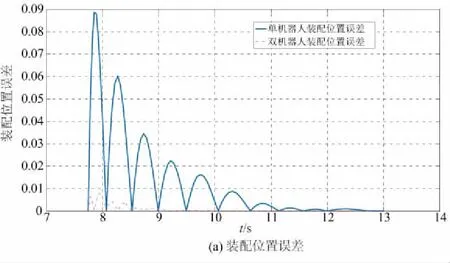
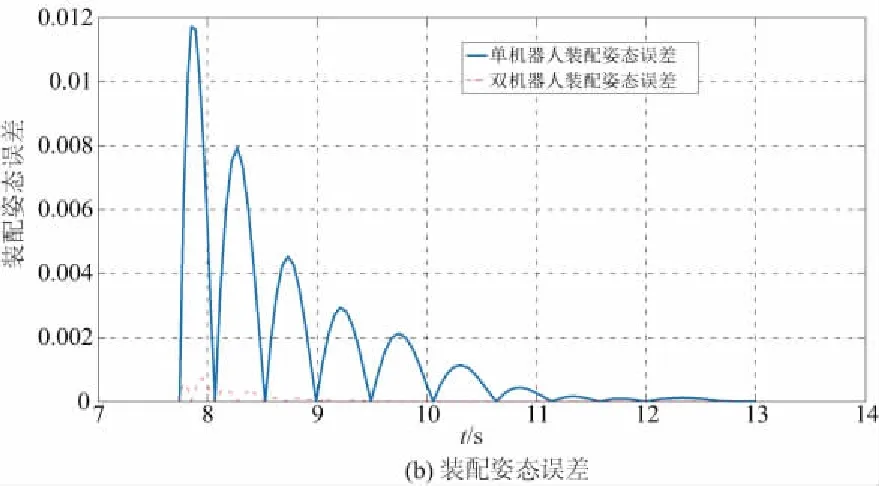
图5 单、双机器人装配误差

5 结语

结合QPSO和B样条提出一种双机器人系统的协调运动方案、避障算法、轨迹规划方法以及优化方法。该方法可以规划出一条避免碰撞干涉、执行时间较短、关节轨迹较为平滑、起始与终止的速度、加速度、加加速度可以任意配置的轨迹，并且降低了插值引起的误差。采用此方法所得到的轨迹保证了装配过程中主-从机器人驱动的稳定性、平滑性以及装配的高效率性。此外，该方法可以推广到多机器人协调装配、协同定位等问题的轨迹规划应用中，同时该方法有望集成到双机器人离线仿真软件中。