基于曲面配准的柔性件装配偏差分析
2020-07-16徐辉王志国
徐辉,王志国
(南京航空航天大学 机电学院,江苏 南京210016)
0 引言
装配偏差是指装配体实际装配尺寸与设计尺寸间的偏差,其受到制造精度与装配工艺等诸多因素的影响。LIU和HU[1]基于有限元法建立一维悬臂梁模型,并利用该模型分析了零件制造误差、夹具定位误差以及装配顺序对装配偏差的影响。由于一维模型的局限性,随后将该模型推广至三维,并将柔性件装配流程划分为4步:定位—夹紧—装配—释放回弹,在此基础上结合有限元法与统计学方法提出了著名的影响系数法(method of influence coefficient)。该方法通过构建敏感矩阵建立输入误差源与输出装配偏差的线性关系。随后针对柔性件装配偏差的研究多以“定位—夹紧—装配铆接—释放回弹”的装配仿真流程为基础,结合影响系数法与超元刚度理论构建力学模型[2-4]。然而,该方法在许多方面仍需改进与完善,其仅预测了装配体在装配夹具上的装配回弹偏差,而在实际装配过程中,装配体还需进行下架操作,在装配体内部残余装配应力的作用下,装配体会再次变形,因此传统分析模型求解得到的装配偏差对实际装配的指导作用有限。
本文对“定位—夹紧—装配铆接—释放回弹”装配仿真流程予以完善,通过添加“装配夹具完全释放”环节模拟装配体的实际下架,考虑到超元刚度矩阵理论在实际应用中存在的缺陷,利用总体刚度矩阵替代超元刚度矩阵进行装配偏差建模,依据基准点选取原则,利用曲面配准技术将装配夹具完全释放后的装配体与名义位置进行配准以求得装配偏差。最后对飞机壁板件模型进行仿真实验,通过数据对比说明模拟装配夹具完全释放环节对于装配偏差分析的必要性。
1 柔性件装配偏差计算框架
柔性件装配仿真流程可分为4步:定位—夹紧—装配铆接—释放回弹,但其未考虑实际装配过程中装配夹具完全释放后装配体会再次变形,因此需要在上述装配仿真流程的基础上添加装配夹具完全释放的仿真步骤,如图1所示。

图1 柔性件装配仿真流程
1) 零件定位:利用夹具对零件进行确定性定位,定位后零件与名义位置的偏差为VA、VB。
2) 装配夹紧:利用额外装配夹具强迫零件位移至名义位置,施加的装配力为FA、FB。
3) 装配铆接:在零件装配铆接点处进行装配铆接,使之成为一个装配体,此时装配体内部存在装配应力。
4) 释放回弹:释放装配夹具,装配体在回弹力的作用下发生回弹变形。回弹力FAB作用位置与装配力作用位置相同,大小相同,方向相反,与FA、FB存在线性关系,回弹偏差为VAB。
5) 装配夹具完全释放:为得到装配体下架后形状,通过释放掉一端确定性定位点约束模拟装配夹具完全释放,回弹力F′AB为确定端约束力反力,此约束力反力引起的回弹偏差为V′AB,释放一端确定位约束后装配体较名义位置的回弹偏差为V″AB。利用总体刚度矩阵理论建立如下装配偏差力学模型:
(1)
FAB=KABVAB
(2)
(3)
在装配夹具完全释放后,需要通过测量基准或人为定义的基准进行装配偏差计算。当测量基准或人为定义基准与其名义位置的对应点不重合时,需利用曲面配准技术进行配准。若装配体先进行旋转操作后进行平移操作,记旋转矩阵为R,平移矩阵为T,装配体某关键点的名义位置为p,下架后该点位置为p′,则装配偏差为:
=Rp′+T-p
(4)
2 装配夹具完全释放模拟
由于装配体模型在变形前后其对应点关系是唯一确定的,考虑装配偏差模型在采样点的偏差最小原则,建立基于最小二乘的曲面配准算法,通过SVD分解求解旋转矩阵和平移矩阵,进而获取装配偏差。
2.1 基准点选取
装配偏差的计算需要有参照基准的配合,在偏差测量中,基准的选择往往由人为设定,其与具体实际情况相关。在装配体回弹过程中,装配体的回弹量与装配体的刚度密切相关[5]。一般而言,装配体中装配零件数量越多的位置其刚度越大,在释放回弹及装配体下架阶段的回弹量较小。由于在装配过程中装配体在特殊位置会产生塑性变形,其在释放回弹及装配体下架阶段的回弹量极小,因此本文选取装配体模型中刚度较大及产生塑性变形的点作为基准点,建立对应的点集对。
2.2 设定目标函数
在上节中设置了基准点选取规则,记源采样点点集为S={s1,s2,…,sk},目标采样点点集为S′={s′1,s′2,…,s′k},则有:
s′i=Rsi+T+Ni
(5)
利用最小二乘法建立目标函数:
(6)
其中要求f最小。根据最小二乘求解法,可建立下式:
(7)
结合式(5)-式(7)即可求得旋转矩阵R与平移矩阵T。
2.3 基于SVD分解求解装配偏差
上节给出了目标函数与求解方法,但由于其求解过程过于繁琐,不易通过编程实现。本节将利用SVD分解对式(5)-式(7)进行求解。
目标约束函数f的物理含义为所有采样点与对应目标点间距离的平方和最小,表示如下:
(8)
记源采样点集S的质心为s,目标采样点集S′的质心为s′,则:
(9)
对式(8)进行展开,将式(9)代入可得:
(10)
由于式(10)中第1项与第2项均≥0,且第1项只和R相关,因此可先通过第1项求解R,再通过第2项求解T。
记源采样点对应去质心点坐标为qi,目标采样点对应去质心坐标为q′i,则:
(11)
式(10)可转化为:
(12)
则:
T=s′-Rs
(13)
展开式(12),记H为3×3的矩阵,其表达式如式(14)。由于R为正交矩阵,即RTR=I,则上式可转化为式(15):
(14)
φ=(maxtr(RH))
(15)
对H进行SVD分解,得:
H=UΣVT
(16)
则旋转矩阵
R=VUT
(17)
此时φ最大,利用式(17)即可求得平移矩阵T。
在求得满足最小二乘的R与T后,根据该变换矩阵对装配体整体进行刚性变换,通过式(4)即可获得装配偏差。
3 飞机壁板件装配算例验证
飞机壁板件是机身结构中最常见的装配体,其具有尺寸大、弱刚性、装配精度要求高等特点。由于装配过程中涉及到的零件较多、装配工艺流程复杂,导致预测壁板件的装配偏差难度较大[6-7]。本节针对壁板件利用有限元软件Abaqus及装配体偏差分析软件进行仿真,对比分析装配体下架环节对于装配体偏差分析模型必要性。
在CATIA中建立壁板件模型,如图2所示。两张蒙皮的理论曲率半径为1990mm,实际曲率半径分别为1995mm、1980mm,且该模型不考虑除蒙皮外的零件制造误差。蒙皮、长桁、角片及钣金框的材质均为铝锂合金,材料参数如下:泊松比为0.33,弹性模量为7.3×104N/mm2,蒙皮、角片厚度为2mm,长桁与钣金框厚度为1.6mm。下面针对壁板件模型处于释放回弹阶段与下架阶段的装配体偏差进行对比分析。

图2 壁板件结构示意图
将理论数模导入装配体偏差分析软件,并设置壁板件各零件的材料属性,根据表1中目标点误差源数据拟合出蒙皮对应的实际数模。随后根据表2、表3对壁板件进行边界条件设计、位移约束设置以及MPC绑定,如图3所示。
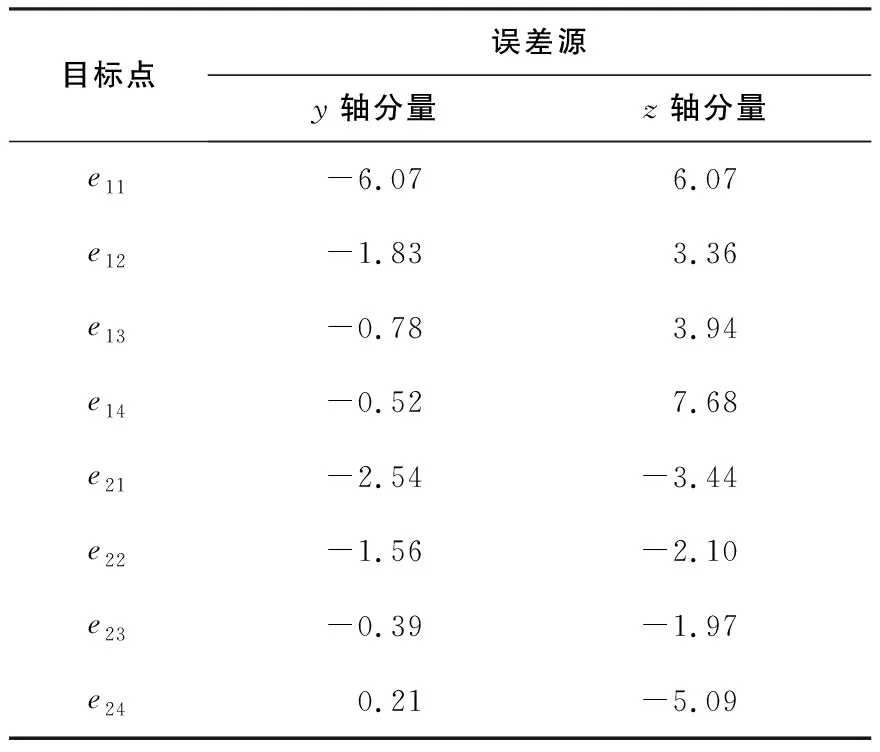
表1 目标点误差源 单位:mm
在设置完上述约束条件后,通过人为选取采样点和软件分析得到结果如图4所示。

图3 壁板件约束条件设置模型

表2 蒙皮过约束定位点初始偏差 单位:mm

表3 蒙皮装配铆接点初始偏差 单位:mm

图4 装配偏差对比折线图
对比图4中有、无装配体下架环节对应的折线图可发现,当无装配体下架环节与有装配体下架环节采用相同的参照基准时,最终得到的装配偏差仍具有较大的差别。其原因在于装配体下架阶段时,装配体再次发生了变形,模型中KPC点、铆接点及过定位点的相对位置发生了变化,当以确定性定位点作为基准匹配时,对应点处的偏差必然有所差别,这也验证了装配夹具完全释放模拟对于装配偏差分析的重要性。
4 结语
本文首先利用总体刚度矩阵建立柔性件装配偏差分析的力学模型,并通过释放一端确定性定位约束计算装配夹具完全释放后装配体的形状。然后依据装配体刚度大或塑性变形大的部位其回弹变形小的准则确定基准点的选取原则,通过最小二乘法确定曲面配准的目标函数,并利用SVD分解技术求解旋转平移矩阵,进而求解装配体的装配偏差。最后对飞机壁板件进行装配偏差分析,通过对比有、无“装配夹具完全释放”环节下关键点处的装配偏差,验证了装配夹具完全释放模拟对于装配偏差分析的必要性。
