压气机流道中砂粒轨迹及碰撞位置的计算方法研究

赵磊，刘璐璐，赵振华，陈伟

(南京航空航天大学 能源与动力学院，江苏 南京 210016)

0 引言

固体颗粒对压气机机匣、静子和转子叶片的冲蚀会造成永久性的磨损、点蚀和前缘破损，增加叶片表面粗糙度[1]和叶片通道的总压损失[2]，研究表明[3-4]叶尖间隙和表面粗糙度的增加所引起的叶片几何形状变化是影响压气机气动性能的主要因素。因此在对压气机进行抗冲蚀设计前，需要了解砂粒在压气机流场中受气流影响后的运动轨迹，并掌握其在相关部件上的碰撞位置，为压气机抗冲蚀设计提供参考。

早在20世纪80年代，国外已经开始对飞机防砂及抗冲蚀性能展开大量系统、深入的研究。GHENAIET采用Runge-Kutta-Fehlberg算法解决了砂粒的运动方程问题[4]，但是高阶Runge-Kutta-Fehlberg每一步计算右函数的次数和阶数相同，即在遇到复杂情况(多颗砂粒轨迹计算)时，会占用大量程序计算内存，同时该算法的局部截断误差估计比较复杂，使用固定时间步长计算在砂粒与壁面反弹处的轨迹，会使得局部误差波动较大，对运动轨迹求解造成更大误差，因而该研究方法还需进一步完善。孙露[5]以Visual C++为基础，采用颗粒轨道模型对风扇叶片流道中砂粒的飞行轨迹进行了研究，但未获得砂粒在叶片上的碰撞分布，对叶片相关部位所受的冲蚀损伤研究较少。

目前公开的文献对砂粒在压气机流场中飞行轨迹的研究还存在许多不足之处。根据有限的试验数据总结一个碰撞反弹的经验公式不能够对所有砂粒的反弹情况做出一个统一的描述，由于砂粒形状存在差异，碰撞后必然会出现远离公式计算结果的特殊情况，因而需要建立一个碰撞反弹数据库直接对试验结果数据进行插值调用。同时也需要得到一个在计算多颗砂粒运动轨迹时占用计算内存较少、迭代次数较低、拟合程度较高的计算方法。因此，本文针对第一级压气机流场，建立砂粒在流场中运动的数学模型，并通过对碰撞反弹数据库的调用与砂粒运动轨迹的数值模拟，揭示流场对砂粒运动轨迹的影响及砂粒在叶片上的碰撞规律。

1 计算方法

1.1 基本假设

本文的研究基于以下假设：1) 作为方法研究，为简化计算，本文砂粒选用质量均匀的圆球模型。2) 砂粒在运动过程不会发生破碎，也不会发生变形。3) 忽略砂粒对压气机内部定常流场的影响[6-7]。4) 在计算砂粒受力与碰撞时取质心为受力点。5) 不考虑叶片受到冲击后产生凹坑、鼓包、磨损。

1.2 运动轨迹求解步骤

单颗砂粒在压气机流场中运动轨迹的计算流程如图1所示。将压气机某一工况气动计算结果以及碰撞反弹试验数据导入数据库后，设置砂粒初始参数，根据单颗粒轨道模型，计算砂粒在每一时刻的受力和单位步长下的运动轨迹。根据碰撞反弹程序，在获得该步长下运动轨迹的同时进行壁面和叶片的碰撞判断，若发生碰撞则通过调用碰撞反弹数据库插值获得反弹参数，而后进行下一数值点的计算，直至砂粒飞出计算域。在结束当前砂粒的轨迹计算后程序立即将数据保存至数据库中，包括各计算步的位置、速度以及碰撞点位置、碰撞速度和碰撞角度，而后程序立即开始下一颗砂粒的轨迹计算。

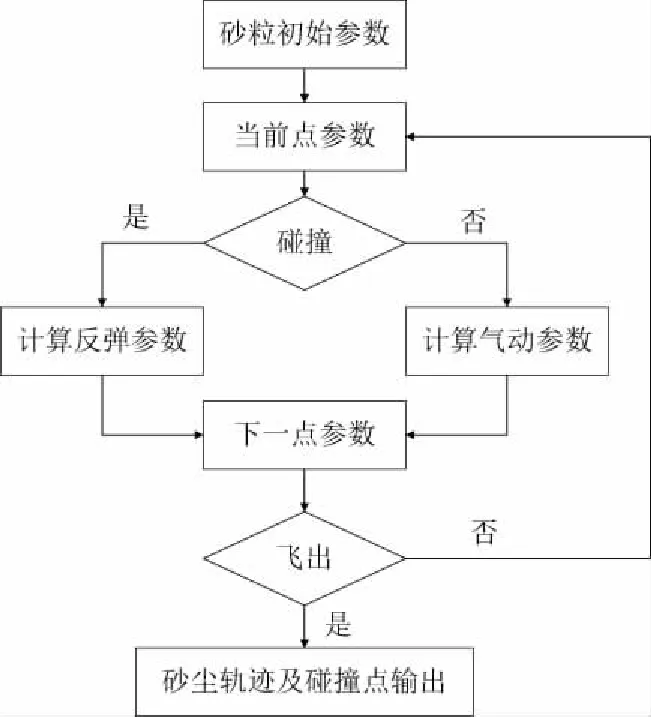
图1 单颗砂粒运动轨迹计算流程图

1) 受力分析与运动方程

根据牛顿第二定律[8]建立砂粒在流场中的受力运动方程F=ma，式中F为砂粒在流场中受到的合力，a为在当前条件下砂粒的加速度，m为球形砂粒的质量。要获得砂粒在压气机流场中的运动轨迹，首先要确定其在流场中所受合力。研究表明，球形砂粒在流场中主要受到气流曳力、压力梯度力与离心力的影响[9]，故本文也仅考虑这3个力对砂粒的作用。F=Fd+Fp+Ff，式中Fd为气动曳力，Fp为压力梯度力，Ff为离心力。其中Fd和Fp与砂粒所在位置的压力、密度、温度等因素有关，而这些气动参数仅存在于密集的网格节点上。因而要获得任意位置所受合力，必须首先分析压气机流场气动数据。在任意时刻下，考虑了网格点与砂粒位置的距离，采用加权平均方法，获得砂粒所在位置的压力、温度、密度等参数。本文采用球形搜索方法，以砂粒所在位置为圆心，搜索半径为R，如图2所示。

图2 球形搜索示意图

2) 碰撞反弹数据库的建立

碰撞反弹数据库的建立与调用对于求解砂粒与壁面、叶片发生碰撞后的运动轨迹以及提高程序计算效率发挥了极其重要的作用。砂粒的形状对碰撞后的反弹速度、角度有较大的影响[6]，作为初步分析，本文使用球形模拟分析结果[2]进行简化，部分数据如图3所示(因本刊为黑白印刷，如有疑问请咨询作者)，当碰撞反弹试验完成后再将所获得数据更新至数据库中。将碰撞反弹数据和流场参数按程序调用所需格式直接导入至数据库，当计算需要某个数据时直接查询调用，大大节省了计算内存，提高运行效率。

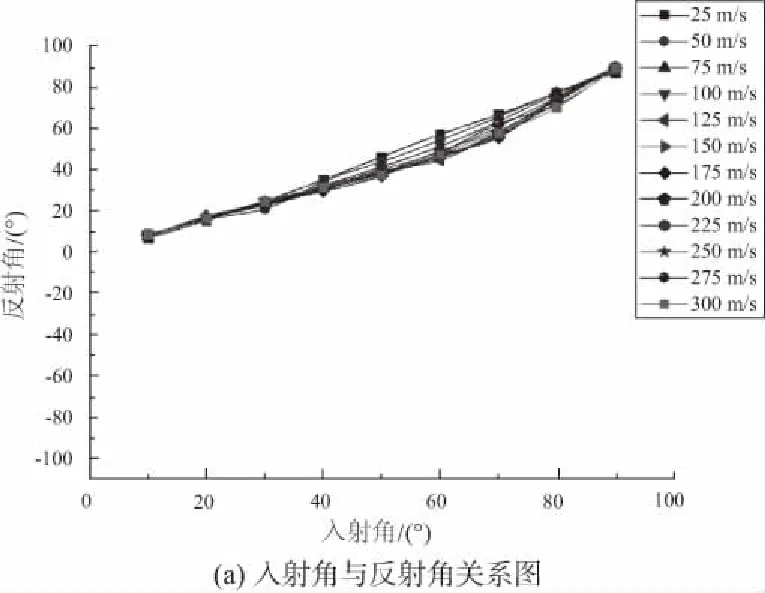
图3 不同入射速度下砂粒反弹参数

2 运动轨迹的数值计算分析

2.1 压气机进口参数设定

压气机流场的计算模型是基于某型轴流压气机进气部件建立的，包括导流叶片、转子叶片、机匣面与轮毂面。由于流道为周期对称结构，为了减少计算量，流场计算域选取包含一个完整导流-转子叶片的流道区域，如图4所示。计算域的上端面为外机匣内壁面，下端面为轮毂面，转子叶片绕轴向旋转。

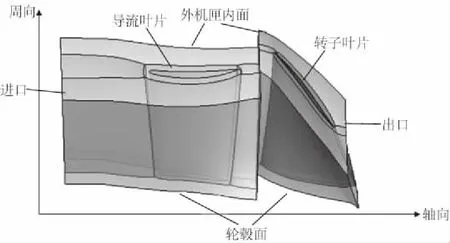
图4 单通道计算域

进口段砂粒初始条件设定选用已有的压气机入口砂粒分布数据，46%砂粒分布于80%及以上叶高处，其他砂粒在30%～80%叶高处分布较均匀，砂粒初始速度在100m/s左右。

2.2 砂粒运动轨迹的计算结果与分析

经过程序循环计算得到了所有砂粒的飞行轨迹图，选取其中部分典型砂粒轨迹如图5所示，砂粒从右端进入。导流叶片周围的砂粒运动轨迹以绝对坐标系表示，转子叶片周围的砂粒运动轨迹以相对坐标系表示。砂粒从压气机入口处飞入，保持原有速度进入导流叶片流场随气流沿轴向运动。由于周向初始速度较低，砂粒质量较小，约81.33%的砂粒通过气流不断加速飞入下一流场，剩余18.67%砂粒则与导流叶片前缘、叶盆等部位发生碰撞，飞行速度下降，运动轨迹发生偏离。转子叶片流场中，砂粒与叶片的相对速度远远大于其在导流叶片流场中的相对速度，因而更容易撞击叶片的压力表面。图5(b)中砂粒在转子叶片前缘和叶尖附近部位发生了较为密集的碰撞，由于转子叶片转速远高于砂粒的周向速度，很容易在叶片前缘与砂粒发生碰撞。初次碰撞造成了砂粒能量的损失，飞行速度降低，离心力在飞行中起主导作用，砂粒迅速向叶片尖端移动。

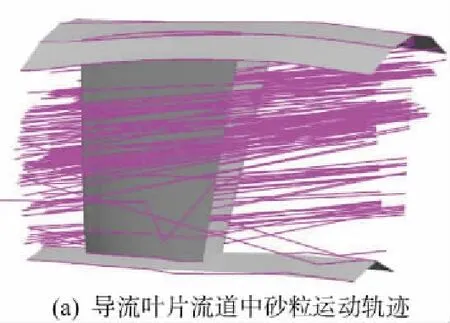
图5 砂粒飞行轨迹

图6为砂粒在叶片表面碰撞点的位置分布。图6(a)、图6(b)给出了叶片上碰撞点(灰色点)的疏密分布，图6(c)、图6(d)给出了砂粒在叶片表面各部位的撞击次数沿叶高、弦长的分布。

在图6(c)中，砂粒在导叶中的碰撞概率约为17.63%，碰撞点主要分布于叶片前缘、叶尖以及60%～100%叶高处。在图6(d)中，砂粒在动叶上的碰撞概率约为97.85%，碰撞点主要集中于70%叶高以上的位置。同时从图6(b)中也能看出，碰撞点在弦长方向上主要分布于叶片前缘位置。砂粒在叶片高度方向碰撞点的比例如图7所示，砂粒在70%及以上叶片高度处每隔10%叶高的碰撞概率均在10%以上。

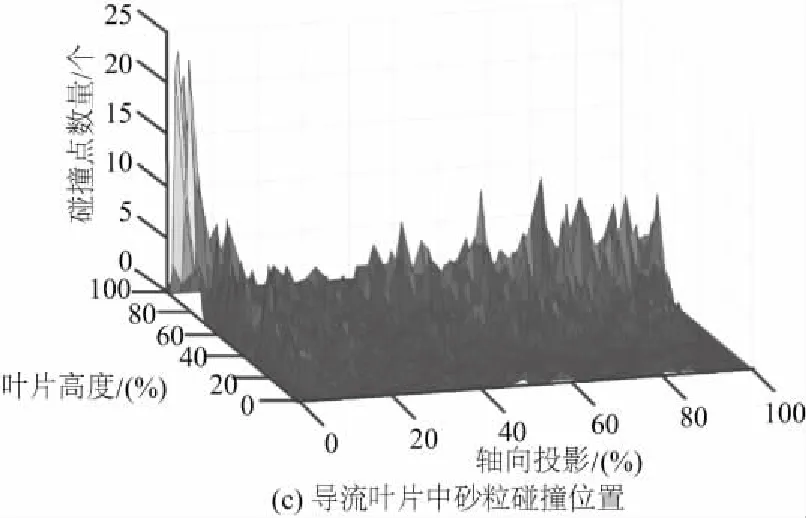
图6 砂粒碰撞位置

图7 动叶上砂粒在不同叶高处碰撞点比例

图8为砂粒在叶片碰撞位置处的速度分布。砂粒在导流叶片流场中随流特性较好，与导流叶片各个部位的碰撞速度较为接近(约为130m/s)。砂粒进入转子叶片流道后，由于叶片的飞速旋转与离心力的作用，砂粒在叶尖附近位置与叶片有极高的碰撞速度，随着叶片高度的降低，碰撞速度逐渐下降，其速率分布如图9所示，平均碰撞速度呈线性降低，从423.98m/s降至215.06m/s。同时由于在转子叶片的其他部位(顶端、前缘)也较为密集，因而这些部位受到的冲击损伤会更为严重。

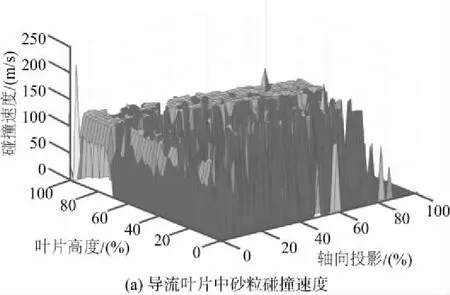
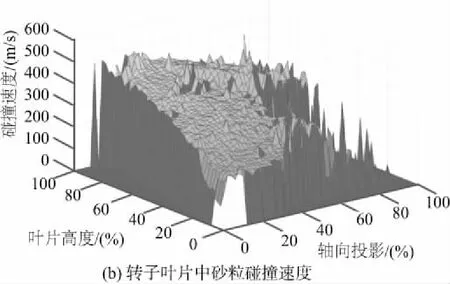
图8 砂粒碰撞速度

图9 动叶上不同叶高处碰撞速度

图10为砂粒与导叶、转子叶片各个碰撞部位的碰撞角度分布。砂粒在导流叶片流场中与叶片的碰撞概率较低，当发生碰撞时，碰撞角度在叶片弦长方向随着与叶片前缘距离的增加而降低。在转子叶片上，叶片前缘及叶尖附近位置的砂粒碰撞角度高达65°，而在其他部位的碰撞角度约为25°。叶片前缘及叶尖附近位置在该角度高速碰撞下使得在该部位叶片受到的冲蚀损伤更为严重[10]。

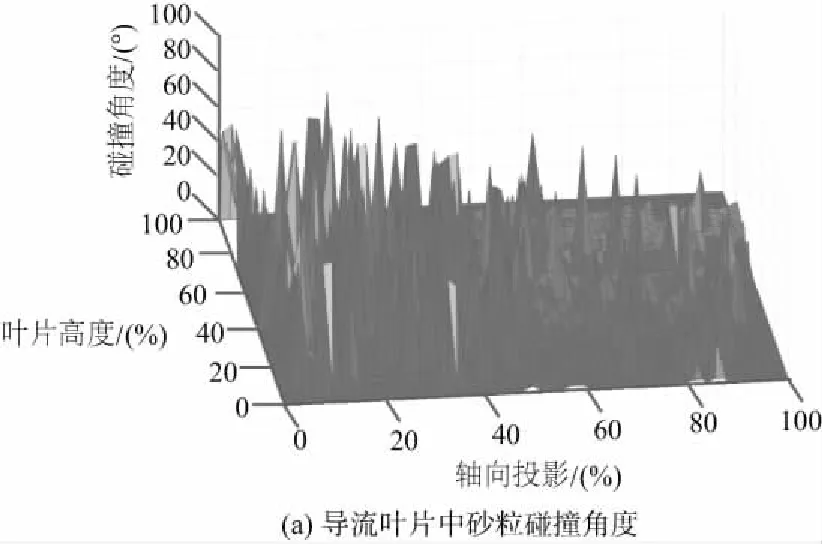
图10 砂粒碰撞角度

3 结语

本文通过对进入单级轴流压气机流道砂粒运动轨迹计算方法研究得到以下结论:

1) 导流叶片通道中砂粒运动速度在100～150m/s范围内，与叶片碰撞角低于60°。碰撞前后砂粒飞行速度变化较小，与叶片碰撞概率较低(约为18%)，对叶片造成的冲蚀损伤相对较小。转子叶片通道中，50%及以上叶高处砂粒与叶片的相对速度均在350m/s以上，而较低叶片高度的砂粒相对速度在220～350m/s内，叶片前缘及叶尖附近处碰撞角度较大(约为65°)。同时由于砂粒与叶片的碰撞概率较大(约为98%，特别是70%叶高以上位置及叶片前缘处)，对叶片造成的冲蚀损伤相对较大。

2) 利用单颗粒轨道模型结合数据库调用的方法对压气机流道中砂粒运动轨迹和碰撞位置数值模拟的计算效率较高。与现有研究结论相对比[11-12]，本研究方法计算结果趋势相同，误差较小。在数据库中碰撞反弹数据实时更新为可供调用的试验数据后，将大大提高计算精度，具有极高的实用性。针对不同型号的压气机乃至风扇、发动机，只需修改研究对象载入数据库中的流场参数、碰撞反弹参数以及模型参数即可直接编译获得砂粒飞行轨迹及碰撞位置，即可作为压气机内部砂粒运动轨迹及碰撞位置的研究方法。