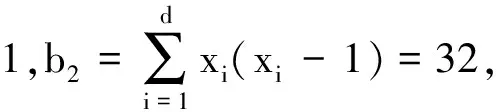区组传递2-(v,k,λ)设计与非点本原群ScwrSd
2020-07-15白舒伊彭莎丽甘凌方詹小秦
白舒伊, 周 涛, 彭莎丽, 甘凌方, 詹小秦
(华东交通大学 理学院, 江西 南昌 330013)
一个t-(v,k,λ)设计D定义为符合下列条件的有限关联结构 (P,E):
①P是v个点的有限集,P中的元素称为点;
②E是P的k-子集构成的集合,E中的元素称为区组;
③P中任意给定的t-子集都恰好包含在λ个区组中,其中λ≥1。

(1)
设计中的旗为一个点区组对(α,B), 其中α∈B。设g是P上的置换, 若B∈E当且仅当Bg∈E, 则称g为D的一个自同构。D的所有自同构关于映射的乘法构成一个群,记作Aut(D),并称其子群为D的一个自同构群。若D的一个自同构群G在E上传递, 则称G或D是区组传递的。点传递和旗传递都可类似地定义。关于2-设计更详细的理论, 可以参看文献[1-4],有关置换群论的理论和符号可参看文献[5-7]。
设D=(P,E)是一个具有自同构群G的t-(v,k,λ)设计。1967年,Block[8]证明了如果G是区组传递的, 那么G也是点传递的,也就是说G是对称群Sν的一个传递子群。Cameron和Praeger[9]证明了当t≥4时G是2-齐次作用在点集P上。因此,在非点本原的情况下,只需要考虑区组传递2-设计和3-设计。假设D是区组传递2-设计, 文献[10]中的命题1.1表明: 对于Sv中任意包含G的群H,设E*为H作用在区组上的轨道,则集合D*=(P,E*)是2-(v,k,λ*)设计,其中λ*≥λ。显然D*也是区组传递的, 且以H为自同构群。在非点本原的情况下, 非本原群ScwrSd是Sν的一个极大子群, 其中v=cd。因此, 如果存在一个区组传递且非点本原的2-(v,k,λ)设计,则一定存在一个以ScwrSd为自同构群的2-(v,k,λ*)设计。
本文研究非本原群ScwrSd区组传递作用在2-(v,k,λ)设计上(v=cd,30 由文献[10]中命题2.2可知以下引理成立。 引理1设D=D(c,d,x),v=cd,b1=k,则D是2-设计当且仅当 Delandtsheer和Doyen[11]证明了如果k是固定的且不允许有重复区组,则只有有限多对(D,G),其中G是区组传递且非点本原群。 引理4[4]设G是非平凡2-(v,k,λ)设计D=(P,E)的自同构群,则G在D上是旗传递当且仅当G是区组传递,且对任一区组B,群GB在B的点集上是传递的。 本文余下部分设D为2-(v,k,λ)设计,其中v=cd,G=ScwrSd在D上区组传递。 由引理3可知,下面可以假定2k≤v。文献[13]中已经完全分类了v≤30的情况,因此,本文只考虑30 命题1(v,k)∈{(34,12) (35,17) (36,7) (36,8) (36,14) (36,15) (39,19) (40,13) (40,14) (45,11) (45,12) (45,22) (46,10) (49,16) (49,17)}。 本部分给出满足命题1参数对(v,k)的2-设计的构造。 定理1所有满足条件的(D,G)都在表1中。 表1 满足2k≤v的所有(D,G) 续表vkb2bλxG36151847 029 2487 838 208(3,2,2,2,2,2,2,0,0)S4wrS93615181 114 767 360185 794 560(3,3,2,2,2,1,1,1,0)S4wrS93615189 437 1841 572 864(3,3,1,1,1,1,1,1,1)S4wrS9361518111 476 73618 579 456(4,2,2,2,1,1,1,1,1)S4wrS9361548576 108 28896 018 048(5,5,3,2)S9wrS4361548199 148 54433 191 424(6,3,3,3)S9wrS436153019 200 0003 200 000(3,3,3,3,3,0)S6wrS6361530259 200 00043 200 000(4,3,3,3,1,1)S6wrS6361530273 375 00045 562 500(4,4,2,2,2,1)S6wrS636153027 337 5004 556 250(5,2,2,2,2,2)S6wrS6391918168 880 14038 972 340(2,2,2,2,2,2,2,2,2,1,0,0,0)S3wrS1339191810 639 448 8002 455 257 420(3,2,2,2,2,2,2,1,1,1,1,0,0)S3wrS133919186 079 685 0401 403 004 240(3,3,2,2,2,1,1,1,1,1,1,1,0)S3wrS1339191816 888 0143 897 234(3,3,3,1,1,1,1,1,1,1,1,1,1)S3wrS13401344 729 753 600472 975 360(2,2,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0)S2wrS204013763 906 077 760390 607 776(8,5)S20wrS2401312156 764 16015 676 416(2,2,2,2,2,2,1,0,0,0)S4wrS104013122 786 918 400278 691 840(3,2,2,2,1,1,1,1,0,0)S4wrS1040131294 371 8409 437 184(3,3,1,1,1,1,1,1,1,0)S4wrS104013122 621 440262 144(4,1,1,1,1,1,1,1,1,1)S4wrS104013361 285 956 000128 595 600(5,4,2,2)S10wrS4401336370 440 00037 044 000(4,4,4,1)S10wrS4401316168 000 00016 800 000(3,2,2,2,2,2,0,0)S5wrS84013162 100 000 000210 000 000(3,3,2,2,1,1,1,0)S5wrS8401316262 500 00026 250 000(4,2,2,1,1,1,1,1)S5wrS840141435 389 4404 128 768(4,2,1,1,1,1,1,1,1,1)S4wrS104014144 180 377 600487 710 720(3,2,2,2,2,1,1,1,0,0)S4wrS10401414990 904 320115 605 504(3,3,2,1,1,1,1,1,1,0)S4wrS1040141433 592 3203 919 104(2,2,2,2,2,2,2,0,0,0)S4wrS10451110252 000 00014 000 000(2,2,2,2,2,1,0,0,0)S5wrS94511102 362 500 000131 250 000(3,2,2,1,1,1,1,0,0)S5wrS9451120426 746 88023 708 160(3,3,3,2,0)S9wrS54511201 851 776 640102 876 480(4,3,2,1,1)S9wrS5 续表vkb2bλxG4512242 160 406 080144 027 072(4,3,3,1,1)S9wrS5451224248 935 68016 595 712(3,3,3,3,0)S9wrS545121217 578 1251 171 875(4,1,1,1,1,1,1,1,1)S5wrS94512126 300 000 000420 000 000(3,2,2,2,1,1,1,0,0)S5wrS9451212393 750 00026 250 000(3,3,1,1,1,1,1,1,0)S5wrS945121284 000 0005 600 000(2,2,2,2,2,2,0,0,0)S5wrS94512423 108 480 375207 232 025(6,3,3)S15wrS34512422 840 672 835189 378 189(5,5,2)S15wrS34522423 600 000 000840 000 000(3,3,3,3,3,3,3,1,0)S5wrS9452242126 000 000 00029 400 000 000(4,3,3,3,3,2,2,2,0)S5wrS945224231 500 000 0007 350 000 000(4,3,3,3,3,3,1,1,1)S5wrS9452242472 500 000 0001 102 500 000 000(4,4,3,3,2,2,2,1,1)S5wrS945224275 600 000 00017 640 000 000(5,3,3,2,2,2,2,2,1)S5wrS9452284362 948 221 44084 687 918 336(6,5,5,4,2)S9wrS5452284188 195 374 08043 912 253 952(6,6,4,3,3)S9wrS5452284120 982 740 48028 229 306 112(7,4,4,4,3)S9wrS5461021 882 805 76081 861 120(2,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0)S2wrS2349163015 441 431 2501 575 656 250(3,3,3,3,3,1,0)S7wrS7491630166 767 457 50017 017 087 500(4,3,3,2,2,2,0)S7wrS749163072 060 012 5007 353 062 500(4,3,3,3,1,1,1)S7wrS7491630116 737 220 25011 911 961 250(4,4,2,2,2,1,1)S7wrS749163025 215 239 5742 572 983 630(5,2,2,2,2,2,1)S7wrS7491734277 945 762 50032 143 387 500(4,3,3,3,2,2,0)S7wrS7491734583 686 101 25067 501 113 750(4,4,3,2,2,1,1)S7wrS7491734210 126 996 45024 300 400 950(5,3,2,2,2,2,1)S7wrS7 证明这里仅考虑(v,k)=(35,17)的情形, 其余14种情况可通过类似的步骤证明。显然, (c,d)=(5,7)或者(7,5)。 x=(x1,x2,x3,x4,x5,x6,x7)=(3,3,3,3,3,2,0),(4,3,3,3,2,1,1),(4,4,2,2,2,2,1)或者(5,2,2,2,2,2,2)。 令G=S5wrS7为35个点集P上的非本原群,并且设Δ1、Δ2、Δ3、Δ4、Δ5、Δ6、Δ7为非本原块。取B⊂P使得当1≤i≤7时|B∩Δi|=xi。令E=BG, 由引理1知关联结构D=(P,E)是一个2-设计, 且G在D上区组传递。 如果x=(x1,x2,x3,x4,x5,x6,x7)=(3,3,3,3,3,2,0),那么在D中区组总数为 因此, 通过式(1)可得λ=9 600 000。 如果x=(x1,x2,x3,x4,x5,x6,x7)=(4,3,3,3,3,1,1), 那么D中区组的个数为 由式(1)易得λ=120 000 000。 如果x=(x1,x2,x3,x4,x5,x6,x7)=(4,4,2,2,2,2,1),那么D中区组总数为 由式(1)易得λ=90 000 000。 如果x=(x1,x2,x3,x4,x5,x6,x7)=(5,2,2,2,2,2,2),那么D中区组总数为 由式(1)易得λ=1 600 000。 如果x=(x1,x2,x3,x4,x5)=(4,4,4,4,1),那么在D中区组的总数为 由式(1)易得λ=12 005 000。 若x=(x1,x2,x3,x4,x5)=(5,4,4,2,2),那么在D中区组的总数为 由式(1)易得λ=77 792 400。证毕。 下面2个推论可由定理1和引理3得到。 推论1设G=ScwrSd是2-(v,k,λ)设计D的一个区组传递非点本原自同构群。如果30 推论2若G=ScwrSd在D上是旗传递的且30 ①D是一个2-(35,18,1 800 000)设计且G=S5wrS7; ②D是一个2-(36,8,33 750)设计且G=S6wrS6; ③D是一个2-(36,15,3 200 000)设计且G=S6wrS6; ④D是一个2-(39,20,4 330 260)设计且G=S3wrS13; ⑤D是一个2-(40,27,1 179 648)设计且G=S4wrS10; ⑥D是一个2-(40,14,3 919 104)设计且G=S4wrS10; ⑦D是一个2-(45,12,5 600 000)设计且G=S5wrS9; ⑧D是一个2-(45,12,16 595 712)设计且G=S9wrS5。 证明显然, 若G是旗传递的, 则G一定是区组传递的。因此,D是表1中的某一个设计或是其补设计。假设B是D中的一个区组,不失一般性,假定|B∩Δi|=xi≠0(1≤i≤n),且|B∩Δj|=xj=0(1 最后需要说明2-(35,18,1 800 000)设计是2-(35,17,1 600 000)设计的补设计;2-(39,20,4 330 260)设计是2-(39,19,3 897 234)设计的补设计;2-(40,27,1 179 648)设计是2-(40,13,262 144)设计的补设计。1 相关引理



2 主要结果
2.1 参数判定
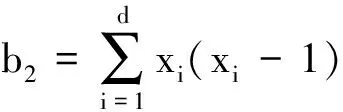
2.2 设计的构造