m-相依随机变量序列的中心极限定理及逼近速度
2020-07-15井照敬
井照敬
(巢湖学院数学与统计学院,安徽 巢湖 238000)
0 引言
中心极限定理最早在18世纪就被提出,是概率理论中非常重要的一类定理,并且在金融、网络通信和医学研究等领域被广泛应用.随着时间的发展,中心极限定理的研究也越来越深入,其研究对象也越来越广泛,由最初的独立随机变量到如今各种相依类型的随机变量.其中m-相依序列随机和渐近正态性的讨论也逐渐被一些学者提出[1-3],由此就得到了一些随机变量分布趋近于正态分布的逼近速度的问题,并且这个问题的讨论是由 Tomkó[4]和Sreehari[5]提出的.
近些年,我们关注到一些相依序列正态性逼近定理的文章,其中Prakasa Rao[6-7]分析了相依序列的渐近正态性,并运用柯尔莫哥洛夫距离计算其与正态分布的的逼近速度.本研究在此基础上对m-相依随机变量序列做了一些改善,并进一步讨论Nn的极限分布和对m-相依随机变量序列逼近速度的估计.
1 主要定义与定理
定义1.1[8]对于随机变量{Xn,n≥1},若存在一个整数m,和任意的n,j≥1,有(Xn+m+1,…,Xn+j)与(X1,…,Xn)独立.则称随机变量{Xn,n≥1}是m-相依的.特别地,当m=0时,随机变量{Xn,n≥1}是独立序列.
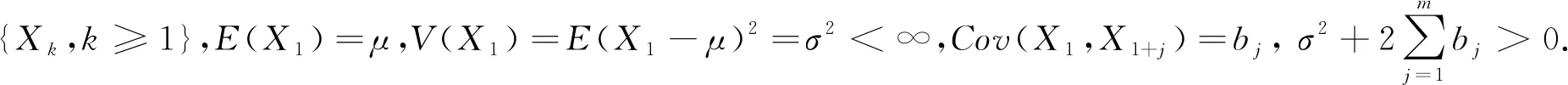
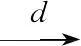
{Nn,n≥1}为一非负整数值随机变量序列,设其在n≥1时与随机变量序列{Xk,k≥1}独立,且Nn标准化后依分布收敛于随机变量Z2(Z2为标准正态随机变量).则:
(1)
其中Z*为随机变量Z1和Z2的线性组合.随后主要计算(1)式的逼近速度.下文中不同地方的C表示不同的正常数值.
2 假设和引理
假设非负的整数值随机变量序列{Nn,n≥1}满足:
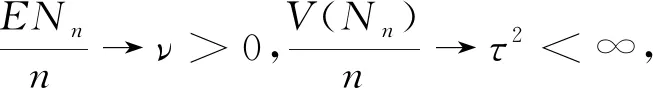
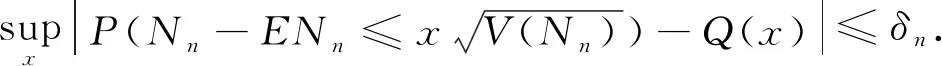
对于m-相依随机变量序列{Xk,k≥1},令Cov(X1,X1+j)=bj,在定理 1.2的条件下,当n>m时有:
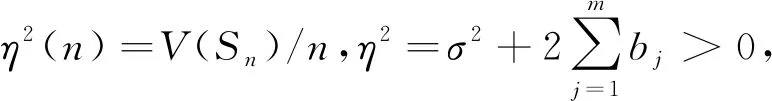
且在满足假设i)、ii)的情况下,亦有下列成立:



注记:结论②已被Prakasa Rao和Sreehari[6]证明,①、③易证.
定理2.1[10]令Φ(x)为标准正态随机变量的分布函数,若0<δ≤1时,E|X1|2+δ<∞,则

|P(Un+VG(Un)≤z)-P(U+cV≤z)|≤
3 结论和证明
下面,我们介绍一些符号.
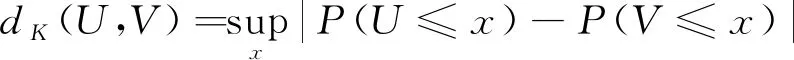
其中Z2服从假设ii)中给出的分布函数Q,同时与随机变量Z1独立.
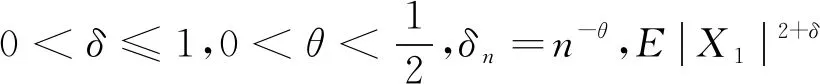
定理3.1的证明由三角不等式:
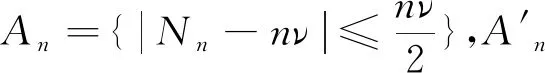
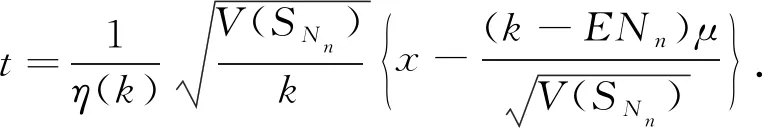
由切比雪夫不等式和定理2.1给出的边界,并对充分大的n可得
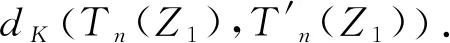
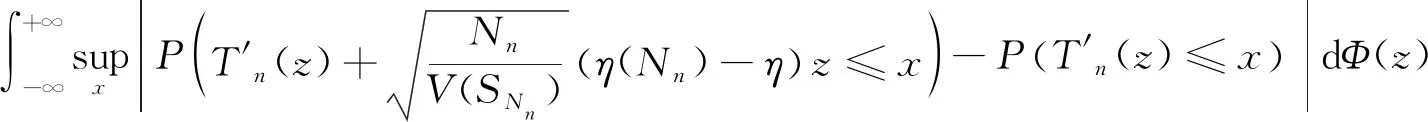
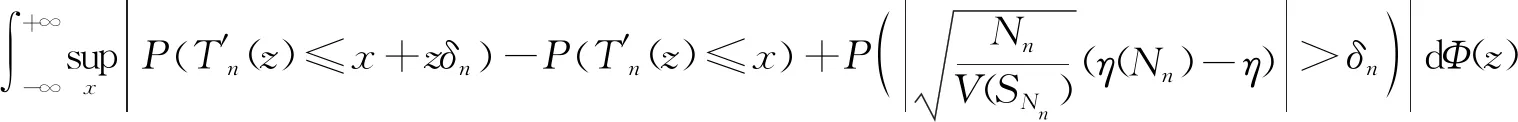
其中
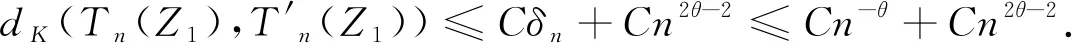
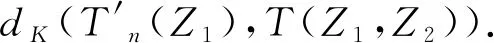
由引理2.1,可得

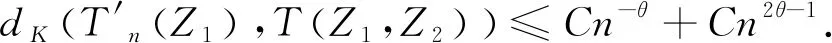
综上,由三角不等式可得
dK(Tn,T(Z1,Z2))≤
注记 i)Islak[12]获得了m-相依序列的中心极限定理但没有涉及逼近速度的计算.Prakasa Rao和Sreehari[6-7]分析了相依序列的渐近正态性,并运用柯尔莫哥洛夫距离计算其与正态分布的逼近速度.本研究在此基础上运用三角不等式进行分段估计,得到了m-相依序列的中心极限定理及其逼近速度.这是有一定实际意义的工作.
