完全判别信息Fisherfaces人脸识别算法

费经泰，程一元，查星星，王冬银

(1.安徽建筑大学城市建设学院基础部，安徽 合肥 238076；2.巢湖学院数学与统计学院，安徽 巢湖 238000)

0 引言

人脸识别是计算机模式识别中的一个重要领域，其中人脸识别中的特征提取至今仍然是一个重要的课题.常用的方法有：基于几何特征的方法、基于模型的方法、基于统计代数特征的方法.基于统计代数的方法通常把人脸图像转换成以像素值为元素的矩阵，并寻找一个最优变换将高维人脸空间矩阵降成低维的特征空间，从而提取人脸特征进行识别.由于易操作，实现简单等特点被广泛应用.比如著名的特征脸法(Eigenfaces)[1]，线性判别分析法(LDA)[2]等.特征脸法使用了PCA，经过PCA处理，从原始的人脸图像中得到了“本征脸”.LDA也是一种有效的特征提取方法，它的目的在于寻找一个最优判别矩阵，使得类间散度矩阵与类内散度矩阵的比值达到最大，即Fisher准则函数达到最大，并且在多数情形下，取得了比特征脸法更好的识别率.

但在实际应用的过程中，LDA经常出现“小样本问题”，即样本数n远远小于维数m，从而导致类内散度矩阵Sw为奇异阵，使得该方法失效.为了克服小样本问题，许多学者提出了改进方法，Belhumeur提出了Fisherfaces算法[2]，通过PCA降维，使得Sw可逆.但在对样本数据降维的过程中，丢失了部分判别信息.Chen等提出了零空间法(NLDA)[3]，发现Sw的零空间内存在大量的判别信息.但由于零空间的维数过高，从而不易计算.Yu提出了直接判别分析法(DLDA)[4]，同时对角化类内散度矩阵Sw和类间散度矩阵Sb，并在Sb的秩空间R(Sb)中寻找判别信息.但最终得到的判别信息并不包含Sw的零空间[5].

针对传统Fisherfaces算法存在的缺陷，本研究提出一种改进的Fisherfaces算法——完全判别信息Fisherfaces算法.通过把PCA降维过程中，全局散度矩阵St内被丢弃的特征向量加入到判别矩阵中，从而保证提取样本信息的完整性，并与上述传统算法进行比较，其识别率有一定的提高.

1 Fisherfaces算法

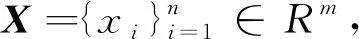
(1)

(2)

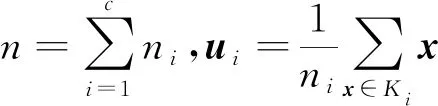
(3)

则LDA的目标是找一个最优判别矩阵Wopt，使得

(4)

易证Wopt是满足方程SbW=λSwW的解，即由Sw-1Sb的前d个最大特征值所对应的的特征向量所组成.并且有R(Sb)≤k-1，R(Sw)≤n-k，R(St)≤n-1，其中R(·)表示矩阵的秩.故该方法最多只能得到k-1个判别特征.

Belhumeur提出的Fisherfaces算法，克服了Sw奇异问题，该算法分为两步骤：第一步用St的列空间进行PCA降维，使得类内散度矩阵Sw非奇异，第二步用传统的LDA方法求解.整个算法描述如下：

步骤1：PCA阶段.对St作特征值分解：UTStU=Λ，其中U是非零特征值对应的特征向量组成的酉矩阵，满足UTU=I.Λ为对角矩阵，对角线上的元素为St非零特征值，取前t个最大非零特征值所对应的特征向量组成变换矩阵U1.

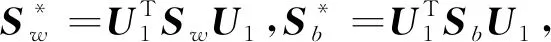
则最优判别矩阵为

Wopt=U1V

(5)

同样该算法最多也只能获得k-1个判别特征.

2 Fisherfaces(UD)和Fisherfaces(OD)判别矩阵

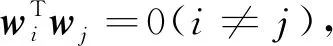
步骤1：计算

(6)

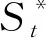
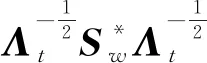
(7)

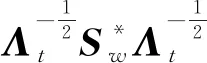
步骤3：令

(8)

则有

(9)

(10)

(11)

易知Z是可逆阵，且有

(12)

(13)

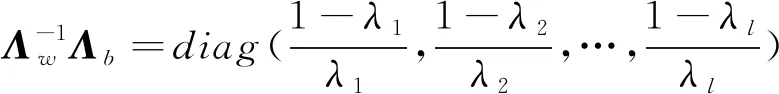
(14)

为了使判别矩阵Wopt是正交矩阵，对矩阵V作QR分解V=QR，Q为正交阵，R为上三角矩阵.则U1Q为Fisherfaces算法的OD矩阵，这里把它称作Fisherfaces(OD)判别矩阵，并记作

(15)

3 完全判别信息Fisherfaces算法

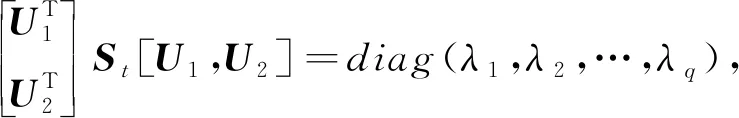
(16)

(17)

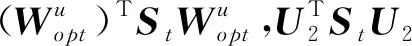
(18)

(19)

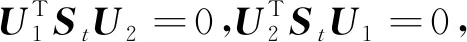
(20)

(21)

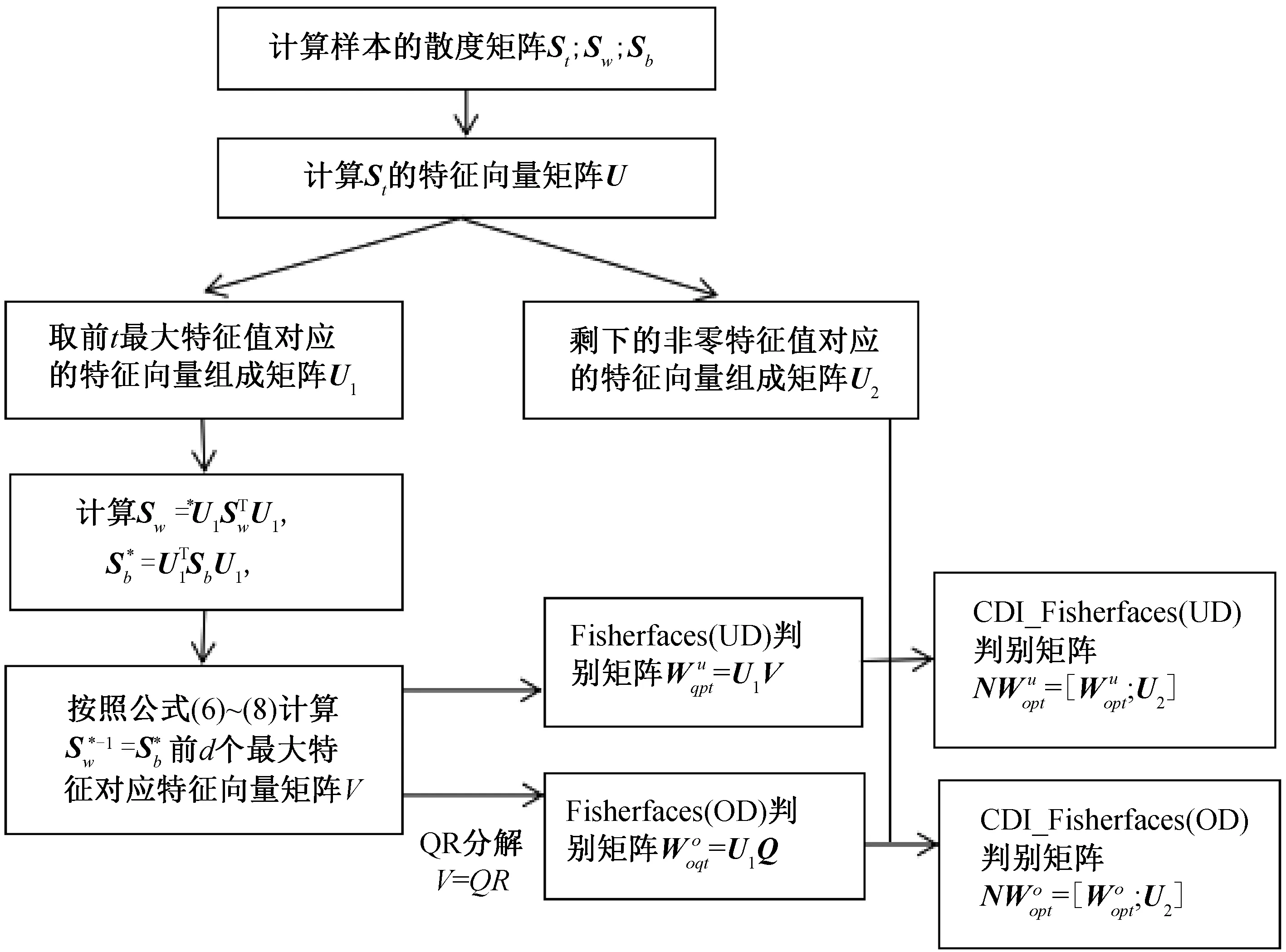
图1 CDI_Fisherfaces算法流程图

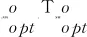
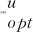
3.2 CDI_Fisherfaces算法综上所述，给出完全判别信息Fisherfaces算法(CDI_Fisherfaces)流程图如图1所示.

4 实验结果和讨论

为了验证本文中算法的有效性，分别在ORL人脸库和YALE人脸库进行测试，ORL人脸库包含40个人400幅图像，每人10幅图像，图像的大小为112×92.YALE人脸库包含15个人165幅图像，每人11幅图像，图像的大小为100×100.图2和图3分别显示了ORL和YALE人脸库中部分图像.其中每人随机选取k(k=2,3,4,…,8)幅图像作为训练集，剩下的作为测试集.每次实验运行30次，计算平均正确识别率.算法PCA阶段中，主成分的个数t取min(n-k,R(Sw)).所有算法取最大特征数，即ORL为39，YALE为14.识别过程采用最近邻分类器进行分类.

图2 ORL人脸库部分样例

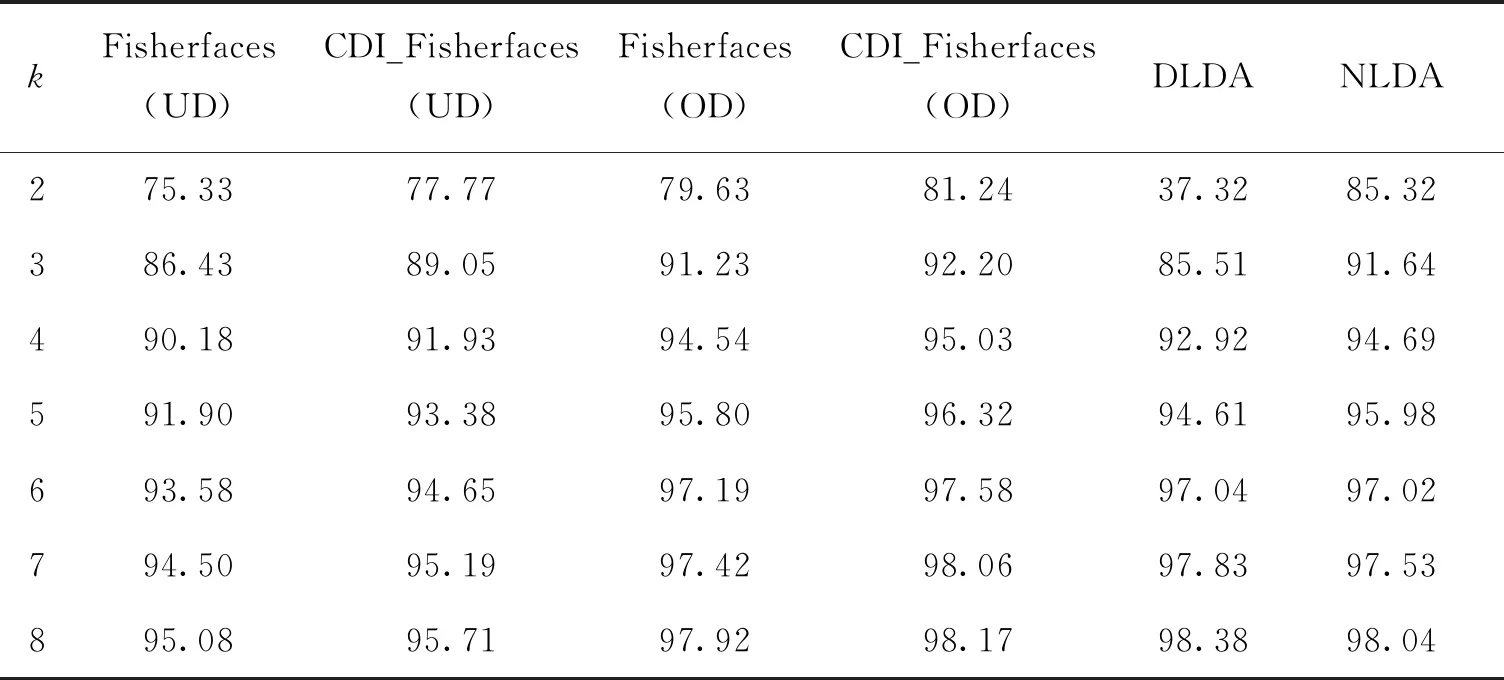
表1 不同算法在ORL人脸库上的识别率 %

图3 YALE人脸库部分样例

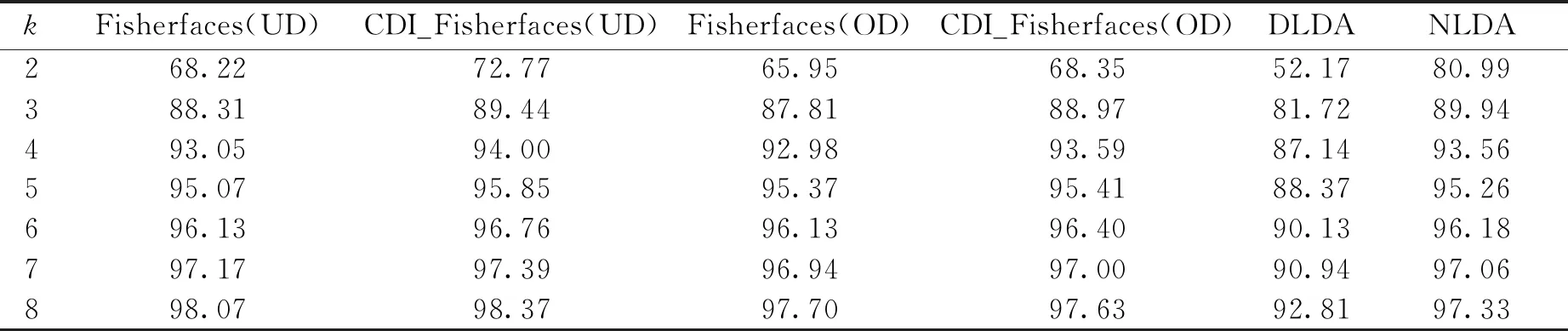
表2 不同算法在YALE人脸库上的识别率 %

从表1可以看出在ORL人脸库上，CDI_Fisherfaces(UD)和CDI_Fisherfaces(OD)识别率分别高于Fisherfaces(UD)和Fisherfaces(OD)，说明传统Fisherfaces算法在PCA阶段丢弃的特征向量包含有用的判别信息.当k的取值在3～7之间时，改进后Fisherfaces算法(CDI_Fisherfaces(UD)、Fisherfaces(OD)和CDI_Fisherfaces(OD))比传统的Fisherfaces算法(Fisherfaces(UD))取得了更高的识别率，其中CDI_Fisherfaces(OD)的识别率最高，原因在于其判别矩阵满足正交性，并且识别率高于直接判别分析法(DLDA)，零空间法(NLDA).当k=2时，由于训练样本非常少，所以NLDA算法的识别率高，当k=8时，由于训练样本比较充足，此时DLDA算法的识别率明显占优.

从表2可以看出在YALE人脸库上，同样可以看到完全判别信息的Fisherfaces算法(CDI_Fisherfaces算法)识别率要高于传统的Fisherfaces算法.但当判别矩阵满足正交性时，其识别率并不是最高.当训练样本数量较少时(如k=2和3)，NLDA算法的识别率较高，随着样本数的增加，CDI_Fisherfaces(UD)的识别率要略高于其他算法.

5 结束语

首先对传统的Fisherfaces算法的判别矩阵进行了分析，发现其判别矩阵具有统计不相关性，并针对传统Fisherfaces算法的缺陷，提出了一种完全判别信息的Fisherfaces算法，同时给出了CDI_Fisherfaces(UD)判别矩阵和CDI_Fisherfaces(OD)判别矩阵，最后通过在ORL人脸库和YALE人脸库上实验，取得了较好的识别率，说明了本文中提出的算法的有效性.