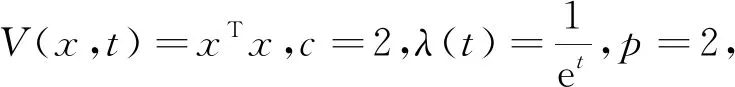无穷时滞脉冲随机泛函微分方程一般衰减意义下p阶矩稳定性
2020-07-15余国胜
余国胜
(江汉大学数学与计算机科学学院,湖北 武汉 430056)
0 引言
无穷时滞泛函微分方程理论的发展主要取决于相空间的选取.Hale和Lune[1]研究了无穷时滞泛函微分方程.考虑随机环境干扰,以及时滞在系统中无处不在,例如生物系统、物理系统、信息科学,在实际系统中,时滞还存在于系统状态的导数项中,这样的系统称为中立型系统.中立型系统受到人们广泛关注.吴付科等[2]讨论了无界时滞中立型随机泛函微分方程的Razumikhin-Type定理.谷海波和高彩霞[3]得到了基于Razumikhin-Type理论的中立型随机切换非线性系统的p阶矩稳定性和几乎必然指数稳定性.众所周知,脉冲有时存在于随机系统,朱全新[4]得到了马尔科夫调制脉冲随机泛函微分方程p阶矩指数稳定性.余国胜[5]考虑了Markov调制的无穷时滞脉冲随机泛函微分方程一般衰减意义下p阶矩和几乎必然稳定性.本文中研究无穷时滞脉冲随机泛函微分方程,与文献[5]不同,得到了一般衰减意义下p阶矩稳定性的新结果.
1 预备知识
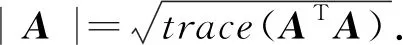
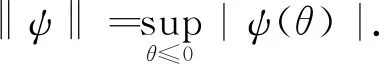
(1)
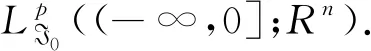
f:BPC((-∞,0];Rn)×R+→Rn,g:BPC((-∞,0];Rn)×R+→Rn×m是两个Borel可测函数.对于解的存在唯一性,我们作如下假设
假设1.1[6]函数f(xt,t)和g(xt,t)均满足Lipschitz条件和线性增长条件,即对∀t≥0,∀φ,ψ∈BPC((-∞,0];Rn),存在L>0使得
|f(φ,t)-f(ψ,t)|2∨|g(φ,t)-g(ψ,t)|2≤L‖φ-ψ‖2,
对∀t≥0,∀ψ∈BPC((-∞,0];Rn),存在K>0,使得
|f(ψ,t)|2∨|g(ψ,t)|2≤K(1+‖ψ‖)2.
定义1.1[6]λ∈C1(R+;R+),λ′(t)<0,λ(0)=1.且当t→∞时,有λ(t)→0.另外对于所有的t,s≥0,λ(t+s)≥λ(t)λ(s).
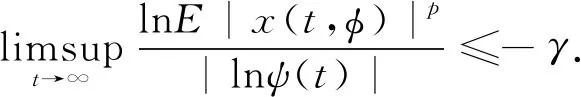
当p=2时,称为均方ψγ稳定,当ψ(t)=e-t时,称为p阶矩指数稳定,当ψ(t)=(1+t)-1时,称为p阶矩多项式稳定.
对于系统(1),任给函数V(x,t)∈C2,1(Rn×R;R+),定义微分算子
2 主要结果
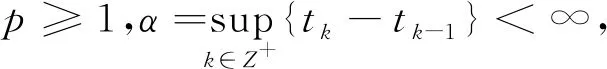
和Lyapunov函数V(x,t)∈C2,1(Rn×R;R+)有
a)c1|x|p≤V(x,t)≤c2|x|p;
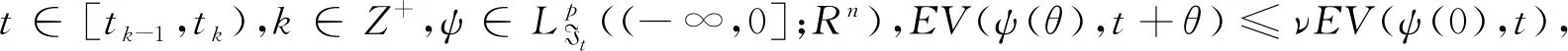
E|x(t,φ)|p≤M‖φ‖pλ(t),t≥t0.
定理2.1的证明由数学归纳法往证:
EV(x(t),t)≤M‖φ‖pλc(tk),t∈[tk-1,tk),k≥1
(2)

c2‖φ‖p=M‖φ‖pλ2c(α)≤M‖φ‖pλc(α)≤M‖φ‖pλc(t1)
(3)
假设(2)式对于k=1不真,令
s1=inf{s∈(t0,t1),EV(x(t),t)>M‖φ‖pλc(t1)},
由于EV(x(t),t)在(t0,t1)内连续,则有
EV(x(s1),s1)=M‖φ‖pλc(t1),EV(x(t),t)≤M‖φ‖pλc(t1),∀t∈(t0,s1).
事实上
EV(x(t0))≤c2‖φ‖p.
由(3)式可令
s2=sup{s∈[t0,s1),W(s) 由于W(t)在(t0,t1)内连续,则有W(s2)=c2‖φ‖p.由此可得 c2‖φ‖p≤EV(x(t),t)≤M‖φ‖pλc(t1),∀t∈[s2,s1]. 对于θ≤0,t∈[s2,s1],注意ν的定义有 由条件b),对于∀t∈[s2,s1], 定义D+E[λ(t)V(x(t),t)]=λ′(t)EV(x(t),t)+λ(t)ELV(xt,t),这里D+是Dini微分.定义如下 其中,χ:R→R是一个连续函数,故有 D+E[λ(t)V(x(t),t)]≤(1-c)λ′(t)EV(x(t),t), 对于∀t∈[s2,s1), 于是 (4) 与(4)式矛盾,则(2)式当k=1时成立.假设(2)式对于k=1,2,…,m成立,即 EV(x(t),t)≤M‖φ‖pλc(tk),∀t∈[tk-1,tk),k=1,2,…,m (5) 往证(2)式对于k=m+1仍然成立.由条件c)和(5)式有 (6) 若(2)式对于k=m+1不真,存在一个常数u∈[tm,tm+1),使得EV(x(u),u)>M‖φ‖pλc(tm+1).由(6)式u≠tm.定义u1=inf{u∈(tm,tm+1),EV(x(t),t)>M‖φ‖pλ(tm+1)}. 由于W(t)在区间(tm,tm+1)内是连续的,则有 EV(x(u1),u1)=M‖φ‖pλc(tm+1),EV(x(t),t)≤M‖φ‖pλc(tm+1),∀t∈[tm,u1]. (7) 对于∀t∈[u1,u2],θ≤0,由ν的定义有 和(4)式类似,有 (8) 与(8)式矛盾,对于k=m+1,(2)式成立,故有 注本文中条件b)与文献[5]中条件(3.1a)是完全不一样的,脉冲在系统的稳定性中起到了十分重要的作用. 本节通过一个具体的算例验证上一节主要定理的有效性.考虑n维无穷时滞中立型脉冲随机非线性系统 (9)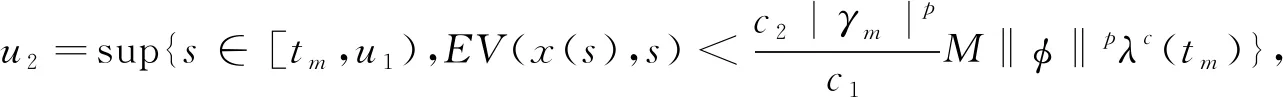
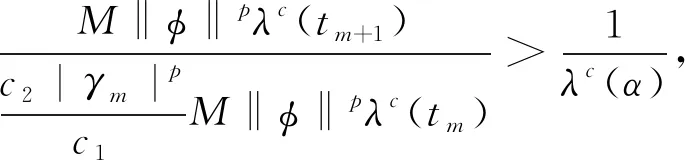
3 一个实例