基于证据理论和直觉模糊集的煤矿应急决策方法

张宇春，蒋 艳 ZHANG Yuchun， JIANG Yan

（上海理工大学 管理学院，上海 200093）

(Management School, University of Shanghai for Science and Technology, Shanghai 200093, China)

0 引 言

煤炭是我国主要能源之一，在煤矿开采的过程中不时会发生一些灾害事故，主要有瓦斯爆炸、塌陷、透水等，给国家和社会造成了巨大的财产损失和人员伤亡，当煤矿灾难事故发生时，救援能力的强弱以及合适的救援方案决定了救援成效。

考虑到煤矿事故发生时环境具有复杂性，时间紧迫性，在决策信息具有模糊性的情况下，多数学者在模糊集的基础上展开研究。例如，靖可等[1]在煤矿应急决策中使用模糊层次分析法确定属性权重，并提出整体优势度概念，实现备选方案与理想方案间的距离识别和最优决策。韩晋平等[2]对煤矿事故特点进行了详细分析，并提出了煤矿应急救援能力的模糊综合评价方法。由于直觉模糊集比模糊集描述问题更加的细腻全面，事实上，由于救援信息的不完全、个人认知的局限或方案里含有一些不完全的信息等，评估专家在决策过程中往往存在一定的犹豫性，所以将直觉模糊集引进煤矿应急救援决策中。陈孝国等[3]提出了属性权重未知，基于直觉模糊集对煤矿应急能力进行评价与研究。杨乃定等[4]提出了一种基于直觉模糊软集的煤矿应急救援决策方法，再利用推广的TOPSIS 方法对方案进行排序。陈孝国等[5]提出了基于直觉模糊集的煤矿突发事件应急救援TOPSIS 群决策模型，属性权重采用直觉模糊熵确定。杨悦等[6]为进一步完善煤矿应急救援能力评价方法并提高其可靠性，提出基于梯形模糊集熵权法的煤矿应急救援能力的效用值评价模型。

目前大多数学者所构建的评价指标体系中考虑到的因素较为全面，考虑到煤矿事故发生时的不确定性及信息的模糊性，大多数学者都使用直觉模糊集来处理。考虑到证据理论在处理不精确偏好与模糊信息方面的优势，又由于证据理论与直觉模糊集之间存在着本质的联系，目前没有发现学者将证据理论与直觉模糊分析法结合起来应用在煤矿应急救援决策上，本文使用证据理论将煤矿应急救援的信息进行融合并结合直觉模糊集解决决策过程中的不确定性及信息模糊性问题。

1 基本理论

1.1 证据理论

定义1[7]设 Θ 为识别框架，如果集函数Mass：2Θ→［0，1 ］满足m（Ø ）=0 并且有则称函数m 为识别框架Θ 上的Mass 函数。当A∈Θ，且m（A ）＞0 时，称 A 为焦元。

定义2[7]设Θ 为识别框架，m 为识别框架Θ 上的Mass 函数，∀A，B∈Θ，则由BeI（A定义的函数BeI: 2Θ→［0，1 ］称为 Θ 上的信任函数。由定义的函数PI：2Θ→［0，1 ］为 Θ 上的似然函数。

定义 3[7]假设 BeI1，BeI2，…，BeIn是同一识别框架 Θ 上的信任函数，m1，m2，…，mn为其相对应的 Mass 函数，那么有：

其中：k 为冲突系数。

1.2 直觉模糊集

定义4[8]设X 为一个给定的论域，则论域X 上的直觉模糊集可以定义为：

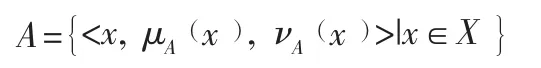
其中：μA（x ）:X→ ［0，1 ］，νA（x ）:X→ ［0，1 ］，满足∀x∈X， 0≤μA（x ）+νA（x ）≤1，μA（x ）和 νA（x ）分别为X 中的元素x 属于A 的隶属度和非隶属度。πA（x ）=1-νA（x ）-μA（x ）为集合A 中元素x 的直觉指数，亦称为犹豫度，即元素x 属于集合A 的不确定程度。

根据证据理论，直觉模糊集A 可以改写为A= ｛＜x， BIA（x ）＞|x∈X ｝，BIA为信任区间，BIA（x ）= ［BeIA（x ）， PIA（x）］，BeIA（x ）=μA（x ），PIA（x ）=1-νA（x ）。

2 基于证据理论的直觉模糊决策模型

2.1 问题描述

对于一个属性权重与专家权重未知的多属性群决策问题，专家集Pk（k=1，2，…，K ）由K 位专家组成，由n 个可行方案x1，x2，…，xn，m 个评价指标 （属性） o1，o2，…，om，分别构成方案集 X 和属性集 O。若专家 Pk对可行方案 xj∈X 在评价指标 oi∈O 下的评价值用直觉模糊数来描述，分别表示为专家Pk对可行方案xj关于属性oi隶属度（满意度），非隶属度（不满意度），犹豫度（不确定度），并且有得到专家P的直觉模糊决策矩阵Dkk

本文将决策系统的指标体系作为一组证据信息，基本的模型构建思路主要是利用记分函数和属性的不确定度来构建各证据下不同方案的Mass 函数，并运用D-S 证据理论进行信息融合， 最后得出决策结果。

Chen 在1994 年首次提出记分函数， 表达支持程度与反对程度的差值， 该值表示净支持程度。

定义5[8]对于直觉模糊数其记分函数为对记分函数进行归一化处理，得到初始记分函数矩阵

使用证据理论进行决策时，需要得到各证据下不同方案的Mass 函数，而求解属性的不确信度是一个关键点，本文使用灰色关联法求解属性的不确信度。

定义6[9]属性的q 阶不确定度可定义为其中为灰关联度，q 为不确定阶数，为了提高分辨效果，这里采用欧氏距离而不采用Hamming 距离，取q=2，ξ 一般取0.5，

这部分的Mass 函数赋值给识别框架Θ 本身，可以得到属性关于整体不确定性的Mass 函数（Θ ），整理如下：

2.2 属性权重处理

2.2.1 应急决策中属性权重计算。在突发的应急救援环境下，决策者掌握的信息往往是不确定的、模糊的。本文采用改进的直觉模糊熵计算公式[10]，充分考虑到应急决策信息的模糊性和决策者的犹豫度，在很大程度上能减少由于决策者主观性对决策结果造成的影响。计算公式如下：

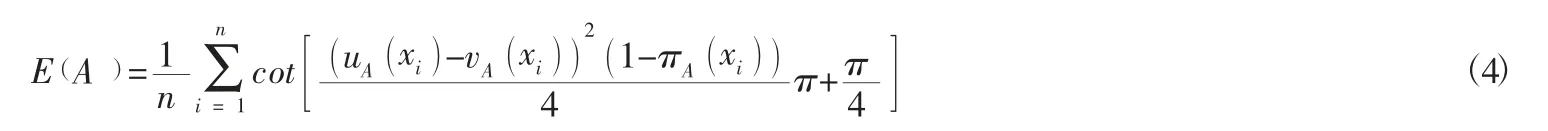
那么有第k 个专家的第i 个属性的权重为：

2.2.2 属性集证据的修正与合成。在构建Mass 函数后，采用合成规则对证据信息进行合成，为了保证每个证据信息处于同样的重要程度，避免由信息的不可靠而造成证据之间重要程度的差异，则需要对Mass 函数进行修正。

定义七[8]若e1，e2，…，en为识别框架 Θ 上的n 条证据，m1，m2，…，mn是与其对应的Mass 函数，称 φ （mi）为第i 条证据的综合重要程度，如果

那么称ej为关键证据，其他证据关于ej的证据权为根据证据权相关的算法，对 Mass 函数进行修正：

综合以上分析，本文采用证据权将专家Pk对属性集关于方案集的Mass 函数进行修正：

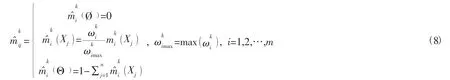
根据证据合成规则，将修正后的专家针对属性集关于方案集的Mass 函数进行合成，得到专家关于方案集的Mass 函数向量Mk。

3 实例分析

本文引用的实例来自于文献[5]，黑龙江省鸡西某煤矿于某日早晨井下发生爆炸，巷道烟雾较大，多处风井防爆门被摧毁，有黑烟冒出。经查四采区发生瓦斯爆炸，波及四采区下山至回风井所有区域，主要涉及325、326 两个回采工作面系统和437掘进工作面系统，井下共有211 名矿工，事故发生后，该矿立即启用应急救援响应机制，根据实际情况初步制定了4 项应急救援方案 xj（j= 1， 2，3，4 ），为最大限度保障井下被困人员安全和降低经济损失，现聘请3 位专家pk（k=1，2，3 ）根据下面6 项属性指标对救援方案进行评估，o1：灾区侦查和处理方法，o2：井下被困人员搜索方法，o3：恢复通风方法，o4：封闭及防止二次爆炸方法，o5：救灾人员的安全性，o6：救灾设备和资源搭配的合理性。给出专家权重分别为：0.32，0.35，0.33。

Step1：3 位专家给出每个方案关于属性集的直觉模糊评价值分别为：

Step2：根据记分函数定义，计算专家P1的记分函数矩阵L1：

Step4：根据式（3），计算专家P1对属性关于方案集的Mass 函数矩阵M1：

Step5：根据式（5） 和式（6），计算专家P1的属性权重向量：

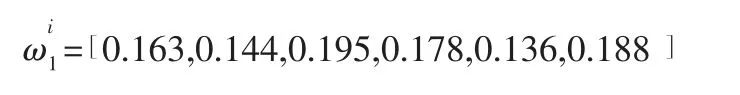
Step6：根据式（8），对M1进行修正，修正后进行证据组合，得到专家P1关于方案集的Mass 函数向量：

重复以上步骤分别得到3 位专家关于方案集的Mass 函数向量组合起来得到专家集关于方案集的Mass 函数矩阵M：

Step7：结合专家权重，再根据Dempster 组合规则进行合成得到三位专家关于方案集的Mass 函数向量M：

Step8：得出最终方案排序 x2＞x1＞x4＞x3。

4 结 论

在煤矿发生突发事故时，环境地质复杂，众多决策因素具有不确定性，结合证据理论与直觉模糊集能够很好地处理指标不确定及专家不精确偏好问题。本文实例分析的结果与引用文献的结果相一致，验证了该方法的有效性及可行性。整个决策方法体系简单，计算易于编程求解。不仅可应用于煤矿应急救援，还可以推广至其他应急决策领域。