整体架构下的动态生成

潘永斌

[摘  要] 文章对“微专题”教学的意义、如何科学合理设置“微专题”、如何进行有效的“微专题”课堂教学进行了阐述，介绍了如何在全局观下整体把握”微专题”，在实施教学过程中如何基于学情，动态生成“后微专题”及时补位，帮助学生跨越微专题学习的最后一道门槛进行了示范.

[关键词] 微专题;后微专题;整体架构;动态生成

对于高三数学一轮复习课，各地区基本都已给出了比较统一成熟且高效的课型模式，并成功实践多年，达成了共识，效果显著. 对于二轮复习的课型模式，可谓是“百花齐放”. 但多地区与学校现较多地采用“微专题”的形式，即针对某一具体知识点、问题，从其涉及的基本概念、基本原理、基本规律入手，精选例题和习题，探求知识方法和本源，领会解题思路和方法，固化解题模式和流程，它是一种“小切口”式教学的方法.

我国著名的数学教育家徐利治先生曾说过：“数学是模式的科学.”模式的概念更为深刻地揭示了数学的本质. 因此，“无论是数学中的概念和命题或是问题和方法，事实上都应被看成一种具有普遍意义的模式”. 解题的本质就是转化与化归，其遵循的熟悉化、简单化、直观化原则的核心是围绕模式识别来实施的. 如何让学生识别出模型，并熟练运用模式对其进行解决，这就需要通过系统、合适的微专题进行教学.

微专题教学“因微而准、因微而深、因微而活”，有利于促进学生对数学问题本质的理解. 因此，微专题教学已经成为很多地区、很多学校高三二轮复习的常态课堂教学形式.

与一轮复习不同，二轮复习“微专题”的设计编写与各地区、各学校学生的基础、能力及各地区不同的高考要求与侧重点等关系密切，可以说没有一种二轮“微专题”是放之四海而皆准的.这就要求教师要依据不同的学情、生情，在对二轮复习内容的整体把握下，动态生成适合自己学生的“微专题”.

下面笔者就以“导函数隐零点问题的探讨”为例来谈一谈对微专题设计的一些粗浅的想法.

全局观下的整体把握

“微专题”的微体现在其“切口小、研究深”上. 因此，对于微专题的设计，大部分教师是能够考虑到“小切口”这一要求的，即围绕某一个知识点或者是多个章节中存在的某一类具有共同特点的問题开展微型复习专题研究.

但在做到“微”之前，教师首先要对学生学习的“痛点”和高考命题的“热点”有全面而整体的把握，在全局观下用居高临下的视角全面审视高中数学的知识体系、逻辑结构和思想方法，通过一个由“宏”致“微”的过程，进而着眼于“痛点”，聚焦于“热点”，将点连成线、线形成面. 以“微专题”为载体，逻辑串联起高中数学的知识脉络和思想方法，注重系统性，整体谋划，布局合理.

基于如上考虑，确定“微专题”系列的内容便是首要完成的工作，在本文中笔者不加赘述. 下面笔者就谈谈对函数与导数内容，微专题的设计与实践.

笔者首先将2013-2019年江苏高考最后的压轴函数与导数问题整理如下（见表1）.

由此可见，函数与导数中的“隐零点”问题历来是一个命题“热点”和学生学习“痛点”，而“热点”与“痛点”的交汇处，既是失分的“死亡沼泽”，也可以是增分的“希望原野”，需要我们重点关注.

整体把握中的动态生成

（一）微专题设计与教学的一般模式

为了解决这一问题，我们设计了微专题《导函数零点难求问题的探讨》，通过对此问题的解决，能更好地促进学生深度学习，把握问题本质，解决核心难点，发展思维能力.

对于分解出的“微专题”，我们要让学生总结出其一般的解决模式，建构解决这类问题的规范方法与流程体系.因此，例题选择需全不需深，教师讲解时也宜简化前期的“准备工作”，如：该问题是如何转化与化归至此问题、对目标函数的求导、通分与因式分解等，将重点放在导函数的零点无法求得之后的各类情况分析与解决方式选择.通过对具体的各类问题的分析，学生再总结出解决这一类问题的模式与规范流程也就水到渠成了.

设计意图：通过零点存在性定理，可知导函数是有零点的，但是无法求解也无法观察出零点，可以通过假设零点，整体代换来解决此问题.

以上三个例题，基本涵盖了高考命题中零点无法求得的三种情况，即：（1）无零点;（2）可猜出零点，并可证明其唯一性;（3）有零点，但无法猜出，可假设零点，通过零点存在性定理限定其大概范围并对其进行整体代换.

通过以上三个典型例题的分析，学生可将导函数零点难求问题的常见情况与一般处理方法总结如下：

（二）基于学情动态生成“后微专题”

通过如上微专题的研究，学生在解题方法和解题思路上有了很大提升，面对一个新的问题普遍知道如何进行思考了，但在实际解题过程中依旧困难重重，难以将解题进行到底.究其原因，不同层次的学生既有共性的问题，也有个性的问题，概括起来主要有三个：一是有些问题参变量分离困难或不具备可操作性（参数分离需要解二次方程或不等式，需要用到“洛必达”法则，零点问题容易被扣分等），这些问题用整体法考虑对参数范围如何进行分类讨论仍有困难;二是如何利用零点存在定理判定零点存在;三是如何虚设零点、整体代换.毫无疑问，上述三个问题是学生学习的“痛点”，而且是“痛中之痛”.

对此，笔者又设计了三个“后微专题”，分别是《求导中含参讨论的二次型问题》《隐零点问题中零点存在性判断问题》《虚设代换与强化命题，破解导数的隐零点问题》.

1. 求导中含参讨论的二次型问题

例1：已知函数f（x）=ax2-（2a+1）x+lnx，试讨论函数f（x）的单调性.

设计意图：求导后舍弃恒正恒负部分后得到的代数式，可利用因式分解的办法来解决.

例2：已知函数f（x）=2lnx+ax2-4ax+3a，若对任意x∈（1，+∞），都有f（x）>0成立，求实数a的取值范围.

设计意图：求导后舍弃恒正恒负部分后得到的代数式，不能因式分解，但可以通过判断Δ，然后利用分类讨论来解决.

例3：已知函数f（x）=ax3-3x+1，若对任意的x∈[-1，1]，f（x）≥0恒成立，求实数a的值.

设计意图：求导后舍弃恒正恒负部分，然后利用参变量分离或者整体分类讨论来解决. 但如果能利用端点带入缩小参数范围，就能减少不必要的讨论，简化解题过程.

例4：已知函数f（x）=ax3+x2-ax（a∈R，且a≠0），如果存在实数a∈（-∞，-1]，使函数g（x）=f（x）+f ′（x），x∈[-1，b]（b>-1）在x=-1处取得最小值，求实数b的最大值.

设计意图：利用整体法来解决该问题需要分情况讨论，比较烦琐，如果能把问题转化为g（x）≥g（-1）恒成立，则可大大简化解题过程.

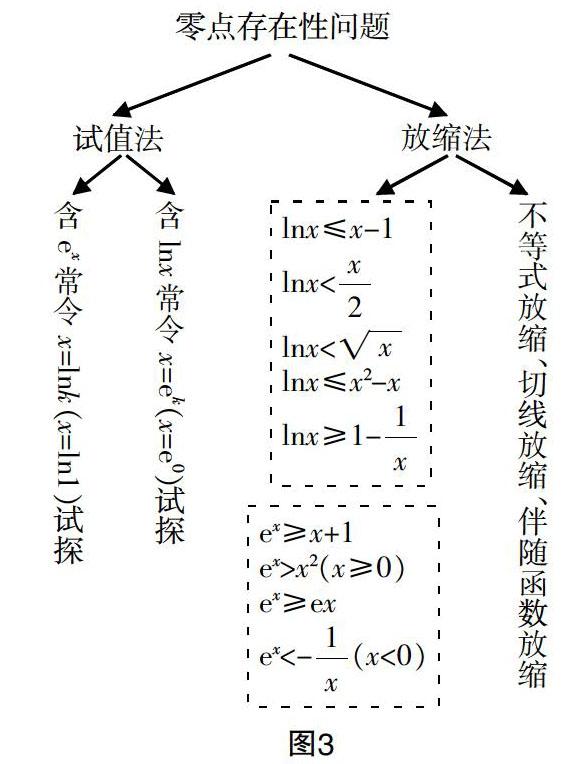
2. 隐零点问题中零点存在性问题

例1：若函数f（x）=lnx-x-a有两个不同的零点，求实数a的取值范围.

设计意图：一边用ea试值，另一边lnx≤x-1放过大，尝试lnx<或lnx<，从系数或次数上调整.

例2：设函数f（x）=lnx-ax有两个零点，求实数a的取值范围.

设计意图：不能用参变量分离，即使使用也会出现极限问题（型，洛必达法则）. 需采用整体法（一边用e0试值，另一边lnx≤x-1不满足，尝试lnx<）.

例3：已知函数f（x）=ex-2lnx++b

既有极大值，又有极小值，求实数b的取值范围.

设计意图：求导后通过舍弃恒正或恒负部分，经过换元转化为h（t）=lnt-2t+b有两个零点问题，体现了转化与化归的思想.

方法总结如下：

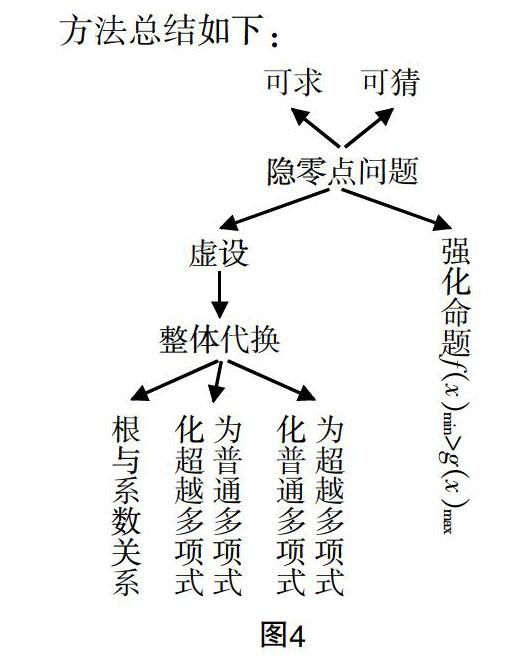
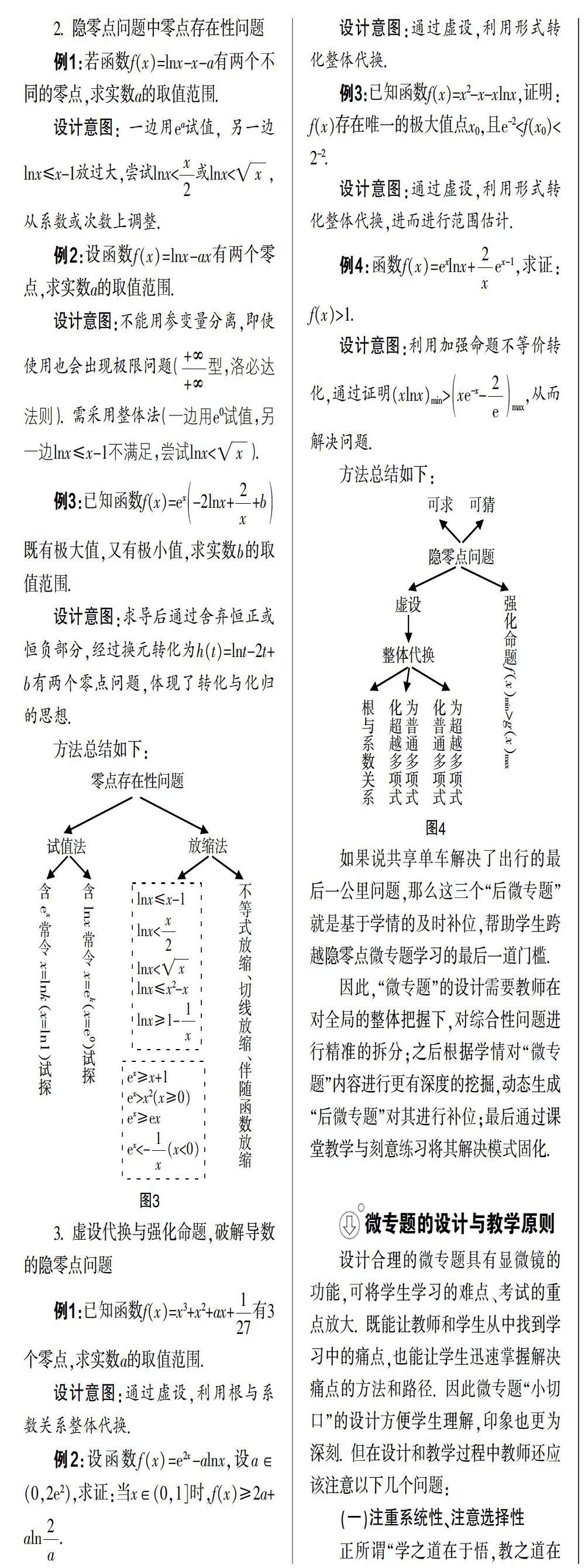
3. 虚设代换与强化命题，破解导数的隐零点问题

例1：已知函数f（x）=x3+x2+ax+有3个零点，求实数a的取值范围.

设计意图：通过虚设，利用根与系数关系整体代换.

例2：设函数f（x）=e2x-alnx，设a∈（0，2e2），求证：当x∈（0，1]时，f（x）≥2a+aln.

设计意图：通过虚设，利用形式转化整体代换.

例3：已知函数f（x）=x2-x-xlnx，证明：f（x）存在唯一的极大值点x0，且e-2

设计意图：通过虚设，利用形式转化整体代换，进而进行范围估计.

例4：函数f（x）=exlnx+ex-1，求证：f（x）>1.

设计意图：利用加强命题不等价转化，通过证明（xlnx）min>xe-x-max，从而解决问题.

如果说共享单车解决了出行的最后一公里问题，那么这三个“后微专题”就是基于学情的及时补位，帮助学生跨越隐零点微专题学习的最后一道门槛.

因此，“微专题”的设计需要教师在对全局的整体把握下，对综合性问题进行精准的拆分;之后根据学情对“微专题”内容进行更有深度的挖掘，动态生成“后微专题”对其进行补位;最后通过课堂教学与刻意练习将其解决模式固化.

微专题的设计与教学原则

设计合理的微专题具有显微镜的功能，可将学生学习的难点、考试的重点放大. 既能让教师和学生从中找到学习中的痛点，也能让学生迅速掌握解决痛点的方法和路径. 因此微专题“小切口”的设计方便学生理解，印象也更为深刻. 但在设计和教学过程中教师还应该注意以下几个问题：

（一）注重系统性、注意选择性

正所谓“学之道在于悟，教之道在于度”，微专题的例题选择宜低起点，主题明确，难度依次递进.不能因为是二轮复习，就拔高起点，我们应正确理解微专题教学中例题的功能：为寻求问题本质、探求思路方法、厘清一般解题流程服务. 在微专题复习中教师要引导学生对问题的本质、方法的本质深入探究，对不同问题不同方法加以辨析与比较，探求解决问题的一般流程，对解决问题的一般流程进行固化和训练，只有这样学生方能领悟方法的内涵并加以灵活运用.

（二）体现学生的主体地位

在微专题教学中，教师应突出学生交流活动的开展，体现学生的主体地位，引领学生进行思维碰撞、深度思考. 对微专题设计要进行更深层次的数学思考，善于变“习题”为“问题”，变“问题”为“课题”，变“讲授”为“悟道”，创设阶梯性问题链，让学生的学习具有挑战性，使学生通过自己的思考、探究、交流，悟出自己的数学学习之道.

（三）固化模式、反馈矫正、螺旋上升

在微专题的课堂教学之后，还需要教师对学生的掌握情况进行反馈矫正以达到预期效果.对于二轮复习，我们可以以微专题为载体，通过整体把握、选择问题;精准拆分、分解模块;深度挖掘、动态生成;模式固化、建构规范;反馈矫正、螺旋上升这一系列的工作使学生领悟题型和方法的内涵并习得自然.

当然，对学生单一动作的训练完成之后，我们还需要对其进行“实战训练”，即综合问题训练，从转化与化归开始，要求学生书写要清晰，表达要规范，计算要准确，颗粒归仓，循环往复，螺旋上升.

总而言之，微專题的编写目标——让学生走出“舒适区”，走进“学习区”;微专题的编写原则——微而不轻，难度适当;微专题的呈现形式——删繁就简，直击要害;微专题的规划方案——整体布局，动态生成;微专题的落实方式——模式固化，刻意练习. 唯有如此，才能更有效解决学生学习的“痛点”和命题的“热点”;唯有如此，学生的能力才能日益精进！