“椭圆及其标准方程”：从历史中寻找 “火热的思考”

马艳荣 叶佳浩 沈中宇

摘要：基于学生在学习中遇到的困难，考虑到数学史的教育价值，从HPM的视角设计“椭圆及其标准方程”的教学。椭圆及其标准方程的发展经历了漫长的过程，可以大致地分为五个阶段：椭圆概念（截线定义）的诞生，椭圆焦半径性质的发现，椭圆作图法的出现，椭圆第一定义（轨迹定义）的诞生，椭圆标准方程的推导。相应地，教学可以分为“生活引入，历史回顾”“性质探索，认识椭圆”“画图操作，定义椭圆”“方程推导，求解椭圆”“思想深化，玩转椭圆”等环节。课后反馈表明，这样的教学取得了较好的效果。

关键词：HPM椭圆及其标准方程重构式

沪教版高中数学教材在第12章《圆锥曲线》第三节《椭圆的标准方程》（前两节分别是《曲线和方程》《圆的方程》）中，通过圆柱形水杯倾斜时水面的边界线、玻璃窗上的圆投射到地面上的影子等生活实例让学生认识椭圆，然后借助“两钉一绳”让学生画出椭圆，进而直接给出椭圆的第一定义，后面利用“二次平方法”得到椭圆的标准方程。在实际教学中，学生常常会产生一些困惑：为什么这样的曲线叫作“圆锥曲线”？生活中的椭圆是否与“两钉一绳”画出的椭圆一致？椭圆方程的推导除了教材中的方法之外，还有没有更简便的方法？

基于学生在学习中遇到的困难，许多教师对这一内容的教学进行了探索。有教师选取一条没有弹性的细绳，让学生画出椭圆，然后得到椭圆的定义并推导椭圆的标准方程。有教师让学生探究圆是怎么压缩成椭圆的，然后经过逐步探究得到椭圆的画法，最后获得椭圆的定义。有教师借助折纸，让学生观察得到交点的轨迹，从而引出椭圆，然后探究椭圆的定义与标准方程。有教师带领学生经历从截线定义到轨迹定义（第一定义）的知识发生过程，基于旦德林双球实验，开展数学实验探究等一系列活动。

研究表明，学生头脑中存在两种椭圆的意象，分别是生活中的截线定义以及教材中的轨迹定义;学生对椭圆最初的认知是生活中的椭圆。历史表明，人们对椭圆最早的认知也来源于圆锥的截线。因此，在“椭圆及其标准方程”的教学中融入数学史符合学生的认知规律。同时，历史上椭圆方程的推导方法经历了不同的传承，除了教材中的“二次平方法”之外，还有很多精彩的方法，可以用它们来丰富我们的课堂。此外，融入数学史也有助于学生经历椭圆的发生、发展过程，体会数学背后的人文价值，培养动态的数学观，激发学习兴趣，发展数学素养，落实学科育人。

鉴于此，笔者从HPM的视角设计本节课的教学，拟定如下教学目标：（1）通过历史的回溯和几何画板的演示，掌握椭圆的概念以及标准方程;（2）经历从情境中抽象椭圆性质以及用数量关系形式重塑椭圆定义的过程，根据椭圆的定义建立椭圆的标准方程，进一步巩固求曲线方程的一般方法和步骤，体验用代数方法研究几何问题的思想，并体会多种推导方法，开阔视野;（3）经历椭圆定义的发展历程，感受其中蕴含的数学文化，体会数学家坚持不懈的探究精神。

一、历史材料梳理

椭圆及其标准方程的发展经历了漫长的过程，可以大致地分为五个阶段：

（一）椭圆概念（截线定义）的诞生

希腊哲學家普罗克鲁斯（Proclus，公元5世纪）告诉我们，柏拉图学派的梅内克缪斯（Menaechmus，公元前4世纪）是圆锥曲线的发现者，圆锥曲线一开始被称为“梅内克缪斯三线”（如图1）。后来，数学家亚里士塔欧（Aristaeus，公元前4世纪）将这三种曲线分别称为锐角圆锥曲线、

直角圆锥曲线和钝角圆锥曲线，分别对应于今天的椭圆、抛物线和双曲线。

亚里士塔欧曾著《立体轨迹》一书，对圆锥曲线做了进一步的研究。之后，欧几里得（Euclid，公元前3世纪）又著《圆锥曲线》一书，对圆锥曲线的研究成果做了系统性的总结。可惜，这两本书均已失传。

（二）椭圆焦半径性质的发现

在欧几里得《圆锥曲线》的基础上，阿波罗尼斯（Apollonius，公元前3世纪）撰写了一部划时代的巨著——《圆锥曲线论》。书中，作者将同一圆锥（并不局限于前人的正圆锥，而是更一般的斜圆锥，如图2）被不同位置的平面所截得的曲线定义为圆锥曲线。

阿波罗尼斯还从图2中，利用三角形的相似得到了椭圆的基本性质：PQ2AQ·QB=DQ·QEAQ·QB=MF·NFSF2=常数——实际上，等于短轴与长轴的平方比，也等于通径与长轴的比。之后，阿波罗尼斯又花了很大的力气得到了椭圆的焦半径性质：椭圆焦半径之和是定值。

（三）椭圆作图法的出现

以设计圣索菲亚大教堂而闻名世界的拜占庭数学家安提缪斯（Anthemius，约474—534）在研究燃烧镜时，给出了今天我们非常熟悉的椭圆的“两钉一绳”画法（如下页图3，今又称“园艺师画法”）。这一画法的依据就是阿波罗尼斯所发现的椭圆焦半径性质。

（四）椭圆第一定义（轨迹定义）的诞生

法国数学家和天文学家拉希尔（P.de Lahire，1640—1719）在《圆锥曲线新基础》一书（1679）

中给出了椭圆的焦半径定义，即椭圆的第一定义——平面上到两定点距离之和等于常数的动点轨迹。

法国数学家洛必达（M.de LHospital，1661—1704）在《圆锥曲线分析》一书（1707）中采用了“园艺师画法”以及拉希尔的椭圆第一定义，并根据该定义成功地推导出了椭圆的方程。

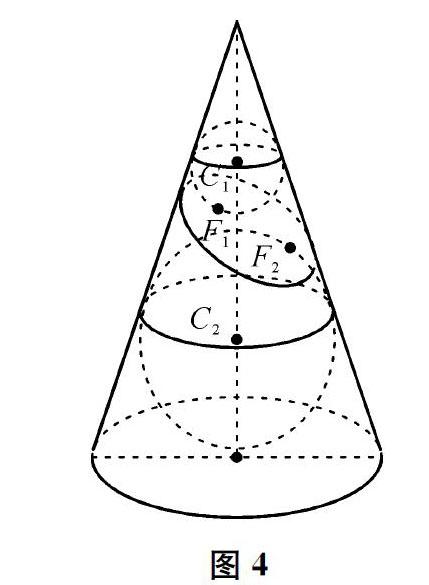
直到1822年，比利时数学家旦德林（G.P.Dandelin，1794—1847）才在一篇论文中利用圆锥的两个内切球（如图4），直接在圆锥上推导出了椭圆的焦半径性质，从而直观地证明了椭圆的截线定义与轨迹定义的统一性。

（五）椭圆标准方程的推导

洛必达在《圆锥曲线分析》中采用以下方法推导椭圆的方程：

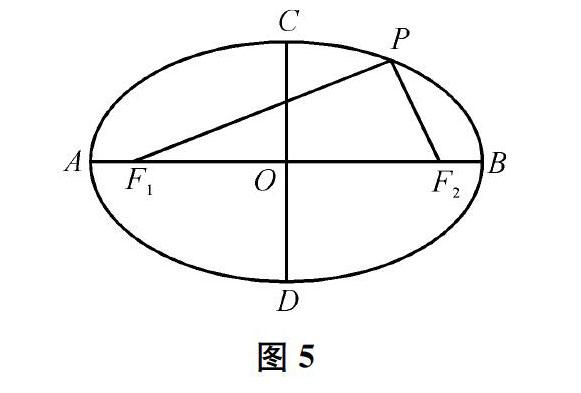
如图5所示，设长轴AB=2a，短轴CD=2b，焦距F1F2=2c，P（x，y）是椭圆上的任意一点。因为PF1+PF2=2a，可设PF1=a+z，PF2=a-z，其中z为待定参数。利用两点之间的距离公式，得出PF21=（a+z）2=（x+c）2+y2，PF22=（a-z）2=（x-c）2+y2。两式相减，得4az=4cx，即z=cxa。将其代入前式，得a2+2cx+c2x2a2=x2+2cx+c2+y2。于是可得椭圆方程y2=b2a2（a2-x2）（其中令a2-c2=b2）。

洛必达设PF1、PF2的方法被称为“和差术”，起源于古代两河流域，并被希腊数学家丢番图（Diophantus，约200—284）在《算术》一书中频繁使用于二次方程的求解。洛必达称他得到的方程用长、短轴之比完美展现了椭圆的性质，但他并未将其化为今天的标准形式。

1836年，英国数学家赖特（J.M.F.Wright）在《圆锥曲线之代数体系》一书中采用“平方差法”（源于分子有理化思想）推导出椭圆的标准方程：

如图5所示，设PF1=r1，PF2=r2，则r21=（x+c）2+y2，r22=（x-c）2+y2。两式相减，得r21-r22=4cx，即（r1+r2）（r1-r2）=4cx。又由r1+r2=2a，可得r1-r2=2cxa，进而可得r1=a+cxa，r2=a-cxax。将其代入前式，整理得方程x2a2+y2b2=1（其中令a2-c2=b2）。

在19世纪的教科书中，基于第一定义的椭圆方程推导方法百花齐放。然而，到了20世纪，大多数教科书采用了椭圆的第二定义，而采用第一定义的教科书在推导椭圆方程时几乎都选择了“二次平方法”。

二、教学设计与实施

根据上述历史阶段的划分，本节课的教学可以分为以下几个环节：

（一）生活引入，历史回顾

师（出示下页图6）将装有水的圆柱形水杯倾斜放置，此时水面所形成的形状是——

生 椭圆。

师小球被平行光倾斜照射所形成的影子的轮廓，圆柱（锥）形建筑被平面斜截所得的截口，这些又是什么形状？

生 椭圆。

师为什么说这些形状是椭圆？到底什么是椭圆？椭圆为何安排在《圆锥曲线》这一章中？带着这些问题，一起来看一段视频。

（播放视频，回溯椭圆及其方程的发生和发展历程：古希腊人与削尖的圆木桩—平面斜截不同圆锥产生圆锥曲线—圆锥曲线的进一步研究与总结—“园艺师画法”—阿波罗尼斯与椭圆的焦半径性质—平面截同一圆锥的不同位置定义圆锥曲线—拉希尔与椭圆的第一定义—笛卡儿和费马创立解析几何—洛必达成功推导椭圆的方程。）

（二）性质探索，认识椭圆

师大家看完视频，可能会存在疑惑，到底椭圆的截线定义与第一定义有什么联系？接下来，我们将借助旦德林双球模型架起古希腊时期与17世纪椭圆定义的桥梁。（稍停）为此，我们先设置两个关卡来引导大家理解。在平面上，过圆外一点引圆的切线，有几条？切线长之间有什么关系？

生两条，相等。

师 （出示图7）类比到空间中，过球外一点引球的切线，有几条？这些切点会形成什么图形？这些切线长之间有什么关系？

生 切线有无数条，切点会形成圆，切线长都相等。

师 大家顺利通过第一关，现在来到第二关。将一个半径等于圆柱底面圓半径的小球放入圆柱，则小球和圆柱的位置关系如何？

生 相切。

师 切点有几个？会形成什么图形？

生 切点有无数个，会形成圆。

师 那不妨记这个圆为C1。现在将另一个同样大的小球也放入圆柱，则它和圆柱也相切，切点也有无数个，也会形成圆。我们将这个圆记为C2。那么，C1和C2所在平面的位置关系如何？

生 平行。

师 很不错！设圆柱的一条母线交圆C1于点P，交圆C2于点Q，那么PQ与这两个平面是什么关系？与两个小球的位置关系又如何？

生 与两个平面垂直，与两个小球相切。

师 现在将母线动起来，在运动的过程中，PQ的长度变不变？

生 不变。

师很好！大家顺利过关，现在已经完全具备了基础知识。下面让我们一起来揭开旦德林双球模型的神秘面纱吧！（出示图8）首先，用一个平面斜截圆柱，所得交线即为椭圆，这也是古希腊时期椭圆的由来。然后，从圆柱上方放入一个小球，使得这个小球与椭圆面相切，那么有几个切点？

生 一个。

师 很好！不妨将该切点记为F1。在椭圆上任取一点M，那么MF1与这个小球的位置关系如何？

生 相切。

师接着，从圆柱下方放入另一个同样大的小球，使得这个小球也与椭圆面相切，那么也有一个切点。不妨将该切点记为F2，那么MF2与这个小球相切。如果过点M作刚才的PQ，思考一下：会得到哪些结论呢？

（学生思考。）

生 MF1与上方小球相切，MP也与上方小球相切，所以，MF1与MP相等。

师没错！通过刚才的铺垫，我们知道过球外一点引球的切线，切线长相等。同样，MF2、MQ和下方小球相切，所以，MF2=MQ。那么，在点M运动的过程中，图中哪些量不变？椭圆上的点M又会满足什么关系？

生 PQ长度不变。

生 MF1+MF2=MP+MQ=PQ。

师 我们知道，圆上任意一点到一个定点的距离等于定长，你能类比得出椭圆上任意一点所满足的性质吗？

生 椭圆上任意一点到两个定点的距离之和为定值。

师 非常好！

（三）画图操作，定义椭圆

师我们刚才得到了一个性质，椭圆上的点都满足这一性质。反之，根据这个性质得到的点的轨迹一定是椭圆吗？能否将这一性质作为椭圆的定义呢？如果不行，需要增加什么限制条件？带着这个问题，一边画图，一边思考。同桌两人配合，利用细绳尝试画一个椭圆，画的时候思考一下如何体现定点和定长。

生 一个人钉住绳头，另一个人画。绳头就是定点，绳长就是定长。

师 好！大家动手操作一下。同时，请一个同学利用椭圆规在黑板上画一下。

（学生画图。）

师 其实，大家刚刚体验的就是“园艺师画法”。回到我们的问题，要增加什么条件，才一定能画出椭圆呢？

生 绳长一定要大于绳头之间的距离。

师 绳头就是两个定点;绳长就是椭圆上任意一点到两个定点的距离之和，是个常数，记作2a。也就是说，在椭圆上任取一点M，则M、F1、F2构成三角形，或M在F1F2的延长线上，即MF1+MF2（=2a）>F1F2。那么，若2a=F1F2，得到的点的轨迹如何？若2a

生 2a=F1F2时，轨迹是一条线段。2a

师 不错！那么，现在这个椭圆定义是否完整呢？

生 应该是平面上到两个定点F1、F2距离之和为常数2a的点的轨迹是椭圆，且2a>F1F2。

师 大家给自己一点掌声！你们通过上述从模型到作图的过程，自行给出了和书本上一致的椭圆定义。其中，定点F1、F2称为焦点，焦点F1、F2之间的距离F1F2称为焦距，用2c来表示。这就是完整的椭圆定义。

（四）方程推导，求解椭圆

师 知道了椭圆的定义，下面就开始求椭圆的方程。求曲线方程的基本步骤是什么？

生 建系，设点，列式，化简，检验。

师 很好！那如何建系？

生 以F1F2为x轴、F1F2的垂直平分线为y轴，建立直角坐标系。

师 嗯，不错！这样可以充分利用椭圆的轴对称性。老师觉得，这样建系求出来的方程会比较简洁。根据对称性，除了将F1、F2放在x轴上，还可以把F1、F2放在y轴上。就先以F1F2为x轴、F1F2的垂直平分线为y轴，建立直角坐标系。根据F1F2=2c，你能给出F1、F2的坐标吗？

生 F1（-c，0）、F2（c，0）。

师 接下来，设点，列式。设M（x，y），根据MF1+MF2=2a，这两个距离如何用坐标表示？

生 利用两点之间的距离公式。

师 至此，我们已经列好式了。下面有一个关键的问题：如何化简？

生 先移项再平方。

师 不错！平方去掉根号是最直接的想法。就请大家动手操作一下。

师 我们从之前得到的性质（也就是定义）出发，一步步推出了最后的方程。那得到的这个方程能叫作椭圆的方程吗？

生 不能，没有反过来验证。

师 很好，大家都非常严谨！知道了椭圆上的点的坐标都满足这个方程，还要反过来说明以这个方程的解为坐标的点都在椭圆上，满足椭圆的性质（也就是定义）。大家课后思考一下，下节课处理。（出示图9）现在观察这幅图，你能从中找出表示a、c、a2-c2的线段吗？

师实际上，还有OA=OB=a。可见，他们都有明显的几何意义。不妨令a2-c2=b，得到x2a2+y2b2=1，这就是焦点在x轴上的椭圆标准方程。写成这一形式，体现了数学中求简、求美的思想。显然，a>c>0。那么，a、b满足什么数量关系？

生 a>b>0。

（五） 思想深化，玩转椭圆

师下面我们继续来玩转（x+c）2+y2+（x-c）2+y2=2a。刚刚我们通过“平方再平方”的方法得到了椭圆的标准方程，虽然思考上比较自然，但是计算量太大。还有其他更好的处理根号的方法吗？

生 分子有理化。

师 分子有理化的第一步怎么做？试试看。

师掌声献给她！之所以想到分子有理化，是因为平方差非常好算，结果也简单。

生刚刚这种方法也体现了换元思想：通过换元找r1、r2的关系式，然后解r1和r2，使过程的表达非常简洁。

师说得很好！既然提到了换元，老师再给大家介绍一种非常神奇的方法。对于等差数列{a，b，c}，即a+c=2b而言，我们知道b加上公差就是c，b减去公差就是a。所以，可以令（x+c）2+y2=a+t，（x-c）2+y2=a-t。这种处理方式在很多不等式的证明中都会用到。既然引入了一个参数，那么该如何处理这个参数呢？

生 消参。

师 说消参也对。我们应该找到这个参数，就是要用已知的a、c来表示t。如何表示？

师说得太棒啦！其实，代回去得到的就是椭圆的焦半径公式，这样就很容易推导出椭圆的方程。这两种“平方差法”在历史上都出现过。前一种是由19世纪英国数学家赖特发现的，后来被收录到俄罗斯的课本中。后一种被法国数学家洛必达采用过，其中的换元方式十分巧妙，被称为“和差术”，从古代两河流域就开始存在，后来希腊数学家丢番图也将其用于解方程。同学们今天通过不断地思考，也和伟大的数学家一样，感受到了数学的魅力。

（六）课堂小结，欣赏椭圆

师本节课，在知识层面上，我们主要学习了椭圆的定义及其标准方程;在方法层面上，我们主要知道了处理根式的几种方法，即“和差术”以及“平方差法”;在思想层面上，我们学会了利用解析思想解决几何问题，类比平面问题解决空间問题。此外，在情感层面上，无论介绍历史的视频，还是旦德林双球模型，古代数学家向我们展现的智慧，相比于书本上通过“两钉一绳”作图直接给出的椭圆定义，更让我们受益匪浅。这些“冰冷的美丽”背后蕴含着“火热的思考”。希望我们能好好学习数学家的探索精神，在以后的学习中更上一层楼！

三、学生反馈

课后，我们收集了全班73名学生对本节课的反馈信息。

针对课堂的整体情况，98.6%的学生表示听懂了这节课的教学内容;85.0%的学生表示非常喜欢和赞成教师用融入数学史的方式来讲授“椭圆及其标准方程”;82.2%的学生认为这节课中讲数学史比讲解大量例题更有意义。此外，74.0%的学生希望教师在以后的数学课中也采用这种方式授课，78.1%的学生表示非常愿意了解数学概念发生、发展的历史。可见，大部分学生对数学史融入数学课堂持有积极的态度和深切的期许。

针对椭圆概念的理解情况，问卷借鉴高考题设置了以下问题：“AB是平面α的斜线段，A为斜足。若点P在平面α内运动，使△ABP的面积为定值，则动点P的轨迹是。请写下你的思考过程。”72.6%的学生能够给出正确答案“椭圆”，他们有的将其想象成斜截圆锥来思考，有的借助椭圆定义来推理，有的借助投影来获取，有的类比旦德林双球模型来探索。少部分学生由于不熟悉椭圆的性质和定义，给出答案“圆”“线段”或“平行直线”。

问卷设置了如下问题来检测学生的“椭圆”意象：“看到‘椭圆二字，你会想到什么？”58.9%的学生想到椭圆的标准方程及长轴、短轴和焦距、焦半径;42.3%的学生想到椭圆的定义及其发展史;54.8%的学生想到用解析几何思想建立直角坐标系，列方程进行代数处理;71.2%的学生想到生活中各种各样的椭圆形状;28.8%的学生想到“园艺师画法”。可见，通过本节课的学习，无论知识本身还是多元文化，抑或思想方法层面，大部分学生都有所收获。

问卷还设置了一个问题来了解学生这节课中印象最深的内容。典型的回答如下：“视频让我对圆锥曲线的发展、椭圆的定义有了更深的了解，开阔了我的视野。”“几何画板所呈现的旦德林双球模型，能帮助我更好地学习椭圆的性质，了解定义的由来。”“除了课本上的推导方法以外，历史上竟然还有这么多精彩巧妙的推导方法。”“通过自己的一步步思考、发现来学习新知识，更有参与感，充满成就感。”可见，学生对椭圆定义的发展史、旦德林双球模型的探索以及各种巧妙化简方程、处理根式的方法印象深刻，也进一步体会到“冰冷的美丽”背后的“火热的思考”。

四、教学反思

本节课应用数学史的方式主要有重构式和附加式。基于椭圆定义和椭圆方程的演变与发展，师生一问一答、交流碰撞，从认识椭圆、定义椭圆、求解椭圆到玩转椭圆，环环相扣、深入思考，重构了历史的过程。丰富的数学史素材为对话式课堂教学带来了有趣的话题，搭建了沟通的平台。同时，借助视频帮助学生认识椭圆，向学生附加展示了历史上数学家的贡献以及椭圆的发生、发展，让课堂生动活泼、趣味不断。

本节课体现了数学史多元的教育价值。借助旦德林双球模型架起古希腊时期与17世纪椭圆定义的桥梁，探索椭圆性质，重塑椭圆定义，巧妙推导椭圆方程，构建了“知识之谐”;不断地激发学生思考，让学生在画图的过程中体会椭圆的定义，在讨论的过程中化简椭圆的方程，展现和数学家一样的智慧，营造了“探究之乐”;推导椭圆的标准方程时，书本上的“二次平方法”计算复杂，历史上的“和差术”和“平方差法”简洁巧妙，拓宽了学生的思维，彰显了“方法之美”;思考模型形成过程中的变量与不变量，类比圆的定义抽象椭圆的定义，探索含有两个根式方程的化简思路，培养了学生数学抽象、直观想象、逻辑推理和数学运算等核心素养，实现了“能力之助”;数学史揭示了数学知识是不断演进的，而不是一成不变的，“冰冷的美丽”背后蕴含着“火热的思考”，展示了“文化之魅”;引导学生跨时空与古人对话，了解古人精彩的推导方法，激发学生的学习兴趣和自信，让学生体会数学背后的探索精神和人文元素，达成了“德育之效”。

参考文献：

[1] 邹佳晨.椭圆的历史与教学[D].上海：华东师范大学，2010.

[2] 齐艳.“椭圆及其标准方程”教学案例及反思[J].中学数学教学参考，2018（24）.

[3] 王跃辉.椭圆定义的探究性教学设计与教学建议[J].数学通报，2013（5）.

[4] 李莹.“椭圆的标准方程（一）”的教学思考[J].中小学数学（高中版），2018（4）.

[5] 陈峰，王芳.基于旦德林双球模型的椭圆定义教学[J].数学教学，2012（4）.

[6] 王芳，汪晓勤.HPM视角下椭圆概念教学的意义[J].中学数学月刊，2012（4）.

[7] 汪晓勤.椭圆第一定义是如何诞生的？[J].中学数学月刊，2017（6）.

[8] 汪晓勤.椭圆方程之旅[J].数学通报，2013（4）.

[9] 汪晓勤，王苗，邹佳晨.HPM视角下的数学教学设计：以椭圆为例[J].数学教育学报，2011（5）.

[10] Wang，X.，Qi，C.，Wang，K.A Categorization Model for Educational Values of the History of Mathematics[J].Science & Education，2017（7-9）.

[11] 吳文俊.世界著名科学家传记：数学家II[M].北京：科学出版社，1992.

[12] Heath，T.L.A History of Greek Mathematics[M].London：Oxford University Press，1921.

[13] Wright，J.M.F.An Algebraic System of Conic Sections & Other Curves[M].London：Black & Armstrong，1836.