寻根溯源，以文化促生长

刘娟

摘要：随着新课程改革的实施，数学教学的文化价值在课堂教学中显得越来越重要。但在平时教学中，我们更多地关注数学的知识性、应用性，忽视了数学本身所蕴含的鲜活的文化背景，这使得师生常常囿于“知识就是这样的”，即知识抽象后的结论形态，很少有人追溯“这个知识怎样成为这样的”，即数学知识产生的过程。因此，在教学中我们要把数学知识的生长恰到好处地扎根在数学文化的土壤里，那么学生对数学知识的学习就越扎实。

关键词：数学教学;寻根溯源;数学文化;生长

数学文化究竟是什么？《数学课程标准》中曾明确提出了数学是一种文化：“数学是人类的一种文化，它的内容、思想、方法和语言是现代文化的重要组成部分。”而普通高中数学课程标准（实验）解读中提到：“一般说来，数学文化表现为在数学的起源、发展、完善和应用的过程中体现出的对于人类发展具有重大影响的方面。它既包括对于人的观念、思想和思维方式的一种潜移默化的作用，对于人的思维的训练功能和发展人的创造性思维的功能，也包括在人类认识和发展数学的过程中体现出来的探索和进取的精神和所能达到的崇高境界等。”由此可见，数学文化对数学教育的影响。

数学上的每一个发现或发明，总是在一定的文化背景下的某一种思考。数学教学应当努力还原、再现这一发现或发明的过程，从数学家的废纸篓里寻找数学知识的源泉，尽力向学生展现数学知识的产生、发展的过程，使学生在追寻数学发展的历史足迹过程中，能够看到数学知识形成的过程和发展的趋势，也就能够触摸到数学知识的来龙去脉，使学生在学习的过程中真正得到数学文化的熏陶，让数学知识恰到好处地在数学文化的土壤里生长。现结合本人的教学实践学习浅谈几点关于数学教学中追溯数学知识原点的体会。

一、关注学生的疑问，追根溯源，帮助学生解惑

美国哈佛大学有句名言：教育的真正目的就是让人不断提出问题、思索问题。德国教育家第斯多惠曾指出：“一个坏的教师奉送真理，一个好的教师则教人发现真理。”那么教师已不再是传统的知识的灌输者，而应是一个促进学生有效建构意义的“协助者”，是细心呵护学生问题意识的培育者。因而，教师在教学时，要关注学生的疑问，即“知识为什么是这样的”，从而帮助学生理决心中的疑惑。

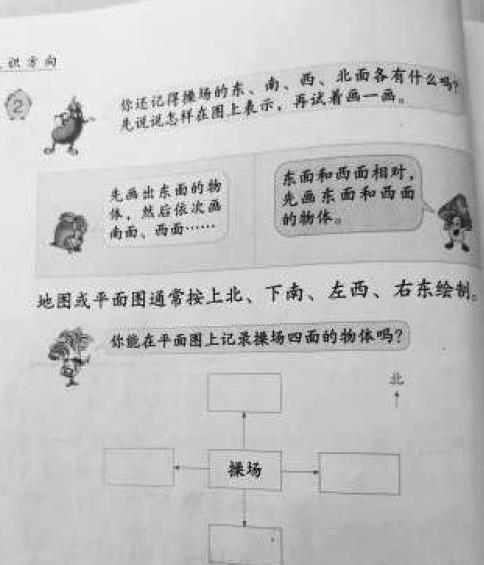
苏教版二年级下册的《认识简单的平面图》是在学生已经认识了东、南、西、北的基础上，把现实空间的方向转换到平面图上，需要较好的空间观念的支持。教学时，学生先联系第19页“想想做做”第4题的观察和记录，说说操场的东、南、西、北面各有什么，同时组织讨论：如果要用一幅图把操场四周的建筑物或场所表示出来，可以怎样做？由此要求学生按自己的想法试着图一画，然后通过对不同平面图的展示与比较，使学生体会到：由于标准不同，绘制的平面图也各不相同，这样不便于交流。进而认识到绘制平面图应有一个统一的标准。在此基础上，教师指出“地图或平面图通常按上北、下南、左西、右东绘制”。但这时课堂上有一位学生对此提出疑问，即“为什么地图上要按上北、下南、左西、右东来绘制，为什么不以其他来规定？”为帮学生解惑，使学生了解知识产生的根源，我向学生讲述其中缘由。一方面中国古代建筑都是习惯朝南建造，获得温暖采光。就连古代官殿都是座北朝南的，帝王的座位设在北方，面向南方。因帝王是一朝之长，万人之上，所以帝王坐在北边，北就为“上”。而坐在南边的群臣则为卑下，南就称为“下”了，后来又带进了人们的实际生活。比如看地图时，有一个共同的标准：即上北、下南、左西、右东。另一方面世界地图最早是由意大利传教士利玛窦介绍给徐光启的，叫做《坤舆万国全图》。当时《坤舆万国全图》就是上北下南，是当时的通用绘图方法。

在教学例2中，学生通过交流、画图、展示、比较等活动体会到：由于标准不同，绘制的平面图也各不相同，这样不便于交流。进而认识到绘制平面图应有一个统一的标准。但绘制平面图的统一标准是以教师“告诉”的方式呈现，学生对“为什么是这样的”的原因不太清楚。而恰好一位学生的疑问，问出了数学知识所蕴含的鲜活的文化根源，使学生更加深刻地明自“知识为什么是这样的”。

这样一种学习经历，使得数学在学生的眼里不再是死板的，相反，数学是一种鲜活的事物，它产生于人们的生活中，又服务于人们的生活。教师通过学生的疑问，合理有效地將数学文化渗人到实际的数学教学中，和学生一起找寻知识形成的根源，追溯数学知识的原点，使得数学知识的学习在数学文化的土壤里得到扎实的生长。

二、留住学生的意外追根溯源帮助学生建构

叶澜教授曾说过课堂教学“是一个动态生成的过程，再好的预设，也无法预知课堂教学中的全部细节。”教学中随时都有可能出现意外的通道和美丽的图景，问题在于，当“意外的通道”出现的时候，我们是否能够敏锐地意识到，并且能否经由这“通道”引领学生欣赏“美丽的图景”，帮助学生追溯思维的原点，从而达到建构。

《认识几分之一》是苏教版三年级上册第七单元的起始课，这一单元教材是在学生已经掌握一些整数知识的基础上进行教学的。这是学生第一次接触分数，从整数到分数是学生认识数的概念的扩展，是一次质的飞跃，因为无论在意义，读、写方法，还是在计数单位以及计算方法上，它们都有很大的差别，并且学生在生活经验中又接触得较少，接受起来比较困难。因此，一位特级老师在教学《认识几分之一》一课中，学生在表示“半个”时，出现1/2与2/1，为帮助学生正确书写分数理解其意义，特级教师向学生介绍分数产生的背景与过程。其实分数早就产生了，在古代，人们分东西（果实、猎物）时经常出现结果不是整数的情况，于是，渐渐产生了分数。在一开始，人们对分数也有各种各样的表达方式。在我国，很早就有了分数，最初用算筹表示，例如，把一个物体平均分成4份，每1份就表示成。古埃及人曾用象形符号表示分数，把《二）写在整数的上端，表明这是一个分数。例如：把一个物体平均分成4份，每1份就表示成这样琦开}。古巴比伦人用楔形文字表示分数，例如：把一个物体平均分成60份，其中的20份就表示成<乡。后来印度人发明了数字，用和我国相似的方法表示分数。例如：把一个物体平均分成4份，每1份就表示成1/4。不同地区不同的表示方法，你觉得他们如果相互交流起来会怎样？（相互不理解）。因此，为了交流、沟通起来更加方便，人们逐渐统一了分数的书写形式。随着印度人发明了数字，再往后，阿拉伯人发明了“一”，就把分数表示成现在这样了。例如：把一个蛋糕平均分成2份，每1份就表示成1/2，一般读成“二分之一”。注意看二分之一怎样写。（教师板书示范）

在教学中，先让学生用自己的方法尝试怎样表示每人分得多少，出现了1/2与2/1两种表示方法，到底哪一个是正确的书写方式，教师抓住这次的生成性资源，向学生介绍今大创造出来的数，即分数产生的背景与过程，使学生的学习不在囿于“分数就是这样的”，而是让学生真正了解分数是在哪里生长出来的，从而在整数的基础上构建对分数的认识。

这样一种学习经历，使得数学在学生的眼里不再是枯燥的，相反，数学是一种创造的启迪，它产生于人们已有的旧知，但又不够解决新的问题，于是，渐渐人们在原有的基础上创造。教师通过学生的意外，合理有效地将数学文化渗人到实际的数学教学中，和学生一起找寻知识形成的根源，追溯数学知识的原点，使得数学知识的学习在数学文化的土壤里得到扎实的生长。

三、抓住学生的难点追根溯源帮助学生理解

教学重点来自于知识本身，是由于数学知识内在的逻辑结构而客观存在的，因而对每一个学生均是一致的。教学难点却不同，它依赖于学生自身的理解和接受能力。实践证明不同层次的学生对于同一知识点的难点突破速度与水平是参差不齐的。因而，教师在教学时，要关注学生的难点，即“知识为什么是这样规定的”，从而帮助学生突破难点，使学生更好地理解数学知识。

苏教版三年级下册的《认识平年和闰年》主要是教学平年和闰年的初步认识，以及判断某个年份是平年还是闰年的基本方法。学生先观察2005-2016年2月的大数，通过比较及相应的交流，使学生认识到：2月可能有28天，也可能有29犬;在给出的年份中，2008年、2012年和2016年的2月都有29大，其余年份的2月则有28天。在此基础上，介绍平年和闰年的含义，并进一步指出判断平年和闰年的基本方法，但学生对“为什么每4年里通常有3个平年、1个闰年”的却不太清楚。除此之外，教材还通过底注补充说明判断整百年份是不是闰年的方法，但大部分学生不理解为什么遇到整百年份必须要除以400没有余数才是闰年，所以在练习中会出现把2100年判断为闰年的错误。因此，在这里针对学生的两个难点，联系“你知道吗”的数据，并通过必要的推算，帮助学生初步理解：因为地球绕着太阳不停地旋转，每转一周需要365大5时48分46秒。为了方便，人们把一年规定为365大。这样，每经过4年就多出23时15分零4秒，把这大约多出的1天加在2月里，这一年就有366天。因此，通常每4年里有3个平年、1个闰年。但由于把23时15分零4秒当作24小时，所以每4年多算了44分56秒。这样一来，每400年就多算了3大2时53分20秒。于是，每400年至少要减少3个闰年。于是，就有了“四年一闰，百年不闰，四百年又闰”的规定。

在教学中，学生通过观察、发现、交流、等活动体会到：每4年里通常有3个平年、1个闰年，但“为什么是这样的”学生不太清楚原因。此外，对于教材底注的内容如果不加以解释，学生只会停留在表象的记忆，而没有深层次的理解。这里教师联系“你知道吗”里的数据，并通过必要的推算，帮助学生初步理解，既拓宽了学生的知识视野，又有助于学生更加透彻地理解相关知识，体会数学方法的严谨性和确定性。

这样一种学习经历，使得数学在學生的眼里不再是深奥的，相反，数学是一个广阔的领域，它涉足地球、月球、航空航大等领域，使得学生对数学知识的理解有了深度和广度。教师通过学生的难点，合理有效地将数学文化渗人到实际的数学教学中，和学生一起找寻知识形成的根源，追溯数学知识的原点，使得数学知识的学习在数学文化的土壤里得到扎实的生长。

那么数学教学不单纯是数学科学的教学，更应该是数学文化的渗透。正如齐友民先生所说：“历史已经证明，而且将继续证明：一种没有相当发达的数学文化是注定要衰落的，一个不掌握数学作为一种文化的民族也是注定要衰落的。”因此，教师必须提高自身的数学文化素养，教学视野必须从“如何有效让学生接受知识是这样的”进而关注“如何发展让学生思考知识是怎样生长成这样的。”这样学生的数学知识的学习才能在数学文化的土壤里扎实的生长，而不是停留在学生表面的知识教学而已。

参考文献

[1]肖川.义务教育数学课程标准解读[M].湖北教育出版社，2011.

[2]孙丽谷，王林.义务教育教科书——数学[M].江苏凤凰教育出版社2015.

[3]马梅.浅谈在小学数学课堂教学中渗透数学文化[J].教育教学论坛，2013（37）：82-82.

[4]严士建，张奠宙，王尚志.普通高中数学课程标准（实验）解读[M].江苏教育出版社，2004.

[5]王兆正.生长性：数学知识教学的应然追求[J].江西教育，2011（Z3）：29-30.

[6]熊妍茜.数学文化在小学数学课堂教学中的实践探索[D].西南大学，2016.