GPS数字锁相环路设计及分析方法＊

石 岚

（陕西国防工业职业技术学院，陕西 西安 710300）

锁相环在通信、遥测、导航等领域有着广泛的应用,目前的工程应用以二阶环为主,三阶环由于其对加速度的跟踪能力,也得到一定程度的应用,并正受到越来越多的重视。跟踪GPS信号需要两个相互依赖的跟踪环:一个用于跟踪载波频率,称为载波跟踪环；另一个用于跟踪C/A码码相位,称为码跟踪环。这些锁定环虽然名称不同,但是都是属于锁相环的范畴。本文对这些环路的性能进行对比分析。

1 锁相环线性模型

基本锁相环主要用于调节本地晶体振荡器的输出频率来和输入信号的频率相匹配。基本的PLL如图1所示。

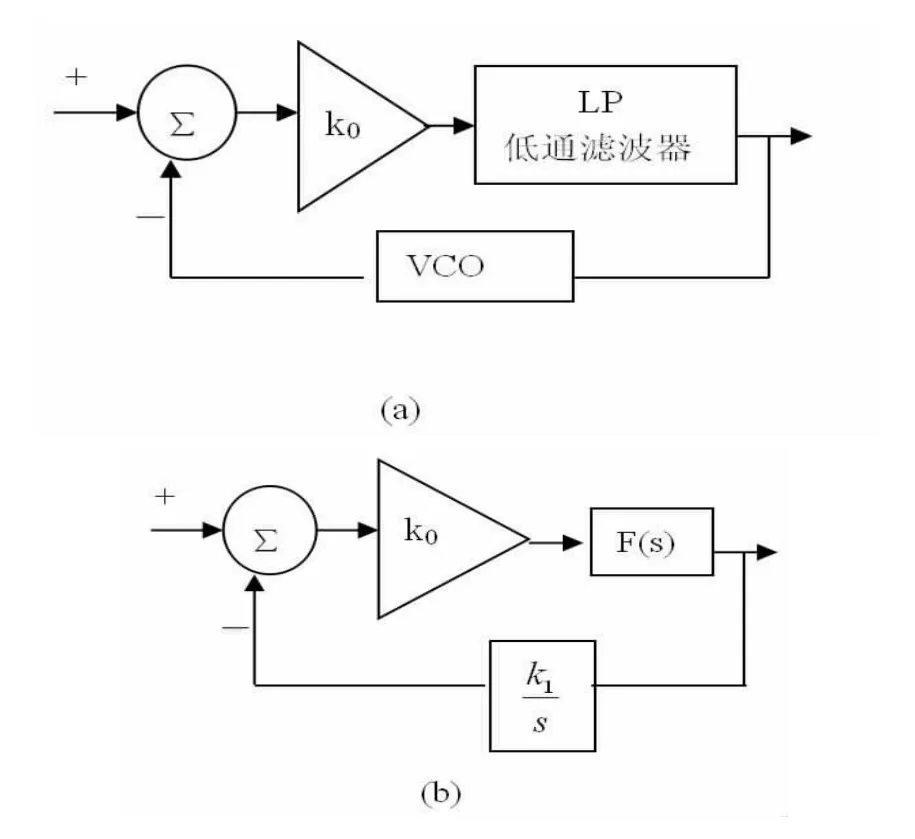
图1 基本锁相环

图1(a)是时域结构，图1(b)是经过拉普拉斯变换后的s域结构。

其开环传递函数为

闭环传递函数为

误差传递函数为

其中F(s)为锁相环低通滤波器传递函数,k0为放大器增益,k1为VCO的增益，由于是简单相乘关系，本文中统一为k=k0×k1。可以看出,环路低通滤波器的传递函数不仅可以决定PLL的阶数,自然频率,衰减系数,噪声带宽,还很大程度上影响PLL的性能,因此,环路低通滤波器是PLL的关键组成部分。

2 环路低通滤波器

环路低通滤波器的作用是降低噪声以便在滤波器输出端对原始信号产生精确的估计。环路低通滤波器的阶数和噪声带宽决定了低通滤波器对信号的动态响应。GPS系统中常用的1阶和2阶环路低通滤波器函数分别为：

图2给出了这两种环路低通滤波器的方框图[1]。

图2 环路低通滤波器

为了建立数字化处理的软件锁相环，必须将离散系统转变为数字系统，采用双线性变换法将传递函数连续的s域模型转变为数字的z域模型，转换方法为：

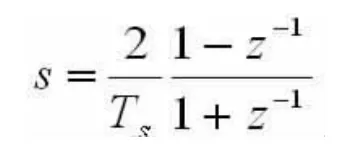
图3示出了模拟和数字积分器的方框图。

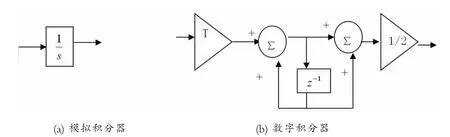
图3 模拟和数字积分器

将图2(a)中的1/s用数字积分器替代，得到图4的一阶数字环路低通滤波器模型。同样，二阶数字低通滤波器只需将图2(b)中的1/s用图3中的数字积分器代替，传递函数F(s)即可从s平面转换到z平面。

图4 一阶数字环路低通滤波器

图2,4中两种环路低通滤波器的参数通常根据表1进行选择，表中R为卫星的视距距离,给定环路滤波器噪声带宽凡便可以计算出自然频率ω0。实际应用中,可以根据设计要求来选取合适的环路低通滤波器

表1 环路低通滤波器特性

3 三阶锁相环参数设计

三阶锁相环环路滤波器的设计中，经常采用理想二阶滤波器模型，滤波器函数为：

锁相环开环方程为：

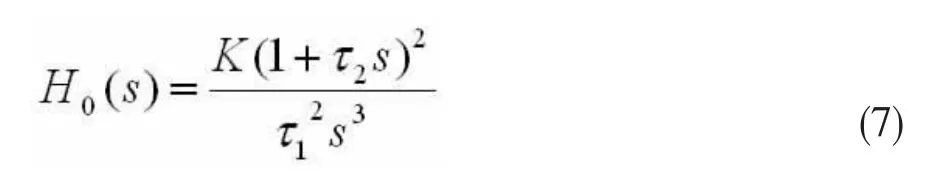
闭环方程为：

利用伯德法则，当开环增益为1时，其相位余量必须大于0，闭环才能稳定。根据开环方程，先计算临界频率：

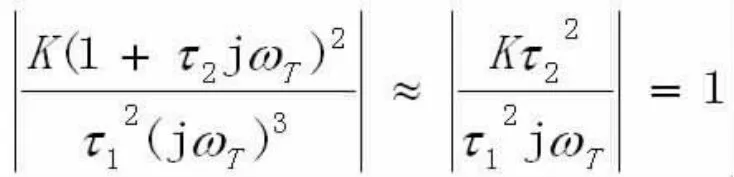
得到：

要求相位裕量大于0，则有：

根据定积分的计算方法[2]，得到：

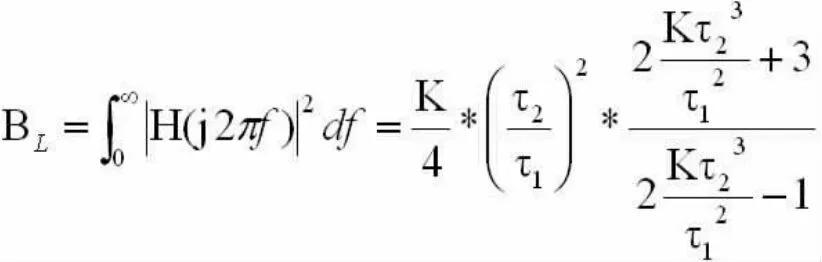
令

整理得：

由上式得到：

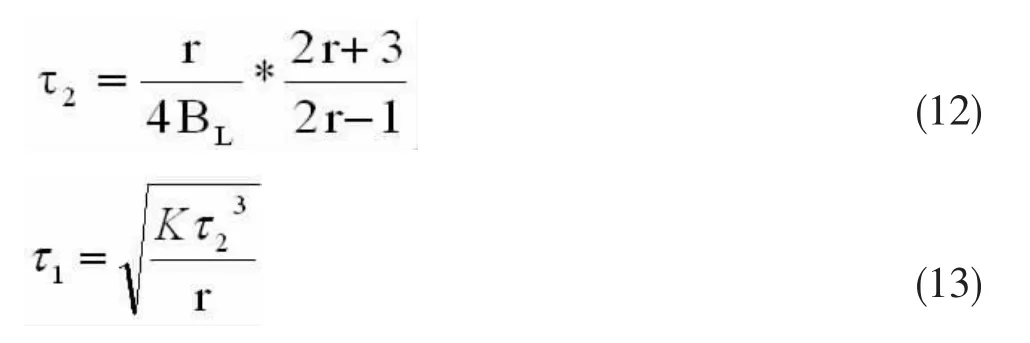
由(9)式和(10)式可得，r＞1是环路稳定的必要条件，本文取r=2进行下面的仿真。

将模拟锁相环转化为数字锁相环，采用并联数字滤波器结构，如图5所示。

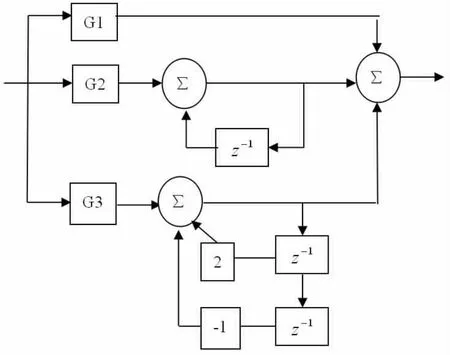
图5 二阶数字低通滤波器结构

其函数表达式为：

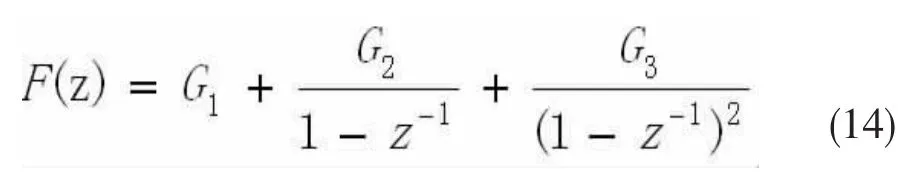
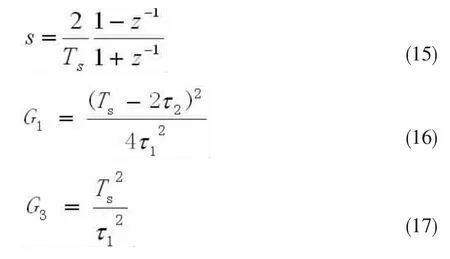
4 锁相环性能比较

为了研究锁相环路的特性，通常要研究三种类型的输入信号，一类是相位阶跃信号[3]

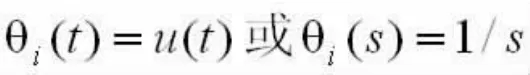
另一类是频率阶跃信号：

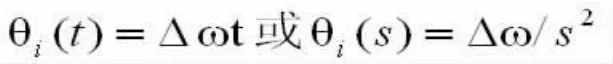
以及频率渐变信号：

绘制环路的响应曲线可以使用z变换得到的数字环路进行仿真，也可以通过反拉氏变换得到时域曲线。如二阶锁相环，滤波器函数为：

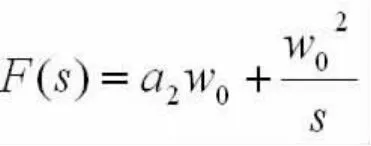
误差传递函数为：

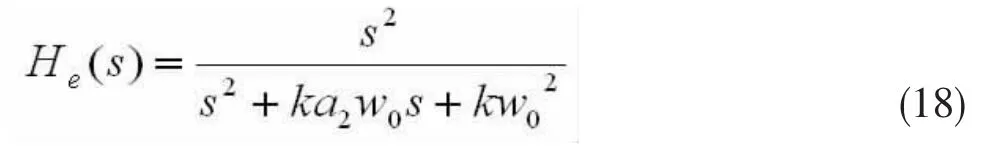
当输入为时，误差函数为：

根据表 1， 取 a2=1.414,k=1, 带宽 Bn=10Hz，则w0=18.9。

利用Matlab中的ilaplace（hs）函数，可以得到时域误差函数，m文件为：

且由图6可见，由数字环路仿真得到的曲线（根据图4，z变换）与通过反拉氏变换得到式(19)的时域曲线完全重合。

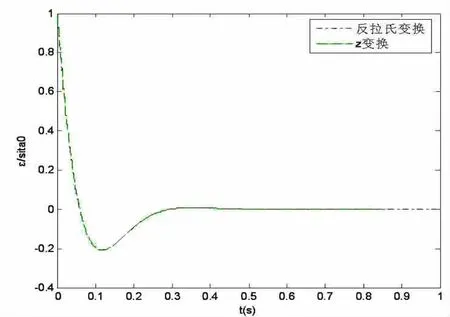
图6 z变换与反拉氏变换曲线图

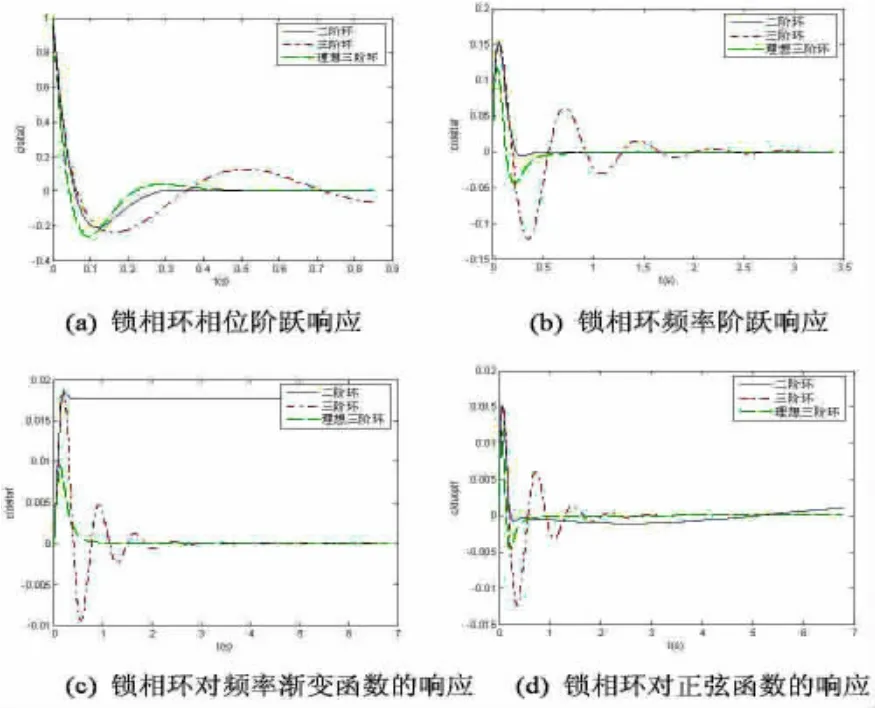
图7 锁相环输入响应

图7(a)为三种锁相环的相位阶跃响应，图7(b)为频率阶跃响应，图7(c)为频率渐变响应，图7(d)为正弦输入响应，正弦输入信号的频率为0.1Hz。锁相环带宽Bn均为 10Hz，对于理想三阶环，增益 k=0.5，r=2。

上述结果均为理想鉴相器条件下获得，从误差曲线观察，相似参数条件下两种构型的三阶环对相位阶跃和频率阶跃的响应效果不如二阶环，容易出现振荡或跟踪缓慢，而对于频率渐变响应，可以看出二阶环的稳态误差不为零，对于正弦输入响应，二阶环的误差在输入信号的频率为低于0.5Hz时不如两种三阶环，输入频率增加时，所有环路误差都将增大。

5 结束语

本文对三种锁相环路特性进行了推导，对各环路的相位阶跃响应、频率阶跃响应和正弦输入响应进行了对比，从对比结果观察，二阶锁相环路对于一般的相位阶跃及频率阶跃输入信号有很好的适应性，高阶锁相环路对具有频率渐变特性的输入信号适应性好，但需要合理的选择参数，避免出现环路振荡或收敛缓慢。