大跨山区钢桁梁悬索桥动力特性理论分析和试验研究

徐 朔，万 钰，吴文鹏

(1.湖南省交通科学研究院有限公司，湖南 长沙 410015；2.湘潭大学，湖南 湘潭 411105)

悬索桥不仅可以跨越大江大河，还能在山区、峡谷中发挥其一跨跨越的强大优势，相比钢箱梁悬索桥，钢桁加劲梁悬索桥在山区和峡谷中施工更方便，因此被山区跨峡谷桥梁所广泛采用[1-2]。大跨度悬索桥结构的力学特性决定了其具有独特的动力特性，基于环境激励，包括风载、地脉动、车辆及人群荷载等，悬索桥会产生自身特有振动现象，对大跨悬索桥结构进行动力试验测试能够验证结构的抗震与抗风性能，完善结构的设计理论，对大桥运营过程中的健康监测也可提供初始状态参数[3-5]。

本文工程背景为某山区主跨856 m的简支钢桁梁地锚式特大悬索桥，利用MIDAS CIVIL有限元软件建立其理论结构模型[6]，计算结构整体动力特性。在此基础上，采用模拟试验，测试结构动力特性，如结构各关键截面加速度、速度及动应变等。

1 工况概况

本桥主缆采用200 m+856 m+190 m跨径布置形式，中心线横向距离为2 800 cm，主跨垂径与跨径之比为1∶10。两边主缆各有索股127股，单束索股由127根φ5.15 mm平行镀锌钢丝组成。大桥共设置69对吊索，标准公称直径为56 mm，标准间距为1 200 mm。吊索上下端连接方式分别为骑跨式和销铰式连接。

本桥钢桁梁由主桁架、主横桁架、上下平联及抗风稳定板组成，钢桁梁宽2 800 cm，高650 cm，标准节段长1 200 cm。在桥塔下横梁处设竖向支座及横向抗风支座，两岸锚碇均采用重力式锚碇。

本桥索塔采用门式框架结构，由扩大基础、塔座、塔柱和横梁组成，两岸塔高分别为137.488 m和123.192 m。

本桥桥面系采用钢混组合结构形式，纵向工字梁与混凝土桥面板相结合，工字梁高0.63～0.86 m，长12 m，桥面板采用预制混凝土板，板长11.52 m，宽1.62 m，厚0.16 m，桥面板为连续结构，利用纵梁上的剪力钉在接缝处与纵梁相结合。大桥整体布置图如图1所示，横断面布置如图2所示。

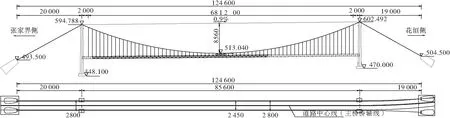
图1 桥梁结构整体布置图(单位：cm)

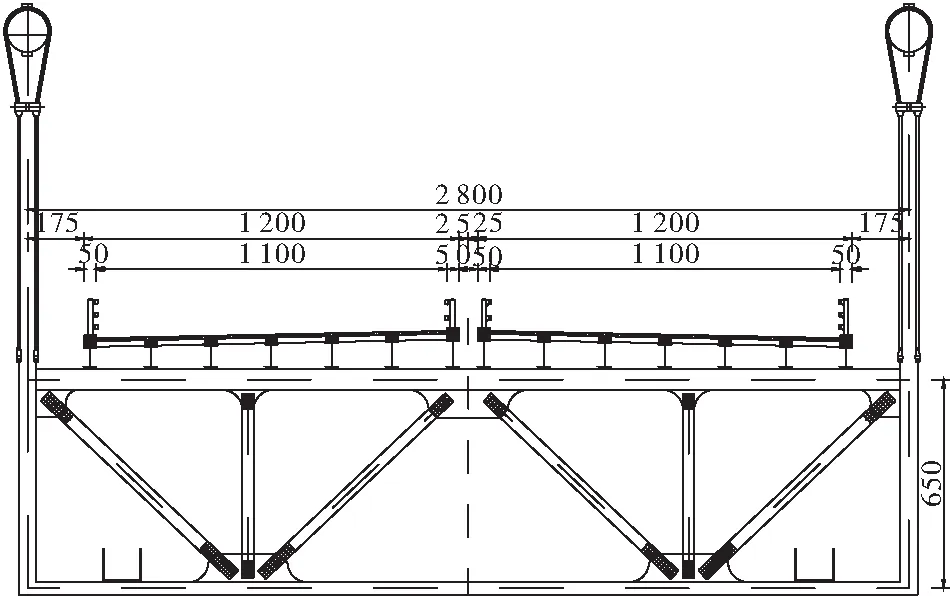
图2 桥梁结构横断面布置图(单位：cm)

2 有限元建模

在成桥状态下，对悬索桥的主缆线形及张力进行计算分析，使得理论分析模型在恒载作用下达到受力平衡状态，此时，主缆线形及张力逼近设计目标值，误差应在允许范围之内，此种平衡状态即为结构的初始平衡状态。本文采用MIDAS CIVIL软件计算出与相应设计目标值相符合的空缆线形，根据桥梁实际情况修正或调整模型结构、边界条件及荷载参数，对初始模型进行初始平衡状态分析计算，得到结构的精算模型，以此作为结构理论分析计算的基础[7]。

主缆及吊索为只受拉构件，在结构模型中采用索单元，计算刚度时考虑轴向拉力对结构刚度的影响，主缆的弹性模量采用了Ernst公式[4]修正。

(1)

式中:Eeq为主缆等效弹性模量;Ee为主缆有效弹性模量；γ为主缆线容重;l为主缆水平投影长度;σ为主缆初应力。

考虑到悬索桥加劲梁各杆件的尺寸较大，建模中采用梁单元而非桁架单元进行模拟，因桥面系对结构的竖向刚度影响较小，只考虑桥面系对结构的质量影响。因此，采用梁格模拟加劲梁各杆件，并将加劲梁各杆件及桥面系各部分的质量与重量等效布置于桥面。采用梁单元模拟悬索桥结构的索塔和塔横梁等构件，采用固结的方式模拟锚碇、索塔的边界条件影响，释放加劲梁的纵向位移和转动约束，仅在其竖向与横向进行约束，大桥结构模型如图3所示。

图3 桥梁结构有限元三维离散模型

3 振动测试与分析

大跨悬索桥因跨度大，质量相对较轻，结构体系较柔，对外界因素引起的振动更为敏感，所以对大桥结构进行动力特性测试及相关分析，对大桥今后运营过程中的风险控制显得尤为重要。因大跨悬索桥是一种柔性结构体系，运营过程中会产生较大的变形情况，从而在建立几何协调方程和受力平衡方程中有必要考虑大位移非线性特性。此外，由于悬索桥的安全系数较高，成桥状态下各构件的应力水平总体偏低，结构材料实际上多处于线弹性状态，因此大跨悬索桥的结构模型计算还需要考虑小应变情况下的大位移问题[4]。

为了解大桥结构的实际动力特性情况，以大桥理论计算模型为基础，采用脉动法对大桥结构的动力特性进行实桥测试。在封闭桥面交通后，并确保大桥周围无人为制造较大振动源的情况下，采用高灵敏度的拾振器测量桥梁结构在环境激励下的响应，再通过频谱分析和构建振动模型，计算桥梁结构低阶自振频率及其对应的结构振型[8-10]。

振动测试采用江苏东华仪器厂生产的DH5907A 无线振动测试系统对大桥结构进行振动测试，测试系统框图如4(a)所示。DWL-2100AP为双向低频速度传感器，选做参考点；DWL-3200AP为双向低频速度传感器，选做移动测点。DH5907A 无线振动测试系统的测试方法是选择一个测点为参考点，利用GPS同步授时技术，通过DHDAS数据采集软件分区测量各测点的振动信号，通过DHMA模态分析软件将采集到的数据通过傅里叶分解及参数识别获取各振动参数[11]，并将各测点数据整合图形化，输出桥梁结构振动图形，其测试系统实物如图4(b)所示。

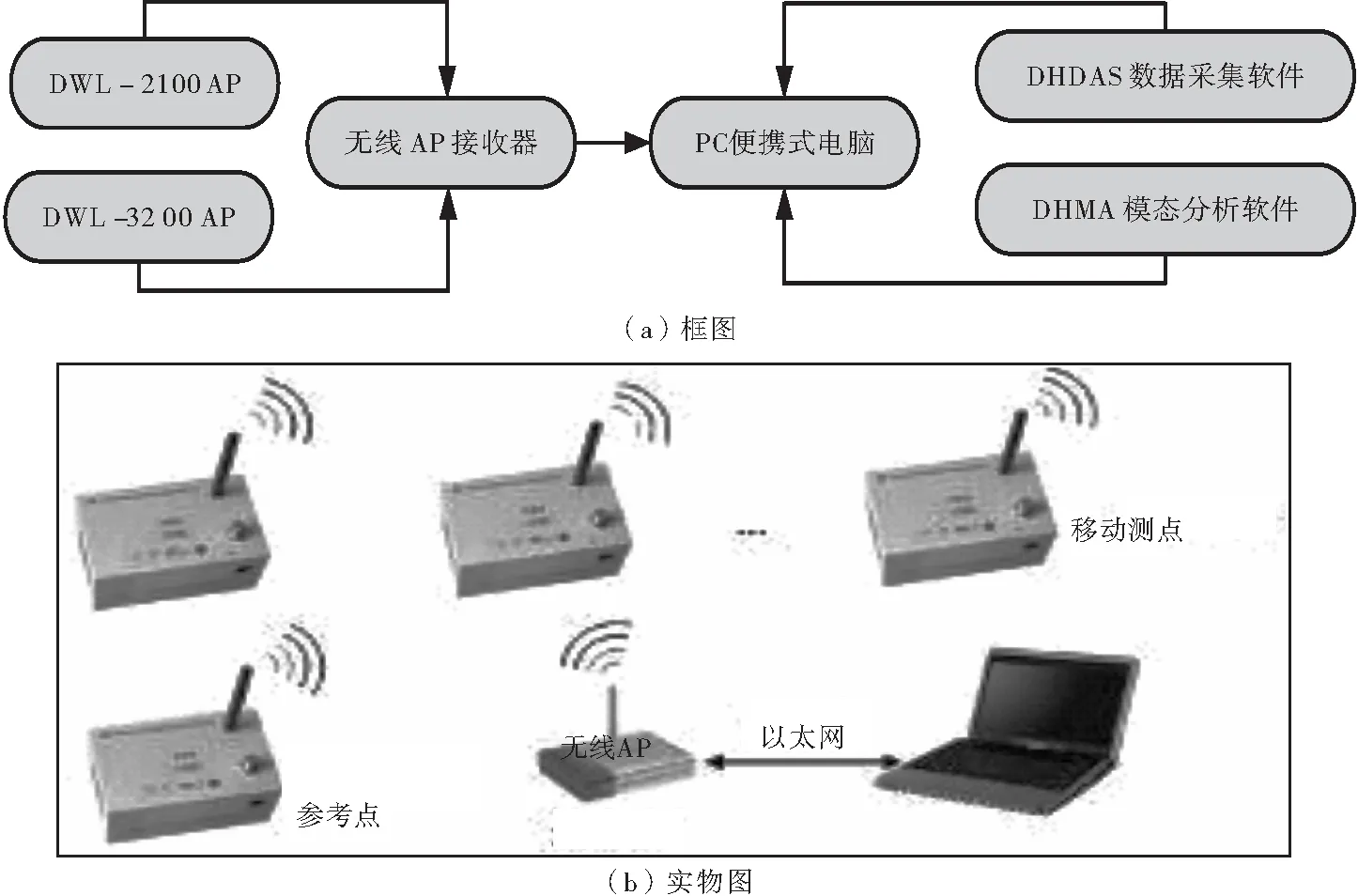
图4 模态测试系统框图和DH5907A无线振动测试系统实物图

通过实桥测试，取结构前6阶振动测试结果，将实测结果与理论计算结果进行对比分析，表1为自振频率实测值与理论计算值的对比，图5为振动图形的实测结果与理论计算结果的对比。

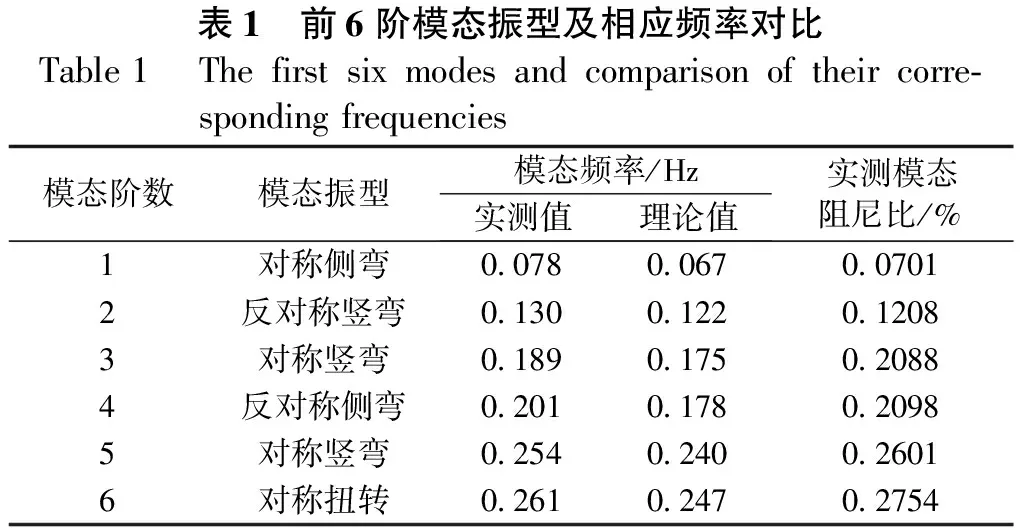
表1 前6阶模态振型及相应频率对比Table1 Thefirstsixmodesandcomparisonoftheircorre-spondingfrequencies模态阶数模态振型模态频率/Hz实测值理论值实测模态阻尼比/%1对称侧弯0.0780.0670.07012反对称竖弯0.1300.1220.12083对称竖弯0.1890.1750.20884反对称侧弯0.2010.1780.20985对称竖弯0.2540.2400.26016对称扭转0.2610.2470.2754

由表1和图5可知，悬索桥的前6阶的实测振动频率与理论计算频率吻合较好，前6阶自振频率中两者差别最大的为第1阶，其相对差值为16.4%；实测的前6阶结构振动图形与理论计算振动图形基本一致。同时，由表1可知，大桥结构前6阶自振频率均大于对应的理论分析频率，说明大桥整体刚度(纵向、横向、扭转)大于其设计刚度，满足设计要求。

图5 结构前6阶理论振型与实测模态振型对比

4 外界激励测式与分析

跳车与刹车作为外界激励信号分别激发结构的垂直振动和水平振动，通过拾振器拾取结构相应的响应信号，对实测响应信号进行处理，得到典型的波形图。本文试验中选用1辆40 t重的加载车，在预定激振位置，汽车后轮越过一根高15 cm的契形横木，车轮落下后立即停车，激发桥梁竖向振动，跳车试验示意如图6(a)所示；同样选用一辆40 t重的加载车，以60 km/h的速度匀速行驶至大桥跨中测试断面，制动减速至0，刹车试验示意如图6(b)所示。

跳车试验采用竖向加速度传感器采集结构的竖向振动信号，刹车试验采用应变计测量结构动应变信号。试验测试系统如图6(c)所示，跳车试验时，结构受垂直冲击力作用，测试系统输出的电压随时间变化的波形如图7(a)所示；刹车试验时，结构受水平冲击力的作用，其应变随时间变化的波形如图7(b)所示。

电压随时间变化的波形间接反映出结构竖向振动随时间变化的关系，由图7(a)电压时程图形中可以看出，结构竖向振动随时间呈现出周期性衰减，从振动最剧烈时刻到恢复平衡时刻经历了14.2 s，这表明大桥结构对竖向冲击力具有较强的吸收耗散能力。同时，由图7(b)可知，刹车试验时的动应变时程波形图呈现出典型动应变变化特征，大桥结构的最大动应变幅值为-23.5με。

图6 跳车试验和刹车试验示意图

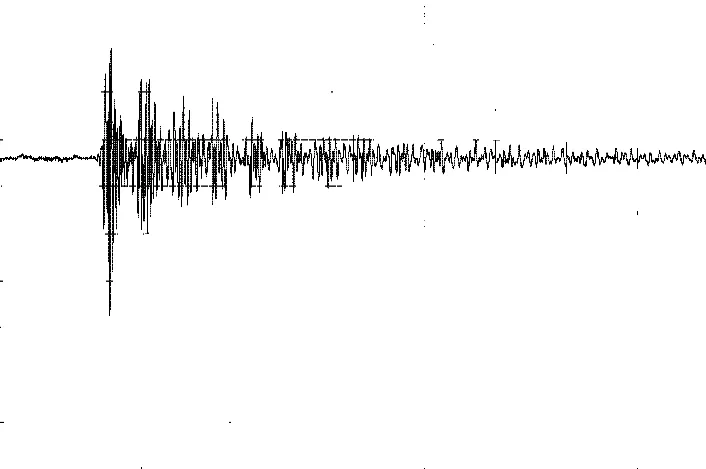
(a)跳车测试电压时程波形

6 结论

a.振动试验结果：① 该桥第1阶振型为横向对称侧弯，实测频率(0.078 Hz)大于其理论计算值(0.067 Hz)，成桥横向侧弯刚度大于其理论设计刚度；② 该桥第2阶振型为竖向反对称竖弯，实测频率(0.130 Hz)略大于其对应理论计算值(0.122 Hz)，实测值与理论计算值接近，成桥竖弯刚度与其对应理论设计刚度吻合较好；③ 该桥第6阶振型为横向扭转，实测频率(0.261 Hz)大于其对应理论设计值(0.247 Hz)，成桥横向扭转刚度大于其理论设计刚度；④ 大桥结构实测前6阶振动频率与对应理论计算值吻合较好，且实测值略大于理论计算值。另外，前6阶实测振型与相应理论计算振型一致，表明试验结果准确可靠，且大桥结构的整体刚度大于相应设计目标值。

b.跳车和刹车试验结果：结构在垂直方向冲击力作用下，振动信号呈现出周期性衰减且衰减迅速，表明大桥结构抗冲击能力较强，具有较强的能量耗散能力；结构在水平冲击力作用下，呈现出较好的动力受力性能，结构产生的最大动应变为-23.5με，在可接受的范围内。