赤石特大桥结构体系研究

2020-07-14龙海滨刘汉彪贺耀北

公路工程 2020年3期

张铭，龙海滨，刘汉彪，贺耀北

(1.湖南省交通规划勘察设计院有限公司，湖南长沙 410008;2.湖南大学土木工程学院，湖南长沙 410016)

1 工程概况

赤石特大桥主桥跨径布置为：165 m+3×380 m+165 m；桥面全宽28.0 m，两侧锚索区各1.75 m，两侧无辅助墩，索塔编号为5号～8号，其索塔高度分别为254.63、274.13、281.63、266.13 m，桥面至地面最大高差182 m。索塔两侧均布置23对斜拉索，纵向呈扇形布置，中间6号、7号索塔均采用塔、梁、墩固结体系，两侧5号、8号索塔塔、墩固结，主梁以下设置单排支座，采用支承体系。

主梁采用单箱四室斜腹板箱型断面，其标准断面中心高度为3.2 m，箱梁顶部宽度为27.5 m，两侧风嘴宽度均为0.25 m。箱梁底板全宽为16.17 m，斜腹板宽度为4.62 m[1]。

与常规双塔斜拉桥结构相比，赤石特大桥边跨无辅助墩，中塔没有尾锚索约束，其主梁与索塔的刚度将会减弱[1]。而主梁和索塔的刚度是多塔斜拉桥整体变形的决定性因素，中塔在活载作用下，其位移和内力均较大，主梁活载作用下的位移明显增大，其竖向刚度降低，而且塔数越多，中间塔离过渡墩越远，刚度越弱[3-5]。

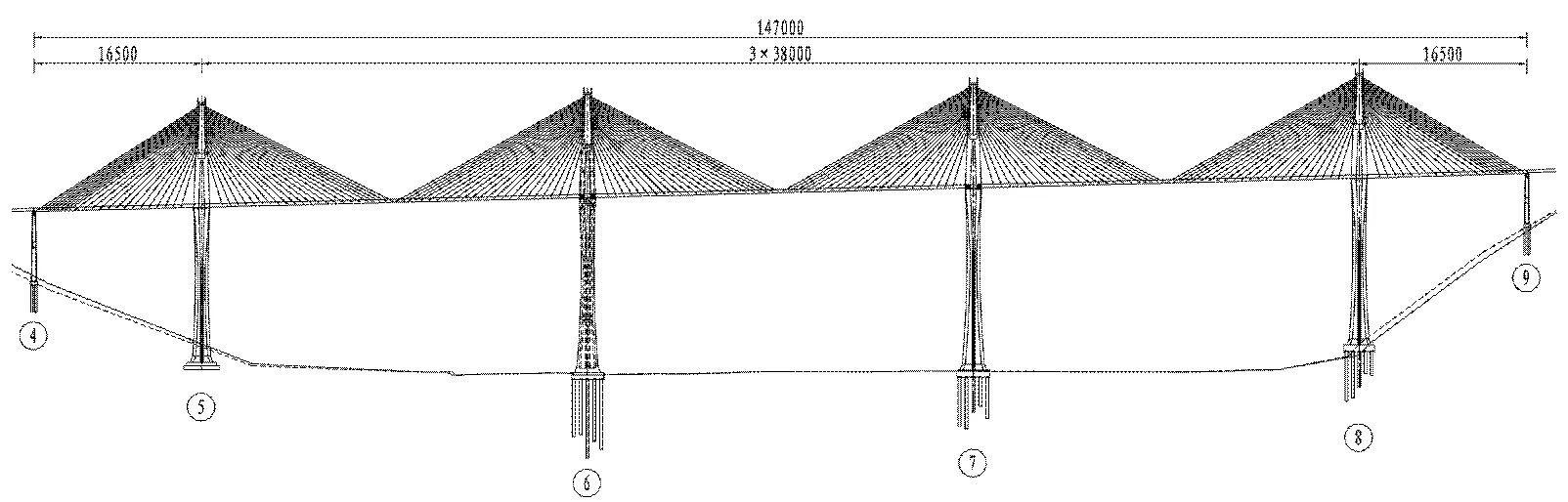
(a)桥型布置纵断面图

赤石特大桥结构体系设计的重点是，在全桥无辅助墩和不增设斜拉索的情况下，解决索塔结构的受力以及中跨主梁活载作用下的变形问题[6]。本文研究的赤石特大桥由于超高墩的存在，索塔结构受力和中跨主梁的活载变形过大的问题更加严重。除纵坡外，本桥结构基本对称，限于篇幅，本文取1/2结构的结果进行分析。

2 有限元模型的建立

利用有限元软件MIDAS Civil建立空间“鱼骨梁”杆系模型，全桥共划分节点1 476个，单元1 821个。结构体系为边塔半漂浮、中塔塔梁墩固结。

主梁和索塔分别采用C55、C50混凝土，斜拉索采用镀锌钢绞线。主梁和索塔采用梁单元模拟，斜拉索采用仅受拉桁架单元模拟。索塔塔底固结，过渡墩位置约束竖向和横向位移，斜拉索与主梁及主塔刚性连接，边塔半漂浮通过下塔柱与主梁之间设置限制竖向和横向位移的主从约束来实现，中塔固结通过将下塔柱分别与主梁及上塔柱进行刚性连接来实现。模型施加的荷载为车道荷载和温度荷载，其中车道荷载采用单车道加载，增大系数为3.68，温度荷载考虑20 ℃整体升温。

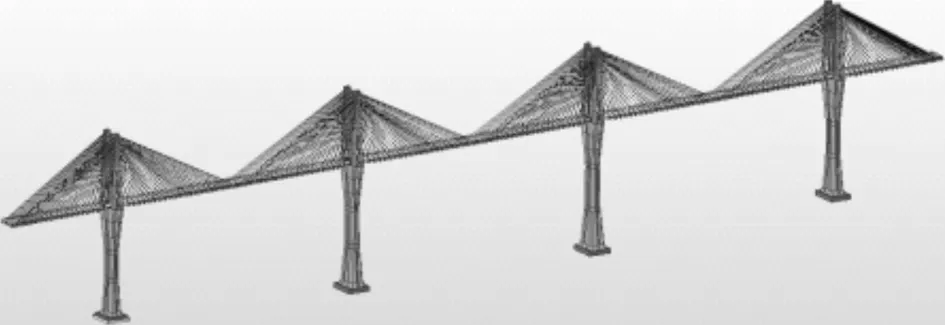
图2 赤石大桥(双曲线塔)有限元计算模型

3 索塔选型

为选择合理的索塔结构形式，通过与常规H型索塔对比分析，研究双曲线超高墩索塔的结构特性。建立H型索塔的有限元模型，除索塔形式外，其余主要材料、设计参数及体系均不变。

图3 赤石大桥(H塔)有限元计算模型

3.1 活载作用的静力比较分析

对赤石特大桥各个主要受力结构(主梁、索塔、斜拉索)在运营阶段关键位置的力学特性(应力、位移)进行比较分析,见表1～表4。

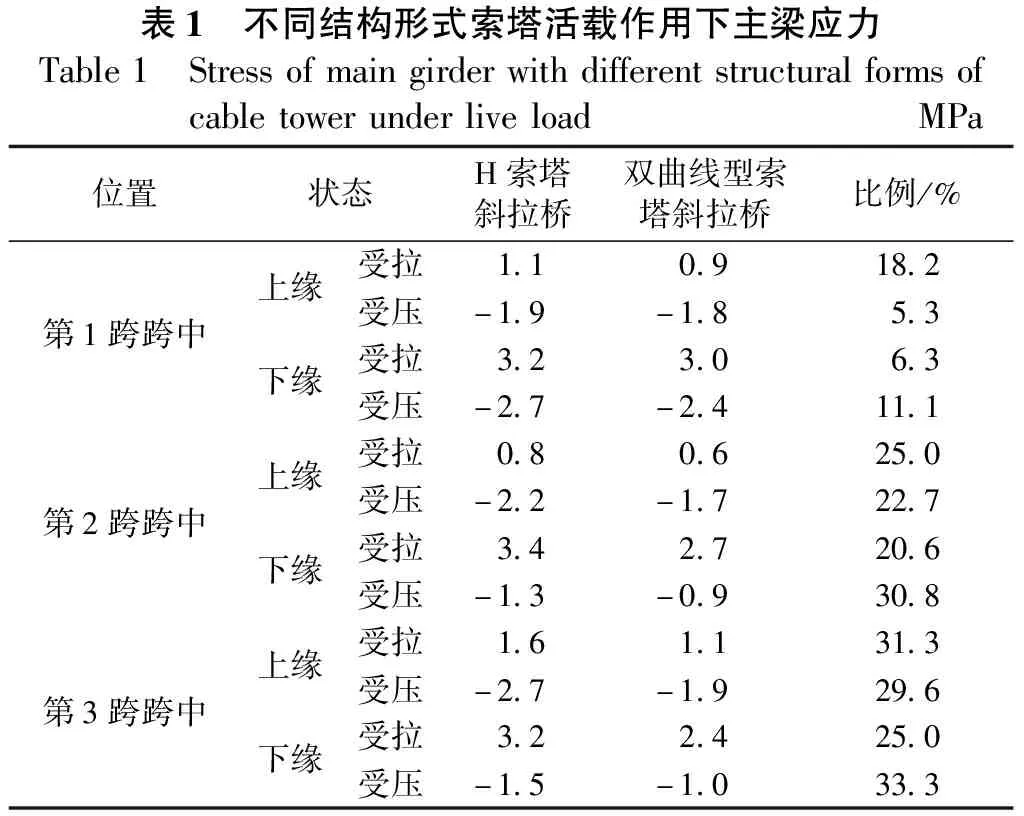
表1 不同结构形式索塔活载作用下主梁应力Table1 StressofmaingirderwithdifferentstructuralformsofcabletowerunderliveloadMPa位置状态H索塔斜拉桥双曲线型索塔斜拉桥比例/%上缘受拉1.10.918.2第1跨跨中受压-1.9-1.85.3下缘受拉3.23.06.3受压-2.7-2.411.1上缘受拉0.80.625.0第2跨跨中受压-2.2-1.722.7下缘受拉3.42.720.6受压-1.3-0.930.8上缘受拉1.61.131.3第3跨跨中受压-2.7-1.929.6下缘受拉3.22.425.0受压-1.5-1.033.3

由表1数据可知，采用双曲线超高墩的赤石特大桥其关键位置的主梁应力值明显小于H索塔斜拉桥的应力值；第2、第3跨跨中应力值下降比例较大，均超过了20%，其中第3跨跨中下缘压应力值下降比例最大，约为33.3%。

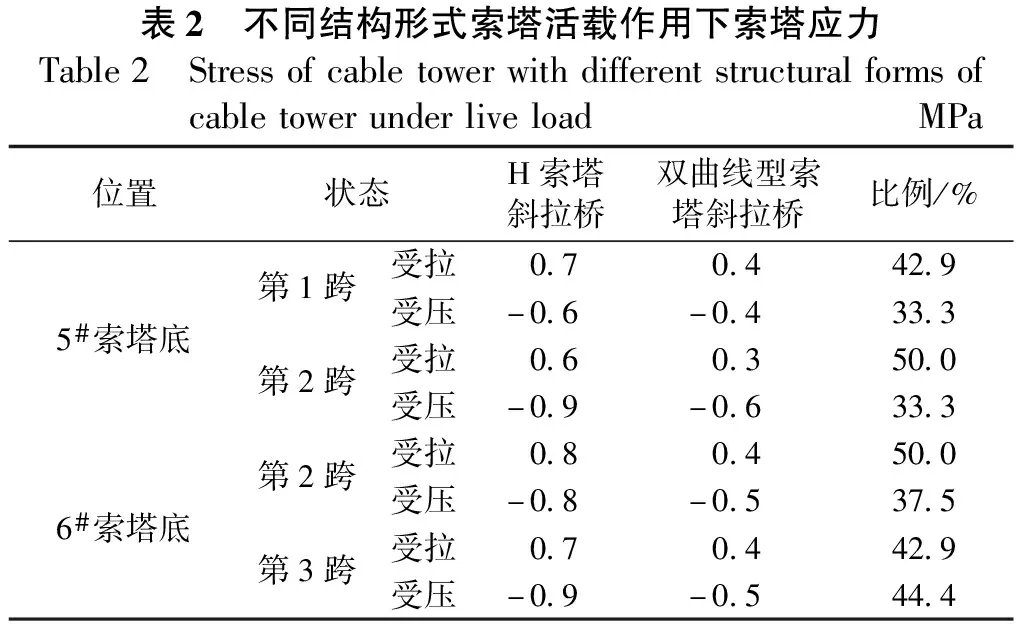
表2 不同结构形式索塔活载作用下索塔应力Table2 StressofcabletowerwithdifferentstructuralformsofcabletowerunderliveloadMPa位置状态H索塔斜拉桥双曲线型索塔斜拉桥比例/%第1跨受拉0.70.442.95#索塔底受压-0.6-0.433.3第2跨受拉0.60.350.0受压-0.9-0.633.3第2跨受拉0.80.450.06#索塔底受压-0.8-0.537.5第3跨受拉0.70.442.9受压-0.9-0.544.4

由表2数据可知，采用双曲线超高墩的赤石特大桥其塔底的应力值远低于H型索塔斜拉桥的应力值，降低的幅度超过30%。其中5#和6#索塔的塔底在第2跨侧边缘拉应力值下降比例最大，约为50.0%。

由表3数据可知，采用双曲线超高墩的赤石特大桥在活载作用下，其背索应力值小于H型索塔斜拉桥的应力值，降低的幅度超过10%。

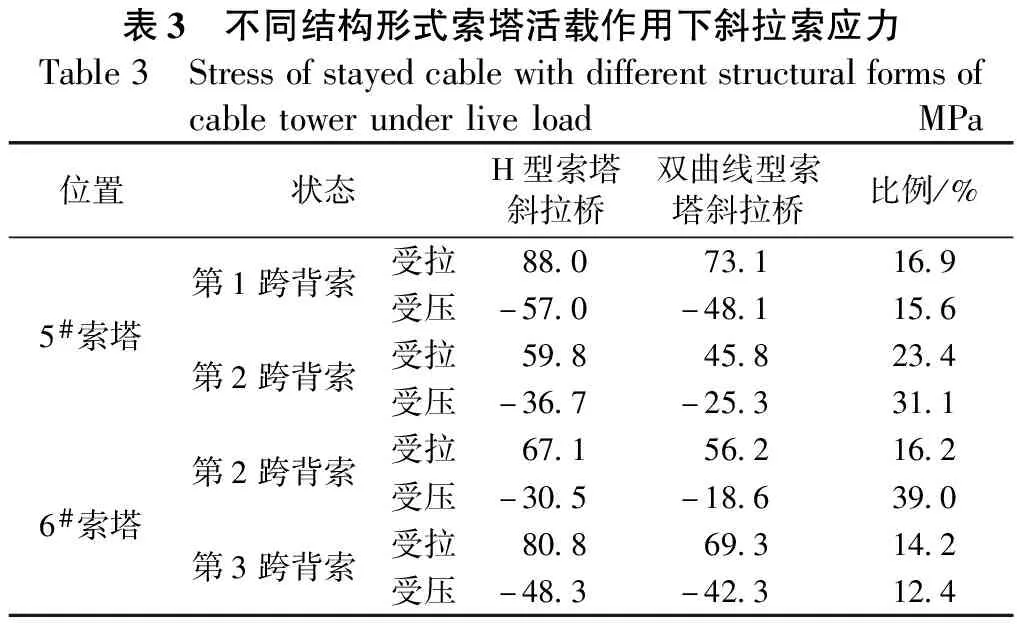
表3 不同结构形式索塔活载作用下斜拉索应力Table3 StressofstayedcablewithdifferentstructuralformsofcabletowerunderliveloadMPa位置状态H型索塔斜拉桥双曲线型索塔斜拉桥比例/%第1跨背索受拉88.073.116.95#索塔受压-57.0-48.115.6第2跨背索受拉59.845.823.4受压-36.7-25.331.1第2跨背索受拉67.156.216.26#索塔受压-30.5-18.639.0第3跨背索受拉80.869.314.2受压-48.3-42.312.4

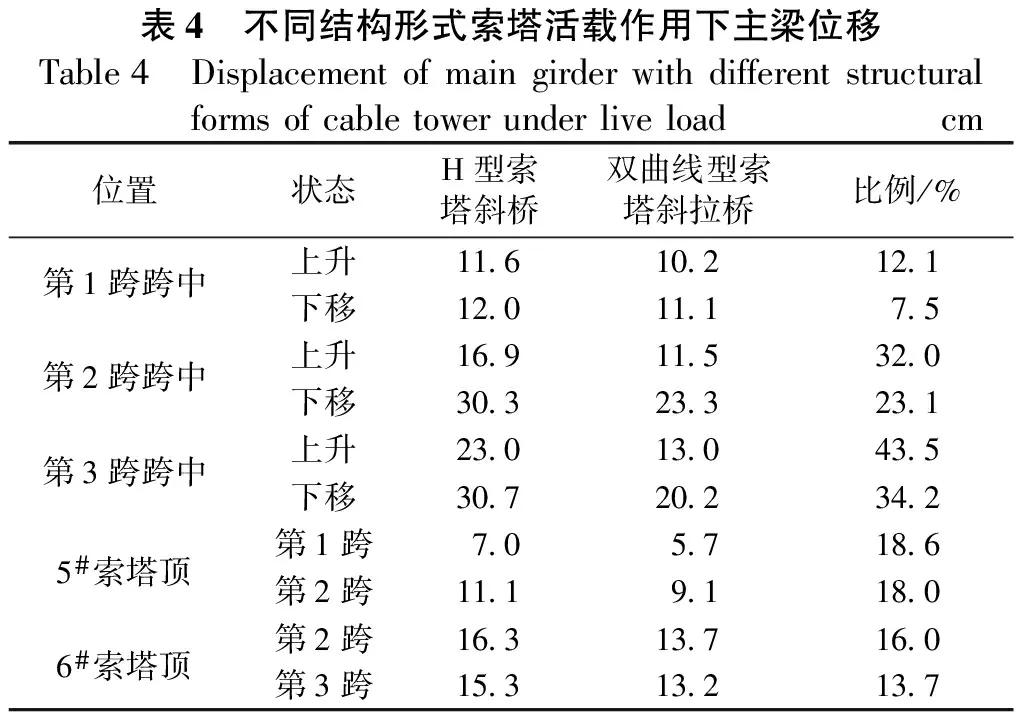
表4 不同结构形式索塔活载作用下主梁位移Table4 Displacementofmaingirderwithdifferentstructuralformsofcabletowerunderliveloadcm位置状态H型索塔斜桥双曲线型索塔斜拉桥比例/%第1跨跨中上升11.610.212.1下移12.011.17.5第2跨跨中上升16.911.532.0下移30.323.323.1第3跨跨中上升23.013.043.5下移30.720.234.25#索塔顶第1跨7.05.718.6第2跨11.19.118.06#索塔顶第2跨16.313.716.0第3跨15.313.213.7

由表4数据可知，越往中跨，主梁的竖向位移值和塔顶的水平位移值越大，符合离过渡墩越远，索塔刚度越小的多塔斜拉桥受力特点。

相比H型索塔，采用双曲线超高墩的赤石特大桥主梁竖向位移值明显降低，下降的幅度为7.5%～43.5%，且下降幅度从边跨往中跨逐渐加大。索塔塔顶水平位移下降幅度在13.7%和18.6%之间，中塔下降幅度比边塔下降幅度更大。

根据静力计算结果可知，采用双曲线超高墩的赤石特大桥其主梁、桥塔、拉索受力性能优于H型索斜拉桥，说明采用双曲线超高墩索塔的赤石特大桥设计优于采用常规H型索塔斜拉桥。

3.2 索塔数量

在赤石特大桥的设计过程中，为研究索塔数量变化对桥梁结构刚度的影响，以原桥为基本模型，分别采用双塔、三塔、五塔和六塔等4种多塔斜拉桥结构与原桥结构进行比较分析，分析模型与计算结果如图4～表6所示。

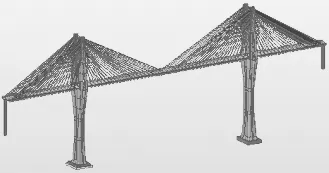
(a)双塔斜拉桥(165+2x380+165)m

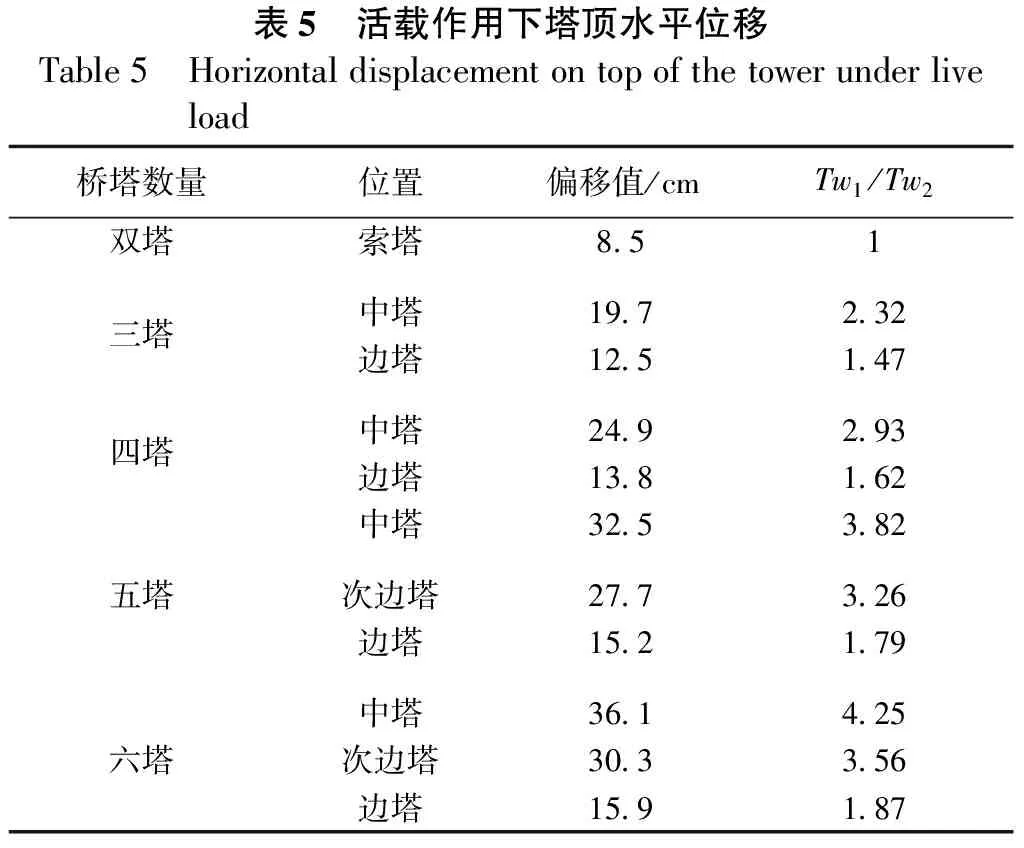
表5 活载作用下塔顶水平位移Table5 Horizontaldisplacementontopofthetowerunderliveload桥塔数量位置偏移值/cmTw1/Tw2双塔索塔8.51三塔中塔19.72.32边塔12.51.47四塔中塔24.92.93边塔13.81.62中塔32.53.82五塔次边塔27.73.26边塔15.21.79中塔36.14.25六塔次边塔30.33.56边塔15.91.87

由表5数据可知，塔数在双塔增加到六塔的过程中，在活载作用下，塔顶水平位移持续增大，双塔塔顶水平位移为8.5 cm，但六塔中塔塔顶位移已达到了36.1 cm。三塔到六塔斜拉桥的边塔水平位移为双塔斜拉桥的1.47倍到1.87倍，中塔水平位移为2.32倍到4.25倍，随着塔数的增加，索塔的刚度不断降低，且中塔降低幅度明显较边塔大。

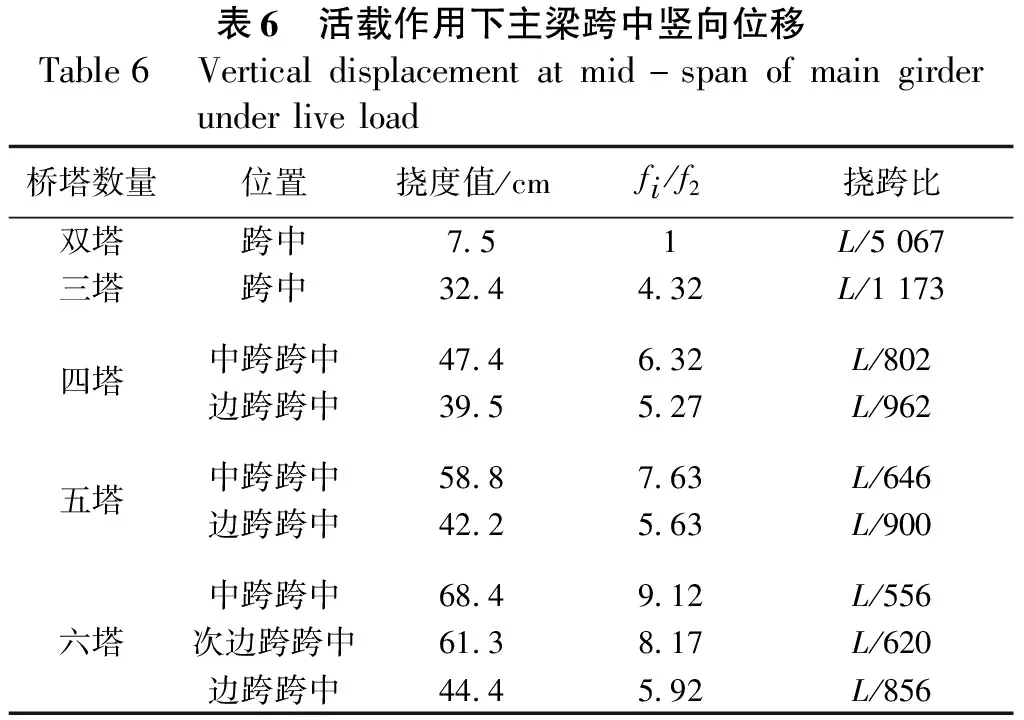
表6 活载作用下主梁跨中竖向位移Table6 Verticaldisplacementatmid-spanofmaingirderunderliveload桥塔数量位置挠度值/cmfi/f2挠跨比双塔跨中7.51L/5067三塔跨中32.44.32L/1173四塔中跨跨中47.46.32L/802边跨跨中39.55.27L/962五塔中跨跨中58.87.63L/646边跨跨中42.25.63L/900中跨跨中68.49.12L/556六塔次边跨跨中61.38.17L/620边跨跨中44.45.92L/856

由表6数据可知，塔数在双塔增加到六塔的过程中，在活载作用下，任意跨跨中的挠度均明显增大，尤其是中跨和次边跨跨中挠度值的增加幅度明显大于边跨的跨中挠度值。

从挠跨比来看，赤石特大桥采用双塔、三塔和四塔斜拉桥结构时，其中跨跨中挠跨比最大为L/802，满足高墩多塔斜拉桥挠跨比小于L/650的限值的要求。但索塔数量为5个和6个时，其跨中挠跨比最大为L/646，超过限值要求。因此当设计参数及体系均一致时，赤石特大桥索塔数量不能超过4个，赤石特大桥的索塔数量选择是合适的。

4 结构参数分析

由于中塔没有尾锚索限制其变形，外力作用下的多塔斜拉桥中塔往往水平位移较大，导致整体结构刚度较小。为合理设计其刚度，对影响多塔斜拉桥刚度的主要参数进行计算和分析。赤石特大桥在设计过程中对梁墩连接方式、索塔刚度和主梁刚度进行了对比分析，并择优选取相关尺寸。

4.1 塔梁墩连接方式

为研究多塔斜拉桥塔梁墩连接方式对结构刚度的影响，以赤石特大桥主桥为基本模型，采用与赤石特大桥相同的布跨和结构形式，将塔梁墩的连接方式分别采用①四塔均塔梁墩固结体系；②四塔均半漂浮体系；③四塔均全漂浮体系；④两边塔半漂浮体系、两中塔塔梁墩固结体系(简称：四塔固结、四塔半飘、四塔全飘、双固双半)。

由表7可知，活载与温度叠加作用下，固结体系塔根主梁弯矩最大，双固双半塔根主梁弯矩次之，四塔半漂和四塔全漂塔根主梁弯矩最小，即当塔根处有较大约束时，塔根主梁弯矩增大，且约束作用越大，塔根主梁弯矩越大；活载与温度叠加作用下，固结体系主梁跨中弯矩最小，双固双半跨中弯矩次之，四塔半漂和四塔全漂跨中弯矩最大，即当主梁有较大约束时，主梁跨中弯矩减小，且约束作用越大，主梁跨中弯矩越小；塔梁墩固结可以有效的降低跨中的正弯矩，同时在固结处有较大的负弯矩。采用双固双半可以同时结合固结与漂浮的优点，弱化二者的缺点。

表7 活载+温度作用下不同结构体系的主梁弯矩Table7 Momentofmaingirderwithdifferentstructuralsys-temsunderliveloadandtemperature(kN·m)位置状态四塔固结四塔半漂四塔全漂双固双半第1跨跨中上缘受拉23888422564504636797下缘受拉423985588154870512935#塔根上缘受拉75786406422113137801下缘受拉73799141803648211143第2跨跨中上缘受拉14555312963093520465下缘受拉432246179361801503966#塔根上缘受拉73977372581954733538下缘受拉44275118353435327429第3跨跨中上缘受拉19407486494815924349下缘受拉43104702017017847391

由表8可知，在活载与温度叠加作用下，采用固结体系和双固双半体系的主梁位移较四塔半漂(四塔全漂)体系分别小了56%、44%，说明采用固结体系或双固双半体系其整体刚度远大于采用四塔半漂或四塔全漂体系的多塔斜拉桥。

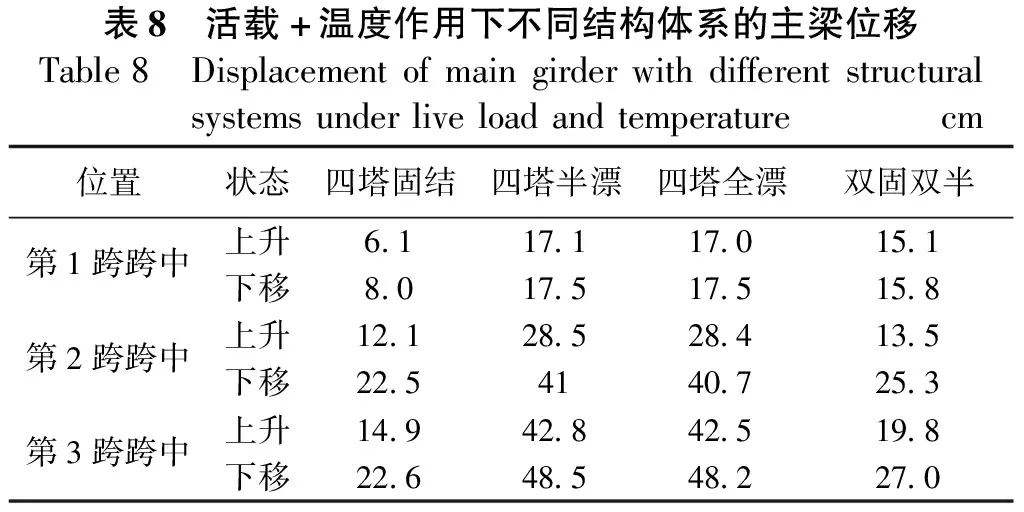
表8 活载+温度作用下不同结构体系的主梁位移Table8 Displacementofmaingirderwithdifferentstructuralsystemsunderliveloadandtemperaturecm位置状态四塔固结四塔半漂四塔全漂双固双半第1跨跨中上升6.117.117.015.1下移8.017.517.515.8第2跨跨中上升12.128.528.413.5下移22.54140.725.3第3跨跨中上升14.942.842.519.8下移22.648.548.227.0

由以上分析可知，赤石特大桥采用中塔与主梁固结，边塔和主梁分离的结构体系是比较合理的，该种结构体系结合了固结体系结构整体刚度大和漂浮体系保证顺桥向结构的自由变形的特点。

4.2 塔壁厚度

为研究多塔斜拉桥索塔刚度对结构刚度的影响，将索塔壁厚分别采用3种厚度进行比较分析，择优选择尺寸。其厚度分别为厚度A(180 cm)、厚度B(210 cm)和厚度C(150 cm)，断面示意图见图5。

在不同塔壁厚度下，主梁下挠值和索塔偏位值变化较小，主梁变化值最大不超过0.3 cm，约占主梁下挠值的2%。塔顶变化值最大不超过0.6 cm，约占塔顶偏位的4%。索塔壁厚对整体刚度等影响较小，壁厚由混凝土应力及稳定性等因素控制，最终赤石特大桥壁厚采用180 cm,见表9。

4.3 主梁顶底板厚度

(a)厚度A

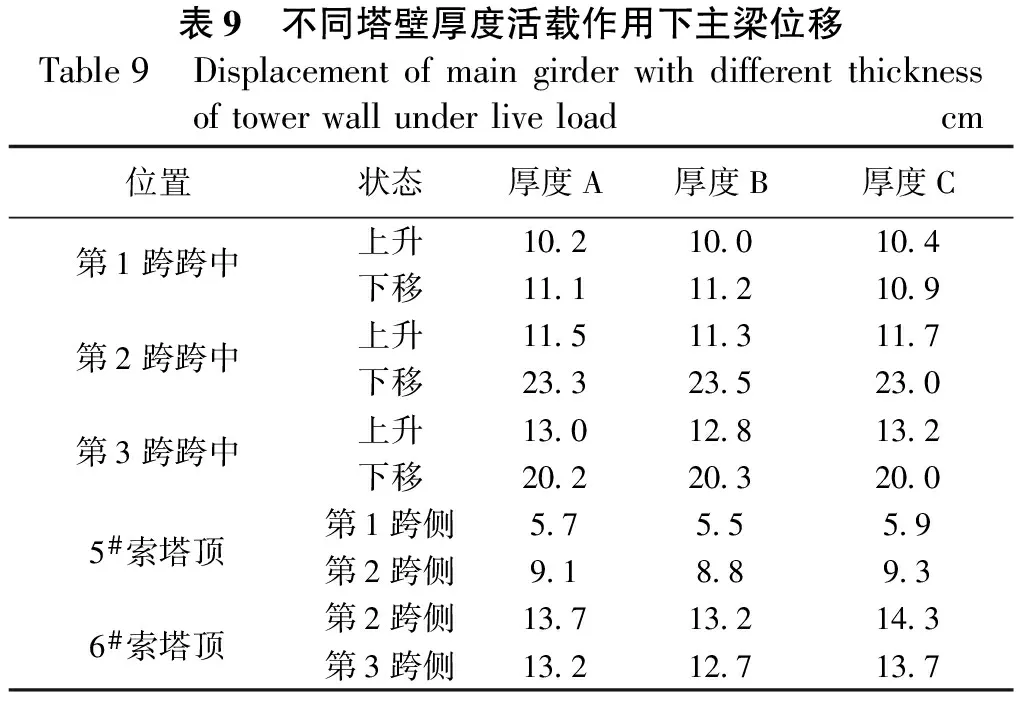
表9 不同塔壁厚度活载作用下主梁位移Table9 Displacementofmaingirderwithdifferentthicknessoftowerwallunderliveloadcm位置状态厚度A厚度B厚度C第1跨跨中上升10.210.010.4下移11.111.210.9第2跨跨中上升11.511.311.7下移23.323.523.0第3跨跨中上升13.012.813.2下移20.220.320.05#索塔顶第1跨侧5.75.55.9第2跨侧9.18.89.36#索塔顶第2跨侧13.713.214.3第3跨侧13.212.713.7

为研究多塔斜拉桥塔主梁刚度对结构刚度的影响，将主梁顶底板厚度分别采用尺寸A：(28 cm)、尺寸B(25 cm)和尺寸C(30 cm)进行比较分析，择优选择尺寸。

不同主梁刚度下，尺寸B从边跨支点到边跨跨中、中跨跨中附近的弯矩绝对值比尺寸A的增大，增大量约为主梁弯矩的10%以下，其他位置的弯矩绝对值均减小，减小量约为主梁弯矩的14%以下。尺寸C不论正负弯矩，其弯矩绝对值比尺寸A均增大，边跨跨中的正负弯矩绝对值增大量分别为23%、40%左右，墩顶位置正负弯矩绝对值增大量分别为7%，15%左右，中跨跨中正负弯矩增大量约为22%、12%左右,见图6。

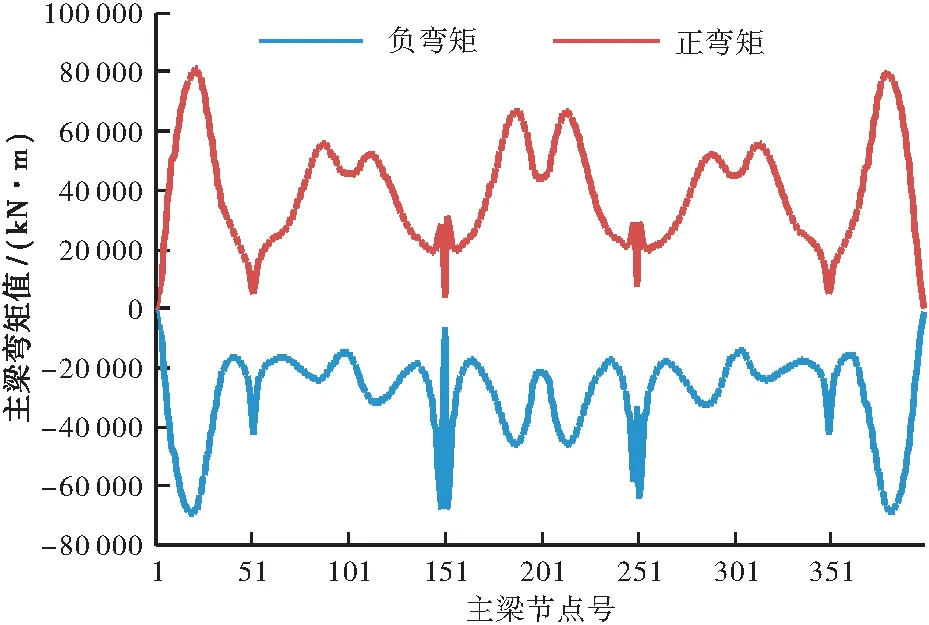
(a)尺寸A

不同的主梁刚度下，尺寸B关键位置的主梁位移值相对尺寸A均有所增大，最大增大量为2.3 cm，约占主梁位移值的10%。尺寸C关键位置的主梁位移值与尺寸A较为接近，最大差值约为4%。

尺寸A和尺寸C在塔顶的水平位移较为接近，差别仅为1 mm，尺寸B的塔顶水平位移相对尺寸A均有所增加，最大差值约为19%，一般在10%以下,见表10。

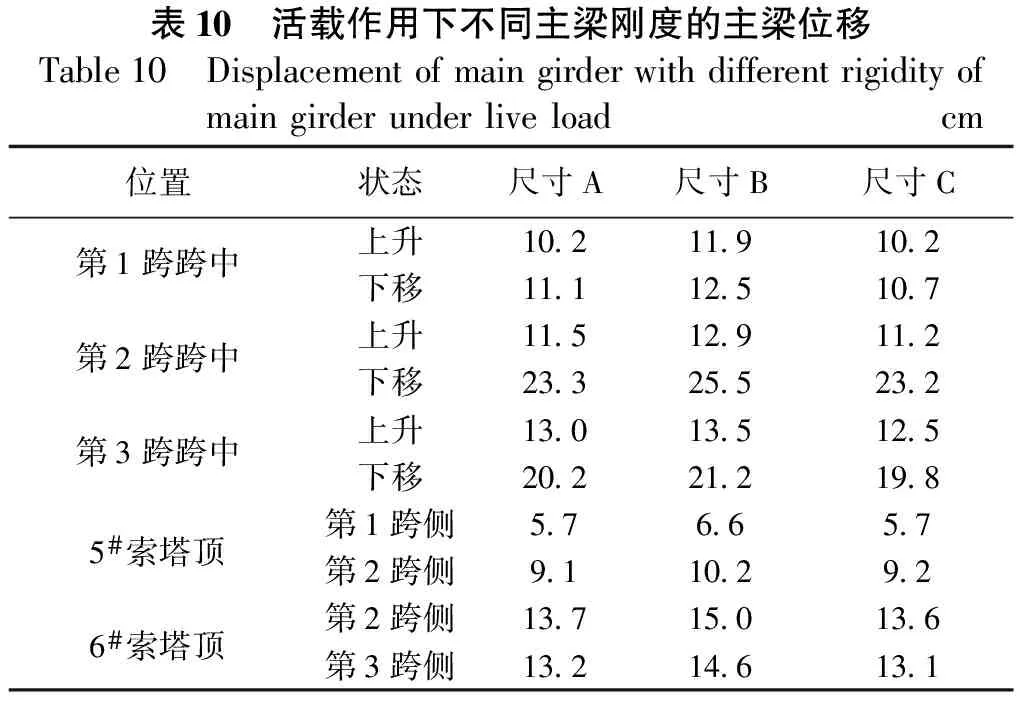
表10 活载作用下不同主梁刚度的主梁位移Table10 Displacementofmaingirderwithdifferentrigidityofmaingirderunderliveloadcm位置状态尺寸A尺寸B尺寸C第1跨跨中上升10.211.910.2下移11.112.510.7第2跨跨中上升11.512.911.2下移23.325.523.2第3跨跨中上升13.013.512.5下移20.221.219.85#索塔顶第1跨侧5.76.65.7第2跨侧9.110.29.26#索塔顶第2跨侧13.715.013.6第3跨侧13.214.613.1

从上述结果可知，随着主梁刚度的增大，结构活载变形减小，刚度增加，但增加幅度较小，主梁顶底板厚度对结构整体刚度影响较小。25 cm顶底板厚度不满足纵向预应力混凝土保护层厚度要求，采用30 cm顶底板厚度，将会造成材料的浪费，最终赤石特大桥顶底板厚度采用28 cm。