垂直起降运载器着陆支架总体设计与布局优化

朱冠宁，聂 宏,2，张 明,2，陈 力

(1.南京航空航天大学飞行器先进设计技术国防重点科学实验室，江苏 南京 210016)(2.南京航空航天大学机械结构力学及控制国家重点实验室，江苏 南京 210016)

可重复使用运载器与传统的一次性运载火箭不同，它从地面起飞并且完成预定发射任务后,全部或部分返回并安全着陆,经过检修维护与燃料加注后能够再次执行新的发射任务。可重复使用运载器通过多次利用运载器的箭体、发动机以及重要的电气设备等，实现运载器生产与发射成本的降低[1]。

垂直起降可重复使用运载器是众多的可重复使用运载器中的一种，其特点是垂直起飞、垂直降落，充分继承了运载火箭的技术优点。其中，垂直起降可重复使用运载器的成功运用需要得到以下几个关键技术的支持：发动机多次启动技术、发动机大范围推力调节技术、高精度导航及姿态控制技术、再入返回热环境预示和防护技术、栅格舵气动控制技术、高可靠着陆缓冲机构技术、多次启动推进剂管理技术和返场无拆卸快速检测与维护技术[2]。

着陆支架是一种新型的着陆缓冲机构，其具有可收放、可重复使用、缓冲效率高、着陆稳定性好、占用空间少等优点。在运载器飞行的上升阶段，着陆支架通过锁定装置紧固收拢在运载器表面，内部的着陆缓冲机构收藏在防热外壳内。在运载器返回着陆阶段，着陆支架在气压控制系统的驱动下，迅速展开、锁定，完成着陆缓冲之前的所有部署。运载器在着陆时，利用缓冲器吸收着陆时产生的能量，并降低着陆冲击产生的过载，最终达到运载器软着陆、可回收的目的[3]。

本文参照Space-X公司的Falcon-9运载器着陆支架的构型[4]，提出了一种着陆支架总体布局的设计方法，并对总体布局的设计参数进行优化。在ADAMS中建立着陆支架的参数化动力学模型，将两组设计参数分别代入动力学模型，对着陆支架的关键节点载荷、运载器过载、着陆稳定性等动力学响应进行对比验证。

1 着陆支架总体布局设计

选用外翻式着陆支架作为垂直起降可重复使用运载器的软着陆系统设计方案。根据着陆支架的设计要求，结合运载器内部的结构，将着陆支架中心对称布置于箭体四周。中心对称式的布局使得外翻式的着陆支架在姿态偏差、速度偏差以及侧风等非对称载荷条件下具有更好的稳定性。其结构形式如图1所示。

着陆支架主着陆腿1用于着陆支架的展开锁定以及吸收运载器着陆冲击时产生的能量；副着陆腿2与主着陆腿互相配合，完成着陆支架的收放；运载器的箭体3与着陆支架相连接。

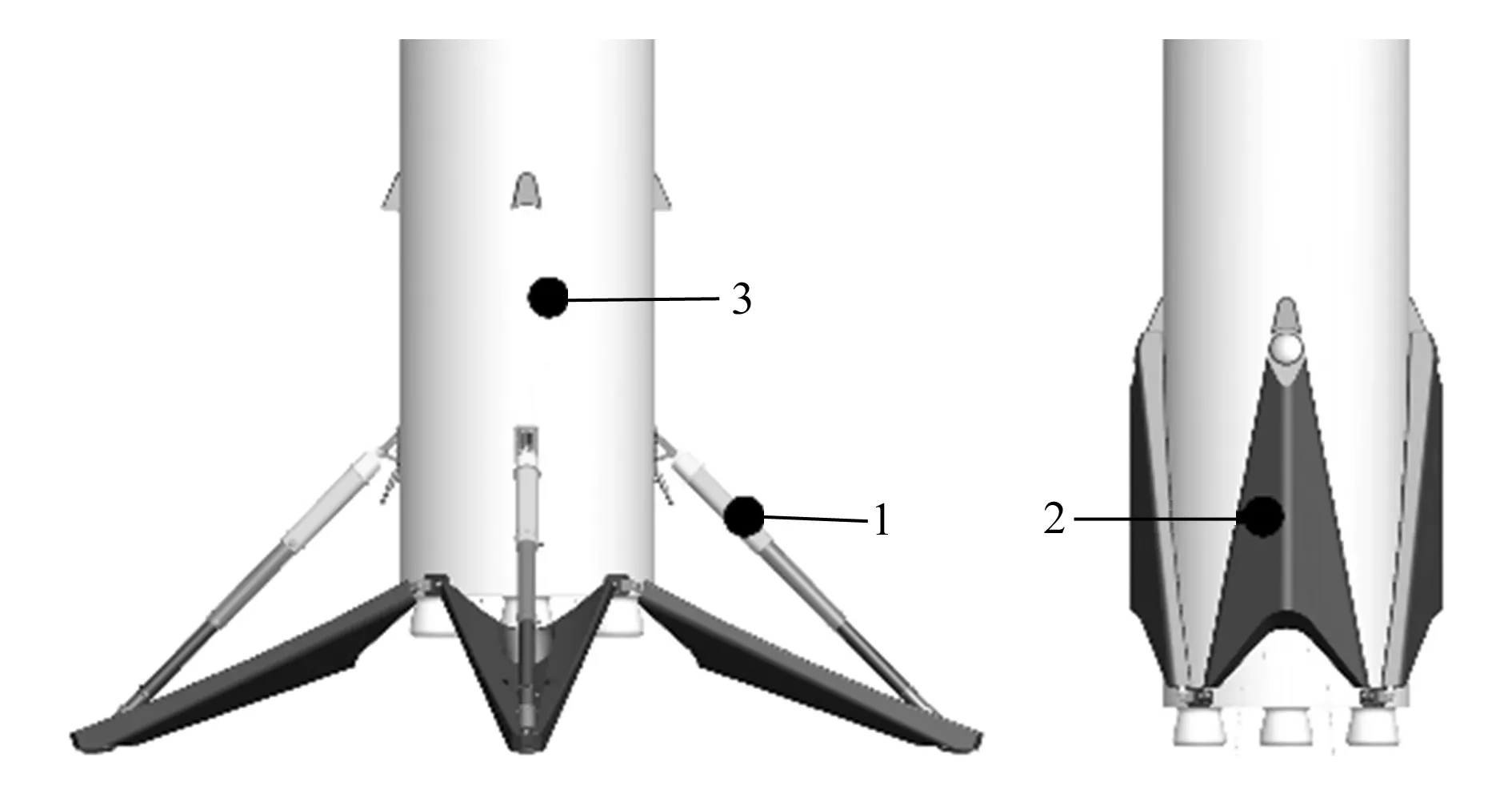
1—主着陆腿；2—副着陆腿；3—箭体

1.1 着陆支架运动学原理

着陆支架是一种典型的二维收放机构，通过主着陆腿的伸缩使着陆支架能够顺利完成展开与收拢。根据系统中各运动构件是否存在驱动力，将运动机构分为主动件和从动件。为了更加直观地明确着陆支架中各部件的运动参数，使用解析法中的矩阵法对着陆支架的运动原理进行分析，并作出以下假设：

1)主着陆腿是着陆支架收放过程中的主要旋转部件，是主动件；

2)将副着陆腿的投影等效地视为副着陆腿的运动机构。

由此，得到着陆支架运动机构的闭环矢量分析图，如图2所示。

图2 着陆支架运动机构的闭环矢量分析图

图中，Li(i=1,2,3)分别为主着陆腿、副着陆腿投影以及着陆支架上下支撑点间的X-Z平面内的矢量；li分别为主着陆腿、副着陆腿投影以及着陆支架上下支撑点间的长度；φi分别为主着陆腿、副着陆腿投影以及着陆支架上下支撑点间与Z轴正方向的夹角。

根据图2所示的矢量关系，可以得到闭环矢量方程为：

L1+L2+L3=0

(1)

Li(i=1,2,3)在X,Z轴上的投影代数之和f1,f2为0，可以表示为：

(2)

将式(2)对时间求导，可以得到着陆支架展开角速度与速度之间的关系：

(3)

着陆支架在运动过程中是否存在运动机构“死点”，可以由运动方程式(3)解的个数进行判断。若存在，则式(3)无解或有无穷多解。因此，当矩阵A的行列式为0时，可以得到：

(4)

由式(4)可知，当φ2=φ1时，存在着陆支架的运动机构“死点”。

1.2 着陆支架总体参数设计

基于着陆支架的运动学分析，采用拓扑方法，绘制着陆支架二维收放拓扑原理图。着陆支架二维收放拓扑原理图的正视图与俯视图分别如图3和图4所示。

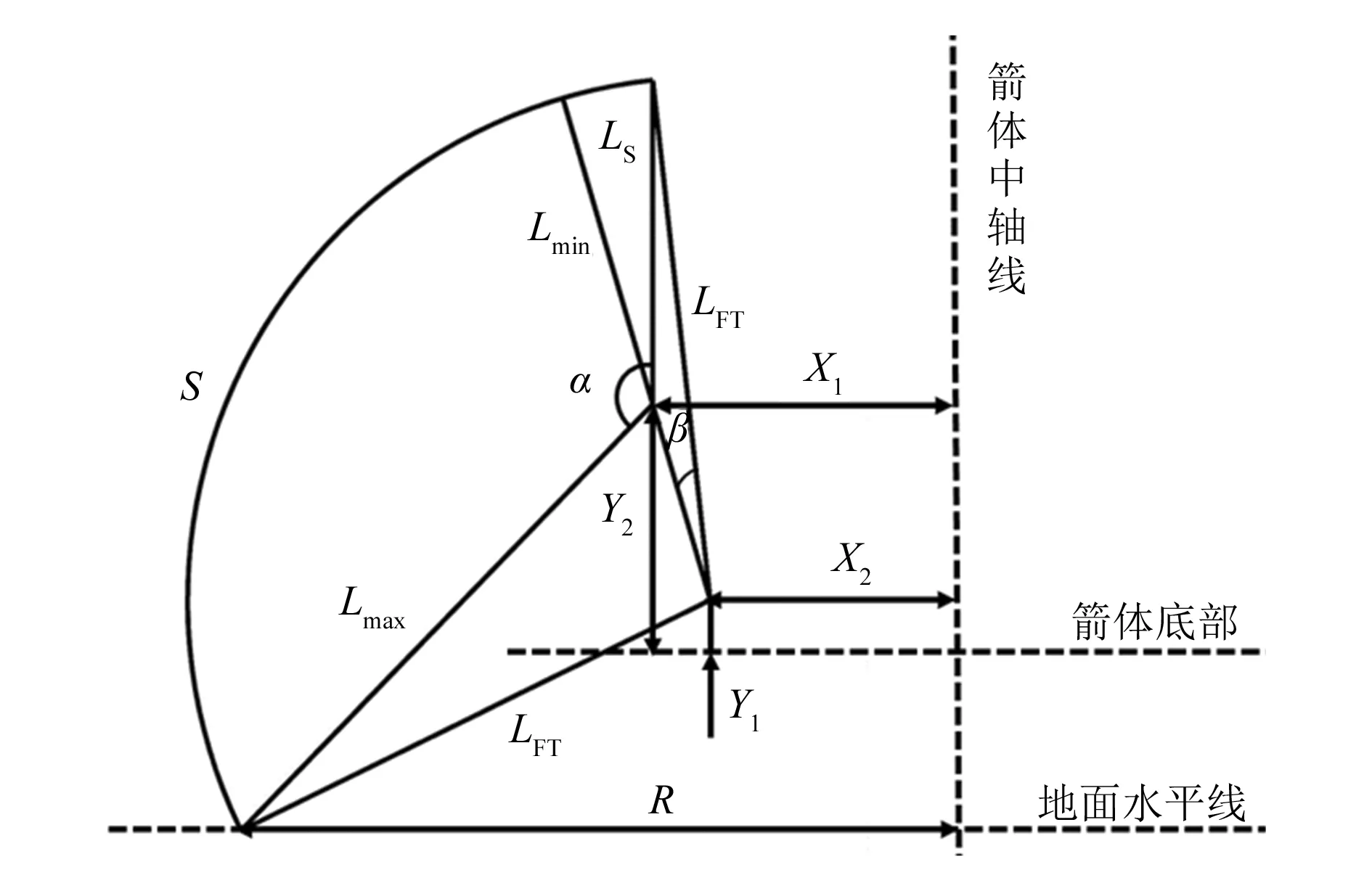
图3 着陆支架二维收放拓扑原理正视图

图3和图4中分别标出了着陆支架在运载器上的站位布局，主、副着陆腿的关键几何参数以及着陆支架展开过程中的关键角度参数等。

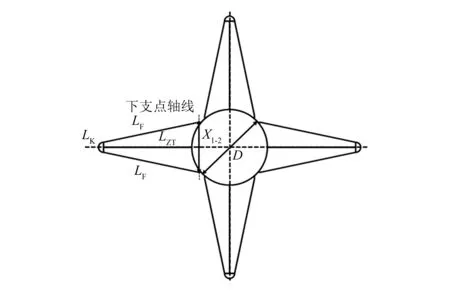
图4 着陆支架二维拓扑俯视图

着陆支架在运载器上的站位包括上支撑点到箭体中轴线的距离X1，上支撑点到箭体底部的距离Y1，下支撑点到箭体中轴线的距离X2，下支撑点到箭体底部的距离Y2，两个下支撑点的相对距离X1-2。

主、副着陆腿的关键几何参数包括主着陆腿的最大长度Lmax，主着陆腿的最小长度Lmin，主着陆腿的收起长度LS，主着陆腿的投影长度LZT，副着陆腿的长度LF，副着陆腿的投影长度LFT。

着陆支架展开过程中的关键角度参数包括着陆支架的最大展开角度α、着陆支架的“死点”角度β。

由总体设计要求可知：运载器箭体直径D为2 250 mm，着陆支架的最大展开角度α为135°，主着陆腿缓冲器最大行程为300 mm，着陆支架收起时纵向包络尺寸不大于4 000 mm，着陆支架的“死点”角度β不大于20°。通过迭代设计的方法，确定了着陆支架的总体参数，详见表1。

表1 着陆支架总体参数设计

2 着陆支架布局优化设计

着陆支架的布局设计会直接影响运载器着陆缓冲系统的综合性能，因此有必要在着陆支架的总体设计阶段对其布局进行优化设计。

2.1 数学模型的建立

鉴于运载器着陆工况种类多、数量大，选取运载器的4条着陆支腿同时着陆且无其他因素影响的典型工况，建立着陆支架的优化数学模型。基于对称性的原则，可以将受力进行简化，即只考虑着陆支架在X-Z平面内的受力。因此，所建立的优化数学模型如图5所示。

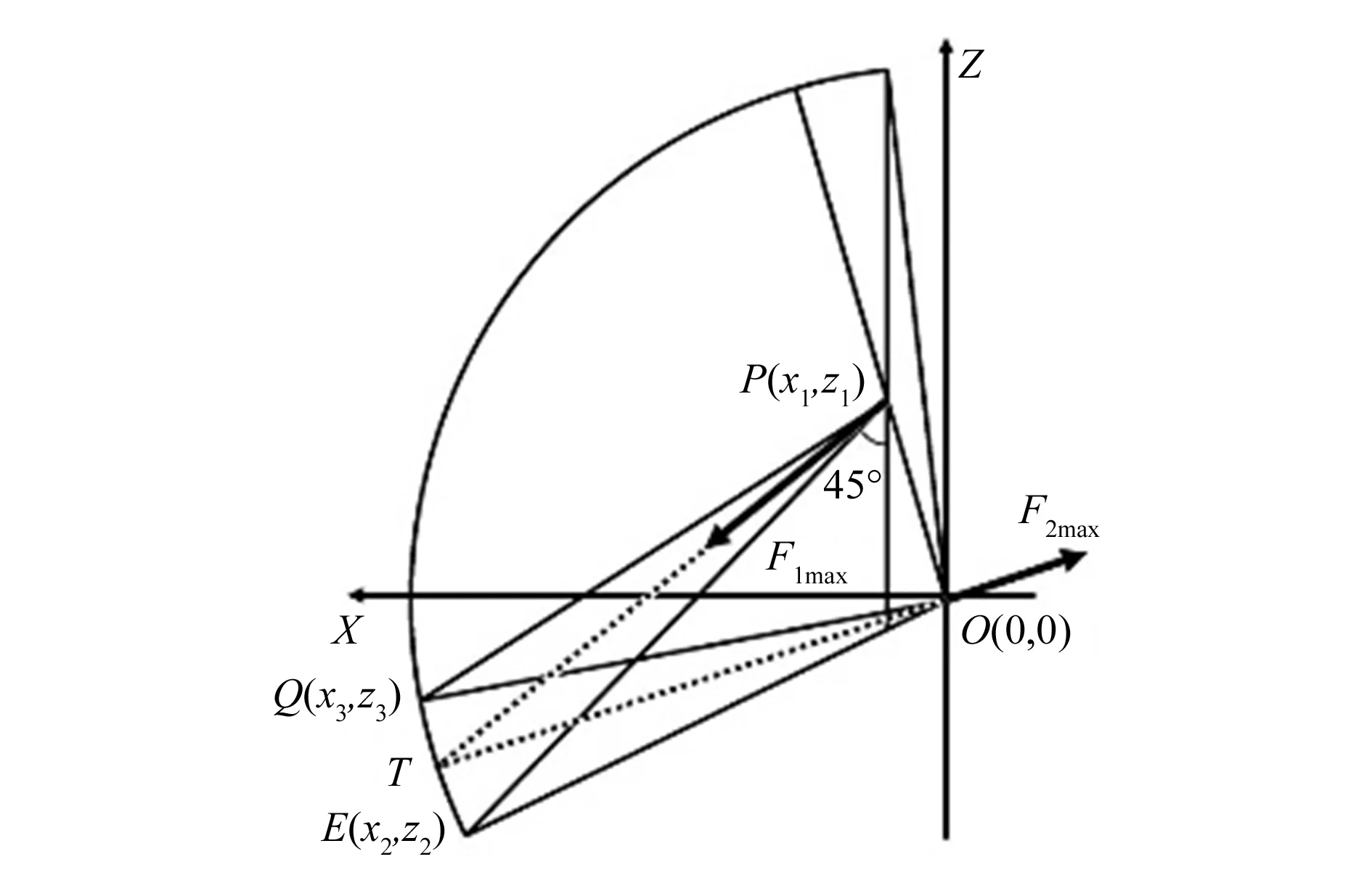
图5 着陆支架的优化数学模型

其中，坐标原点O为着陆支架的下支撑点在X-Z平面内的投影，P(x1,z1)为着陆支架的上支撑点在X-Z平面内的投影，E(x2,z2)为着陆支架完全展开时，主着陆腿与副着陆腿之间的铰结点在X-Z平面内的投影，Q(x3,z3)为缓冲器全压缩情况下主着陆腿与副着陆腿的铰结点在X-Z平面内的投影，PE为主着陆腿的最大长度Lmax，F1max为主着陆腿在着陆缓冲时受到的最大压力，F2max为副着陆腿着陆缓冲时受到的最大拉力在X-Z平面内的投影。根据几何关系可以得到以下关系式：

(5)

x2-x1=z1-z2

(6)

(7)

根据能量守恒定律可知，运载器着陆缓冲时的冲击能量是通过着陆支架中的缓冲器耗散的，即运载器着陆时的动能与缓冲过程中运载器势能改变量之和等于缓冲器内所做的功。因此得到如下关系式：

(8)

式中：s为缓冲器的最大压缩行程；η为缓冲器的工作缓冲效率，可以保守地认为η=60%；m为运载器的质量，m=5 200 kg；v为运载器着陆时的下沉速度，v=2 m/s；g为重力加速度，g=9.8 m/s2；h为运载器质心的下沉位移。将上述数据代入式(8)，则可将其改写为：

F1max=

(9)

根据图5所示的△OPT可以得到此时F2max与F1max之间的关系式：

(10)

根据上述分析，可以确定着陆支架具有4个独立的自变量和3个目标函数。4个自变量分别是着陆支架上支点P在X-Z平面内的横纵坐标x1,z1，着陆支架完全展开时主着陆腿与足垫之间的铰结点投影E的横坐标x2，缓冲器全压缩时，主着陆腿与足垫的铰结点投影Q的横坐标x3。3个目标函数分别是主着陆腿的最大长度Lmax，主着陆腿在着陆缓冲时受到的最大压力F1max，副着陆腿着陆缓冲时受到的最大拉力在X-Z平面内的投影F2max。

2.2 约束条件的确立

根据工程应用情况，着陆支架的站位布局设计主要受到其展开、收拢等功能约束，此外还应满足着陆稳定性、几何干涉、安全维护等要求，其安装位置更应该合理且易于操作。因此，根据图5所示的着陆支架优化数学模型，可以简化出主要约束条件为(单位：mm)：

1)着陆支架的上支撑点应满足机构的收放空间要求以及气动布局要求，即

250≤x1≤450

2)运动机构的“死点”角度不宜过大且整体布局合理，即

1 000≤z1≤2 000

3)着陆支架的展开半径应满足运载器的着陆稳定性要求，即

2 500≤x2≤4 000

4)为了保证着陆支架起到支撑、缓冲的作用，着陆支架的触地点应与运载器的尾端保持安全、可靠的距离(负号表示该参数位于图5 的第三象限，以下同)，即

-1 500≤z2≤-500

5)运载器在着陆缓冲时，着陆支架的水平位移应保证在合理的范围，即

100≤x3-x2≤200

6)保证运载器在转运以及安全维护等情况下，运载器上的尾端距地面有安全以及合理的距离，即

-800≤z3≤-500

7)在着陆缓冲时，主着陆腿的运动范围应处于缓冲器的行程之内，即

8)运载器在着陆缓冲时，着陆支架触地点应满足缓冲行程，即

x2≤x3

z2≤z3

2.3 计算方法的选择

着陆支架的布局优化问题是一个非线性的多目标优化问题。在众多的多目标优化算法中，快速非支配排序遗传算法(NSGA-Ⅱ)是应用最为广泛的一种算法。在MATLAB中，可以通过调用gamultiobj函数对着陆支架的布局优化问题进行求解，其算法流程如图6所示[5]。

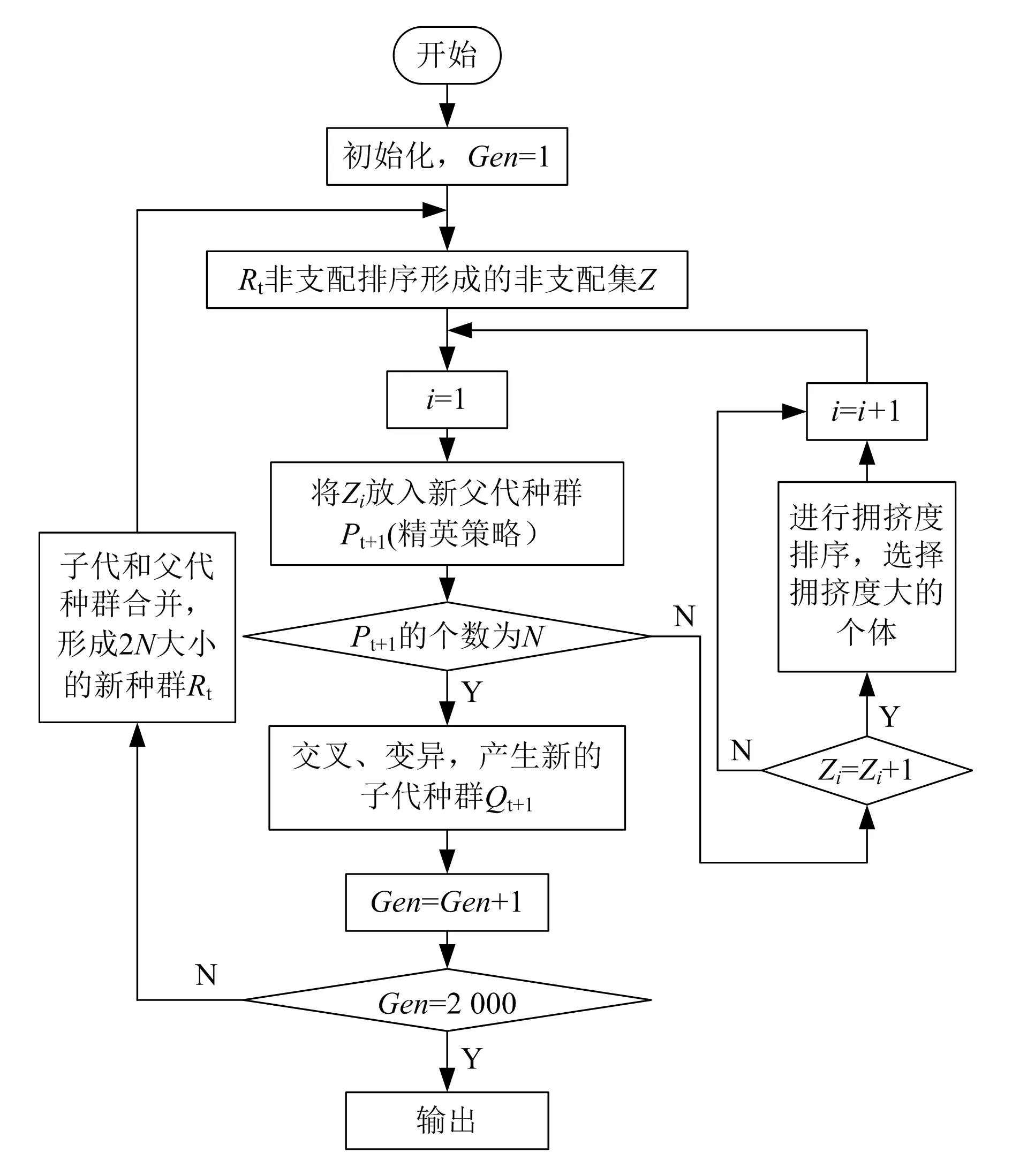
图6 gamultiobj函数算法流程

2.4 优化模型的求解

根据上述分析，可以将着陆支架总体布局的优化数学模型改写为：

X=(x1,z1,x2,x3)

在MATLAB中分别将目标函数以及非线性约束条件编写入两个m文件中，使用优化工具箱，选择多目标优化遗传算法gamultiobj函数，输入自变量的取值范围以及线性约束条件。同时，为了提高样本空间的数量以及种群的质量，将种群数量设置为2 000个，且在产生初始种群时选用自适应种群feasible population。通过调用目标函数和非线性约束条件的m文件进行求解计算，最终得到了50组非劣解集，从中挑选出符合实际情况的合理的最优解，其结果见表2。

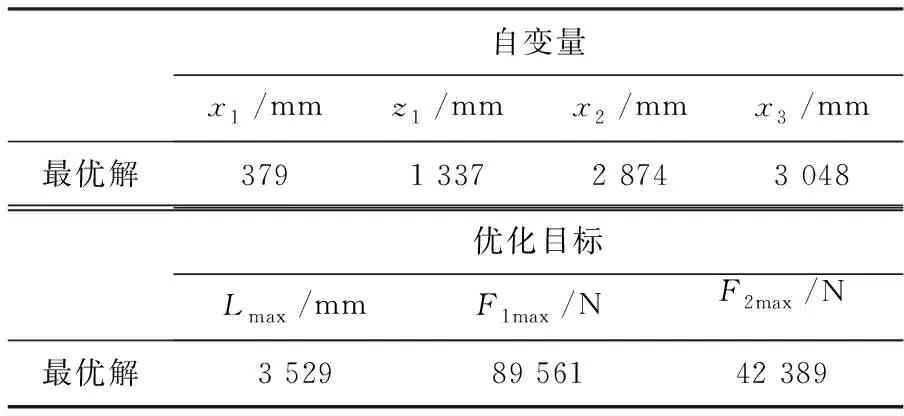
表2 总体布局设计参数最优解

为了明确优化前、后着陆支架在布局上的变化，对优化前后的设计参数以及性能参数进行对比，其结果见表3。

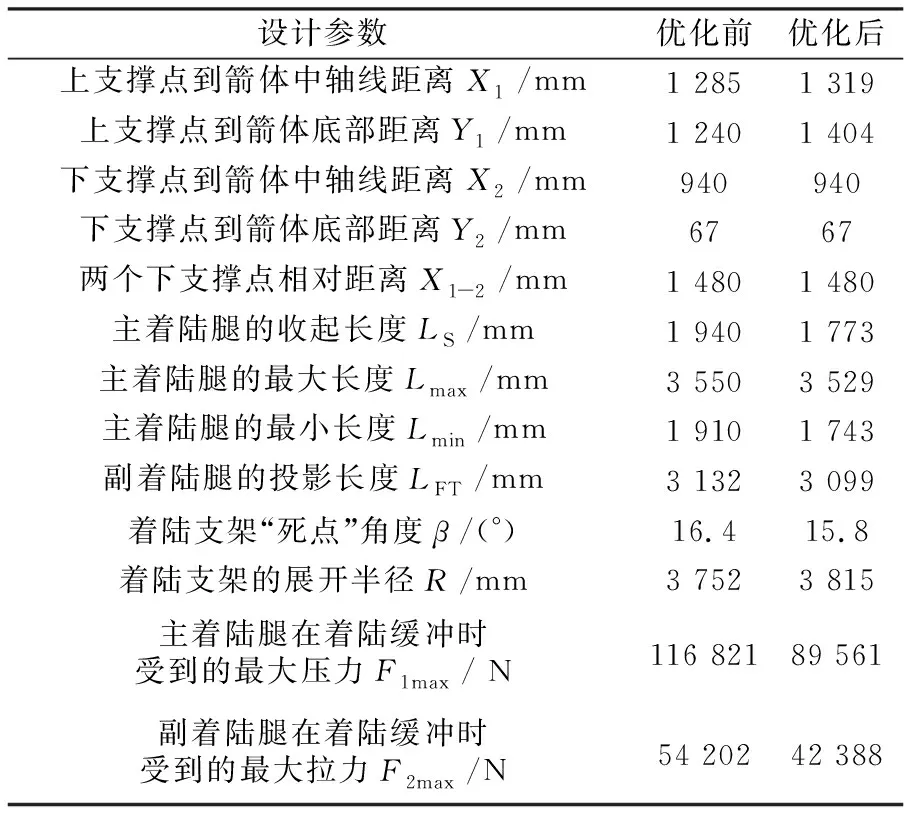
表3 优化前后的设计参数对比

由表3可知，在保证着陆支架展开角度以及下支点的相对位置相同的情况下，优化后的主着陆腿最大长度Lmax减小了21 mm，主着陆腿受到的最大压力F1max减小了约27 260 N，副着陆腿受到的最大拉力F2max减小了约11 814 N，有效地降低了着陆支架在着陆缓冲过程中的载荷。此外，上支点到箭体中轴线距离X1增加了34 mm，上支点到箭体底部距离Y1增加了164 mm，着陆支架“死点”角度β减小为15.84°，增加了主着陆腿的收放空间。与此同时，着陆支架的展开半径R增加了约63 mm。

3 动力学仿真分析对比

为了获得运载器在着陆缓冲过程中的动力学响应，依据着陆支架的总体设计方案，在动力学分析软件ADAMS/View中建立了参数化的着陆支架的动力学模型[6]。分别将优化前、后的设计参数输入到动力学模型中，对着陆支架的着陆动力学响应进行计算、分析，并将两组动力学模型中的冲击载荷、冲击过载与极限翻倒角关键参数进行对比。

在建立着陆支架的动力学模型时，仍需要考虑缓冲器的结构限制力、油液阻尼力、空气弹簧力和摩擦力等因素。在缓冲器的外筒与活塞杆之间需要添加油液阻尼力、空气弹簧力以及内部的摩擦力，其大小及方向可以由ADAMS内部调用函数进行定义。此外，还需要在外筒内部的底部与活塞杆之间建立刚性接触，接触刚度设置为无穷大，从而模拟缓冲器内部的结构限制力。在正常的着陆工况下通过控制等手段使运载器降落在指定的区域内，一般来讲指定区域内的着陆场地地面情况好、倾斜度小且地面不易沉陷，因此采用基于经典的赫兹接触理论的等效弹簧阻尼模型，对足垫与地面的非线性碰撞问题进行实时监测与模拟[7]，最终建立的着陆支架动力学模型如图7所示。

图7 着陆支架动力学模型

图7中1为主着陆腿与运载器之间的结点，2和3分别为副着陆腿与运载器之间的结点，4为主着陆腿与副着陆腿之间的结点。

在ADAMS中选取3种典型工况对着陆支架的动力学模型进行动力学仿真分析，这3种典型工况是按照着陆腿着陆的先后顺序进行分类的，其分别为垂直着陆、1-2-1式着陆以及2-2式着陆。

以垂直着陆工况为例，将优化前、后的设计参数输入到动力学模型中，得到下沉速度为2 m/s时的关键结点载荷的对比，见表4。

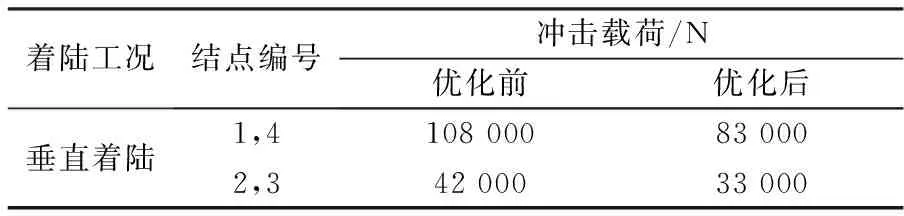
表4 关键结点载荷的对比

由于式(8)中并没有考虑摩擦力在运载器着陆缓冲时所做的功，因此在理论上使用式(9)和式(10)计算出的最大载荷比动力学仿真分析所计算出的载荷大。

通过改变着陆姿态偏差、着陆姿态角、着陆速度以及着陆高度偏差等着陆条件，分别进行仿真计算，并最终得到了着陆支架在3种典型极限工况下的着陆冲击过载与极限翻倒角等动力学响应，其结果对比见表5。

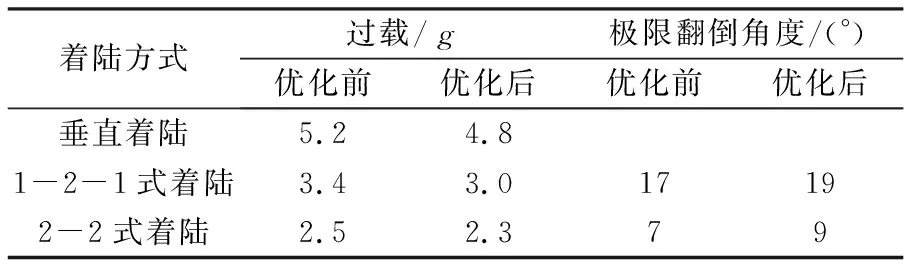
表5 着陆冲击过载与极限翻倒角的对比

由表5可以得出，3种典型工况下着陆支架在参数优化后其着陆冲击过载明显降低，极限翻倒角有所增大，从而使运载器的着陆稳定性得到了提高。

4 结论

本文提出了一种外翻式着陆支架的总体设计方案，在理论上分析了着陆支架的运动方式，揭示了外翻式着陆支架的工作原理。依据着陆支架的收放原理，建立其数学模型，使用MATLAB软件对其设计参数进行优化，并通过在ADAMS中建立的动力学模型进行对比、验证，所得到的结论如下：

1)着陆支架的总体参数设计主要取决于其在运载器上的站位、主着陆腿的最大长度和展开角度。

2)针对着陆支架的数学模型，通过多目标优化的方法，得到了着陆支架的最优设计参数与最优解。

3)参数优化后主着陆腿受到的最大压力以及副着陆腿受到的最大拉力分别降低了23.15%和21.43%，有效地降低了过载，提高了垂直起降运载器的着陆稳定性。