高速动车组制动模块结构可靠性分析及优化
2020-07-14田宗睿李永华唐玉珍吴永鑫
田宗睿,李永华,唐玉珍,吴永鑫
(1.大连交通大学机车车辆工程学院,辽宁 大连 116028) (2.大连交通大学研究生院,辽宁 大连 116028)
近年来,我国高速动车组研发技术愈发成熟,伴随着动车组产品的大规模使用,关键部件的可靠性与安全性逐渐成为研发人员关注的热点。在动车组的所有零部件中,制动模块无疑是最关键的部件之一。由于制动模块安装在动车组的车体下方,并且属于吊装部分,在动车组运行过程中制动模块会承担各种形式的载荷,从而会产生诸多的失效情况[1],因此很有必要考虑制动模块结构的强度和功能是否满足设计要求。
目前,针对制动模块的研究主要有静强度和疲劳强度分析、模态和谐响应分析、振动和冲击仿真以及模块化结构设计与方案改进。陈姝枚[1]利用静力学和动力学方法对地铁的制动模块进行强度和振动特性研究,并根据计算结果提出了改进方案。李成涛[2]对某动车组车下制动模块框架及螺栓进行的静强度非线性有限元分析,对其结构分析与改进具有重要意义。乔峰等[3]对制动模块总成局部断裂原因进行了分析,并提出了改进方案。袁海洋等[4]针对HXD3型机车制动模块提出了新的螺纹孔修复工艺。然而,上述学者的研究均忽略了结构可靠性对性能的影响,而且对制动模块进行结构优化的研究比较匮乏。有鉴于此,本文以可靠性为出发点,并结合尺寸优化基本理论,对优化后的结构进行可靠性分析,以便为制动模块的结构改进提供理论依据。
1 制动模块有限元分析
1.1 制动模块有限元模型建立
本文采用的制动模块主要由支撑架、风缸吊架、吊座、风缸、压力容器及水箱组成,其有限元模型如图1所示。
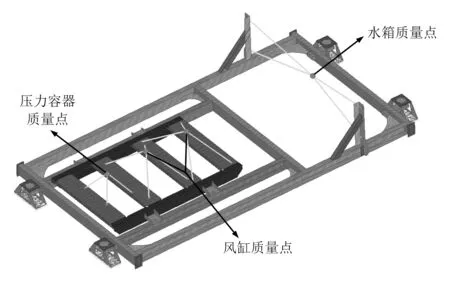
图1 制动模块有限元模型
该制动模块的制造材料主要为Q235,其材料属性见表1。

表1 制动模块的材料属性
根据铁道车辆规定的载荷要求,利用第四强度理论进行强度评估,动车组制动模块受力结构的静强度应该满足的条件如下:
1) 在正常载荷作用下,动车组制动模块所受的最大应力应不大于制造材料的许用应力。
2) 在最大载荷作用下,其所受的最大应力应不大于制造材料的屈服极限。
1.2 制动模块静强度分析
按照标准对动车组的制动模块分别建立横向、纵向和垂向的加速度工况。施加工况的具体数值见表2。

表2 静强度工况
注:g取值为9.81 m/s2。
利用ANSYS软件进行静强度分析。得到制动模块从第1工况至第3工况的Von.Mises应力云图如图2~图4所示。
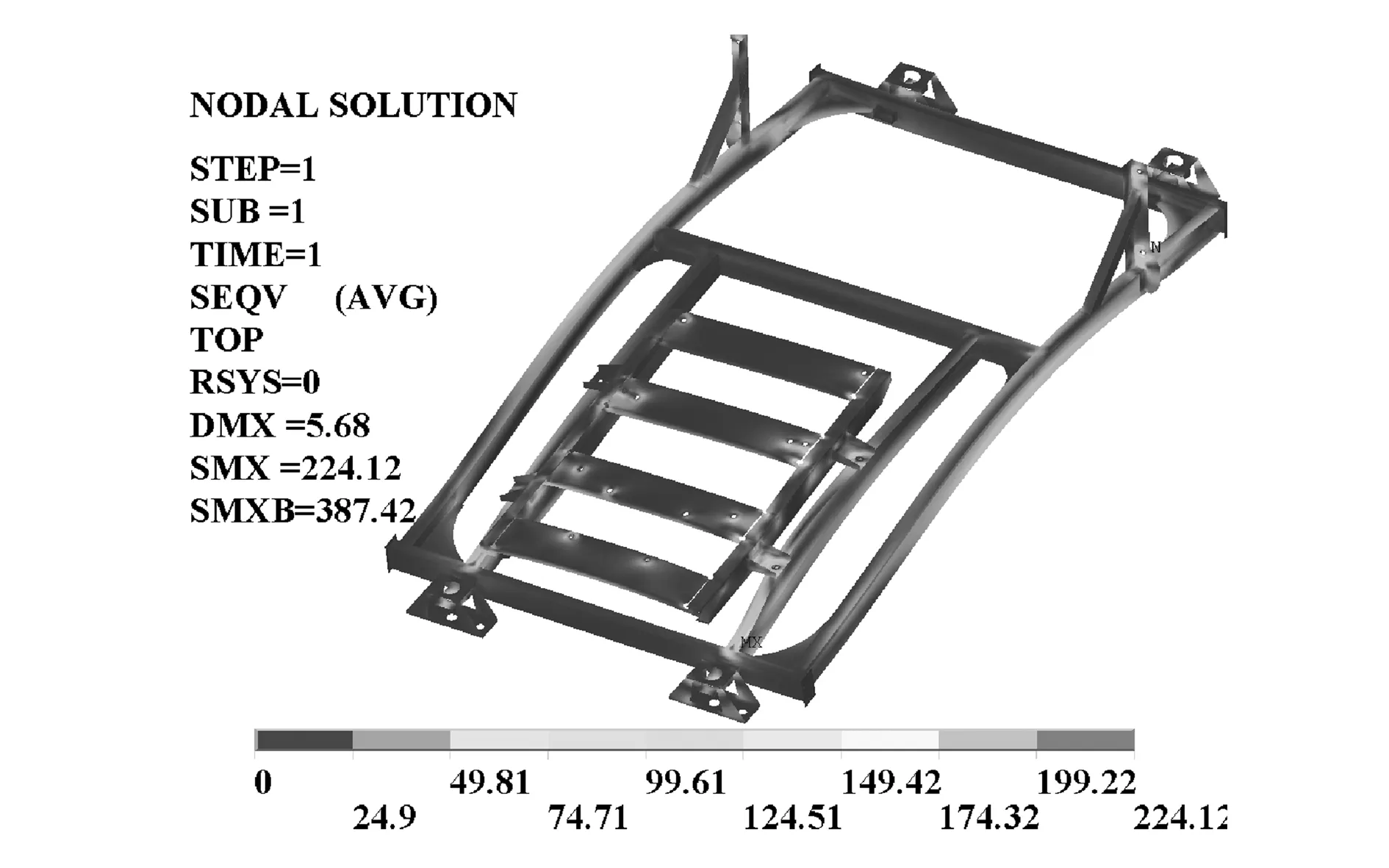
图2 第1工况Von.Mises应力云图
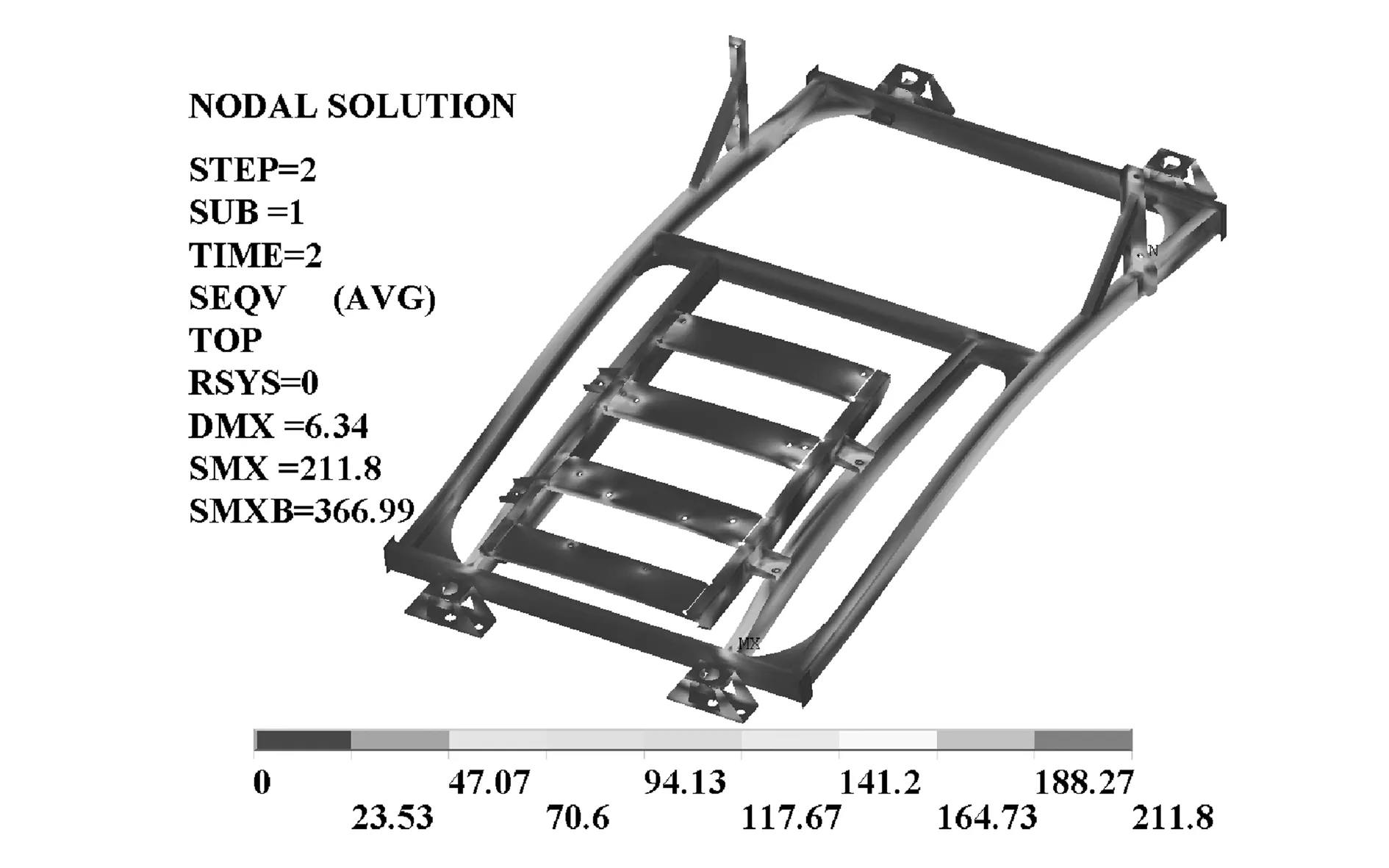
图3 第2工况Von.Mises应力云图
根据ANSYS静强度分析结果可知,3个工况的最大Von.Mises应力分别为224.12 MPa、211.80 MPa和181.60 MPa,均小于235 MPa,表明该制动模块强度符合使用要求。

图4 第3工况Von.Mises应力云图
2 制动模块结构可靠性分析
2.1 确定随机变量及可靠性分析方法
基于应力-强度干涉理论[5]建立制动模块的极限状态函数。令影响结构可靠性的n个变量为x=(x1,x2,…,xn),结构的极限状态函数为K=g(x),则制动模块的结构状态可表示为:

(1)
式中:R为强度,MPa;S为应力,MPa。
制动模块的可靠性分析在ANSYS软件中概率设计系统(possibility design system, PDS)模块[6-7]进行,在该模块中可利用响应面法[8]和蒙特卡洛法[9]进行可靠性分析。由于蒙特卡洛法中的拉丁超立方抽样具备不重复抽样的特性,可提高抽样效率,故选择此法进行可靠性分析。
令各随机变量服从正态分布,变异系数取0.05。选择不同位置的板厚作为随机输入变量,选择极限状态函数K作为输出变量。基本随机变量及其分布情况见表3。
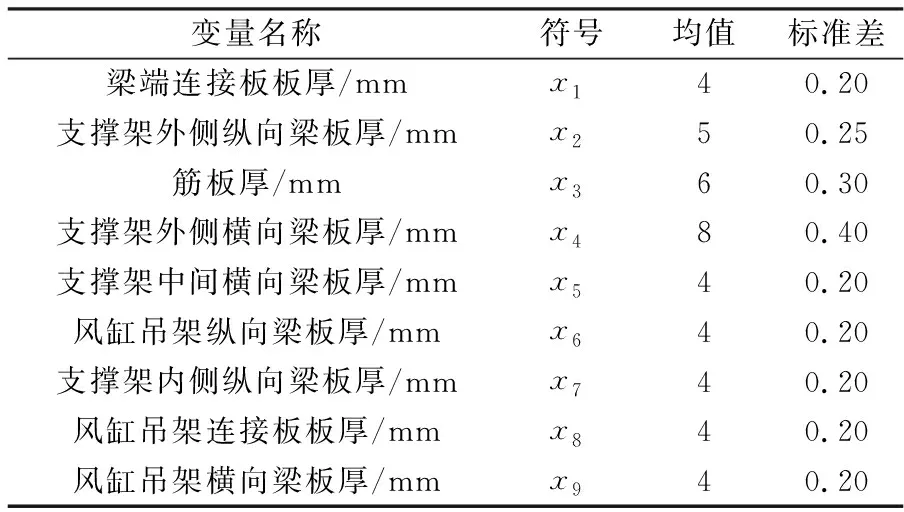
表3 基本随机变量及其分布情况
2.2 结构可靠性分析结果
根据静强度分析结果可知第1工况的最大Von.Mises应力(SEQV_MAX)最大,因此需要对第1工况下的制动模块进行可靠性分析。在后处理结果中可以得到样本历史曲线图、灵敏度图及可靠度结果。
1)最大Von.Mises应力的模拟精度。
样本历史曲线图能检验仿真模拟的精确程度,如果曲线能够趋于稳定,则表示模拟次数满足精度要求。在置信水平为95%时,最大Von.Mises应力的样本历史曲线如图5所示,置信水平表示样本点出现在置信区间的概率,上下两条曲线表示置信区间的上下限,其宽度能够准确反映模拟抽样次数[10]。
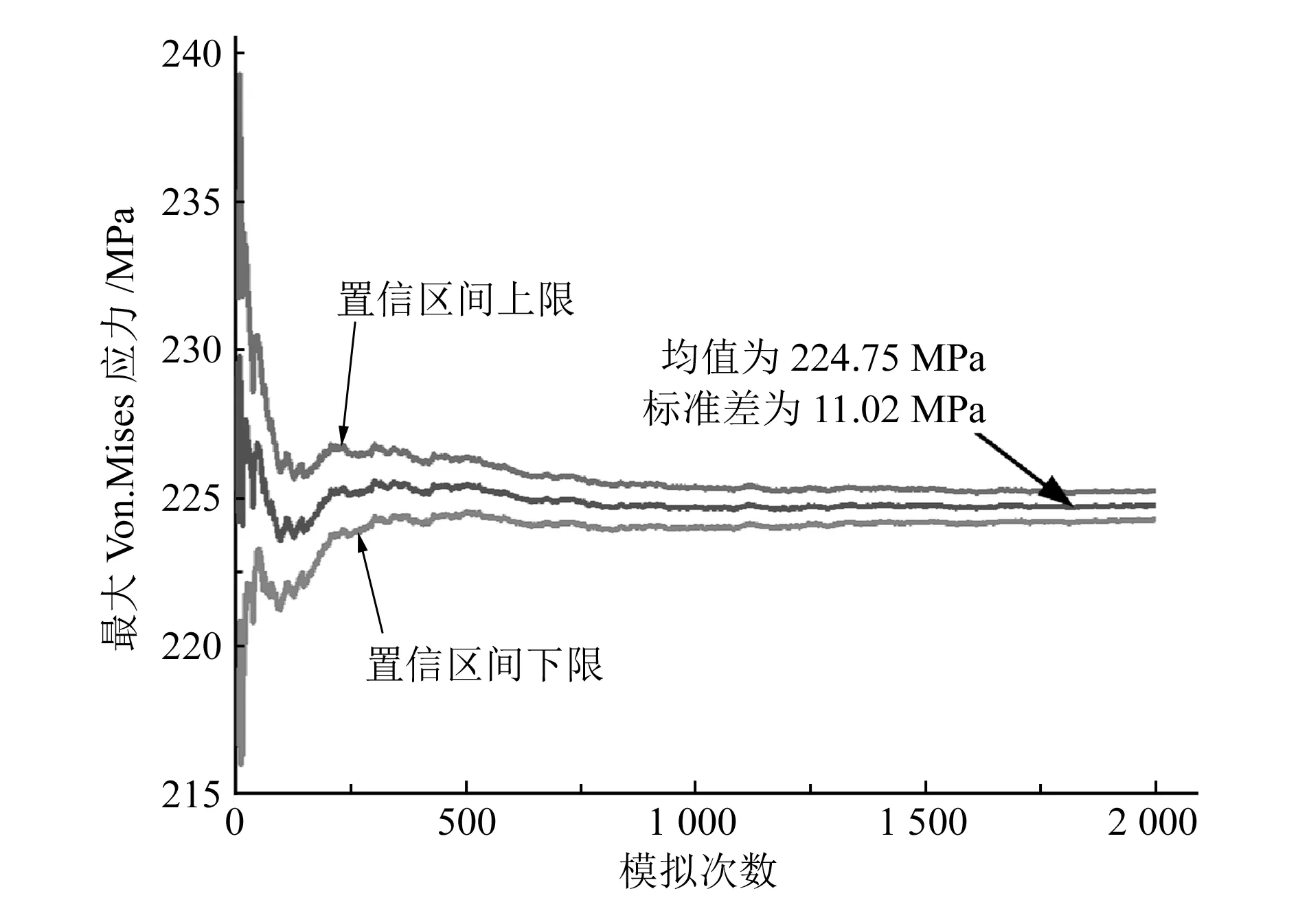
图5 最大Von.Mises应力样本历史曲线
由图5可知,2 000次蒙特卡洛模拟后,最大Von.Mises应力趋于稳定,逐渐接近一个固定值,表明该试验满足精度要求。最大Von.Mises应力的样本均值为224.75 MPa,标准差为11.02 MPa。
2)灵敏度分析。
灵敏度分析能够反映输出变量随各输入变量的变化情况。灵敏度主要说明所有的随机输入变量对输出变量影响的重要程度。此制动模块的随机输入变量对最大Von.Mises应力的灵敏度如图6所示。

图6 制动模块随机变量的灵敏度图
灵敏度图将各随机变量对最大Von.Mises应力的影响程度用百分率表示。由图6可知,在置信水平为95.000%时,支撑架内侧纵向梁板厚x7对最大Von.Mises应力的影响效果最大,灵敏度数值为0.982 3;筋板厚x3对最大Von.Mises应力的影响效果最小,灵敏度数值为0.004 4。x9,x4,x5,x1的灵敏度数值为正,说明这些参数变大时,最大Von.Mises应力的值随这些参数变大,呈正比关系。x7,x2,x8,x6,x3的灵敏度数值为负,说明这些参数变大时,最大Von.Mises应力会变小,呈反比关系。根据此分析结果,选择x7,x2,x9作为关键设计变量。
3)结构可靠度。
在置信水平为95.000%时,通过2 000次蒙特卡洛模拟,得到K大于0的概率结果如图7所示。
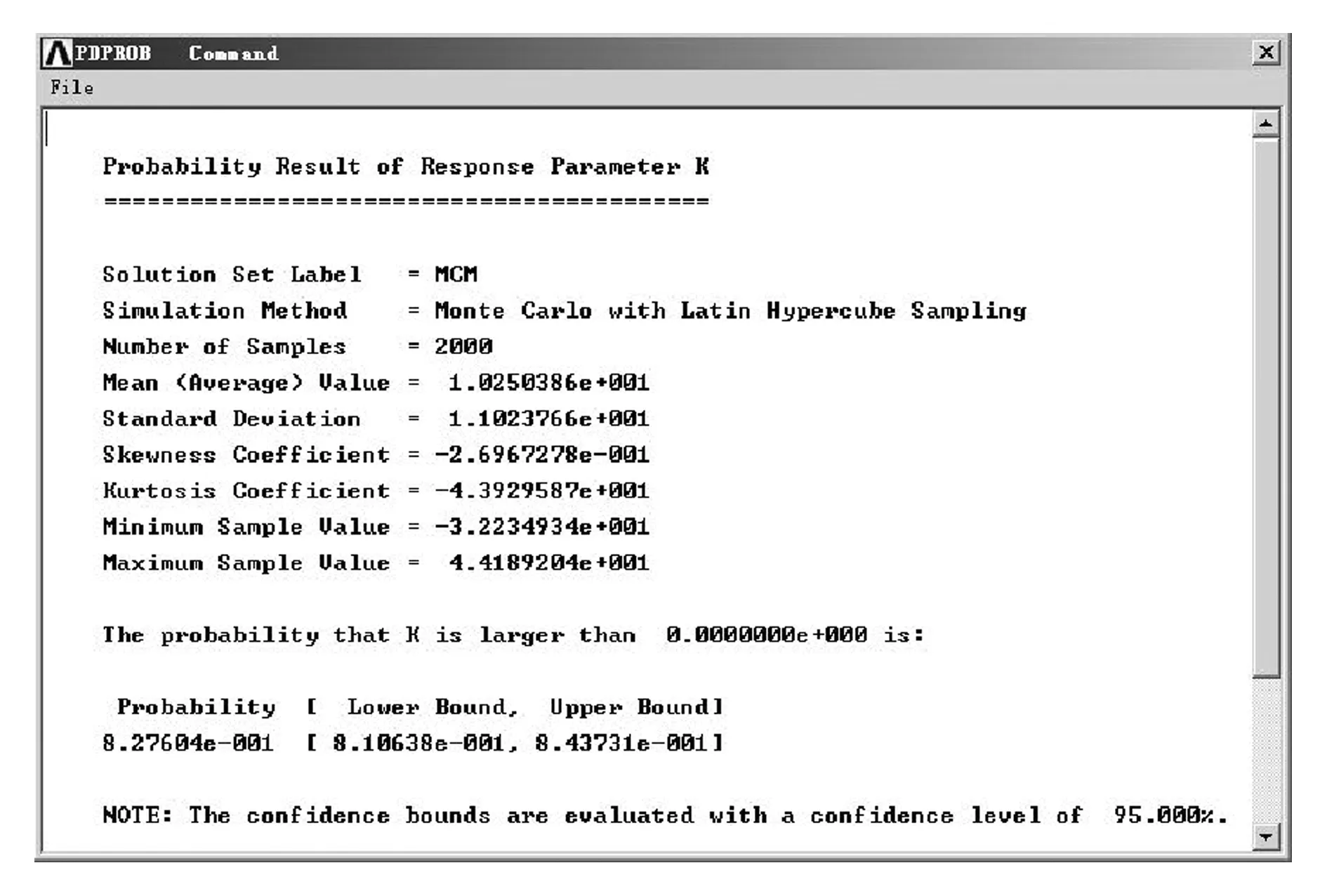
图7 K大于0的概率界面
由图7可知,在经过2 000次蒙特卡洛循环抽样后,极限状态函数K大于0的概率为82.76%,即动车组制动模块的结构可靠度为82.76%左右。
3 制动模块尺寸优化
根据静强度和可靠性分析结果,可知其可靠度与强度余量仍有提高空间,为提高动车组运行过程中制动模块的安全性与可靠性,需要优化制动模块结构。
前面的有限元建模、静强度分析、可靠性分析等步骤,主要研究对最大Von.Mises应力灵敏度较大的3个关键设计变量对最大Von.Mises应力的影响,设计其应力值达到最小的优化路径:利用ANSYS Workbench软件首先选择中心复合设计方法进行试验设计,再根据试验点选择方法拟合响应曲面,最后选择筛选法进行优化,并与优化前的分析结果进行对比,具体优化流程如图8所示。
3.1 建立优化数学模型
此优化中优化目标是求解最大Von.Mises应力的最小值。设计变量是3个板厚:支撑架外侧纵向梁板厚x2、支撑架内侧纵向梁板厚x7、风缸吊架横向梁板厚x9。约束条件是设计变量的上下限。
优化的数学模型表达式为:
minf(x)
s.t.xL≤xi≤xU,i=1,2,3
(2)
式中:xi为设计变量,mm;xL和xU分别为设计变量的下限和上限。

图8 优化流程图
3.2 响应面拟合
在Design Exploration模块中进行响应面拟合及优化。进行优化设计之前进行合理有效的优化设置是产生可靠结果的前提[11],优化设计变量取值范围见表4。

表4 优化设计变量设置 mm
由于中心复合设计(central composite design, CCD)计算一次或二次项效率更高,使用范围广泛,因此选择此法进行试验设计,进而根据试验设计点拟合响应面。因完全二阶多项式法理论简单、应用范围广,故采用此法进行拟合。其中,设计变量x2,x7对最大Von.Mises应力的响应面如图9所示。
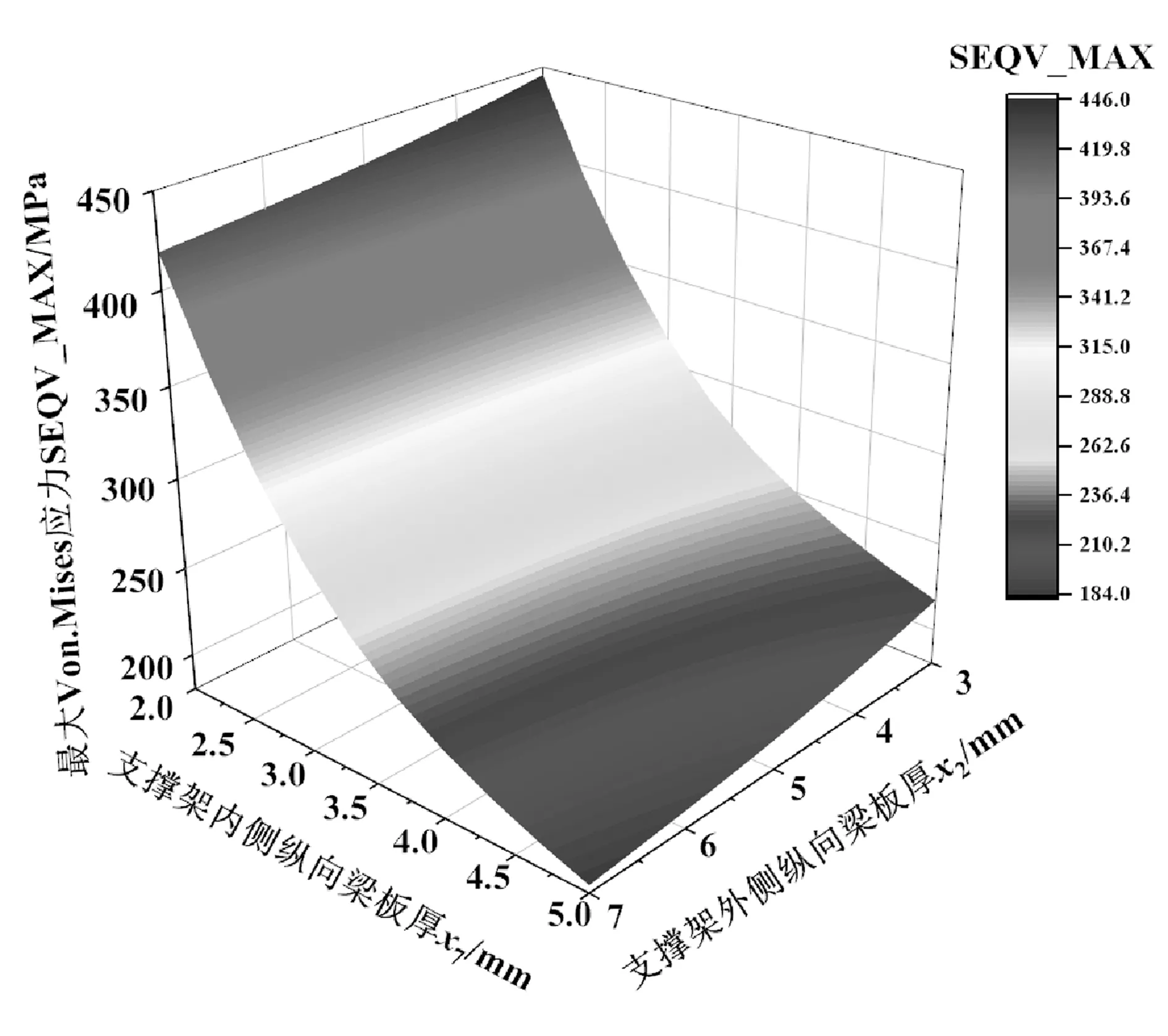
图9 x2,x7对最大Von.Mises应力的响应面
由图9可知,最大Von.Mises应力随着输入变量x2,x7的增加而减小。利用完全二阶多项式拟合响应面函数,得到最大Von.Mises应力表达式为:
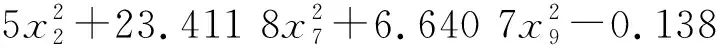
(3)
输出拟合优度的决定系数R2为0.998 5,其值接近1,表明拟合出的响应函数结果可信。
3.3 制动模块优化结果
在目标驱动优化模块中,选择Screening(筛选)优化方法[12],因优化精度与样本数有关,设置样本数为1 000以满足精度要求。
对优化后的结构进行静强度分析,得到的Von.Mises应力云图如图10所示。
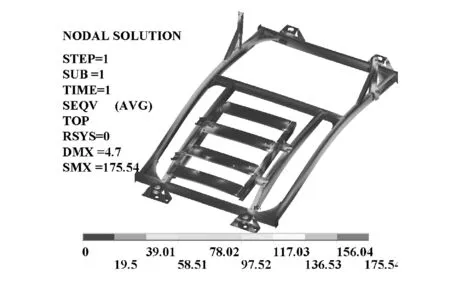
图10 优化后制动模块的Von.Mises应力云图
由图10可知,优化后最大Von.Mises应力值为175.54 MPa,小于Q235的许用应力,具有较大的应力余量,表明其强度满足要求。制动模块优化前后的各变量对比结果见表5。

表5 优化对比结果
通过对比结果发现,3个设计变量的数值均有所增加,最大Von.Mises应力数值明显减小,降低了21.68%。根据静强度的分析结果进一步分析得到的可靠度结果如图11所示。
进行2 000次蒙特卡洛法抽样后,制动模块可靠度达到100%,增加了17.24%,表明优化效果良好。
4 结论
1) 通过在ANSYS软件中对3个工况下的制动模块进行静强度分析得知,制动模块的最大Von.Mises应力均未超过材料的屈服强度,表明其静强度符合设计要求。

图11 优化后的可靠度界面
2) 根据静力分析结果,选取应力最大工况下的制动模块进行可靠性分析,得其可靠度为82.76%。通过灵敏度分析可知,支撑架内侧纵向梁板厚对可靠性影响最大。
3) 优化后,制动模块不但满足强度要求,并且可靠度提高了17.24%,表明该优化方案可明显提高制动模块结构性能,为制动模块的结构设计提供了新思路。
