基于Kf -μ-φ近似方程的深层叠前地震反演研究

王慧欣，张大海，张 纪，周静毅

（中国石油化工股份有限公司上海海洋油气分公司勘探开发研究院，上海 200120）

深部储层埋藏较深，入射角范围窄[1-4]（详见图1），速度高，而且物性差异小，反射特征不明显。常规流体因子比如Gassmann流体项受到诸多因素综合影响，增加了流体识别的难度，而Kf仅与流体的作用有关，有效地提升了流体识别的准确度。

图1是根据某实际工区特点建立的有关入射角随偏移距以及储层深度变化图，图中储层埋藏深度从0 m增加到7 000 m，速度从浅层1 600 m/ s增加到深层5 500 m/s，偏移距从0 m增加到4 000 m。通过该图可知：偏移距为4 000 m时，目的层深度为5 000 m时，则入射角最大值为30°左右，也就是在偏移距为某一固定数值时，入射角的最大值随着深度的增加而减小。

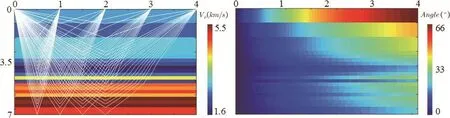
图1 最大入射角随深度变化

Yin X Y和印兴耀等分别在2014、2018年推导出基于Kf-fm-ρ-φ的四项和Kf-fm-ρ的三项AVO近似公式[5-17]，这两种方法在应用中都取得了较好的成果，但也同样存在一定的局限性。

对于Yin X Y等（2014）提出的Kf-fm-ρ-φ的四项AVO近似公式而言，它需要四个角度部分叠加道集；而且，该近似公式有四个反射系数，也就意味着反演的稳定性随之急剧降低。对于印兴耀等（2018）年提出的Kf-fm-ρ的三项AVO近似公式而言，首先，它将反射系数从四项降为三项，提升了反演的稳定性以及AVO近似公式的适用性，该公式可应用于入射角范围较窄的深部储层；除此之外，也降低了Kf-fm-ρ-φ的四项AVO近似公式中反射系数的相关性；但该方程需要以工区较为全面的岩石物理统计规律作为支撑，工作量比较 大。

本文基于Yin X Y等（2014）的Kf-fm-ρ-φ四项AVO近似方程以及Zhang等（2012）关于射线弹性阻抗的假设推导出了基于流体体积模量Kf、体积模量μ和孔隙度φ的三项AVO近似方程。

2 Kf -μ-φ近似方程推导

Yin X Y等（2014）推导出基于流体体积模量的Kf-fm-ρ-φ四项AVO近似方程：

式中：和分别是干、饱和岩石纵横波速度比的平方；Kf代表流体体积模量，N·m-2；fm=φμ代表固体刚性参数，N·m-2；μ代表体积模量，N·m-2；ρ代表密度，g·cm-3；φ代表孔隙度，小数。

本文在（1）基础上，根据Zhang F等（2012）的假设推导出基于流体体积模量Kf、体积模量μ

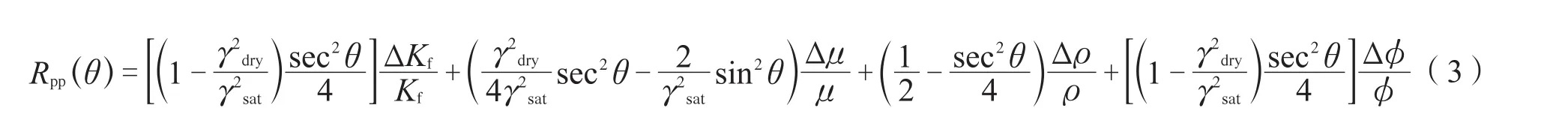
根据Zhang F等（2012）推导射线弹性阻抗时应用的假设：

式中：γ是横波速度反射系数与密度反射系数之间的拟合系数。将式（4）带入剪切模量的速度和密度的等式关系中：

对（4）式进一步推导，得到体积模量反射系和孔隙度φ的三项AVO近似方程。根据fm的关系式得到：

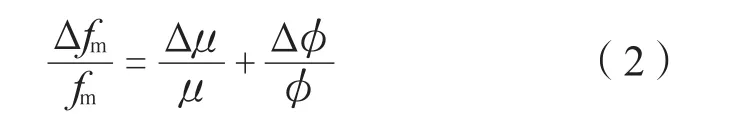
将（1）可改写为：

数和密度反射系数之间的关系：

将公式（5）带入公式（3）可以得到基于流体体积模量Kf、体积模量μ和孔隙度φ的Kf-μ-φ的三项AVO近似方程，如下：

3 Kf -μ-φ近似方程反射系数分析

为了对本文推导的Kf-μ-φ近似方程进行精度检测，经过文献查找，选取了岩性参数（表1）深层砂岩模型。用Zoeppritz方程和Kf-μ-φ近似方程计算地层界面处的反射系数（图2a）、两个方程反射系数差值（图2b）。

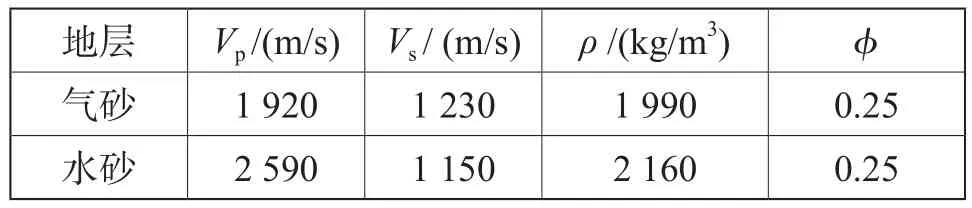
表1 深层砂岩模型参数

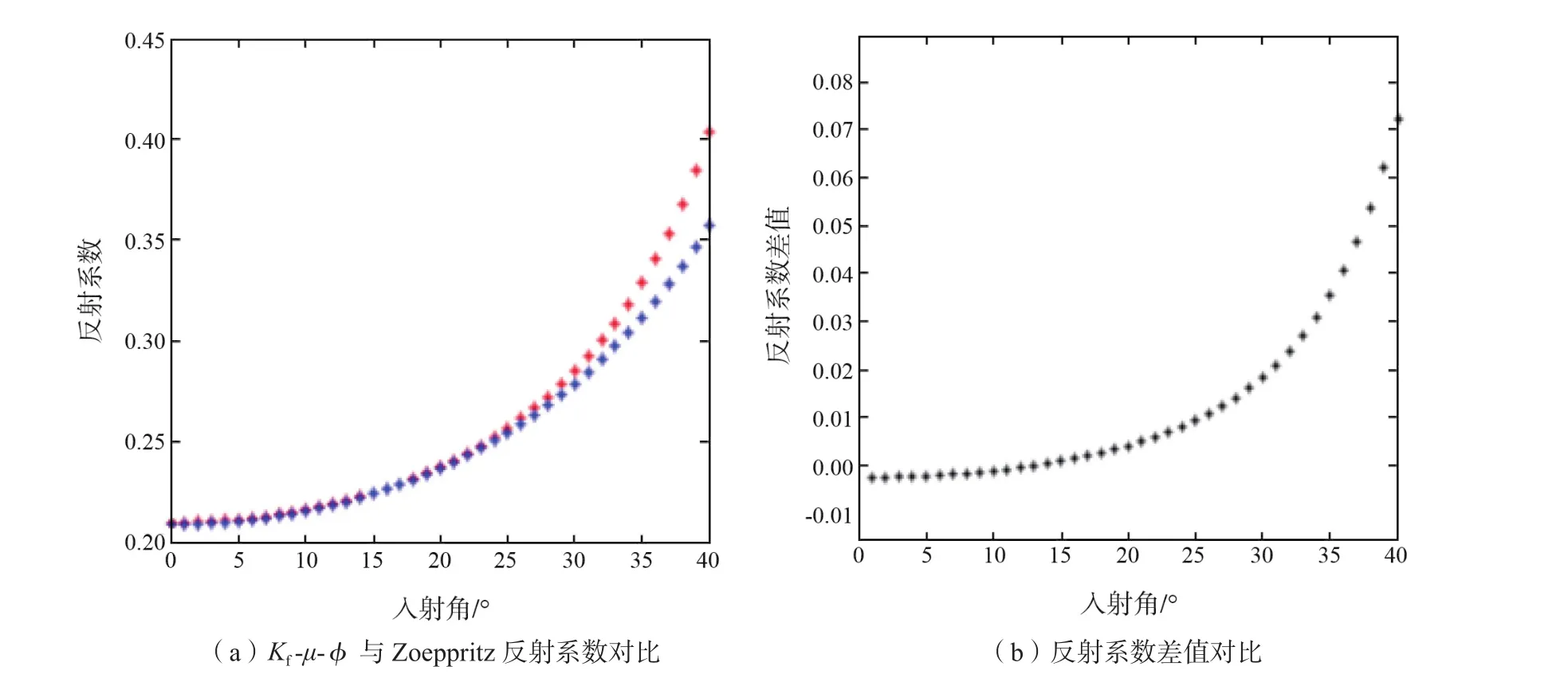
图2 深层含气砂岩模型反射系数对比

图2a是反射系数随入射角变化图，图2b是反射系数差值随入射角变化图。图2a中红色和蓝色分别代表由Zoeppritz和Kf-μ-φ近似方程计算得到的反射系数。入射角小于27°时，Kf-μ-φ近似方程与Zoeppritz方程的反射系数几乎没有差别，误差仅为0.015；入射角达到33°以上时，反射系数差值（图2b）明显增大。近似方程反射系数分析表明：Kf-μ-φ近似方程的精度满足了储层反演的要求。

4 Kf -μ-φ近似方程模型测试

首先利用测井曲线经过岩石物理计算得到的Kf、μ和φ曲线，根据Kf-μ-φ近似公式与30 Hz雷克子波褶积得到的叠前角道集，通过叠加得到用于叠前反演的小角度、中角度、大角度部分叠加道集，最后通过本文推导的三项AVO近似公式反演得到Kf、μ和φ曲线。

图3是无噪和SNR=2∶1两种情况下，原始的测井数据正演得到的0° ~ 30°的角度道集。图4为两种情况下通过叠前反演得到的Kf、μ和φ曲线（黑色：测井曲线，红色：反演得到的曲线）。在无噪情况下，Kf、μ的反演得到的数据与测井曲线几乎一致；当SNR=2∶1时，Kf的反演得到的曲线受到些许影响，在个别拐点略有偏差，整体趋势上，反演结果与原始井数据保持高度的一致性。整体而言，μ反演结果与Kf相比略差，原因是μ是由横波速度和密度得到的，实际测井数据中横波速度信息较为匮乏，而且密度项的相对变化较小；φ和Kf、μ相比其反演结果与原数据相比吻合度最差。经过分析原因有如下几点：一是由于φ的量级远小于Kf与μ，数据的变化幅度也不是十分明显；二是φ的反射系数与Kf和φ相比，其比重较小，致使φ项的反射系数信息量所占比重总体偏小，导致反演结果与原始曲线相比精确度较低，因而其反演结果并不能应用在实际工作中。模型试算从理论上证明了，通过本文方法进行叠前反演得到的流体体积模量数据与原始数据吻合度较高，同时抗噪性较好，因此该方法在理论上具有一定的可行性。

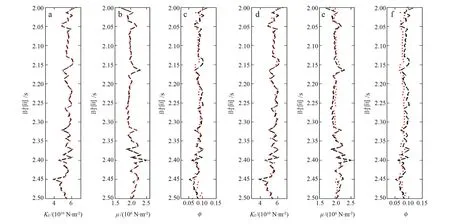
图4 无噪和SNR=2∶1情况下反演结果（黑色：测井曲线，红色虚线：反演数据）（a） （b） （c）无噪情况下反演结果；（d） （e） （f） SNR=2∶1情况下反演结果

5 实际资料应用

将本文提出的叠前反演方法在中国东部的某油田进行测试，其目的层埋藏较深，其物性较差而且入射角范围较窄。首先利用测井数据开展岩石物理交汇分析，寻找对工区目的储层最为敏感的流体因子。交汇分析对比发现：Kf作为流体因子，对于工区目的层最为敏感。如图5所示（上图为通过计算得到流体体积模量Kf和体积模量μ的井曲线，下图为流体积模量Kf和体积模量μ的交会图，红色代表目的层，蓝色代表干层，黑色代表其他），从图中可知：目的层的Kf数值明显小于干层，因此可以利用Kf将目的层区分出来。

利用本文提出的Kf-μ-φ三项AVO近似公式进行叠前反演，提取出流体因子Kf。由图6（利用本文方法通过反演得到的流体因子Kf剖面，图中插入的是测井曲线Kf）可知，Kf的反演结果与原始曲线吻合度较好，曲线Kf中偏小井段在反演结果中同样呈现偏小趋势，因而，本文提出的Kf-μ-φ三项AVO近似方程在实际应用中具有一定的可行性。

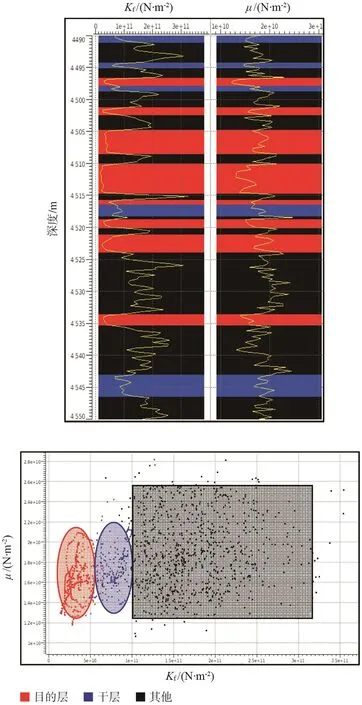
图5 测井数据（上）以及岩石物理交汇分析（下）图

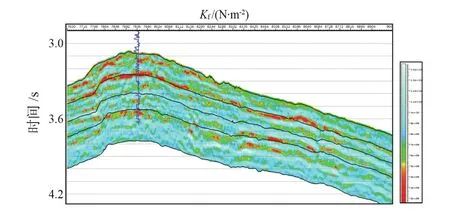
图6 流体体积模量反演剖面图

6 结论

本文根据推导出基于流体体积模量Kf、体积模量μ和孔隙度φ的三项AVO近似方程，该方程对岩石物理统计规律依赖性较小，更为稳定；在入射角小于27°时，反射系数与Zoeppritz方程的误差仅为0.015，精度满足反演的要求；同时，在无噪和有噪两种条件下，反演结果与原始测井曲线趋势一致，满足反演稳定性的要求；利用Kf-μ-φ方程反演是只需要三个角度部分叠加道集，反演的稳定性明显提升，且更加适用于入射角范围较窄的深部储层。

本文所提出Kf-μ-φ的三项AVO近似方程仍然存在一定的局限性：该公式包含孔隙度项，实际测井曲线中孔隙度信息匮乏，而且，其可靠性也远远低于密度和速度信息，因此，可能在反演过程中会导致一定的误差。