基于超级节点模型的框架结构地震反应分析
2020-07-14赵雯桐
赵雯桐,杨 红,李 戌,薛 茹
(1.郑州航空工业管理学院土木建筑学院,郑州 450046;2.重庆大学土木工程学院,重庆 400045;3.重庆大学山地城镇建设与新技术教育部重点实验室,重庆 400030;4.四川蓝光发展股份有限公司,重庆 401120)
钢筋混凝土梁柱组合体试验结果[1-4]表明,梁端纵筋屈服之前,贯穿节点区梁柱纵筋黏结滑移、节点核心区剪切变形对梁柱组合体加载端变形的贡献比较小,但梁端纵筋屈服后,上述两种节点非弹性变形成为梁柱组合体非弹性变形的较大组成部分。傅剑平[1]、吕西林等[4]的试验结果表明由梁筋滑移、节点剪切变形分别引起的梁端变形皆可达到梁端总变形量的30%~40%。徐云扉等[5]的框架结构低周反复试验结果表明梁筋滑移引起的梁端转角可达到梁端塑性铰区总转角量的35%。由于钢筋混凝土框架结构节点区应力状态复杂且非线性变形显著,中外学者已逐渐重视节点非弹性变形对框架结构非线性有限元分析结果影响的研究。
传统的节点非弹性变形模型化方法通常采用独立的单元分别模拟贯穿节点区纵筋滑移和节点剪切变形。Otani[6]在杆系模型中采用了在杆端设置考虑框架梁非线性弯曲变形的弹塑性转动弹簧P和考虑节点内梁纵筋黏结滑移的弹塑性转动弹簧S的方法,其中弹簧P采用基于修正Takeda模型的弯矩-当量转角恢复力关系描述框架梁的非弹性变形滞回规律,弹簧S采用基于双线性修正Clough滑移滞回模型的弯矩-当量转角关系描述纵筋滑移变形滞回规律,但该方法未考虑节点区剪切变形的影响。杨红等[7]基于该模型对平面框架考虑、不考虑梁纵筋滑移的强震非线性反应计算结果进行了对比,研究表明,节点内纵筋滑移未引起框架顶点位移时程反应较大变化,但会明显改变梁端塑性变形的组成方式。Banon等[8]提出在杆系模型中,除考虑构件非弹性弯曲变形的杆端弹塑性转动弹簧外,另在杆端附加一个综合考虑节点内纵筋黏结滑移和节点剪切变形的弹塑性转动弹簧,该转动弹簧的滞回规律由试验结果经回归分析得到。此模型的优点是能够较全面地模拟节点非弹性变形,但其采用的杆件弯曲变形与节点非弹性变形彼此独立的假定与实际情况不符,且无法考虑两种节点非弹性变形的比例变化。事实上,梁柱组合体试验结果表明[1-4],两种节点非弹性变形的滞变规律受轴压比、剪压比、混凝土强度、纵筋相对贯穿长度、配箍特征值等因素影响,其相对大小的关系较复杂。与上述方法类似,Alath等[9]利用一个转动弹簧,并在其周围连接一组刚臂模拟节点核心区剪切变形,其恢复力骨架曲线来自经验公式,刚度退化规律误差较大; Biddah等[10]采用两个黏结滑移弹簧单元和一个节点剪切弹簧单元分别模拟节点的纵筋黏结滑移、节点区的剪切变形。上述模拟方法力学模型简单、计算方便、有利于整体分析,但存在考虑因素不全面或恢复力模型误差较大的不足。
Elmorsi等[11]采用12个节点的平面应力单元模拟节点核心区,采用10个节点的过渡单元(共4个,其中梁、柱端各两个)模拟梁、柱端塑性铰,但未考虑纵筋滑移的影响。杨红等[12]基于对大量梁柱节点试验数据的统计分析,建立了综合考虑节点纵筋黏结滑移和节点剪切变形的材料模型,结合设置于梁端的零长度截面单元提出了模拟两种节点非弹性变形的方法,取得了较好模拟效果,但该模型是否适用于对柱端加载的梁柱组合体试验仍有待验证。
Laura等[13]提出了同时考虑节点内纵筋黏结滑移和节点剪切变形的“超级节点模型”。Mitra等[14]改进了其中的钢筋滑移模型,并通过大量试验校核了剪切分量的特征参数计算方法。超级节点模型具有力学模型精细、考虑因素全面、数值计算量适中的优点,受到研究者广泛关注,已引入OpenSees分析平台的梁柱节点单元(beam column joint element)之中。宋孟超[15]、解琳琳等[16]采用该模型对梁柱组合体低周反复试验进行了模拟,验证了其模拟结果较好;Shafaei等[17]采用超级节点模型对RC框架结构的弹塑性反应进行计算,但其分析对象侧重于节点设计有缺陷的框架,且未考察节点区的非线性变形特征。可见,现有研究一般采用梁柱组合体试验结果对超级节点模型进行对比、校核,将该模型用于整体结构非线性反应计算的研究成果较少,且缺乏节点反应规律的分析。
以钢筋混凝土平面框架结构为例,将采用超级节点模型建立的可考虑节点非弹性变形的框架有限元模型的强震反应与常规基于刚性节点的有限元模型的计算结果进行对比,考察节点非弹性变形对结构整体强震反应的影响,分析节点的非弹性反应特征及其对构件地震反应的影响。
1 超级节点单元模型
如图1[14]所示,超级节点单元包含13个分量,分别为8个钢筋滑移分量,用于模拟节点内梁、柱纵筋黏结滑移引起的节点强度、刚度退化;4个界面剪切分量,用于模拟节点四周交界面破坏引起的传递剪力能力的下降;1个剪切块分量用于模拟节点核心区剪切变形引起的节点强度、刚度下降。

图1 超级节点单元[14]Fig.1 The super joint element[14]

图2 一维荷载-变形滞回反应模型[18]Fig.2 The one-dimensional load-deformation response model[18]
在OpenSees中,基于超级节点模型建立的梁柱节点单元(beam column joint element)的滑移弹簧分量和剪切块分量均采用能反映加卸载刚度退化和强度退化的一维捏缩材料模型来描述其受力性能,如图2[18]所示;界面剪切分量可采用弹性材料本构模型。需注意的是,OpenSees中的滑移弹簧的黏结-滑移本构是基于传统单根钢筋拉拔试验建立的,并根据用户输入的混凝土抗压强度、钢筋材料特征(包括强度、弹性模量、直径、数量)、锚固长度和黏结强度由程序自动算出。
按照Mitra等[14]的建议,采用斜压杆模型确定剪切块分量的特征参数。
如图3[19]所示,斜压杆宽度取为
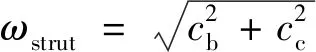
(1)
式(1)中:cb、cc分别为梁、柱截面受压区高度。

图3 斜压杆模型[19]Fig.3 The diagonal compression strut model[19]
斜压杆模型假定节点核心区的剪应力均匀分布且只通过斜压杆传递,根据力的平衡关系可以求得剪切块的剪应力为

(2)
式(2)中:fc_strut为斜压杆有效压应力;hb、hc分别为梁、柱截面高度;αstrut为斜压杆与梁轴线的夹角。
如图4[15]所示,核心区斜压杆的长度lstrut有如下关系:

(3)
斜压杆的压应变为

(4)
图4中θ为梁、柱截面的夹角,其初始值为90°,斜压杆受压总变形量为
Δstrut=Δstrut1+Δstrut2
(5)
式(5)中:Δstrut1、Δstrut2分别为斜压杆两端受压的变形量,剪切块剪应变为
γ=γb+γc
(6)
式(6)中:γb、γc分别为剪切块引起梁端和柱端的附加转角。据此可以确定节点剪切块的剪应力-剪应变关系。

图4 剪切块剪切变形[15]Fig.4 The shear deformation of shear panel[15]
2 平面框架基本信息及输入地震波
框架结构典型算例的抗震设防烈度为8度0.2g(g为重力加速度),抗震等级为二级,二类场地,设计地震分组为第1组。梁、柱和板均采用C30混凝土,梁、柱纵筋均采用HRB400级钢筋,梁、柱箍筋和板筋采用HPB300级钢筋,梁、柱保护层厚度均取为25 mm。
算例框架均按《混凝土结构设计规范》(GB 50010—2010)[20]和《建筑抗震设计规范》(GB 50011—2010)[21]设计,采用PKPM软件计算内力与配筋,其几何尺寸及配筋信息如图5(其中柱纵筋表示单侧配筋)所示。框架基本周期为0.802 4 s,最大层间位移角、周期比、位移比、剪重比、刚重比等均满足规范要求。
按照《建筑抗震设计规范》(GB 50011—2010)[21]的要求在美国太平洋地震研究中心(PEER)地面运动记录数据库中选取了7条地震波,各地震波的详细参数如表1所示,并对各地震波的地震动峰值加速度(peak ground acceleration,PGA)按8度0.2g的罕遇水准(4.00 m/s2)进行调幅。

图5 框架几何尺寸及配筋Fig.5 Dimensions and reinforcement of the frame

表1 各地震波的详细参数Table 1 The detail parameter of seismic waves
3 平面框架结构模型化方法
非线性分析均在OpenSees平台上完成。建立有限元模型时,梁、柱均采用基于柔度法的非线性梁柱单元(nonLinear beam-column element),分别在梁、柱单元内设置5个、4个积分点;截面对象采用纤维模型(fiber section);框架梁考虑左、右梁侧各6倍现浇板厚度的翼缘,形成T形截面。在此基础上分别建立了不考虑节点核心区非弹性变形的“刚性节点框架模型”、考虑节点核心区非弹性变形的“超级节点框架模型”,其中节点区非弹性变形采用梁柱节点单元(beam column joint element)模拟。上述两种框架结构有限元模型的唯一差别是,计算框架结构的强震非线性反应是否考虑节点非弹性变形的影响。由于OpenSees 中梁柱节点单元的功能、参数取值限制,“超级节点框架模型”只考虑中节点的非弹性变形,忽略边节点的非弹性变形。
两种模型的混凝土均采用OpenSees中Concrete01 Material,混凝土材料模型特征参数取值如表2所示;钢筋材料本构采用Steel02 Material,HRB400钢筋屈服强度按照平均值取为463.61 N/mm2,钢筋硬化率取为1%,其他钢筋材料参数采用OpenSees默认值。

表2 混凝土材料模型的参数取值Table 2 Parameter of concrete model
注:fc、εc分别为混凝土单轴受压峰值应力、峰值应变;fcu、εcu分别为混凝土的极限应力、极限压应变。
在“超级节点框架模型”中采用梁柱节点单元模拟节点非弹性变形时,梁、柱纵筋黏结滑移分量采用Bar Slip Material模拟,在输入混凝土抗压强度、纵筋屈服强度、纵筋弹性模量、纵筋直径、纵筋锚固长度等与纵筋滑移相关的参数后,程序自动计算得到钢筋应力-滑移骨架曲线,该算例框架部分节点的梁纵筋拉应力-滑移本构骨架曲线如图6所示。为便于观察钢筋屈服强度对应的滑移,图6中将程序计算的极限滑移值予以减小(但保持斜率不变)。

图6 梁纵向钢筋σ-s骨架曲线Fig.6 The skeleton curve of σ-s of longitudinal bar
剪切块分量采用一维捏缩材料模型模拟,该模型的8个特征点的参数取值需用户输入。根据如前所述斜压杆模型,通过编制MATLAB程序并计算,部分节点剪切块的剪应力-剪应变骨架曲线计算结果如图7所示。
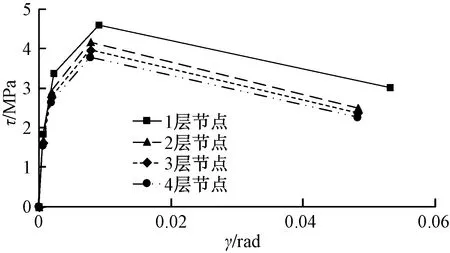
图7 剪切块剪应力-剪应变骨架曲线Fig.7 The skeleton curve of shear stress-strain of shear panel

图8 顶点位移时程曲线Fig.8 The top displacement time-history curves
4 框架非线性地震反应对比分析
4.1 整体反应
图8给出了GO2140、 NYA090和STN110三条地震波作用下两种有限元模型计算所得框架顶点水平位移时程曲线对比。结果表明,两种模型的计算结果在时程前期非常接近,在时程中、后期存在较小的差异。说明考虑节点非弹性变形对平面框架非线性分析的顶点位移时程影响较小。
表3所示为两种有限元模型计算的框架顶点位移最大值,其中括号内数值表示考虑节点非弹性变形的计算结果相对于“刚性节点框架模型”顶点位移最大值的减少百分率。由表3可见,“超级节点框架模型”分析得到的框架顶点位移最大值相对“刚性节点框架模型”多数略有减小、少数略有增大,可见节点非弹性变形对框架顶点位移最大值影响规律不统一,但影响程度不明显。
4.2 层间位移角
图9给出4条有代表性的地震波作用下的层间位移角分布,计算结果表明,考虑节点非弹性变形的层间位移角的大小、分布相对于“刚性节点框架模型”均有不同。在地震波B-ICC000作用下,“刚性节点框架模型”的层间位移角为0.020 8(略大于限值1/50),“超级节点框架模型”的层间位移角则小于1/50,但最大层间位移角的楼层号发生了改变(H-EDA360波和H-CHI012波作用下有类似现象)。总体而言,“超级节点框架模型”在各条地震波作用下的最大层间位移角相对“刚性节点框架模型”有不同程度减小。
4.3 杆端塑性铰分布
在地震波H-EDA360、STN110、B-ICC000作用下,框架分别按两种有限元模型计算所得塑性铰分布如图10、图11、图12所示,图中空心圆圈表示单向出铰,实心圆圈表示双向出铰,圆圈旁标注的数字为该塑性铰的转角延性系数需求。
计算结果表明,考虑节点非弹性变形的“超级节点框架模型”的出铰率总体上有所减小,很多在“刚性节点框架模型”中延性需求较小的杆端塑性铰在“超级节点框架模型”中不再出现,其主要原因是,考虑节点非弹性变形后,杆端部分非弹性弯曲变形转移到节点区,并引起较明显的节点区非弹性变形(具体详见后文);此外,结构的刚度变小、周期变大(“刚性节点框架模型”“超级节点框架模型”结构基本周期分别为0.996 4 s、1.036 3 s)可能引起地震输入减小。
需重视的是,虽然总体规律是在考虑节点区非弹性变形后梁端、柱端的转角延性需求减小,但仍有少量杆端在地震作用较大时,考虑节点区非弹性变形后杆端的转角延性需求会有所增大,如B-ICC000波作用下的第5层中柱上端、第4层中间跨梁端,H-EDA360波作用下的第3层边跨梁端等。出现上述现象的原因主要与地震动的随机性和结构在强震作用下非弹性反应的复杂性有关。

表3 顶点位移最大值Table 3 The maximum top point displacement
注:模型1指“刚性节点框架模型”;模型2指“超级节点框架模型”。

图9 层间位移角分布Fig.9 The distribution of inter-story drift ratio

图10 H-EDA360波作用下弯曲塑性铰分布Fig.10 Plastic hinge distributions under H-EDA360 wave

图11 STN110波作用下弯曲塑性铰分布Fig.11 Plastic hinge distributions under STN110 wave

图12 B-ICC000波作用下弯曲塑性铰分布Fig.12 Plastic hinge distributions under B-ICC000 wave

图13 B-ICC000波作用下“刚性节点框架模型”单元1弯矩-弯曲转角Fig.13 Bending moment-rotation angle of element 1 of “rigid joint frame model” under B-ICC000 wave

图14 B-ICC000波作用下“超级节点框架模型”单元1弯矩-弯曲转角Fig.14 Bending moment-rotation angle of element 1 of “super joint frame model” under B-ICC000 wave
4.4 杆端、节点滞回反应规律
图13、图14分别给出了两个算例框架在地震波B-ICC000作用下单元1 (第1层左侧边跨框架梁,见图5)端部截面的弯矩-弯曲转角(M-θ)滞回曲线。结果表明,考虑节点区非弹性变形后梁端弯曲转角变化规律与有限元模型有关,其中“超级节点框架模型”与中节点相连接的右梁端的弯曲转角明显减小,其原因是部分梁端非弹性弯曲变形转移到节点区,引起节点区出现较明显的非弹性变形(具体如图14所示),并导致图12中塑性铰数量减少、杆端延性需求下降;与边节点连接的左梁端的弯曲转角变化不明显,这是由于边节点未考虑核心区的非弹性变形。
由于B-ICC000波作用下框架的非线性反应最大(B-ICC000波作用下,“刚性节点框架模型”的最大层间位移角大于0.02,且梁、柱端塑性铰数量最多),故图15仅给出B-ICC000波作用下“超级节点框架模型”的单元36(第1层左侧中间节点,见图5)的剪切块滞回曲线和纵筋黏结滑移滞回曲线计算结果。图15表明,贯穿节点的梁纵筋滑移最大值很小(约0.3 mm),柱纵筋几乎没有滑移变形(柱纵筋未屈服);节点剪切变形也不大(不到0.008)。梁柱组合体试验结果[1-4]表明,对于配筋合理的梁柱节点,失效时梁筋在节点区的最大滑移量一般可达65~85 mm以上,节点核心区剪切变形则一般不低于0.022~0.045。可见,7条地震波作用下,按中国现行规范设计的8度0.2g区二级抗震框架一般不会出现节点剪切失效的破坏方式。
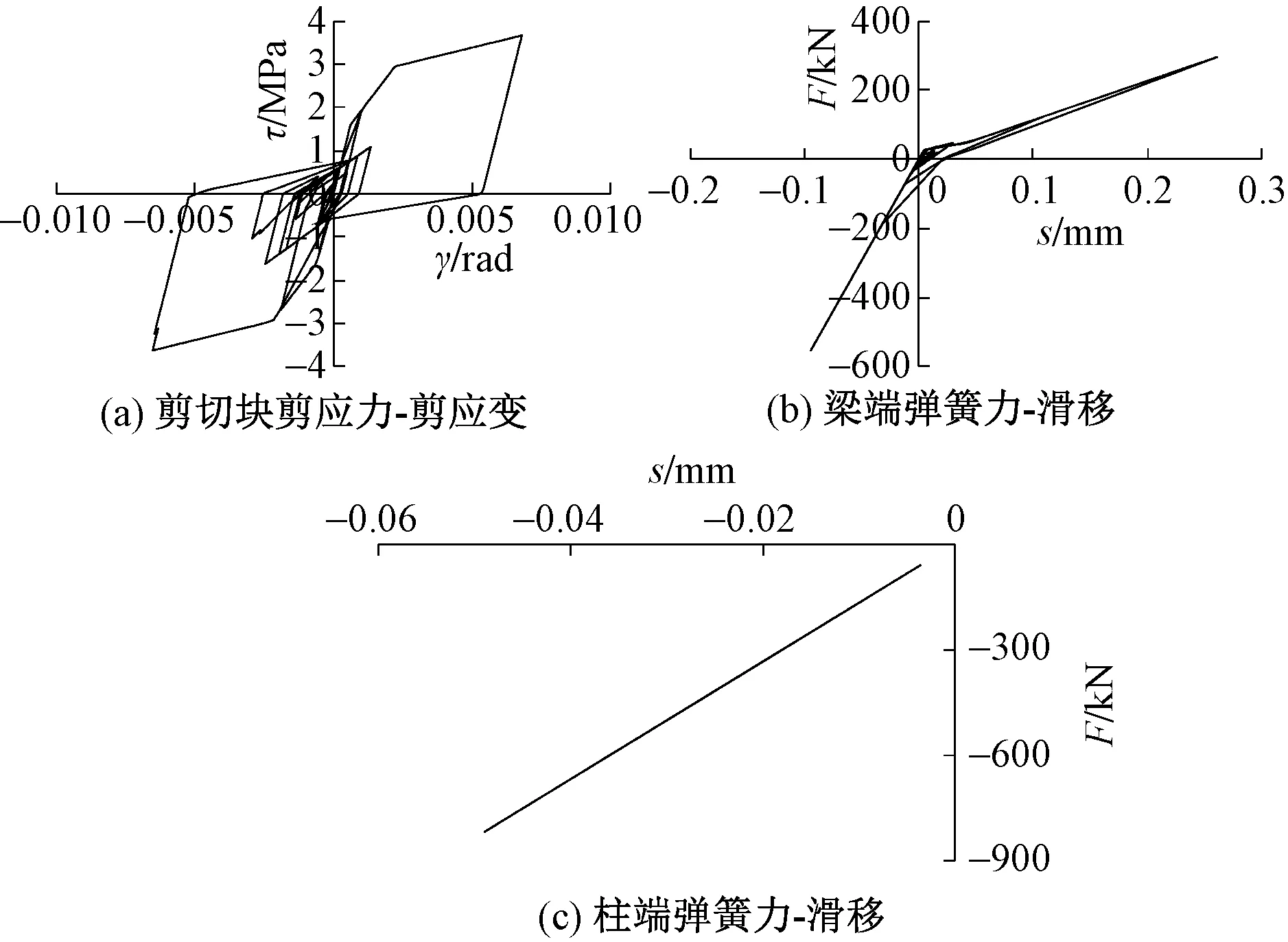
图15 B-ICC000波作用下“超级节点框架模型”单元36滞回曲线Fig.15 Hysteretic curve of element 36 for super joint model under B-ICC000 wave
5 结论
根据基于OpenSees的梁柱节点单元建立平面框架结构的非线性有限元分析模型,分析了节点非弹性变形对框架整体、局部非弹性地震反应的影响规律,得到结论如下。
(1)考虑节点非弹性变形影响后,框架顶点位移最大值变化不明显,层间位移角最大值略有减小。
(2)考虑节点非弹性反应时,框架杆端出铰率减小,梁端、柱端的转角延性系数总体上减小,其原因是考虑节点非弹性变形后,杆端部分非弹性弯曲变形转移到节点区,并引起节点区的非弹性变形。
(3)按中国现行规范设计的配置HRB400钢筋的8度0.2g区二级抗震框架结构,地震反应较大时框架节点距离剪切失效仍有相当高的安全储备。
(4)上述节点非弹性变形对框架结构强震非线性反应的影响规律仍有待整体框架的试验验证。
