基于核独立元分析的非线性工业过程故障诊断
2020-07-14张瑞成
张瑞成,裴 然
(华北理工大学电气工程学院,唐山 063210)
随着工业的快速发展,工业过程的复杂度越来越高,工业系统若发生故障会影响产品质量,甚至产生安全隐患。带钢热连轧过程是钢铁生产中的重要环节,它的工序复杂、设备量大,同时具有高速、高温、高压等特点,这就使得带钢热连轧过程是一个高故障率和危害性较大的生产过程[1-2],因此,能够快速准确地发现和找出故障可以保障生产过程稳定高效地运行。
传统的独立元分析[3](independent component analysis, ICA)只适用于线性过程,针对带钢热连轧过程连续、数据量大、过程复杂、各个变量之间具有较强的非线性关系的特点,可以采用核独立元分析[4](kernel independent component analysis,KICA)对工业过程进行故障监测。文献[5]将KICA方法引入非线性过程故障检测领域中,证明了此方法能够有效地抓住过程变量的非线性关系。当故障发生时会给出明显报警,一旦检测到故障,就有必要识别出故障变量。文献[6]在KICA方法基础上,利用支持向量机方法实现了轴承故障的检测与诊断。文献[7]提出了一种将堆叠稀疏自动编码器与KICA方法结合的复杂系统故障诊断方法。还有一种故障诊断方法是贡献图法,该方法由于不需要知道故障信息就可以进行故障诊断,目前得到了广泛的应用。文献[8]利用核函数梯度,推导出基于核主元分析诊断的贡献解析解,但机理不易理解。文献[9]提出了一种基于KICA方法的非线性贡献图法,并将其应用于非线性化工过程,验证了非线性贡献图法的有效性,但仅使用了传统的两个监控统计量。
针对上述问题,采用了一种基于超松弛因子改进的快速核独立元分析(Fast kernel independent component, FastKICA)和非线性贡献图法的过程监控与诊断方法。利用KICA对实际的非线性数据建立监控模型,通过在FastICA算法牛顿迭代过程中引入超松弛因子,放宽算法对初始权值的要求,从而建立监控统计量和控制限,检测故障信息。在检测到故障后,运用非线性贡献图法对故障变量进行诊断。最后以带钢热连轧过程为例,对基于改进KICA方法的非线性贡献图法进行仿真研究。
1 故障检测
1.1 基于超松弛因子的FastKICA方法
将正常工况的测量数据矩阵X=[x1,…,xN](N为数据的样本数量),应用非线性函数φ(·)将X映射到高维特征空间,得到Φ=[φ(x1),…,φ(xN)],则特征空间中的协方差矩阵为

(1)
函数φ(·)一般是未知的,通过核函数k(·)完成非线性变换,定义矩阵:
Kij=〈Φ(xi),Φ(xj)〉=k(xi,xj)
(2)

对数据Φ进行零均值化,核矩阵变为

(3)
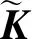

(4)
式(4)中:V=ΦHΛ-1/2=Φ[α1,…,αd]diag(λ1,…,λd)-1/2,H=[α1,…,αd],Λ=diag(λ1,…,λd)。


(5)
需要寻找一个混解矩阵W使得由下式估计的独立元特征向量S里的各个元素是相互独立的。
S=WX=BTZ
(6)
式(6)中:W=BTPT,B=[b1,b2,…,bN]为正交分离矩阵,即满足条件BBT=IN。
采用基于超松弛因子的FastICA算法[10],得到wk+1的迭代公式为
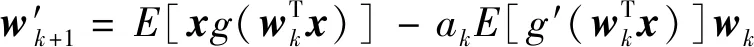
(7)

(8)
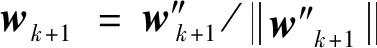
(9)

迭代后归一化和正交化w:
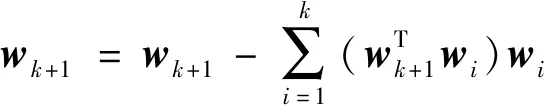
(10)

(11)
1.2 建立监测统计量
为了监控工业过程,需要计算以下3个监控统计量:

(12)

(13)
SPE(t)=e(t)Te(t)=[x(t)-

(14)
式中:t表示采样时刻:

2 故障诊断
2.1 非线性贡献图法故障诊断
对工业过程数据进行KICA分析,采用
和SPE监控统计量,可以对工业过程进行故障检测。一旦检测到有故障发生,就需要进一步对故障变量进行辨识。针对非线性KICA方法的故障检测,采用一种非线性贡献图方法用于故障变量的诊断。因此,过程变量对
和SPE监控统计量的贡献度可以定义如下:

(15)

(16)

(17)
对式(12)~式(14)进行进一步分析得:

(18)

(19)
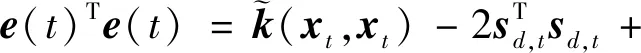
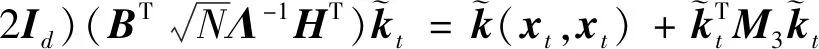
(20)
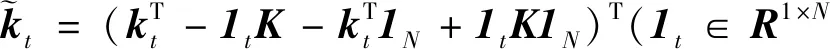
将式(18)代入式(15)得到:


(21)
同理可得:


(22)


(23)
2.2 故障诊断过程
基于超松弛因子改进的FastKICA方法的非线性贡献图法故障诊断步骤如下。
(1)根据式(1)~式(5),利用KICA方法获得白化矩阵Z。
(2)在高维空间使用基于超松弛因子改进的FastICA算法求得混解矩阵W。
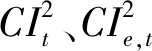
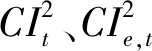

3 仿真与分析
3.1 带钢热连轧工业过程
图1描述了带钢热连轧(hot strip mill process,HSMP)的布局示意图。工业HSMP基本上由6个机组依次组成:加热炉、粗轧机、热输出辊道和飞剪、精轧机、层流冷却和卷取机[12]。粗轧过程中,热钢板的厚度大致减小,长度也随着厚度的减小而成比例增大。带钢通过转运台运输后,对带钢的头尾进行剪切,防止损坏工作辊。然后,作为HSMP的核心步骤,精轧机工艺(finishing mill process, FMP)给出了进一步和更精确的厚度缩减,以达到所需的精确厚度,这将作为本节的背景工艺。随后,极热带钢通过层流冷却设备(用水冷却),最终被盘绕成需要的产品。

图1 带钢热连轧机布置图Fig.1 Schematic layout of the hot strip mill
从图1中可以看出,精轧机组由7个机架组成,每组机架有4个辊,其中2个辊用于中间位置铣削,2个辊用于支撑外侧的工作辊。同时,每个机座都有自己的驱动装置,为工作辊提供主要的驱动力。通过快速液压执行机构定位备份辊,调整工作辊之间的间隙。出口厚度由X射线测厚装置测量,上游机架之间无法获得。仿真以某钢铁公司1 700 mm带钢热连轧生产线为研究背景,数据采用现场实测数据,其过程变量考虑为7个机架的辊缝、轧制力、弯辊力(第1机架无弯辊)共20个变量,质量变量考虑为精轧末机架的出口厚度。精轧机轧制过程变量及质量变量的分配如表1所示[13]。

表1 过程及质量变量分配Table 1 Assignment of process and quality variables
3.2 故障检测
引入的故障为精轧机轧制过程中第2、3机架间冷却水控制阀的执行器发生故障,当它不能按预设模式关闭时,会影响第3及之后机架的轧制力。而机架本身配有自动厚度控制器,因此辊缝会随轧制力的变化而变化,这会使得出口带钢厚度产生正向偏差,影响最终的产品质量,因此该故障为与质量相关的故障。在仿真中,选用2 000个正常工况下的实测数据作为参考数据,以及2 000个含有故障的实测数据作为采样数据,该故障从第5 s开始,持续10 s,在第15 s左右结束,采样间隔为10 ms。
利用线性ICA方法和非线性基于超松弛因子FastKICA方法对能够反映精轧机轧制过程的质量相关的采样数据进行检测,不同监控统计量的结果如图2~图6所示。
由图2、图3可以看出,ICA线性方法可以在故障数据样本点检测到故障的发生,但准确率不高,出现了很多漏报点,并且在无故障数据样本点有很多假报警现象;由图4~图6可以看出,基于改进的FastKICA非线性方法可以在故障数据样本点准确地检测到故障,仅在无故障样本点存在少量的假报警现象,大大提高了故障检测的准确率。

图2 基于ICA的T2统计量Fig.2 Statistical graph based on ICA of T2

图3 基于ICA的SPE统计量Fig.3 Statistical graph based on ICA of SPE
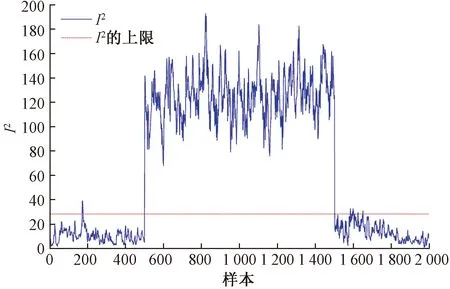
图4 基于改进FastKICA的I2统计量Fig.4 Statistical graph based on improved FastKICA of I2

图5 基于改进FastKICA的统计量Fig.5 Statistical graph based on improved FastKICA of

图6 基于改进FastKICA的SPE统计量Fig.6 Statistical graph based on improved FastKICA of SPE
3.3 故障诊断

图7 过程变量对T2的贡献图Fig.7 Contribution plot of process variables on T2


图8 过程变量对SPE的贡献图Fig.8 Contribution plot of process variables on SPE

图10 过程变量对的贡献图Fig.10 Contribution plot of process variables on

图11 过程变量对SPE的贡献图Fig.11 Contribution plot of process variables on SPE

4 结论
针对工业数据具有非线性特征,采用了一种基于改进KICA方法的故障监测和非线性贡献图的诊断方法,通过在带钢热连轧过程上的仿真研究,得出以下结论。
(1)基于超松弛因子改进的FastKICA非线性方法与传统的线性ICA方法相比,提高了故障检测的准确性,降低了故障假报警现象。
(2)基于非线性贡献图的诊断方法,解决了KICA 方法诊断领域存在的问题,克服了核函数引入的缺陷,实现了非线性过程下有效可靠的故障诊断。
目前,针对非线性工业过程的故障诊断方法研究还比较少,在今后的研究中会探索更多的适用于非线性故障诊断的方法。
