通道失配对GNSS阵列抗干扰性能的影响分析

陈飞强，鲁祖坤，陈 雷，李峥嵘，孙广富

(国防科技大学 电子科学学院， 湖南 长沙 410073)

全球导航卫星系统(Global Navigation Satellite System, GNSS)能为全球用户持续提供位置、导航和时间(Positioning, Navigation and Timing, PNT)等关键时空信息，已经在国防、电力、通信、测绘、智能交通等领域得到了广泛的应用。然而，GNSS的脆弱性仍是一个无法回避的问题，GNSS用户极易受到电磁干扰的影响。有研究表明[1]，辐射功率仅为1 W的干扰源即可使约15 km范围内的GNSS接收机无法正常工作。

在GNSS接收机层面，已有多种技术应对电磁干扰，包括时域抗干扰技术、频域抗干扰技术和空时(频)抗干扰技术等[2-7]，其中基于阵列接收机的空时(频)抗干扰技术被证明是目前最有效的抗干扰手段[8]。

阵列接收机由天线阵、多个射频通道以及数字处理芯片组成，射频通道由低噪放、混频器、滤波器等模拟器件组成。由于温度、环境差异及制造公差等因素的存在，阵列接收机的各阵列通道在实现时难以做到完全相同，不同通道间存在幅度和相位特性的不一致，即通道失配。

已有不少研究结果表明，通道失配会导致阵列接收机的抗干扰性能恶化[9-13]。但这些研究在评估通道失配的影响时，往往是在特定的信号干扰场景下进行的，即假设干扰和信号从某几个固定的方向入射。我们已经知道，阵列的抗干扰性能高度依赖于信号和干扰的入射方向，在某些特定场景下得到的评估结果可能不具有一般性，需要重新评估。另外，以往的研究通常以定性评估为主，缺少定量结果，难以达到指导工程应用的目的。

本文尝试按照统计性能评估方法的原则和思路，重新评估通道失配对阵列抗干扰性能的影响，并得到定量结果。

1 通道失配模型

通道的传输函数H(f)可表示为：

(1)

式中，f为频率，A(f)为幅频响应，φ(f)为相频响应，B为传输带宽。

理想的通道应当满足无失真传输条件，即在传输带宽内具有平坦的幅度和线性相位。理想通道的传输函数Hideal(f)可表示为：

(2)

式中，幅度A0为与频率无关的常数，τ0为通道的群时延。

实际的通道存在非理想特性，表现为幅度不平坦、相位非线性。对于阵列接收机，各通道的非理想特性也不一致，存在通道失配。文献[14]中提出了一种经典的通道失配模型，且被广为采用，在该模型中，阵列接收机第n个通道的传输函数Hn(f)可用下式表示：

(3)

图1 通道幅度失配模拟结果Fig.1 Simulation results of channel amplitude mismatch

图2 通道相位失配模拟结果Fig.2 Simulation result of channel phase mismatch

2 通道失配下的阵列抗干扰处理

为聚焦于通道失配的影响分析，假设天线阵元为理想各向同性天线，即不考虑各天线阵元方向图的差异及阵元间的互耦。不失一般性，考虑N元直线阵。假设远场处有一个期望信号(GNSS信号)和P个互不相干的干扰以平面波入射，到达角度分别为θ0和θk(k= 1,2,…,P)，则阵列接收信号矢量可表示为GNSS信号、干扰和噪声的叠加：

x(t)=s(t)+j(t)+n(t)

(4)

式中：x(t)为N维数据矢量，x(t)=[x1(t),x2(t)，…,xN(t)]T；n(t)为N维噪声矢量，n(t)=[n1(t),n2(t),…,nN(t)]T，这里假设噪声为高斯白噪声；a(θ0)为信号导向矢量，a(θk)(k= 1,2,…,P)为第k个干扰的导向矢量，导向矢量由信号(或干扰)的入射方向以及阵元相对参考接收点的位置坐标确定；s(t)为信号的复包络，jk(t)第k个干扰的复包络，hn(t)(n=1,2,…,N)为第n个阵列通道传输函数的冲击响应；上标“T”表示转置操作，符号“·”表示点乘，符号“*”表示卷积。

设空时滤波器的阶数为M，则滤波器的输入数据矢量(NM维)可表示为：

(5)

式中，Ts表示滤波器的抽头时延。

假设信号、干扰以及噪声之间不相关，输入数据矢量的自相关矩阵可表示为：

(6)

式中，Rss表示信号自相关矩阵，Rjj表示干扰自相关矩阵，Rnn表示噪声自相关矩阵，上标“H”表示共轭转置操作。经空时滤波器滤波处理后得到阵列输出信号为：

(7)

式中：上标“*”表示共轭操作；w为阵列权矢量，它是由空时滤波器的系数组成的NM维矢量

w=[w11，…,wN1，…,wN2，…,wNM]T

(8)

为获得阵列权矢量，在GNSS应用中通常采用不需要任何先验信息的功率倒置(Power Inversion, PI)算法[15]，其基本原理是以某一个阵元接收信号作为参考，调整空时滤波器的系数使阵列的输出信号功率最小。若以第一个阵元做参考，由PI算法确定的最优阵列权矢量可表示为：

(9)

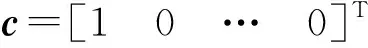
当阵列权矢量确定时，可以计算出阵列输出信干噪比，其定义为阵列输出信号功率与干扰加噪声功率之比，即：

(10)

阵列输出信干噪比可用来衡量阵列抗干扰处理后的信号质量。

3 基于统计性能的抗干扰性能评估

由于阵列抗干扰性能与信号及干扰的来波方向密切相关，不同的场景设置得到的评估结果往往差异较大甚至自相矛盾。为全面、准确评估通道失配对阵列抗干扰性能的影响，本文采用基于统计性能的评估方法[16]。

基于统计性能的评估方法基本思想是假定信号和干扰从各个方向随机入射，并采用蒙特卡洛方法估计各指标超过一定门限的概率。更具体地，本文采用信号可用率作为评估指标，其定义为阵列输出信干噪比超过一定门限的测试场景数占总的测试场景数的比例。

设蒙特卡洛实验的总次数为L0，阵列输出信干噪比门限为SINRTh，在L0次实验中，阵列输出信干噪比大于门限的次数为L1，则信号可用率P可表示为：

(11)

4 仿真实验

为了分析评估通道失配对阵列抗干扰性能的影响，用软件接收机进行仿真。首先用MATLAB生成阵列信号，用来模拟产生天线阵接收到的不同入射方向上的GNSS信号、干扰以及噪声。然后用通道失配模型对阵列信号进行处理，将通道失配的效应施加到阵列信号当中。最后用PI算法进行空时抗干扰处理，并统计各种通道失配参数下的信号可用率。基本的仿真参数设置如表1所示。

表1 仿真中用到的参数

下面分别从幅度失配、群时延波动和群时延偏差三个方面分析通道失配的影响。值得注意的是，下文中的失配参数均是结合了目前工程实现实际能达到的水平而设置的。

4.1 幅度失配的影响分析

图3给出了通道幅度失配对信号阵列抗干扰性能的影响，其中空时滤波器的阶数M设置为5。从图中可以看出，幅度失配对信号可用率影响较大。以阵列输出信干噪比损耗3 dB为门限(实际抗干扰测试中约定的门限，即抗干扰后的信噪比比输入信噪比低3 dB，在本实验中此门限值为-33 dB)，当幅度失配为0.3时，信号可用率由无失配时的67.6%降至37.3%；为使信号可用率下降不超过10%，应当使幅度失配小于0.15。

图3 通道幅度失配对阵列抗干扰性能的影响Fig.3 Effect of amplitude mismatch on the performance of antenna array

图4 幅度失配条件下空时滤波器阶数对信号可用率的影响Fig.4 Effect of number of filter taps on the performance of antenna array under amplitude mismatch

4.2 群时延波动的影响分析

图5 通道群时延波动对阵列抗干扰性能的影响Fig.5 Effect of group delay variation on the performance of antenna array

4.3 群时延偏差的影响分析

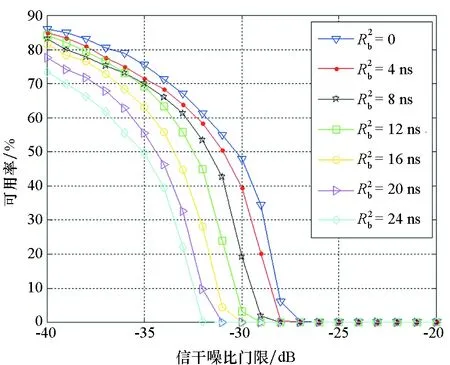
图6 通道群时延偏差对阵列抗干扰性能的影响Fig.6 Effect of group delay bias on the performance of antenna array

图7 群时延偏差条件下空时滤波器阶数对信号可用率的影响Fig.7 Effect of number of filter taps on the performance of antenna array under group delay bias

5 结论

本文分析评估了通道失配对GNSS阵列抗干扰性能的影响，区别于传统的基于特定场景的评估方法，本文采用了基于统计性能的评估方法，得到的结果更为全面、准确。评估结果表明：①通道群时延波动对阵列抗干扰性能影响较小，幅度失配和群时延偏差是导致阵列抗干扰性能下降的主要因素；②群时延偏差的影响基本可以通过增加空时滤波器阶数予以消除，但幅度失配对空时滤波器阶数不敏感；③为减小通道失配对阵列抗干扰性能的影响，建议通过通道校正将幅度波动减小到0.15以内，同时采用9阶空时滤波处理消除群时延偏差的影响。