求解不确定型车辆路径问题的弱鲁棒优化方法
2020-07-13孙亮,王冰,郭栋,徐艺
孙 亮,王 冰,郭 栋,徐 艺
(1. 山东理工大学 交通与车辆工程学院, 山东 淄博 255049;2. 上海大学 机电工程与自动化学院, 上海 200072)
开放式车辆路径问题(Open Vehicle Routing Problem,OVRP)指企业租用车辆来完成针对客户的配送任务,在满足一定约束条件下确定相应的车辆行驶路线以有序服务客户,实现决策目标最优化。企业所租用车辆从企业出发,完成配送任务后,不必返回企业。
从物流配送的实际营运过程看,影响第三方物流模式营运效果的因素主要有两个:①旅行时间的不确定性;②客户期望的服务时间段。因此,针对不确定型OVRP优化方法的研究,对于提升不确定环境下第三方物流模式营运效果具有重要的理论和现实意义。
鲁棒优化方法[1]采用不确定数据的边界特性描述模型参数的不确定性,有效避免了随机优化方法在阐述参数不确定性上过度依赖先验知识及服从概率分布假定的弊端。
目前,求解不确定型车辆路径问题(Vehicle Routing Problem, VRP)的鲁棒优化方法主要包含两类:
1)最坏场景鲁棒优化方法:该方法利用不确定集的边界值,将不确定的优化模型转化为确定的线性规划模型,发现一个对所有观测值可行的最优解,并确保最坏实现下的最优目标函数值达到最优。Sungur等提出了需求不确定的VRP的最坏场景鲁棒优化模型,给出了三种需求限制约束的鲁棒对应式[2]。Hu等提出了描述需求和旅行时间不确定VRP特征的鲁棒优化模型,并分别使用变邻域搜索方法和分支定界法对各自提出的模型进行求解[3]。Agra等针对旅行时间不确定的VRP,提出此类问题的鲁棒优化模型[4]。刘洋等以总服务成本最小化为优化目标,建立了路径规划问题的鲁棒优化模型[5]。Cao等提出针对需求不确定的OVRP的鲁棒优化模型,使用禁忌算法对该模型进行求解[6]。
2) 弱鲁棒优化方法:该方法是以最小的约束违背来保证目标函数值始终不超过合理范围,从而改善最坏值与预期值之间的偏差[7]。Han等提出了基于情景描述旅行时间不确定性的VRP的弱鲁棒优化模型[8-9]。Wu等针对旅行时间不确定的VRP, 提出了一个抑制目标函数恶化程度的弱鲁棒优化模型[10]。
本文以旅行时间不确定的开放式车辆路径问题(Open Vehicle Routing Problems with Uncertain Travel time,OVRP-UT)为研究对象,提出一个描述该问题特征的弱鲁棒优化模型。为了进一步提高启发式算法获取最优解的概率,在超启发式算法的框架下,通过引入预测适应度函数,提出一种自设计遗传算法对弱鲁棒优化模型进行求解。
1 OVRP-UT的弱鲁棒优化模型
1.1 基本定义
定义1惩罚成本:如果配送车辆完成时间超过客户允许的最晚完成时间,根据合同向客户支付的罚金称为惩罚成本。
定义2违约车辆:产生惩罚成本的车辆称为违约车辆。
定义3关于旅行时间的不确定集
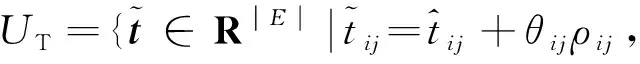
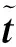
定义4极点:∃x∈UT,对于∀δ>0,x+δ∉UT,则称x是UT的极点。
定义5极点集:UT中由极点构成的子集,用ext(UT)表示。
定义6最坏实现:ext(UT)中极点对应的模型参数的观测值称为最坏实现。
1.2 问题描述
一个完全的赋权图G=(V,E),这里V={0,1,2,…,n}为点集,0表示车场,C={1,2,…,n}表示客户集,客户的数量为n;E={(i,j)|i,j∈V,i≠j}为边集。每一条边赋有一个旅行时间,旅行时间在UT内任意取值。所有车辆具有相同的最大负载Q。每一个客户i赋有一个需求di,di≤Q。企业共租用m辆车来完成配送任务,令M={1,…,m}。Bf是配送任务最晚完成时间,如果配送任务完成时间超过Bf,则会产生惩罚成本。ω1表示单位惩罚成本。
对于UT内的任意实现,该问题的优化目标是为每辆车确定合理的运输路线,使违约车辆数和总惩罚成本的加权和达到最小。调度方案必须满足以下约束条件:
1)调度方案对UT内的任意实现均保持可行;
2)车辆路线始于企业,终止于某个客户,服务完成后,车辆不再返回企业;
3)客户点需求必须且只能由一辆车来服务完成;
4)每一条车辆路线上客户点的需求量之和不超过Q。
1.3 问题建模
1.3.1 决策变量
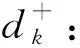
sik:第k辆车到达客户i的时刻。
1.3.2 弱鲁棒优化模型
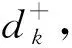
(1)
s.t.
(2)
(3)
(4)
(5)
(6)
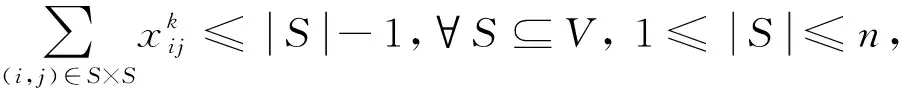
(7)
(8)
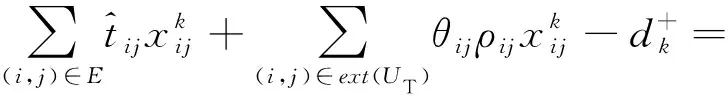
(9)
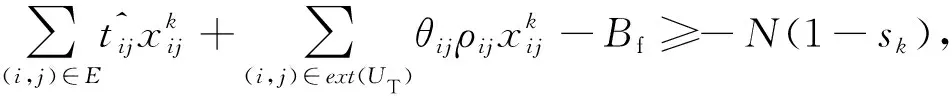
(10)
(11)
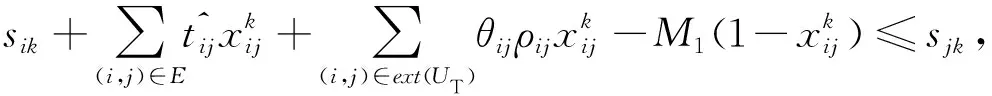
(12)
sik≥0,∀i∈N,∀k∈M
(13)
(14)
(15)
sk∈{0,1},∀k∈M
(16)
根据文献[8]的定义给出另一类弱鲁棒优化模型LRO1如下:
约束条件与NLRO相同。
LRO1的特点在于通过控制违约车辆数,间接实现对总惩罚成本的控制。 不难看出,LRO1是NLRO在ε=0时的特殊情形。
1.4 NLRO的性质分析
性质1ZNLRO表示NLRO的最优解对应的总惩罚成本,ZLRO1表示LRO1的最优解对应的总惩罚成本,ZNLRO≤ZLRO1。
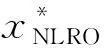
由于
所以
则ZNLRO≤ZLRO1。
□
2 求解方法
自设计遗传算法(Automatic design of Genetic Algorithms, AGA)分为两部分:①根据预期适应度函数值最小的原则,筛选出有利于问题求解的遗传算法的要素;根据适应度函数值最小的原则,筛选出包含当前算法优化解的种群。②将两者组合为一个新的遗传算法,继续对问题进行求解,输出最终算法优化解。
AGA的算法流程如图1所示。
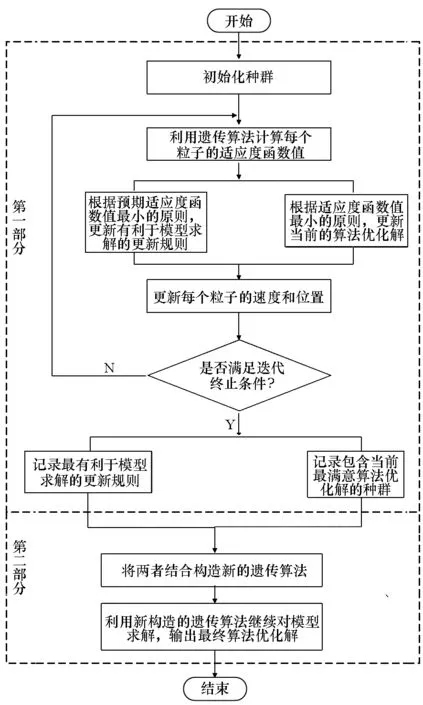
图1 AGA流程图Fig.1 Flow chart of AGA
2.1 遗传算法的关键要素
1)染色体编码方式:染色体共由两部分组成,第一部分采用基于客户的编码方式表示具体的调度方案,第二部分记录该调度方案的适应度函数值。染色体编码结构如图2所示。
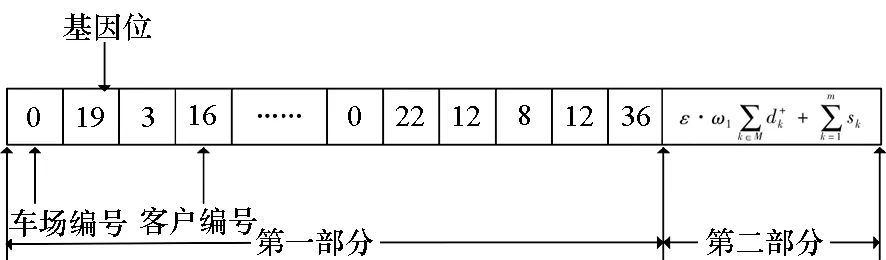
图2 遗传算法染色体编码结构示意Fig.2 Chromosome representation of genetic algorithm
2)染色体解码的具体过程如下:随机生成新序列{i1,…,in},依次将该序列中的客户分配给第1辆车,直到第1辆车的剩余负载无法再为其他客户服务。重复上述过程,直到所有客户都能够被车辆服务。
3)适应度函数的选取:目标函数(1)作为染色体的适应度函数。
2.2 粒子群算法的关键要素
2.2.1 粒子的编码与解码方法
粒子向量由位置向量、速度向量、适应度函数值三部分组成。
1)位置向量:构造1×8维向量X,第1维表示选择因子集合S中的操作类型,第2维表示交叉因子集合Cr中的操作类型,第3维表示变异因子集合Mu中的操作类型,第4维表示遗传算法的种群规模Mga,第5维表示遗传算法的迭代次数Tga,第6维表示选择操作选中的个体数ik,第7维表示交叉概率pc,第8维表示变异概率pm。遗传算子集合及其构成详见表1。
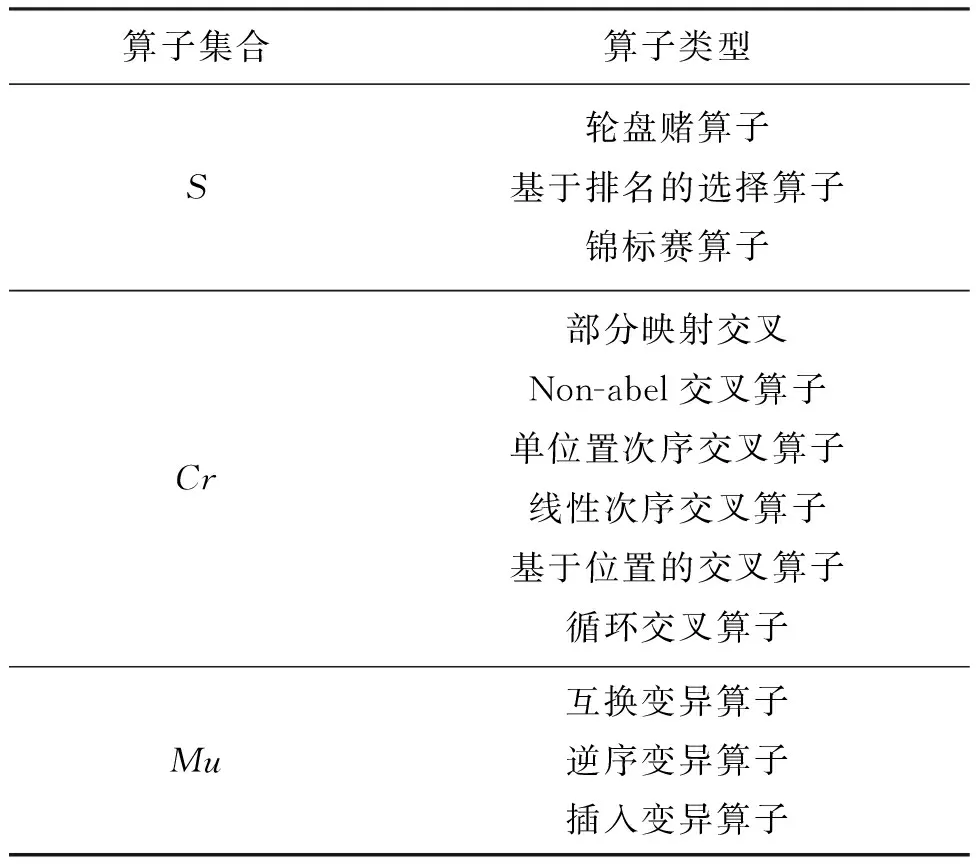
表1 遗传算子集合及其构成
注:不同算子的操作步骤,详见文献[12]。
2)速度向量:速度向量也是一个1×8维向量,用V表示,微粒的运行速度限定在[Vmin,Vmax]。
令
(17)
式中,x0(i)表示该粒子构造的遗传算法的第i次迭代得到的最优适应度函数值。 令x0={x0(1),…,x0(q)},对其做一次累加生成运算,即
令
Y=(x0(2)x0(3) …x0(q))T
则a,b可采用下式计算:
(18)
粒子的编码结构如图3所示。
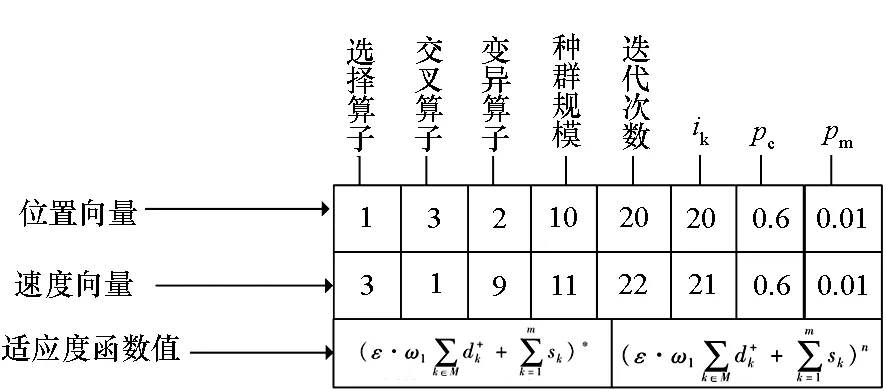
图3 粒子编码结构示意Fig.3 Particle representation
2.2.2 更新规则
速度和位置更新公式为:
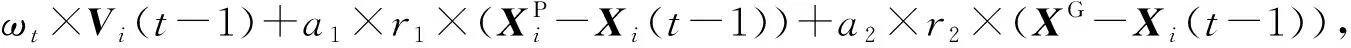
i=1,2,3,4,5,6,7,8
(19)
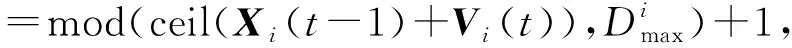
i=1,2,3
(20)
Xi(t)=ceil(Xi(t-1)+Vi(t)),i=4,5,6
(21)
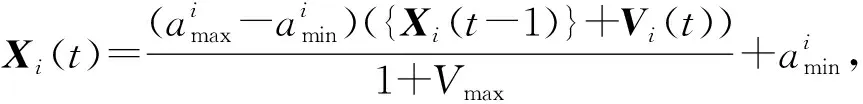
(22)
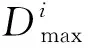
(23)
其中,ω0为惯性因子的初始值,ωe为惯性因子的最终值,T表示粒子群算法迭代的最大次数;r1和r2为(0,1)之间的随机数;a1和a2表示加速因子。
2.3 AGA的算法步骤
AGA的伪代码如算法1所示。

算法1 AGA的伪代码
注:①以粒子的位置向量表示的遗传算法参数作为输入,采用标准遗传算法[12]作为该粒子的解码算法。
2.4 AGA的性质分析
性质2令P(Am)表示第m个粒子所构造的遗传算法能够在有限时间内发现模型最优解的概率,P(Anew)表示新生成遗传算法在有限时间内能够发现模型最优解的概率,
表示AGA发现最优解的概率事件,则AGA发现NLRO的最优解的概率满足如下性质:
P(B)>max{A1,…,AM·T,Anew}
证明:粒子群算法的搜索过程具有隐含并行性,不同粒子的解码过程彼此之间不互相影响,因此,Am和Aj是相互独立的。令P(Ai)=ri,i=1,…,M·T+1,AGA发现最优解的概率为:
又
ri=1-(1-ri)
显然
所以
从而,命题成立。
□
性质3AGA最坏情况下的时间复杂度与遗传算法的时间复杂度相同。
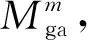
□
性质4AGA最坏情况下的空间复杂度为O(18M+L)。
证明:就空间复杂度而言,每个粒子需要18个变量空间进行存储,另计算适应度函数值需要L个辅助变量空间,从算法1看,AGA存储粒子和生成适应度函数值是重复利用的,因此AGA的空间复杂度为O(18M+L)。
□
3 仿真分析
3.1 仿真环境与参数设置
3.1.1 算例选取与基本参数设置
在对NLRO和LRO1的优化解进行分析时,通常可以借助文献[13]的标准测试数据(C1~C14,O1~O8,vrpnc1~vrpnc14,F11,F12)。此外,还可利用文献[14]的标准测试数据 (A-n34-k5,B-n34-k5)分析不确定参数对NLRO最优解的影响。NLRO和LRO1中确定型参数的取值与标准测试数据中的对应取值相同。令ω1=1,ε=1,θij=3,ρij=1,Λ=225,算法参数信息详见表2。

表2 算法参数设置
遗传算法初始种群的生成方式:首先,随机生成一组满足约束(2)~(8)的调度方案,并记录该组可行解的每一辆车对应的最大配送完成时间Maxroutetimek。其中,Bf采用如下方式生成:
(24)
然后,根据Bf的值,随机生成满足约束(2)~(16)的调度方案,并作为遗传算法的初始种群。
3.1.2 测试环境
用MATLAB R2016a 64位实现了求解NLRO和LRO1的AGA,在 Intel(R) Core(TM) i5-6200U CPU @ 2.3 GHz,8 GB内存的计算机上进行了仿真实验。
3.2 算法优化解的性能分析
针对表2中的模型与算法参数信息,根据表3和表4中的Bf,使用AGA对模型NLRO和LRO1分别独立求解30次,分别取其中的最好解作为各自的算法优化解,该解对应的违约车辆数记录在表3和表4中的veh_n和veh_nl,总惩罚成本分别记录在fc_n和fc_nl这两列中。每一次的运算时间上限设定为3600 s。表3和表4中,cum列表示测试数据的客户数,problem列表示测试数据的名称。
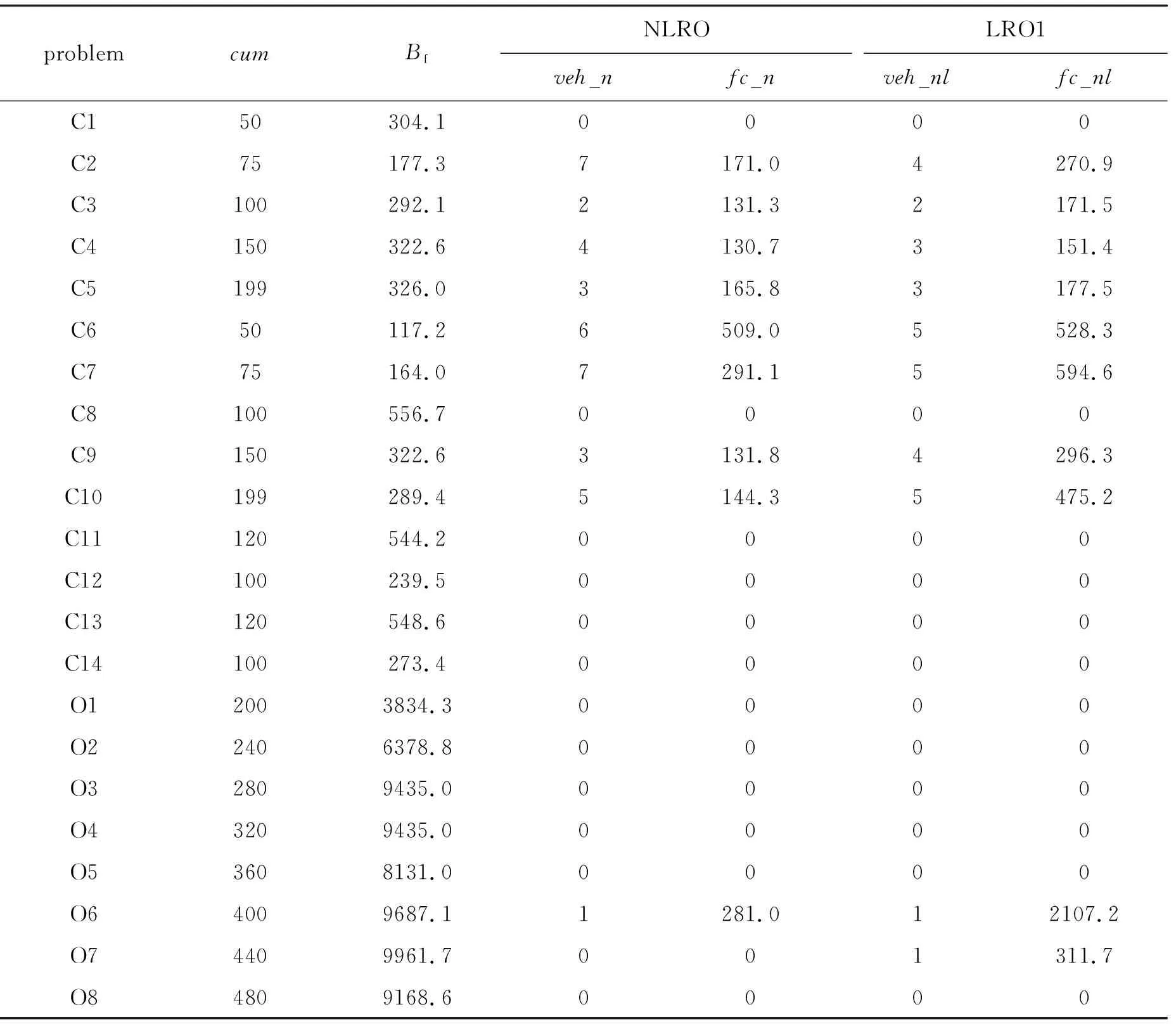
表3 C类和O类问题优化性能分析
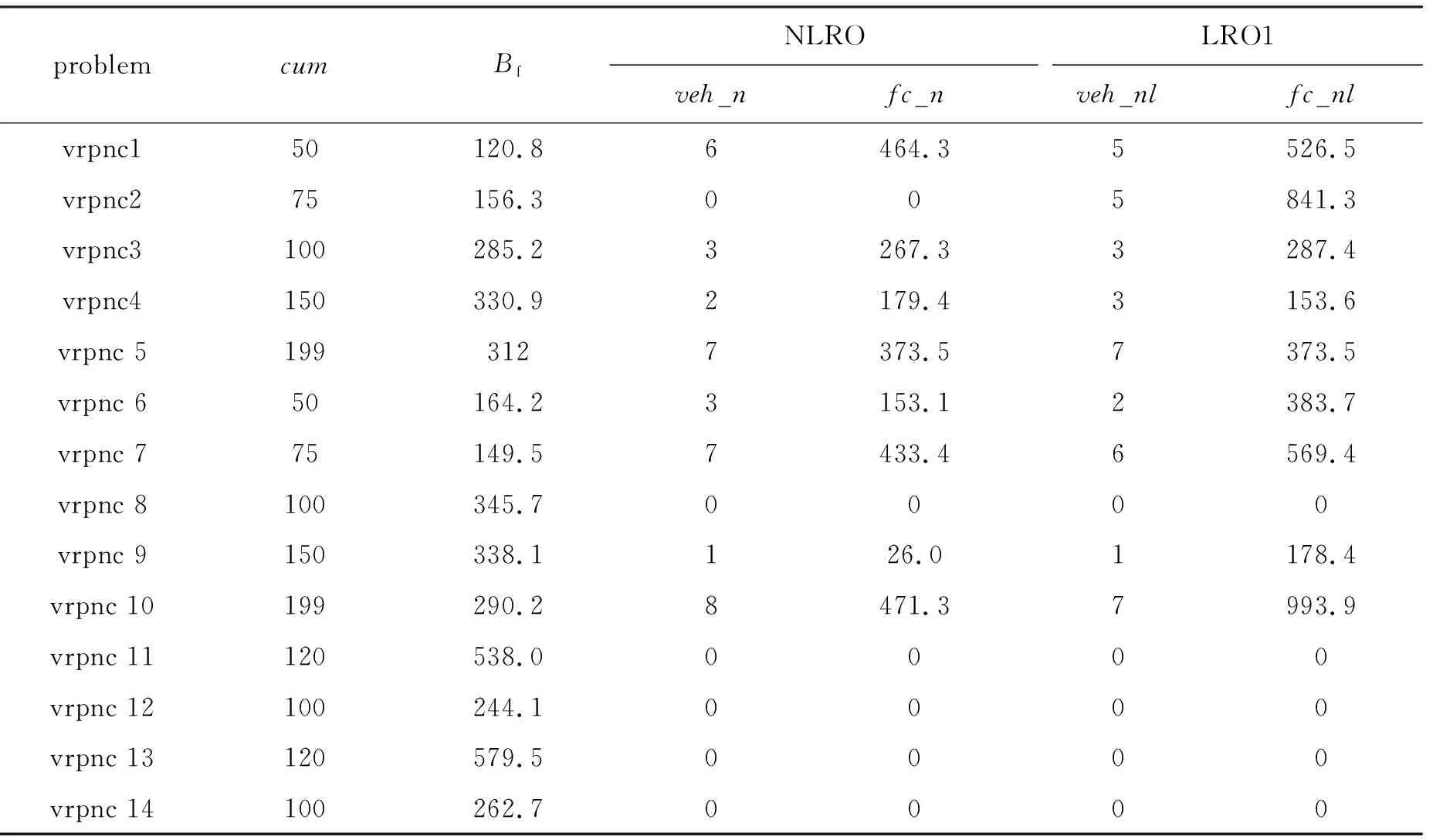
表4 vrpnc问题的优化性能分析
针对表3和表4中veh_n和veh_nl两列数据,利用Wilcoxon秩和检验进行分析,在违约车辆数的优化能力方面,两者无显著差异(p>0.05)。对于表3和表4中fc_n和fc_nl这两列数据,利用Wilcoxon秩和检验进行分析,分析结果表明,NLRO产生的惩罚成本显著小于LRO1(p<0.05)。LRO1单纯以违约车辆数最小为优化目标,可能存在多个违约车辆数相同的算法优化解,当迭代条件终止时,输出的不一定是总惩罚成本最小的算法优化解。与LRO1不同,NLRO兼顾违约车辆数和总惩罚成本两个因素。因此,NLRO算法优化解对应的总惩罚成本低于LRO1。
表3和表4数据表明:对中小规模和大规模测试数据而言,AGA均具有在有限时间内发现最优解的能力。根据性质2,使用AGA求解表2和表3中的算例对应的未发现最优解的概率的范围在[0.000 1,0.000 7]之间,因此,此时的算法优化解表现出了性质1所描述的最优解相类似的性质。
3.3 AGA的求解性能分析
以文献[15]提到的超启发式遗传算法作为AGA的对比算法,记为S-HPSO。使用两种算法对NLRO独立求解30次。S-HPSO与AGA采用相同的初始染色体种群。S-HPSO的相关参数设置详见文献[15]。S-HPSO与AGA遍历的可行解总数相同。其他参数设置详见第3.1小节。分别将两种算法对应的30次运算结果的平均值、标准差、最差适应度函数值、最好适应度函数值、运算时间的均值记录于表5中。表5中标有“*”的测试数据表示算法搜索到最优目标函数值为0的最优解。
在表5中,Avg_a和Avg_s分别表示两种算法在30次运算结果中所有最优适应度函数值的平均值,这两列中的括号内数字表示该测试数据搜索到模型最优解的次数。Std_a和Std_s分别表示两种算法在30次运算结果当中所有最优适应度函数值的标准差。Tavg_a和Tavg_s分别表示两种算法对应的平均运行时间。
对表5中Avg_a和Avg_s这两列数据进行Wilcoxon秩和检验, 结果表明AGA的平均求解性能显著优于S-HPSO的假设成立(p<0.05)。对表5中Tavg_a和Tavg_s这两列数据进行Wilcoxon秩和检验,结果表明两种算法的平均运行时间不存在统计学差异(p>0.05)。虽然AGA增加了利用预期适应度函数筛选更新规则环节,但这部分运算时间的增加不足以引起统计量秩次的变化,因此,两者在平均运算时间上不存在统计学差异。
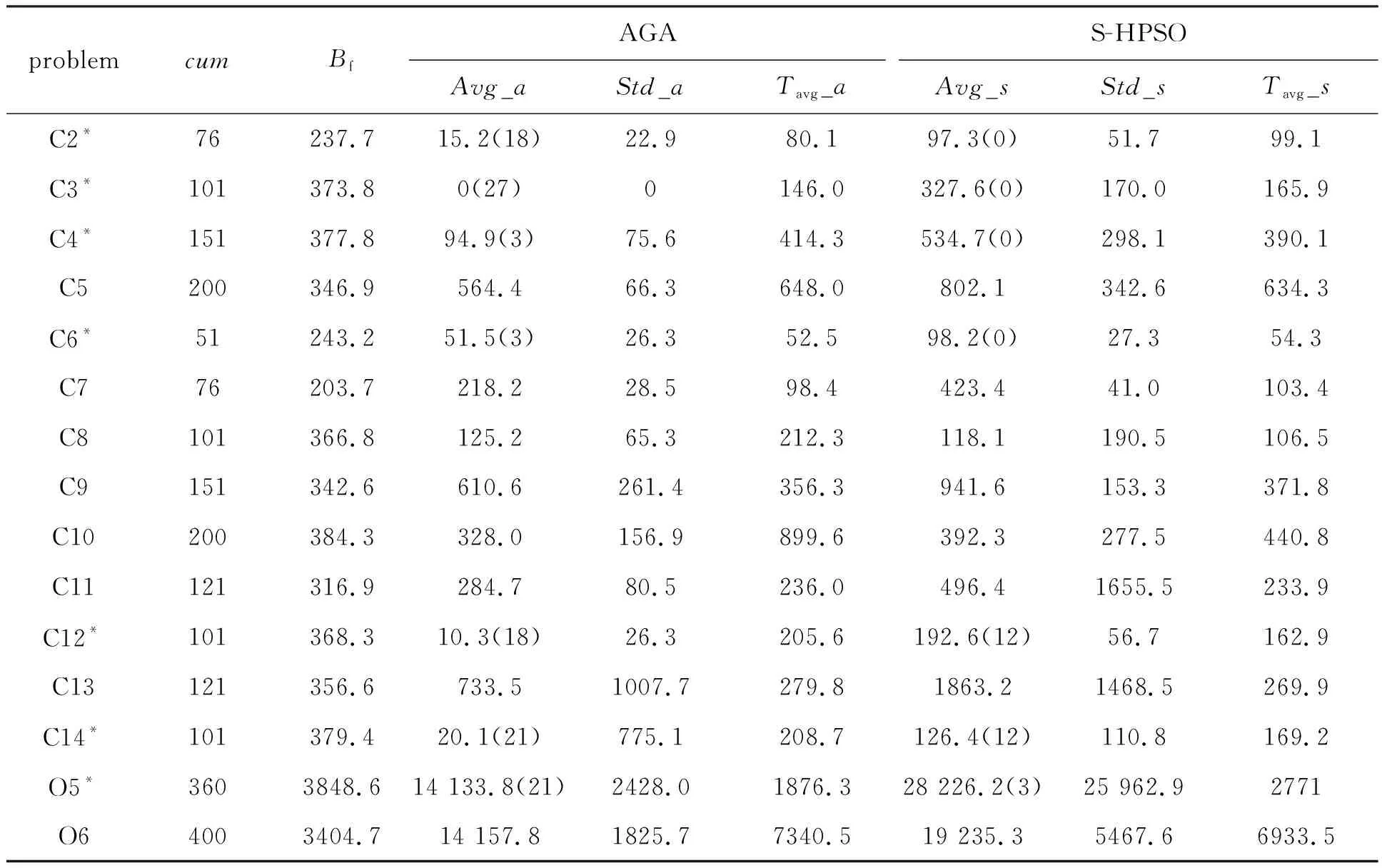
表5 算法统计特性的比较与分析
4 结论
对OVRP-UT建立弱鲁棒优化模型并求解,核心内容如下: ①模型方面,基于现有的弱鲁棒优化的框架构建了针对OVRP-UT的弱鲁棒优化模型;②算法方面,设计AGA求解NLRO,提高了启发式算法发现最优解的概率,且所得算法优化解更接近于最优解。
目前求解不确定型车辆路径问题的鲁棒优化模型的启发式算法主要是元启发式算法,下一步研究应关注如何使用超启发式算法求解不确定型车辆路径问题的鲁棒优化模型。
