初始粗糙面对切向微动行为影响数值研究
2020-07-13黄帅宗沈火明
黄帅宗,刘 娟,沈火明
(西南交通大学力学与工程学院,成都 610031)
微动((Fretting)是指机械振动、疲劳载荷、电磁振动或热循环等交变载荷作用下,接触界面间发生的振幅极小(一般位移幅值为微米量级)的相对运动[1]。切向微动大量存在于实际工程中,其运动幅值微小,且产生的影响不易观察,但其引起的磨损和疲劳损伤所造成的零部件磨损失效不可忽视。
在机械工程中,表面轮廓形貌在微动磨损机理研究中扮演着非常重要的角色,通过对接触体表面轮廓形貌分析,可以确定材料的磨损状态,并能从磨损表面形貌信息中推测出材料损伤失效形式[2]。近年来,一些研究学者发现表面形貌在金属微动磨损机理研究中有着重要的作用[3-5]。
Kubiak K J[6](2010)等人利用通过铣削和光滑磨料抛光过程所形成的表面,在切向微动中研究了全滑移和部分滑移条件下初始表面粗糙度与加工过程对微动的影响。随后,Kubiak K J[7](2011)等人引入磨损活化能的概念,通过试验研究了初始表面粗糙度对摩擦和磨损过程的影响。观察到较高的表面初始粗糙度会使得摩擦系数降低并提高表面材料磨损率。对于越光滑的表面,磨损激活能量越大。在全滑移过程中,较低的表面初始粗糙度可以延缓磨损过程的激活并降低磨损率,但是也会增大摩擦系数。
由于试验研究很难发现微动磨损过程中接触表面的演变规律,因此可以使用有限元方法进行预测。Yue Tongyan[8]等人(2014)对微动磨损中部分滑移和全滑移状态下应力奇异性进行有限元分析。发现应力奇异性与微动机制密切相关,当接触状态处于部分滑移时,应更加注意调整接触界面的网格尺寸来减少应力奇异性的产生;Pereira K[9](2017)等人使用多尺度分析的方法,基于有限元模型研究了粗糙度对微动磨损的影响。结果表明,随着粗糙度的增加,有效接触压力峰值减小而表观接触宽度增加,对于较高的法向载荷条件下,有效接触压力峰值更接近赫兹解析值;Qin W[10](2018)等人通过W-M函数构建分形粗糙表面,研究在钢-钢微动接触中表面粗糙度对局部摩擦和温度分布的影响。研究发现接触表面温升幅值随着粗糙度的增大而增大,材料导热性能越好,接触表面温升幅值越小。
考虑到表面形貌对切向微动磨损有重要的影响,但是以上有限元分析都没有综合考虑表面初始粗糙度和磨损对切向微动的影响。因此本研究可以为研究工程机械中的微动磨损基础力学特性和磨损行为提供参考价值。
本文考虑表面初始粗糙度对切向微动的影响,利用二维Weierstrass-Mandelbrot函数(简称W-M分形函数)建立分形粗糙表面,由UMESHMOTIOM用户子程序引入Archard磨损法则建立二维切向微动数值模型,对微动磨损中的磨损程度进行分析研究。
1 粗糙表面生成
1983年Mandekbrot B提出分形理论[11]。经实验表明,分形理论可以表征许多零件粗糙表面微凸体的形状与分布,并具有连续性、不可微性、尺度不变性和自相关性特征。二维表面轮廓由W-M函数给出[12]。
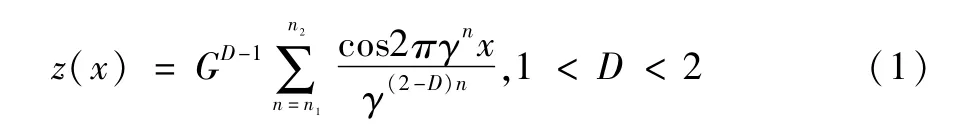
式(1)中,z(x)为随机表面轮廓高度;x表示轮廓的位置坐标;G是反映表面轮廓振幅的分形尺度系数;D是决定高频和低频分量在表面轮廓中的相对比重的分形维数(1<D<2);γ控制表面轮廓中频率的密度,对于大多数表面轮廓,γ取1.5较为合适[12];n是分形尺度指数 ,n1和n2代表最低和最高截止频率指数。令ω为轮廓空间频率且ω=γn,那么ωL为起始频率,由样本长度L确定且ωL=1/L,ωU是频率上限,由轮廓分辨率δ确定且ωU=δ/2。若一条被模拟的粗糙轮廓曲线的均方根为Rq,则特征尺度系数G可由方程(2)[2]确定,故可以根据D和G求出粗糙面的轮廓均方根Rq。
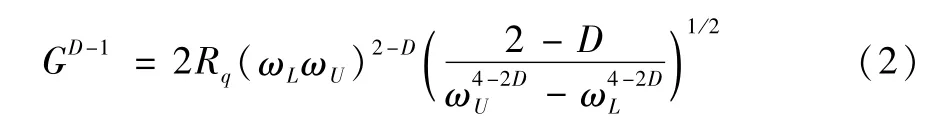
本文中,取G=2.85E-4μm,D=1.5,δ=0.5μm,L=[50,170](μm),则n=[-11,0],生成的粗糙表面轮廓曲线如图1所示,轮廓均方根Rq为0.1302μm。
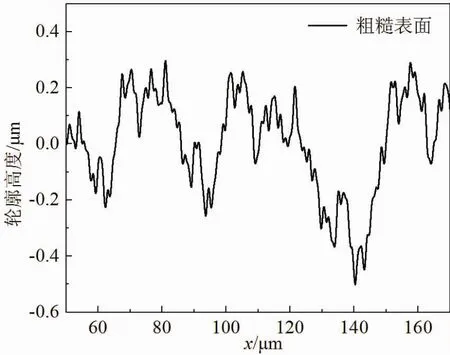
图1 粗糙表面轮廓曲线
2 有限元模型
2.1 有限元模型建立
二维柱-平面切向微动有限元模型如图2所示。考虑到分形函数生成的粗糙表面有很多微凸体,施加载荷后,可能会造成接触失败与网格严重畸变,故利用python中的scipy模块对轮廓曲线进行插值优化。为了保证计算精度,对接触区网格进行细分,细分后的网格尺寸为0.25μm,单元类型选择CPE4。半圆柱半径为1200μm,平板尺寸为2400μm×1200μm。为了减少计算量,降低磨损计算时间,仅在平板接触表面中心区域(长120μm)生成粗糙面。平板和半圆柱材料分别是AISI1034和AISI52100,材料参数如表1所示,其中硬度(H)为屈服强度的2.8倍[13]。
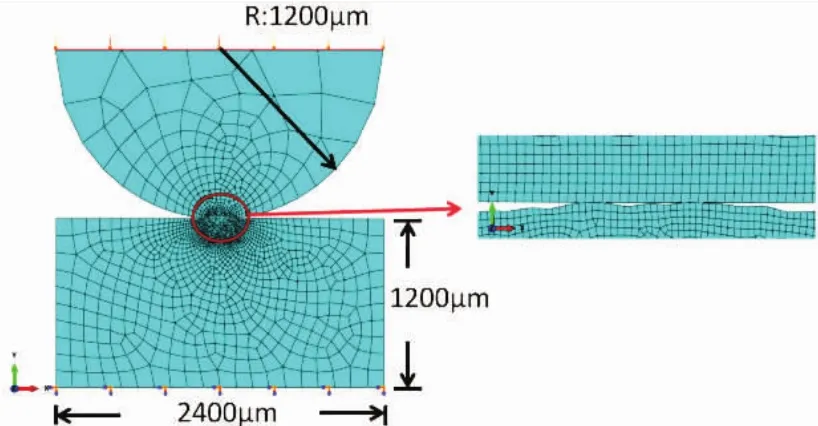
图2 有限元模型
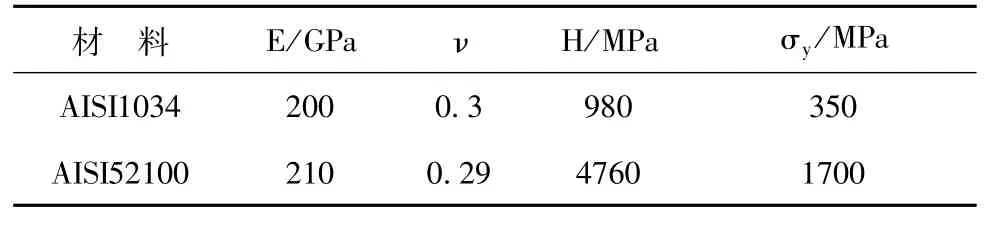
表1 材料参数
为使半圆柱体均匀下压,故将半圆柱上表面与参考点建立刚体绑定约束,对参考点施加法向载荷F和切向周期位移载荷u。加载过程如图3所示。其中0-1表示压紧阶段,在参考点上施加Y轴负向法向载荷F;1-2表示切向微动阶段,参考点上施加法向载荷F和X方向周期性位移载荷u;2-3表示卸载阶段。
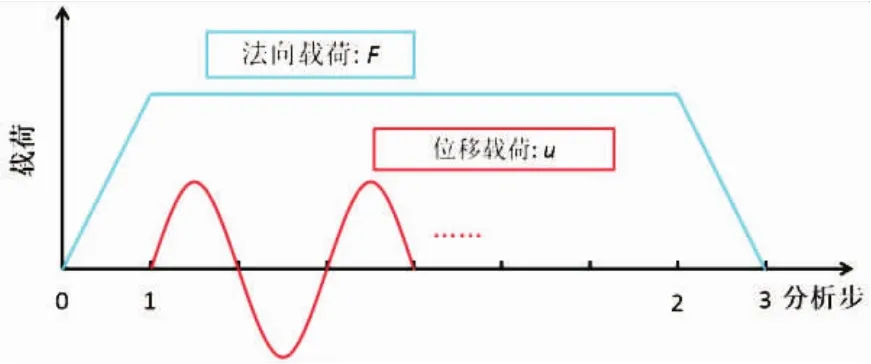
图3 加载曲线
为了接触过程中同时考虑主面和从面的形状变化,不会因为过度渗透而导致结果不准确,故半圆柱和平板接触部分设置为主面-从面接触,其中粗糙平板为从面,半圆柱光滑面为主面。离散方法采用面对面离散。法向接触使用硬接触,约束方法使用增广Lagrange法,并允许接触后可以分离;切向接触使用各项同性的库伦摩擦公式,摩擦系数为0.5。
本文磨损模型如式(3)[14]所示:
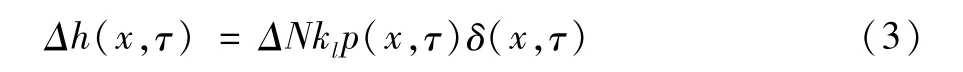
其中 τ为时间,Δh(x,τ)为磨损深度增量,p(x,τ)为接触应力,δ(x,τ)为相对滑动,ki为磨损系数,ΔN为循环跳跃系数。本文中为不类似的两个金属接触,因此磨损系数ki为6.7e-5[15]。UMESHMOTION将式(3)所计算出的节点磨损量作为节点偏移量进行网格调整。通过重复此过程便可实现对磨损程度的有限元预测,具体流程如图4所示。
2.2 有限元模型验证
在Y-K分形粗糙表面接触模型[13]中,存在一个临界接触面积a′c,如式(4)所示:
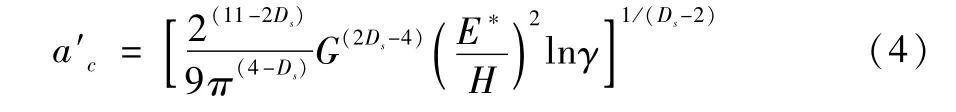
当最大微凸体截断面积a′L大于a′c时:(a)Ds=2.5(D=1.5),弹性部分作用力Fe与塑性部分作用力Fp分别如式(5)与式(7)所示;(b)Ds≠2.5(D≠1.5),弹性部分作用力Fe与塑性部分作用力Fp如式(6)与式(7)所示。当最大微凸体截断面积a′L小于等于a′c时,弹性部分作用力Fe为0,塑性部分作用力Fp如式(7)所示。
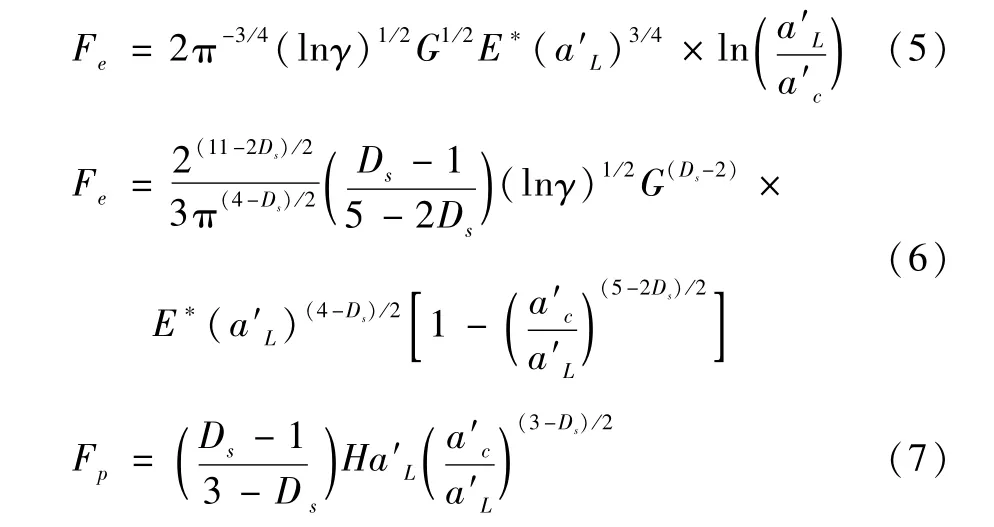
对总作用力F和接触面积A进行无量纲化处理:复合弹性模量E′=E/(1-v2),无量纲接触面积A′=A/A0,无量纲应力P′=F/(A′×E′)。模型验证中,试样长度L=120μm,G=0.12μm,Ds=2.5(D=1.5),γ=1.5,变形体材料参数为E=210 GPa,ν=0.3,H=1834 MPa。
如图5所示,将无量纲化载荷与接触面积有限元结果和解析解对比,两者具有较好一致性,故验证了本模型的合理性。
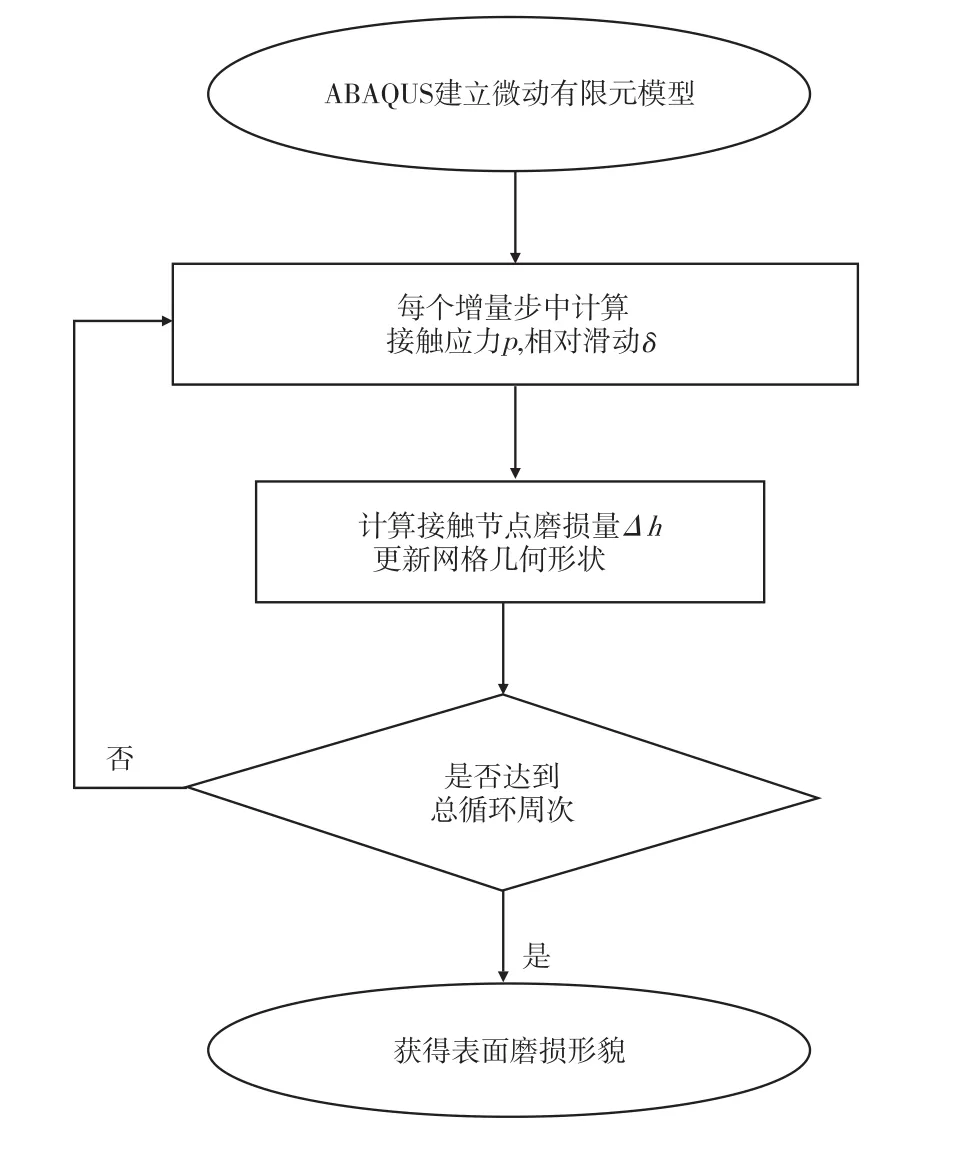
图4 微动磨损有限元分析流程图
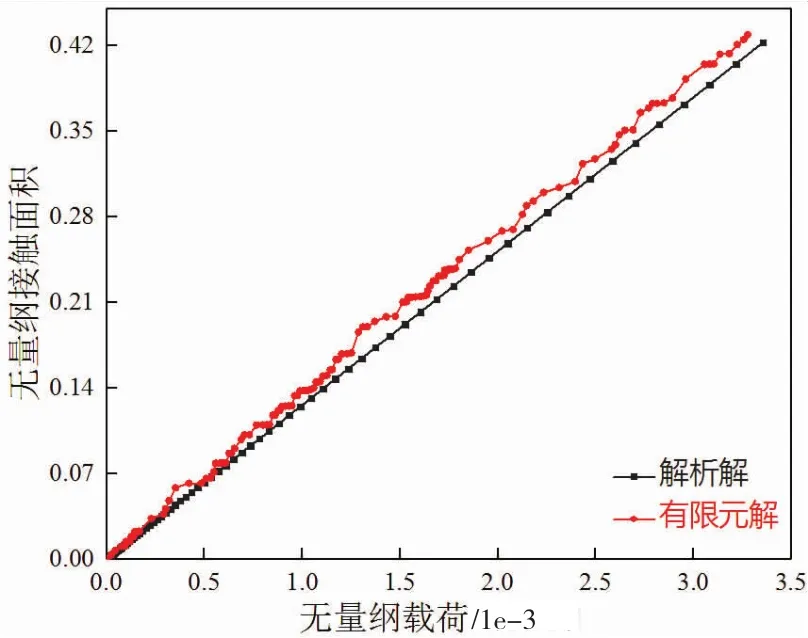
图5 有限元结果与解析解对比
3 结果分析
3.1 粗糙面对磨损的影响
图6可以看出,微动循环后的粗糙表面与光滑表面磨损区域和磨损形貌基本一致。两者磨损区域外的表面由于受到相邻微凸体的挤压均发生塑性变形而突起。
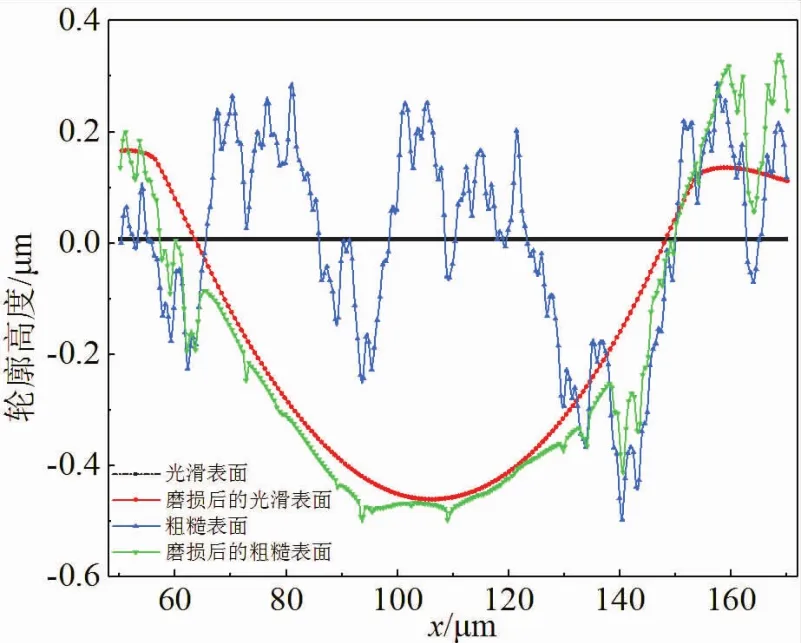
图6 100次循环后光滑表面与粗糙表面磨损形貌对比:F=60 mN,u=4μm,t=3 s
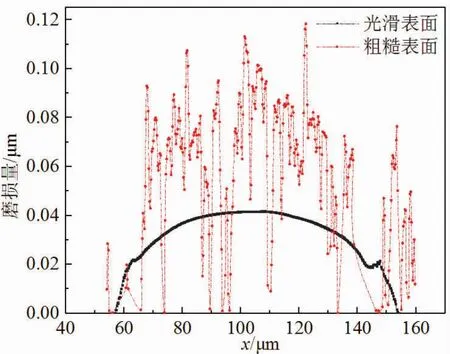
图7 100次循环后光滑表面与粗糙表面磨损量对比:F=60 mN,u=4μm,t=3 s
在图7中,光滑表面磨损量明显比粗糙表面磨损量小,两者均呈现出自中心区域逐渐减小的趋势。初始表面为粗糙面,则粗糙峰会引起接触应力的不均匀分布,并产生强烈的应力集中,导致磨损量的分布具有离散性。初始光滑面与粗糙面下的接触应力分布具体如图8所示。粗糙表面微凸体的分布对磨损区域和磨损形貌也有一定影响。在图6与图7中,x=138μm附近左侧的微凸体明显较高,因此在法向载荷作用下,左侧表面发生磨损,磨损后的表面低于磨损前的表面;右侧表面没有发生磨损,在相邻微凸体的挤压下,微动循环后的表面高于磨损前的表面。
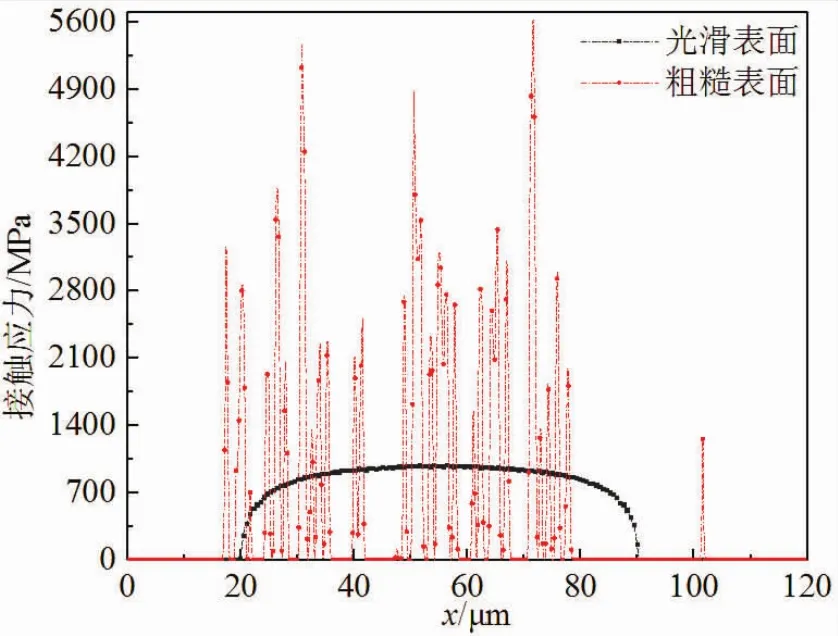
图8 光滑表面与粗糙表面接触应力分布对比:F=60 mN,u=4μm,t=1 s
3.2 微动工况对磨损的影响
图9和图10分别表示不同法向载荷下的磨损量和等效塑性应变对比。结果表明,随着法向载荷的增加,接触中心区域磨损量和等效塑性应变差别较小,接触区域边缘磨损量和等效塑性应变差别较大。这是因为,粗糙峰在微动过程中会产生强烈的应力集中,在一定量的微动循环后,在应力集中明显的接触中心区域,其磨损程度较高,微凸体高度趋于一致,在一定范围内法向载荷的增加对接触中心区域的应力集中影响较小。而接触边缘趋于磨损程度较低,微凸体之间差异较大,在一定范围内法向载荷的增加对接触中心区域的应力集中影响较大。
图11和图12分别表示不同切向位移幅值下的磨损量和等效塑性应变对比。由图可见,位移幅值在一定范围内变化时,等效塑性应变变化不大,而磨损量显著增加。这是因为同一法向载荷下,接触区域的应力水平基本不变,而切向位移幅值的增加导致半圆柱和微凸体相对位移增加,使得磨损量显著增加。
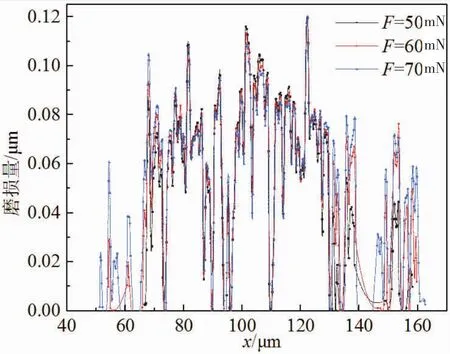
图9 100次循环后不同法向载荷下磨损量对比:u=4μm,t=3 s
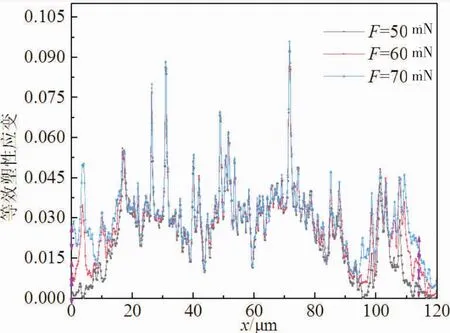
图10 100次循环后不同法向载荷下等效塑性应变对比:u=4μm,t=3 s
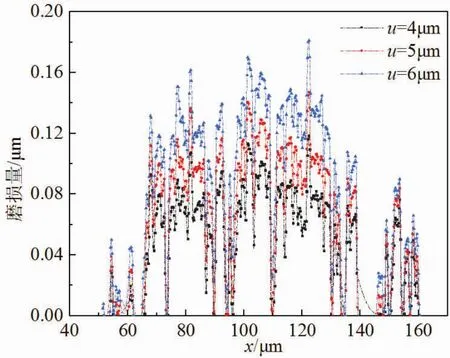
图11 100次循环后不同位移幅值下磨损量对比:F=60 mN,t=3 s
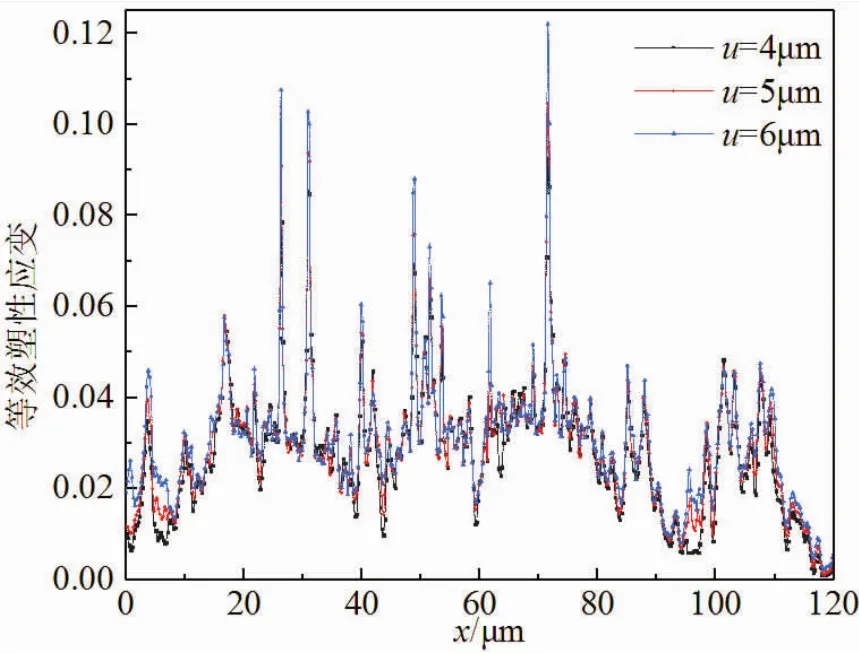
图12 100次循环后不同位移幅值下等效塑性应变对比:F=60 mN,t=3 s
4 结论
建立分形粗糙表面数值模型,对二维切向微动下磨损程度进行分析,主要结论如下:
(1)光滑表面磨损量明显比粗糙表面磨损量小,两者均呈现出自中心区域逐渐减小的趋势,且粗糙表面磨损量分布有很大的的离散性。这是因为,初始表面为粗糙面时,粗糙峰会引起接触应力和摩擦切应力的不均匀分布,并产生强烈的应力集中,导致磨损量显著变大并具有离散性。
(2)初始表面为粗糙面时,由于微凸体的高度与分布具有不均匀性与随机性,接触时产生强烈的应力集中,较大的塑性变形使得粗糙表面和光滑平面磨损形貌差异不大。
(3)在一定载荷范围内,法向载荷的增加对接触中心区域磨损程度影响较小,而对接触边缘区域磨损程度影响较大。这是因为随着微动磨损的进行,磨损严重的接触中心区域微凸体高度趋于一致,一定范围的载荷增加对其应力水平影响较小。
(4)切向位移载荷的增加使得磨损程度明显变大。这是因为切向位移幅值的增加导致半圆柱和粗糙表面微凸体相对滑动变大,导致磨损量增加。
