基于旋转高频注入的IPMSM位置检测改进研究
2020-07-13杜大宝高文根胡明星吴长林
杜大宝,高文根,胡明星,吴长林
(安徽工程大学电气工程学院,安徽 芜湖 241000)
引言
内置式永磁同步电机(Interior Permanent Magnet Synchronous Machines,IPMSM)由于其高转矩密度、快速动态响应和控制简单而在新能源汽车领域具有广阔的应用前景[1-3]。为了实现高性能的IPMSM的矢量控制,必须要获知电机的转子位置和速度,而获知电机的转子位置信息,通常需要通过旋转变压器或编码器等位置传感器来获取。然而,位置传感器的存在也降低了系统的可靠性和抗干扰能力,更有需要维护和成本等问题[4-5]。为了拓宽PMSM的应用范围,关于永磁同步电机无位置传感器控制方案的研究是一个研究的热点和难点。
无位置传感的控制根据电机运行的范围,可分为两种:(1)无信号激励法[6-9],这一类方法利用电机的反电动势直接或间接地估算转子的磁极位置,但反电动势和电机的转速相关,故在零速或低速时有用信号信噪比低,导致估算精度过低而无法获取转子信息,所以该方法只能应用于中高速;(2)高频信号注入法[10-15],该方法根据永磁同步电机的凸极特性,为得到电流响应信号向电枢注入高频激励信号,估算出转子的位置,其中注入的方式可以是旋转电压注入法也可以是脉振高频电压注入法。因其对电机参数需求小、零速和低速控制能力强,成为了低速范围的主要估算转子位磁极位置的方法。目前,国内外众多专家对注入高频激励法进行了研究与改进。文献[11]采取旋转高频信号注入法来对IPMSM进行转子的位置及速度估计,再对负相序相应信号进行提取来实现转子转速信息的估计,通过同步轴系带通滤波器和巴特沃斯滤波器来完成;文献[12]提出了一种改进的位置检测算法,该算法使用延迟信号消除(DSC)方法对高频信号即高频电流信号进行滤波。d轴可以用于解调q轴的电流信号以获得转子位置误差。最后,通过锁相环(PLL)获得转子的当前位置;在文献[15]中,永磁同步电动机(PMSM)在全速范围内的转子位置和速度估算是通过将旋转高频注入方法与滑模观测器相结合来完成的,换向的控制策略被用于复合算法的过渡区域,来准确估计转子的磁极位置信息。
为了简化系统的设计过程,减少多个滤波器的使用,降低系统相位延迟,提高转子磁极位置估计精度,在分析旋转高频信号注入控制算法后,借助IIR数字滤波器取代同步轴系带通滤波器。IIR数字滤波器的设计可以依靠成熟模拟滤波器的设计方案,通过查表模拟滤波器,把模拟滤波器的公式通过脉冲响应不变法和双线性变换法等转换规则,转换成数字滤波器的设计公式,极大地减少了数字滤波器的设计步骤,再补偿IIR的相位延迟。根据实际需求,借助MATLAB中的滤波器设计和分析工具箱设计数字滤波器。最后,把设计的滤波器输入到搭建的IPMSM无位置传感器的MTPA控制的系统仿真中,以验证优化方案的有效性。
1 基本原理
1.1 矢量控制
矢量控制的基本思想是模拟直流双闭环控制原理来控制交流电动机,并采用坐标变换,使复杂的交流电动机的模型变得简单,与直流电动机的转矩控制一样快且准确。矢量控制是将定子电流的矢量解耦为产生磁场的励磁电流分量和产生转矩的转矩电流量,并分别控制两个分量的幅值和相位,从而实现对电机转矩的控制。
PMSM转子的磁场是由磁场和定子电流的两个分量来决定的,永磁体的磁链保持不变,所以对电机转矩的控制可以变为对电流的两个分量的控制,故矢量控制策略可以分为很多种。对于矢量控制算法,本文选用了最大转矩电流比。在控制策略中,通过电流和转矩的公式获得最值,它充分利用了凸极电动机的磁阻转矩,是对凸极电动机中矢量控制的优化,提高逆变器电压的利用率,减少损耗,提高电机的效率。
1.2 旋转高频激励注入
将三相高频旋转电压激励添加到电机的定子绕组中,得到与之相对应的高频响应。基于PMSM电机的凸极效应,不同位置得到的高频电流响应也不相同,且电流响应中含有与转子位置信息有关的有用信息。高频电流响应通过同步轴系高通滤波器(SFF),得到负相序电流响应,再通过外差法获得转子位置角误差响应,最后估计的转子角度信息,利用龙贝格观测器获得。旋转高频电压注入的结构框图如图1所示。
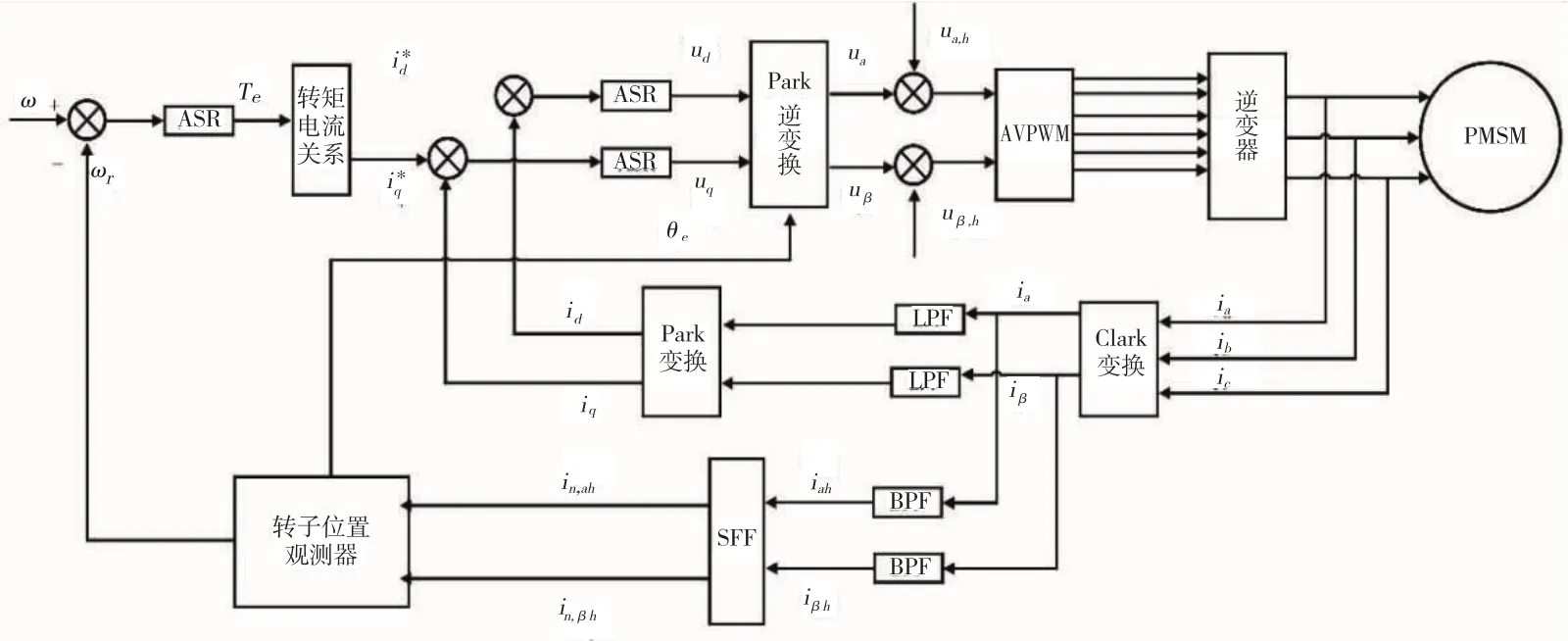
图1 IPMSM无传感器控制系统结构框图
逆变器的开关频率、基波的最大频率以及估测的带 宽,都会影响到注入的高频载波信号的频率的选择。为了避免产生噪声,需要注入信号的最大频率大于逆变器开关频率的一半。为了限制最大载波信号频率,需要增加载波频率和降低信噪比。为了容易分离载波信号与基频信号,注入的载波频率不能太低,故注入的高频信号频率为0.5 kHz~2.0 kHz。高频信号注入过程中,定子电阻可以忽略,在这种情况下,将PMSM高频注入下的电压信号表示为:

假定注入信号的频率为ωh、幅值为vh,那么注入的高频电压信号表达式为:
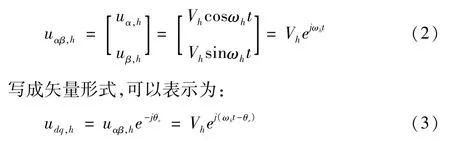
旋转高频电压激励下PMSM的电流响应为:

1.3 观测器的位置估计
向电机注入高频激励,被凸极调制后的高频电流响应包括两种类型的分量:一是没有携带转子信息的正相序的分量,二是有携带转子信息的负相序的分量。正相序分量为ej(ωht-π2),负相序分量为ej(2θe-ωht+π2),电流响应的两个分量旋转的方向相反,但它们都包含ωht,两个分量都属于高频电流。因此,不能使用一般的滤波器将它们分离,可以先使用带通滤波器滤除基波电流和载波频率,利用同步轴系高通滤波器进行滤波处理以检测转子位置。将冗余信号转换到同步旋转的坐标系上,这些信号就会变成直流量,通过高通滤波器滤掉,得到需要的电流信号向量为:
天津滨海新区是国家发展战略的重要一极,是中国的,更是世界的。一个面向世界的国际化城市不能没有自己的城市品牌,特别是在西方发达城市普遍重视建设自己的城市品牌的形式下,天津滨海新区城市品牌的建设显得尤为重要,也尤为迫切。

采用外差法提取转子位置误差信号,利用转子位置观测器进一步滤波和处理后,估计转子的位置误差信号为:


设置跟踪误差信号,当高频载波电流的负相序分量与高频载波电流分开时,通过负相序分量估算转子磁极的位置。为了准确估测转子的位置和速度信息,可利用龙贝格观测器观测转子磁极的位置。为了提高观测器性能,在传统的龙贝格观测器的基础上设计了一种改进的龙贝格观测器,额外的添加一个积分项在位置观测器的控制器中,如图2所示,既可提高系统的动态能力,也可提高龙贝格转子位置观测器的抗干扰性能,PIID控制器的控制器取代了原有的观测器。改进后观测器的传递函数为:

其中:J是转动惯量;是转动惯量估计值;s为复变量;kd是调节器的微分系数;kp是比例放大系数;ki是积分系数;kii是额外的积分系数。
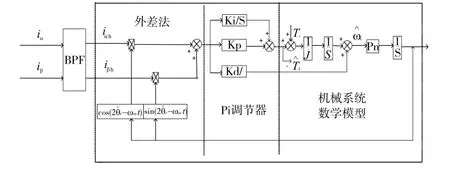
图2 转子位置跟踪观测器的标量形式的实现框图
2 IIR数字滤波器及线性相位补偿
2.1 IIR数字滤波器设计
注入旋转高频电压信号,将转子位置误差信号送入到转子位置观测器中。而准确估计转子的位置信号,需要依赖滤波器对信号的处理能力。为了保证系统复杂程度低和高频响应信号相位滞后小,采用了IIR数字滤波器提取高频响应信号。将IIR数字滤波器引入高频注入中,减小了通带和阻带之间的误差,使得在相同阶次下误差最小,它的线性相位特性和快速响应特性也最大限度地提高了系统的性能。
为了降低系统的相位延迟,在低阶次中有着良好的系统跟随性,设计了一个带通滤波器,以此准确估算转子的位置信息,如图3所示。在实际应用中,IIR数字滤波器可以通过软件程序实现滤波,以减少滤波器的使用。借助模拟滤波器的设计方法设计了IIR数字滤波器,根据已有的计算公式,查询图表给出了设计规则,转变成数字滤波器。设计出符合条件的技术指标设计模拟滤波器H(s),再根据s与z的规则将H(s)转化为H(z),常见的有巴特沃斯型、切比雪夫Ⅰ型、切比雪夫Ⅱ型以及椭圆型等模拟低通滤波器。这些低通滤波器根据规则变换,带阻滤波器、带通滤波器和高通滤波器的转换都是用冲激响应不变法、阶跃响应不变法和双线性变换法,模拟频率的变换将s转化成z,从而完成数字滤波器的设计。

图3 数字滤波器的设计步骤
本文选用巴特沃斯数字滤波器,其低通滤波器函数见表1。以冲激响应不变法将巴特沃斯型低通滤波器转换为IIR数字滤波器,注入的高频激励信号频率为1000 Hz。模拟滤波器的技术指标中:通带频率为 [Ωfc1,Ωfc2]=[950 Hz,1050 Hz],两个角频率分别为 Ωfc1=1900π和Ωfc2=2100π,参 考 频 率 Ωf0=中心频率Ωfr=Ωfc2-Ωfc1,滤波器的阶数N=2。

表1 巴特沃斯型低通滤波器N阶函数
图4为选用巴特沃斯模拟低通滤波器,再用冲激响应不变法得到的IIR数字滤波器的频率响应曲线图。由图4可知,滤波器具有好的线性相位特性和快速响应特性。
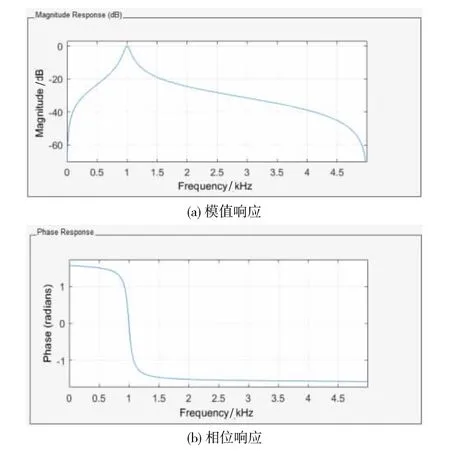
图4 IIR滤波器频率响应曲线
IIR滤波器的冲激响应系数为:
a=(0.028 0.053 0.071 0.053 0.028)
b=(1.000-2.026 2.148-1.159 0.279)
根据表1可得二阶低通滤波器系统函数:
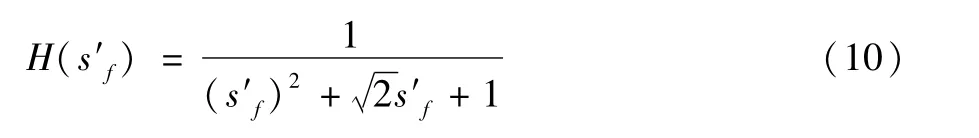
其中:s′f=sf/Ωfc是滤波器的归一化复频率,Ωfc为滤波器的截止频率。模拟低通滤波器通过频率变换关系转换成带通数字滤波器可以得到二阶带通数字滤波器的系统函数:
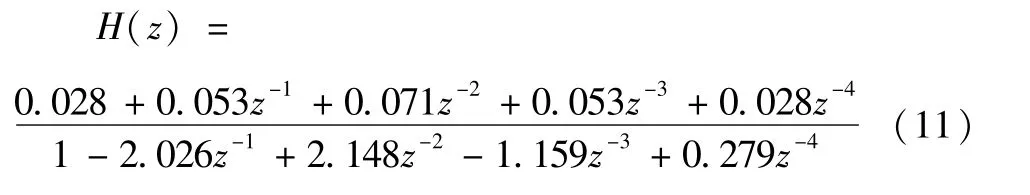
2.2 线性相位补偿
在三相高频旋转激励注入电机基波中的检测准确度容易对电机转子位置的辨识产生影响,如信号解调过程中IIR数字滤波器引起的延时引起转子位置估计值与实际值不符。在IIR数字滤波器的基础上,提出了转子位置误差信号线性相位补偿策略,以便有效地减小延时造成的相位延迟,同时对转子位置估计的误差值进行相位补偿,提高转子位置信息的估计准确度。转子速度和采样时间决定了补偿角度,如:
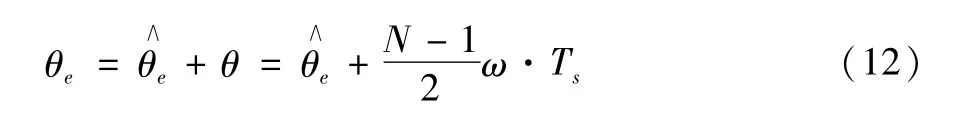
其中:θ·T为系统补偿角度。s
3 系统仿真
转高频电压信号注入的控制模型,分别如图5和图6所示。

表2 电机参数
3.1 仿真模型
系统的仿真模型采用PMSM矢量控制的最大转矩电流比方式,电机参数见表2。
给定注入的高频信号幅值为20 V,高频电压信号频率为1000 Hz,算法采用了ode45。在Simulink中搭建了传统的旋转高频电压信号注入的控制模型与改进的旋
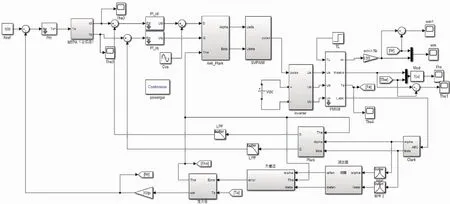
图5 IPMSM无传感器控制系统位置检测研究的仿真模型

图6 IPMSM无传感器控制系统位置检测改进研究的仿真模型
下面在相同的电机参数下,对搭建的旋转高频电压信号注入下无传感器控制仿真模型和基于IIR数字滤波器的位置估计控制仿真模型进行转子位置自检测的波形比较分析。
3.2 仿真波形及分析
给定转速均为100 r/min,仿真时间0.4 s,对 PMSM无传感器的高频激励注入的控制和基于IIR数字滤波器的位置检测改进的控制进行仿真。
3.2.1 转子位置估计波形分析
采用旋转高频注入的IPMSM位置检测的转子位置估计波形如图7所示,基于IIR数字滤波器的位置检测改进控制算法的转子位置估计波形如图8所示。
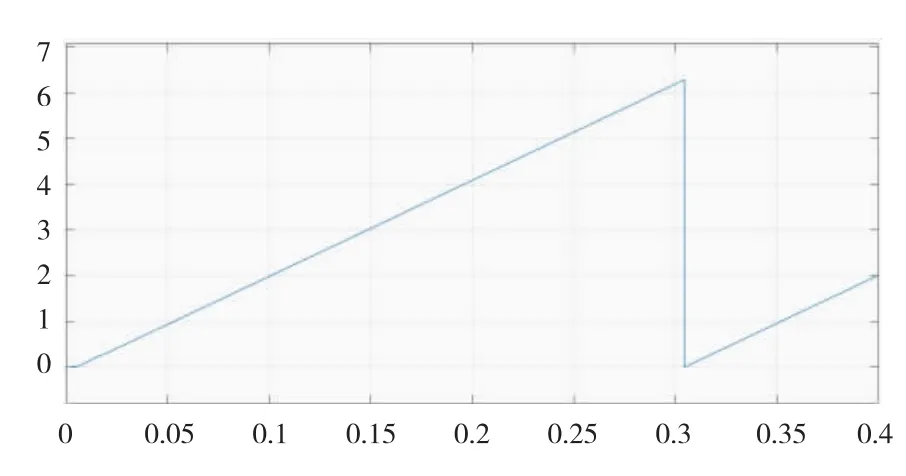
图7 转子位置观测器估计波形
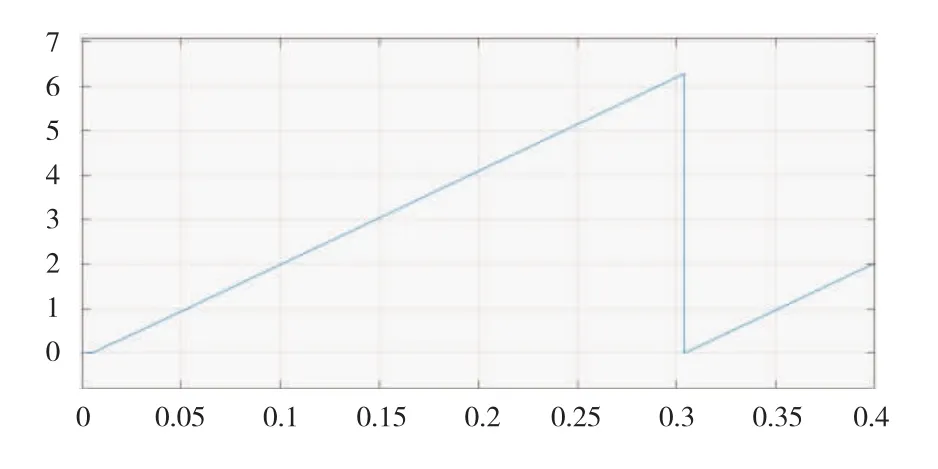
图8 转子位置观测器的改进估计波形
由图7和图8可知,与使用旋转高频信号注入法中同步轴系带通滤波器的位置估计波形相比较,基于IIR数字滤波器的位置改进算法对转子的位置估计波形基本相同,却减少了滤波器的使用,降低系统的复杂性。
3.2.2 转子位置误差波形分析
采用旋转高频注入的IPMSM位置检测的转子位置误差波形如图9所示,基于IIR数字滤波器的位置检测改进控制算法的转子位置误差波形如图10所示。
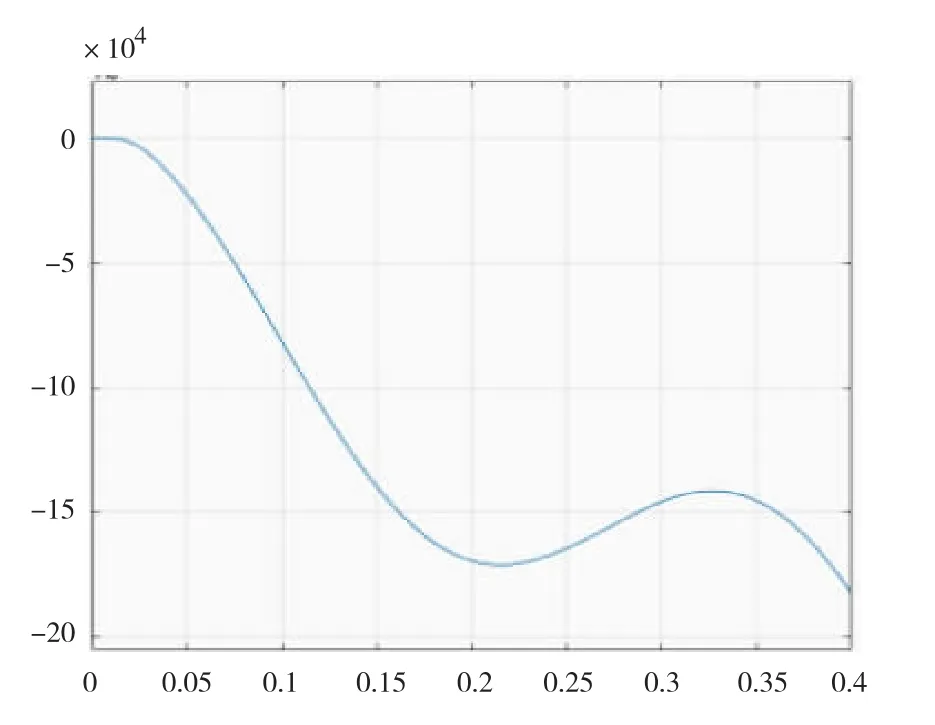
图9 转子位置误差波形
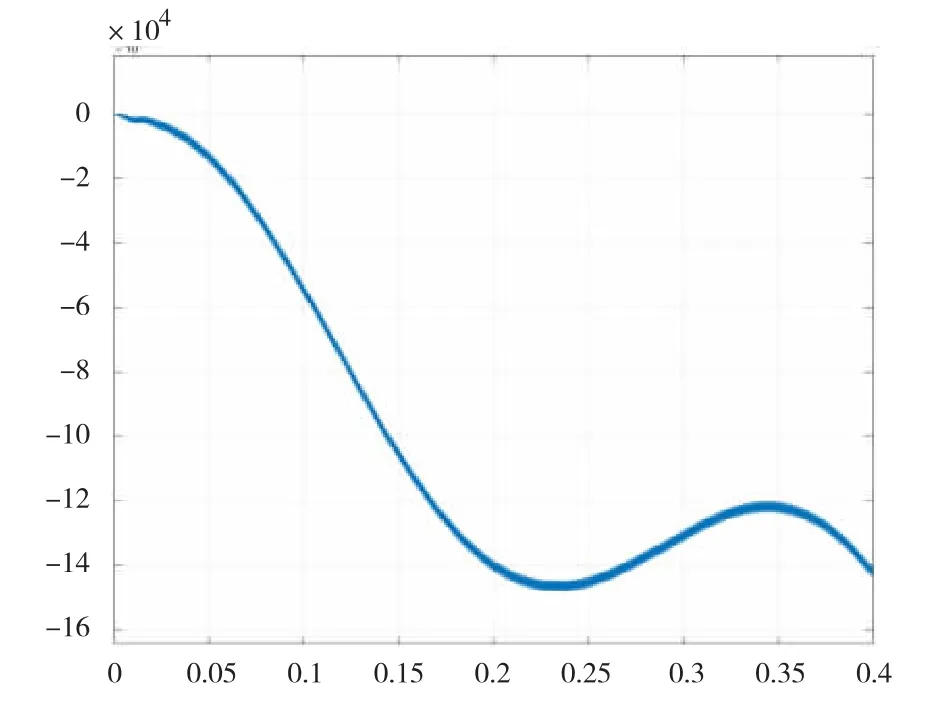
图10 改进的转子位置误差波形
由图9和图10可知,与使用传统旋转高频信号注入法的转子位置估计的位置误差波形相比,改进的转子位置估计的位置误差更小。线性相位补偿策略有效地减小了延时造成的相位延迟,并对转子位置估计的角度进行了相位补偿,使转子位置的估计更准确。
4 结束语
本文提出了基于IIR数字滤波器的改进转子位置自检测来运行无位置传感器永磁同步电机,省去了多个滤波器的使用,并且降低了系统的延时。通过设计IIR数字滤波器来滤出高频电流响应,可以最大程度地提高转子位置估计的准确度。最小转子速度延迟和位置估计是通过线性相位补偿实现的。最后构建了无传感器矢量控制的PMSM的仿真模型,实验结果表明本文所提出的算法能够在低速范围内准确估计转子的速度和位置,比传统的高频注入方法更加准确,误差更小。
