一类广义Boussinesq方程局部弱解的存在唯一性

唐自敏，秦 敏，原子霞

（电子科技大学数学科学学院，成都 611731）

引言

经典的Boussinesq方程形式为：

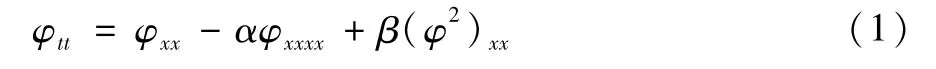
其中φ（x，t）表示流体自由表面的运动，α和β是常数，仅依赖于长波的特征速度和流体的深度。该方程用以描述潜水波表面小振幅长波的传播状态，由法国著名的数学家，物理学家 Boussinesq［1］首次提出。Barostichi与Figueira［2］得到了当 α=1时的方程（1），即“好”的Boussinesq方程，在Gevrey空间上解的适定性和全局正则性。Xue［3］研究了有界域上“好”Boussinesq方程的初边值问题。给出了该初边值问题的局部和全局适定性。

相对的，当 α=-1时，方程（1）被称为“坏”的Boussinesq方程。Yang和 Wang［4］对“坏”Boussinesq型方程初边值问题解的爆破问题进行了研究。随着对Boussinesq方程的广泛研究与应用，开始出现含有不同形式的非线性项的Boussinesq方程。方程φtt=φxx-αφxxxx+β（f（φ））xx被称为广义 Boussinesq方程。Linares和Scialom［5］研究了含有一个一般形式的非线性项的Boussinesq方程的初值问题

其中f（φ）=α-1φ，α＞1。此后，Dimova和Kolkovska［6］为分析孤立子轨道的稳定性与不稳定性，研究了具有两个非线性项的 Boussinesq方程 φtt=φxx-hφxxxx+（f（φ））xx，其中

f（φ）=aφ2+bφ3，h＞0，a，b∈ R，b＞0，a2+b2≠0。对于具有更一般的形式的两个非线性项的广义Boussinesq方程：

φtt=φxx-φxxxx+（aφp+1+bφ2p+1）xx，p＞0.Zhang［7］运用了Grillakis-Shatah-Strauss的轨道稳定性理论，得到了判断该方程孤波解的稳定性的一般性结论。此外，Lin、Wu和 Loxton［8］考虑了当f（φ）=-Δφ+ωφ时的情形，证明了在一定条件下问题（2）的解是爆破的。关于f（φ）被其它形式的非线性项所代替的情形具体可参看文献［9-11］。

在研究含有不同形式的非线性项的广义Boussinesq方程的基础上，具有高阶项的广义Boussinesq方程也开始被深入研究。Wang和Esfahani［12］在一维空间中研究了含有六阶项的Boussinesq方程的柯西问题

其中f（φ）=，β=±1。证明了该方程的解在中是全局适定的。基于Wang和Esfahani的研究，Geba与Witz［13］改进了六阶离焦全局适定性的Boussinesq方程，并推广了广义六阶Boussinesq方程φtt=φxx+βφxxxx+φxxxxxx+（f（φ））xx，其中f（φ）=φp。

本文将在三维空间下对高阶的广义Boussinesq方程进行研究

其中ΩT=Ω×［0，T］，μ=f（φ）=φ5-φ3+φ+Δ2φ-Δφ+6φ-6（φ2φ）-Δ5φ。这是一个新的数学模型，关于这个方程的研究不管是在数值计算还是理论分析方面都尚未报道。本文利用Galerkin方法证明Cauchy问题（3）局部弱解的存在性和唯一性。由于式（3）中关于梯度项的高度非线性的本质给理论分析带来了困难，借鉴Chen和Wang［14］的方法和技巧，本文将利用Sobolev空间理论克服这个困难。为简单起见，假设在 ∂Ω上，∂→n（▽iφ）=0，∂→n（▽iφ′）=0，i=（0，1，2，...，12）。

本文的主要结构如下：第1节介绍了一些基本不等式和主要定理。第2节对Galerkin逼近解进行了先验估计，利用这些估计在第3节证明了本文的主要定理。

1 主要定理

为证明本文中的主要定理，需要应用下面的基本不等式。

引理1（插值不等式）［14］如果r，k，j∈R，0≤k＜j＜r.那么，对任意的ψ∈Hr有下列不等式成立：

引理2（Gagliardo-Nirenberg-type插值不等式）［15］设j，m∈ N，q，r，θ∈ R，1≤q，r≤ ∞，≤ θ≤1，

如果 ψ∈Lq（Ω）∩Wm，r（Ω），那么 ψ∈Wj，p（Ω），且存在一个常数C=C（d，j，m，p，q，r，Ω）＞0使得下列不等式成立：

引理3（积分形式的 Gronwall不等式）［16］设 ξ（t）是［0，T］上的非负可积函数，对任意的t都满足下面的积分不等式

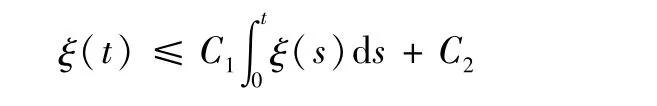
其中，常数C1，C2≥0。那么，对任意的0≤t≤T，ξ（t）≤C2（1+C1teC1t）。特别地，如果对任意的0≤t≤T都有

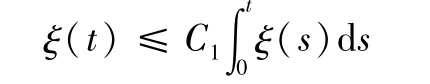
那么 ξ（t）=0。

下面给出问题（3）局部弱解的定义。

定义 1设 φ∈L∞（0，T*；H2），φ′∈L∞（0，T*；L2），φ′′∈L2（0，T*；H-1）。若对任意的v∈（Ω），存在一个正常数T*＞0，问题（3）在［0，T*］上存在唯一局部弱解 φ（x，t），当且仅当

（1）［φ″，v］+（▽μ，▽v）=0，

（2）φ（0）=φ，φ′（0）=ψ。

本文的主要定理是：

定理1问题（3）存在一个局部弱解。

定理2问题（3）的局部弱解是唯一的。

2 先验估计

2.1 Galerkin逼近解

引理4取逼近解的形式为：

（i）φm（0）=φ，

（ii）φ′m（0）=ψ，

（iii）（φ″m，wk）=（Δμm，wk）。

证明逼近解的形式由（4）给出，且wk=wk（x）（k=1，...）表示（Ω）中的标准正交基，于是有

令 （Δμm，wk）=fk（t），因此引理4中式（iii）的就转化为dk″m（t）=fk（t）。由常微分方程理论，对 ∀0≤t≤T（k=1，...，m），存在唯一的（t）满足方程组

从而存在唯一的逼近解φm满足方程

1.2 能量估计

用 · 表示空间L2中的范数，·p表示空间Lp中的范数，·Hs表示空间Hs中的范数。

命题1存在一个仅依赖于Ω，T的常数C，使得下列不等式成立：

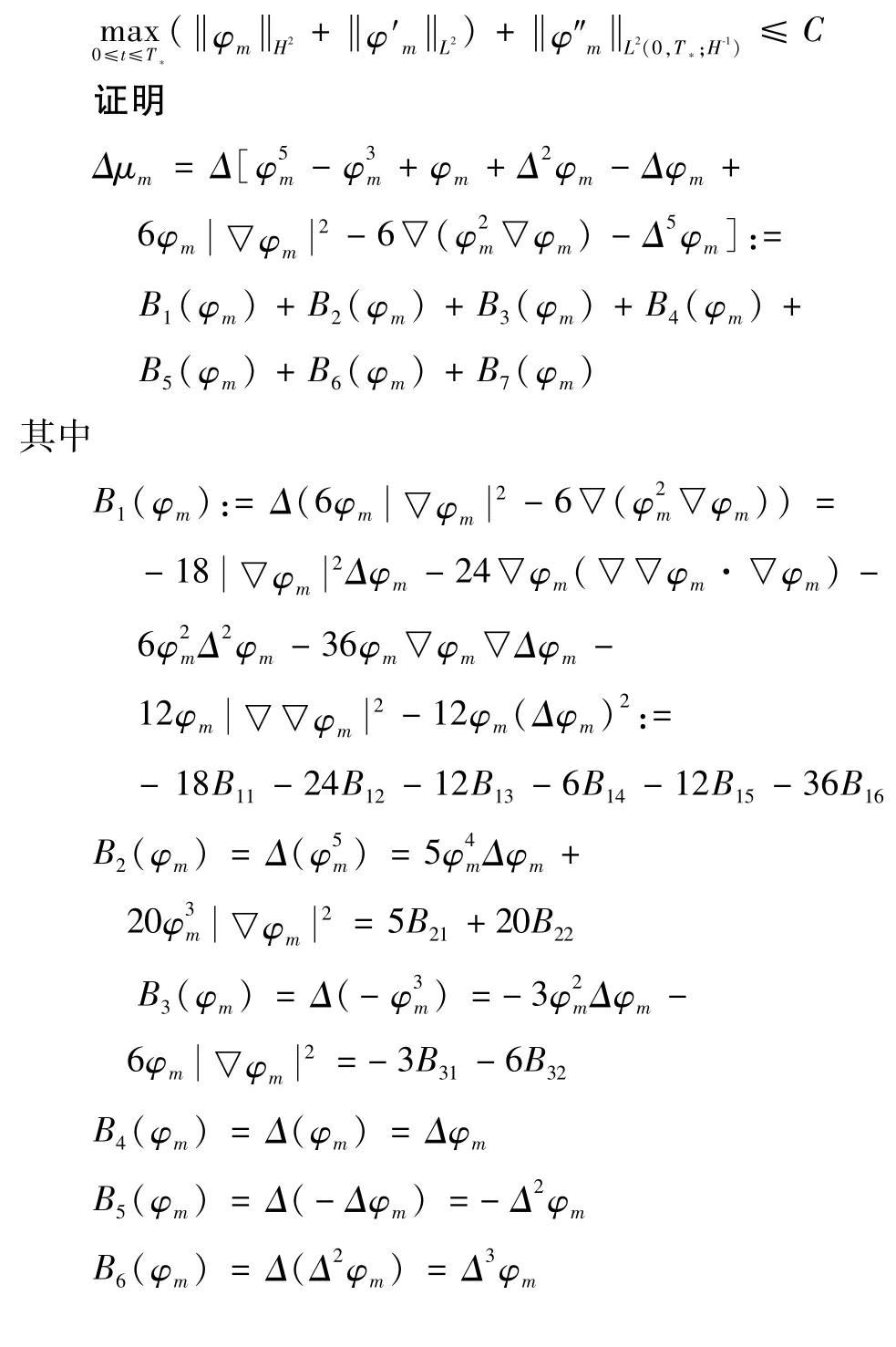
在引理4的式（iii）两边同乘 dk′m（t），并对k从1到m求和，则

把上述等式右端B5，B7与φ′m的内积移项到左端，因为

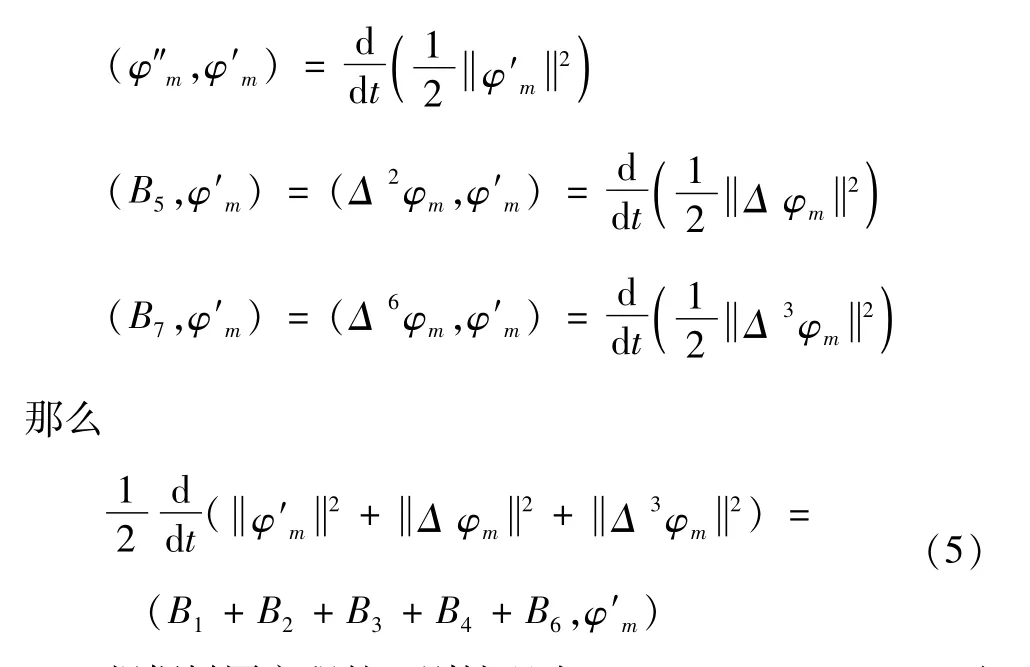
根据椭圆方程的正则性理论、Gagliardo-Nirenberg不等式和插值不等式可知

那么可以得到式（5）的估计式为

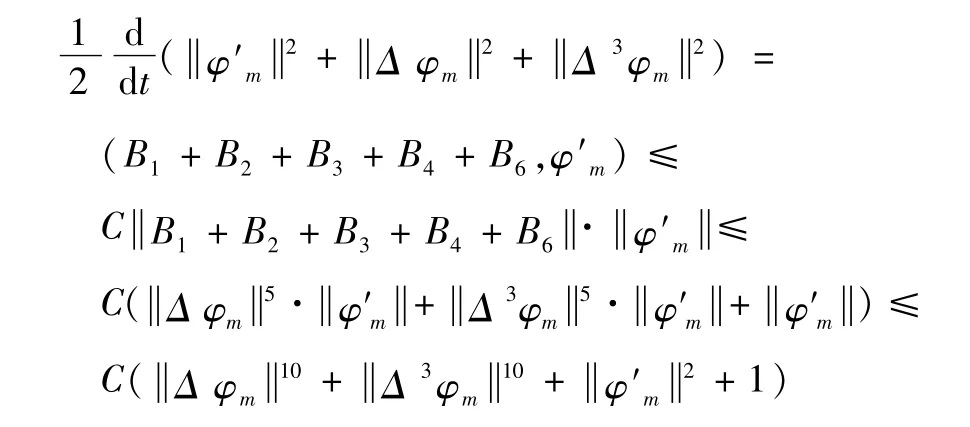
求解上述不等式得到

在引理 4的式（iii）两边同乘 Δ6dk′m（t），并对k从1到m求和，则

类似于前面对Bi的估计，由椭圆方程的正则性理论，Gagliardo-Nirenberg不等式、插值不等式和式（6）有

因此存在一个正常数T*，使得当Y2（t）≤C，0≤t≤T*时，有

由式（6）与式（7）可知

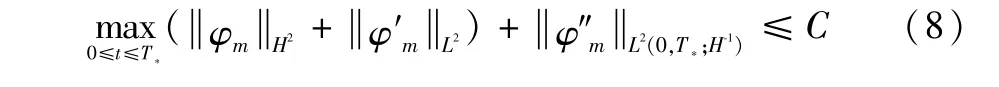
3 局部弱解的存在性和唯一性

本节证明本文主要定理，首先对定理1进行证明。

证明根据能量估计式（8）有：数列 ｛在L∞（0，T*；H2（Ω））中 有 界；｛在L∞（0，T*；L2（Ω））中 有 界；｛在L2（0，T*；H-1（Ω））中有界。

在L∞（0，T*；H2（Ω））中，φml弱收敛到φ，

在L∞（0，T*；L2（Ω））中，φ′ml弱收敛到 φ′，

在L2（0，T*；H-1（Ω））中，φ″ml弱收敛到 φ″。

φ″∈L2（0，T*；H-1（Ω））

任取正整数N和函数v∈C2（0，T*；H10（Ω））为如下的形式：

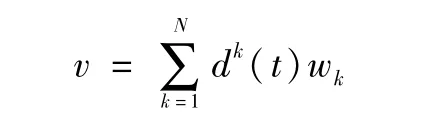
其中 ｛是光滑函数。任选m≥N，对引理4中式（iii）两边同乘dk（t），并对k从1到N求和，同时对t进行积分得到

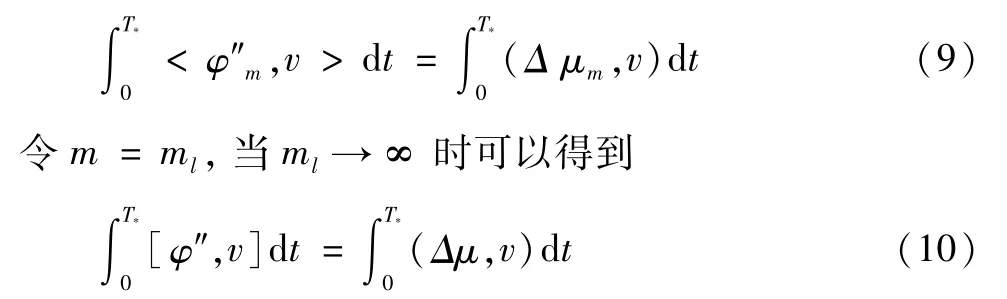
v∈L2（0，T*））是由wk表示的全体函数，

由稠密性可知对任意的v都有上述两式成立。

取v=ξ（t）·w（x），其中 ξ（t）∈L2（0，T*），w（x）∈（Ω）。则

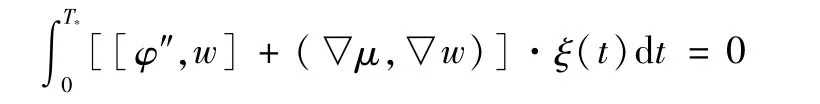
由 ξ（t）的任意性可知＜φ″，v＞+（▽μ，▽v）=0。

下面证明 φ（0）=φ，φ′（0）=ψ。

取函数v∈C2（0，T*；（Ω））且

v（T*）=v′（T*）=0。对式（10）进行两次分部积分，有

同样地，对式（9）进行两次分部积分

令m=ml，当ml→ ∞时，得到

由v（0）和v′（0）的任意性可知

φ（0）=φ，φ′（0）=ψ

定理1得证。

定理2的证明如下：

证明假设φ1和φ2是问题（3）的两个解，则φ=φ1-φ2满足方程

用φ′与φtt=Δ（μ）两端做内积，并把B4，B7与φ′的内积移到等式左端。因为

上式两端同时对t进行积分有

由积分形式的Gronwall不等式有

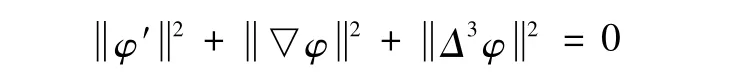
那么φ=0。定理2得证。