基于Laplace-Borel 变换的过程周期性操作的分析

苏 醒，翟 持

1.衢州学院，浙江衢州324000；

2.昆明理工大学化工学院，云南昆明650500

随着过程工业的深度集成与优化，化工过程的操作与控制呈现高度耦合的趋势，反应系统的非稳态操作成为最近的研究热点[1]。化工过程通常设计在定常态下运行，但有研究表明[2]，人为地使操作变量、反应物流向和加料位置等因素呈周期性变化，有可能改善反应器的时均性能。从非稳态操作的角度来看，外界周期操作或者内部不稳定性有可能变成过程强化的积极因素，如果对其加以恰当利用，不仅可以减少缓冲罐等单元设备的投资，还能取得更优的工程效果。

输入变量为参数的化工过程拟稳态曲线如图1所示。该过程描述发生在绝热、全混流反应器中的一个二级反应，模型方程如图1 右上角所示，其中：q为反应物流量，10 m3/h；k为反应速率常数，其值为1.2；V为反应器体积，100 m3。反应物的进料浓度为Cin，kg/m3；纵坐标目标函数为出口反应物浓度（y），其值越小表示转化率越高。由图1 可知，周期性地将操作点在A 和B 之间切换使出口平均反应物浓度平均值（yavg）小于y，即提高了反应物转化率。然而，分析周期性操作时还需要考虑反应的动态变化。Bittanti 等[3]根据变分原理给出了周期性操作强化过程的充分条件，并推导得到了π-判据。Parulekar等[4]运用π-判据研究了多输入扰动情况下的周期操作问题。因为π-判据将原系统线性化近似，所以对高度非线性系统，π-判据的分析结果只对小振幅的周期性输入有意义[5]。为了获得高阶非线性分析结果，Kravaris 等[6]采用中心流型理论对高度非线性过程的周期性操作进行了分析，该方法仅适用于渐进稳定系统的分析。Zuyev 等[7]使用非线性频域方法分析周期性操作，实现了过程强化的定量分析，但是该分析方法比较复杂，且对非周期相应分析效果不佳。

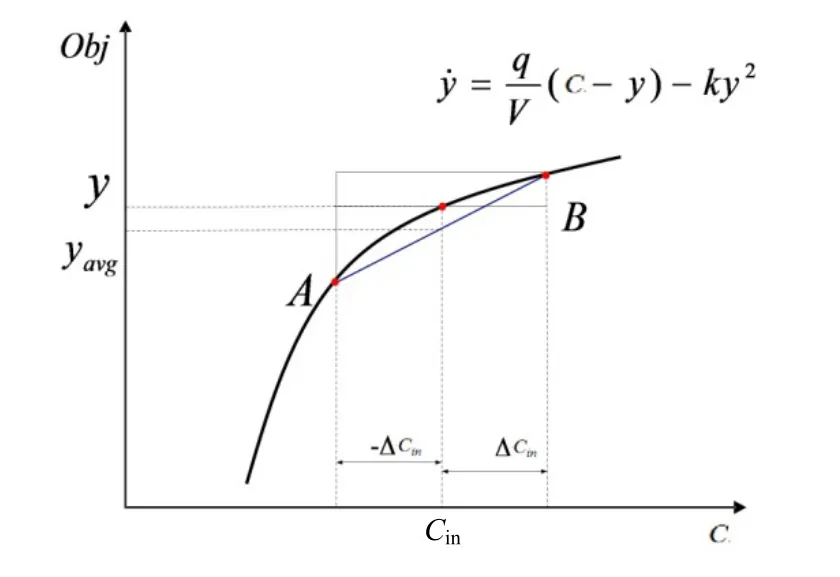
图1 输入变量为参数的化工过程拟稳态曲线Fig.1Steady-state cerve for a process system

本工作以Laplace 变化为基础，利用Borel 展开分析非线性过程的周期性操作问题，以期有效地分析单扰动和多扰动周期操作问题。基于Laplace-Borel（LB）变换实现高度非线性系统的高阶解析近似[8]，通过引入积分算子，非线性动态系统可以描述成一个无穷级数的泛函形式，并且满足Shuffle操作。鉴于过程系统引入多个周期性输入时，输入参数间的关联以及输入与系统间的耦合使研究系统变得极为复杂，分别以单输入和多输入周期性操作为例，介绍基于LB 变换的周期性操作的分析方法。

1 周期性操作的分析理论

一个连续的非线性动态过程的最优周期性问题可描述如下：

其中：x∈Rn，是过程系统的n维状态变量；u∈Rm，是系统的m维周期性输入；φ和ψ分别为系统的等式、不等式约束条件。最优周期操作就是寻找到合适的周期性输入u，使目标函数J最大化。

1.1 非线性传递函数

引入LB 变换以及相应的Shuffle 运算，将式（1）所述的最优周期性操作问题映射到复变函数域，形成非线性传递函数。当系统由多个微分方程组成，LB 变换可以实现变量间的分步解耦[9]。现对一维的常微分方程进行LB 变换，类似地可推广到多维系统。

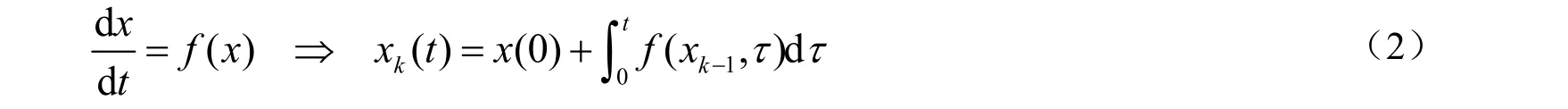
其中：f(x)是一个连续方程。式（2）可进一步写成通式：

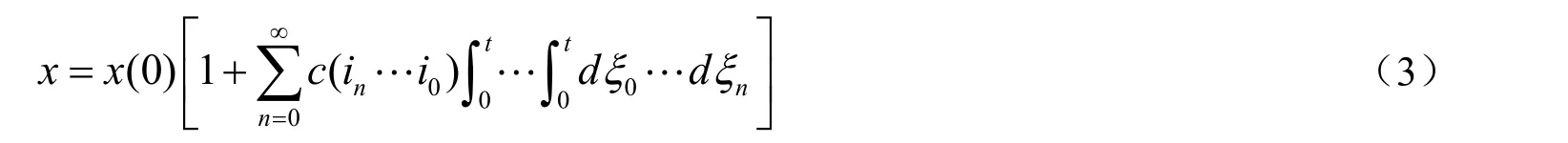
其中：ξ0…ξn为嵌套积分的积分时间，Ц 为Shuffle 运算符，通过x0-域变换将式（1）转化为代数运算，实现非线性传递函数构建。

与Laplace 变换相似，LB 变换将常微分方程（ODEs）映射到x0域，从而得到代数方程组，通过Shuffle运算将系统解耦成独立的方程，然后逆LB 变换即得到时域解。由于非线性方程通过LB 变换得到的是无穷级数，所以运用LB 变换得到的解是近似解。常微分方程通过Taylor 展开可以得到如下形式：

进而定义LB 变换，如式（6）所示。常见的初等函数的LB 表达式见表1，a和b为常量，F(x0)为象，f(t)为原象。

表1 典型初等函数LB 变换Table 1LB transform of some functions

1.2 基于LB 变换的泛函展开

当系统为多个ODEs 时，Picard 迭代积分不能保证收敛，因此，运用泛函展开[11]近似求解ODEs时的收敛问题。对一个多维系统，如式（7）所示：

其中：x∈Rn，u∈Rm，A∈Rn*n，B∈Rn*m，ξ(x,u)是多项式型的函数向量。式（7）LB 变换成式（8）：

其中：XL与XN分别为线性和非线性部分的函数。

由于出现Shuffle 算子，式（8）中的X不能显式给出，因此将其泛函展开：X=XL+XN(1)+XN(2)...，相应地，其非线性部分XN就能逐次展开。与Laplace变换类似，LB 变换能对非线性系统进行频域分析。本工作重点讨论输入为余弦变化时，系统的动态响应特征，进而研究周期性操作问题。为方便理解，将泛函展开描述为输入-输出型的框图形式，如图2所示。其中，XL为式（8）定义的线性传递函数，L 为Laplace 变换，fi为如下形式：

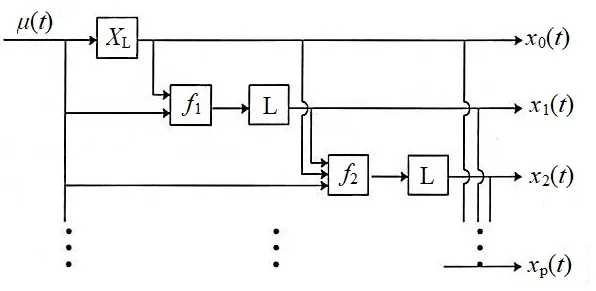
图2 输入与输出型的泛函展开框图Fig.2Block diagram of the functional expansion

将式（10）带入（8）的泛函展开，可以实现周期性操作的分析。

2 单输入周期性操作问题

2.1 乙醇发酵-膜分离耦合过程

工业上常用运动发酵单胞菌（Zymomonasmobilis）或酿酒酵母（Saccharomycescerevisiae）发酵生产乙醇，但是乙醇是二次代谢产物，随着发酵罐内产物的累积，微生物生产乙醇过程会被抑制，甚至使微生物失活，因此，当前的研究热点是采用原位产物移除技术及时移走发酵过程产生的乙醇。为研究产物抑制的时间滞后问题，Jobses等[11]建立了结构化模型，将生物质分为关键组分K和其余部分G，其中，只有当前时刻系统中K 的含量能决定下一时刻生物质的生成量。结构化模型区别于传统的基质-生物质-产物（s-x-p）模型，需要增加K 关键组分（e），形成如式（11）所示的四维模型。

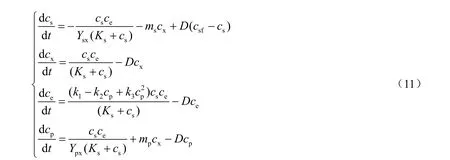
其中；cs，cx，ce和cp分别为发酵罐内基质、生物质和关键组分及产物的浓度，kg/m3；D为稀释速率，h-1；ms为维持微生物生长常数，kg/(kg·h)；csf为输入底物浓度，kg/m3；ks为饱和常数，其值为0.5 kg/m3；Ysx和Ypx分别是基于基质和产品的屈服因子，其值分别为0.024 449 8 kg/kg和0.052 631 5 kg/kg；k1，k2和k3为经验常数，其值分别为16 h-1，0.497 m3/(kg·h)和0.003 83 m6/(kg2·h)。

为消除乙醇抑制作用，根据渗透膜的选择性透过性能，设计了如图3 所示的乙醇发酵-膜分离耦合发酵过程。膜组件右侧使用吹扫蒸汽携带走乙醇产品，使发酵罐内的乙醇含量不足以抑制发酵过程。发酵罐转移的乙醇通量为：

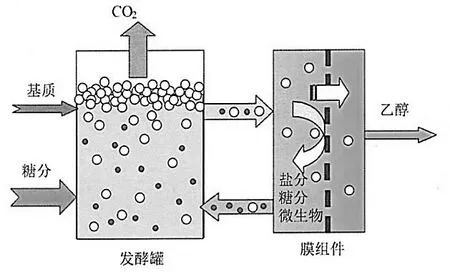
图3 乙醇的膜发酵过程Fig.3 The membrane fermentation process

式中：cp和cpM分别为发酵侧及渗透侧的产物浓度，kg/m3；F为膜的乙醇渗透性能，为0.128 3 m/h；AM是膜的面积，m2；VF为发酵侧的体积，为0.003 m3。

图4 膜生物发酵过程。如图4 所示，由于存在膜的渗透作用，进入发酵侧的稀释速率D与出发酵侧的不再相同，分别用Din和Dout表示进、出发酵侧的稀释速率，h-1；同样地，用分别用DMin和DMout表示吹扫蒸汽进和出渗透侧的稀释速率，h-1。乙醇发酵-膜分离耦合发酵过程的动态模型可写成：

图4 膜生物发酵过程Fig.4The membrane fermentation process

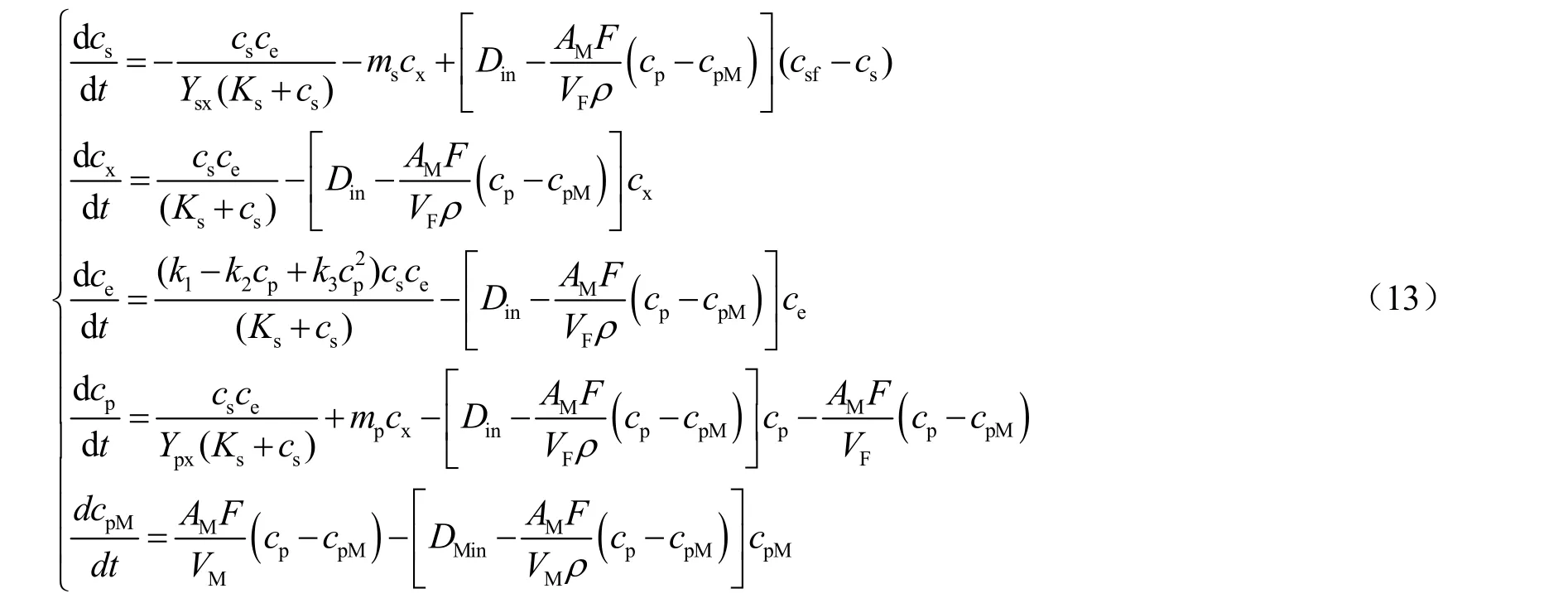
式中：VM为渗透侧的体积，为0.000 3 m3；ρ为乙醇的密度，其值为789 kg/m3。

2.2 周期变化吹扫蒸汽稀释速率的膜分离过程分析

研究发现，当输入底物浓度（csf）为140 kg/m3且发酵侧的输入稀释率为0.022 h-1时，发酵罐内累积的乙醇已经对发酵过程产生明显的抑制作用，并且形成自振荡。若设计膜面积为0.24 m2，吹扫蒸汽稀释速率为0.5 h-1时，系统不会形成自振荡并且趋向稳定。相比于没有膜分离的过程，耦合膜分离过程的乙醇产率提高了8.6%。然而，蒸汽渗透膜存在堵塞和污染等问题，通过周期性改变吹扫蒸汽速率，让膜表面得到更新，减小膜堵塞的影响。周期操作的目标是强化生物质的乙醇产率（rp），其数学表达式为：

式中，rp为图4 所示的两股出料中乙醇质量流率在τ周期的时间平均值，kg/h。当膜组件的AM为0.24m2，DMin为0.5 h-1条件下，稳态操作时的rp为4.590×10-3kg/h。

如果DMin引入余弦变化：δDMin=Amcos(ωt+φ)，由于是单变量周期性操作，可忽略相位角（φ）的影响，将其LB 变换后得到式（10）。结合式（11）和式（12）建立发酵-膜分离耦合模型，LB 变换后得到式（15）：

其中：BL[x]∈Rn*n，BL[u]∈Rn，为多项式B[x,u]的线性部分；x(0)=0，是稳态工作点为原点的初值；A0是多项式A[x]的雅克比矩阵。

根据式（15）可以获得x0域动态过程的泛函展开：

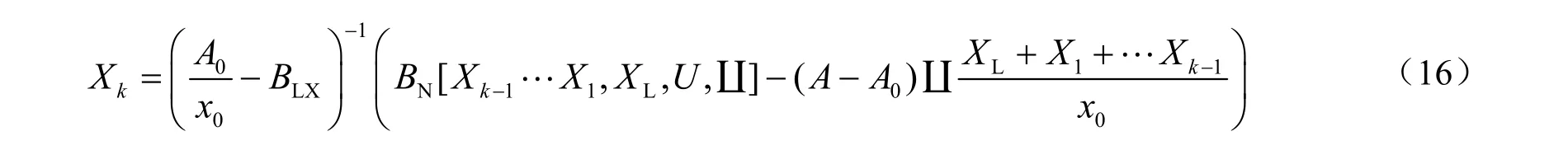
其中线性部分（零阶泛函展开）可写成：

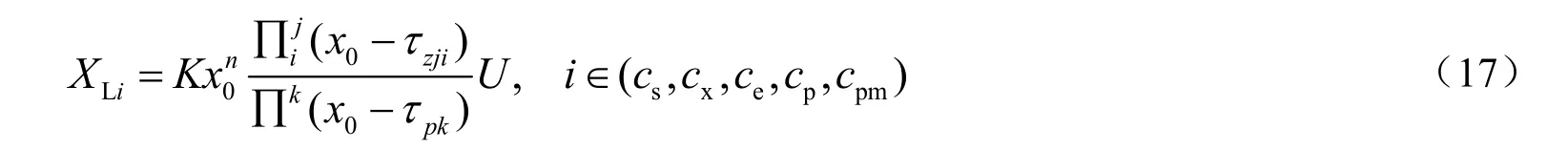
式中：τz和τp分别是LB 变换的零点和极点。根据图2 进行Shuffle 运算，可得到高阶的泛函展开。

图5 给出过程的一阶泛函展开，其中自变量为方程式（10）所述的扰动频率和振幅。由图5 可知，通过对吹扫蒸汽DMin进行余弦变化，该发酵-膜分离系统的乙醇产率得到增强，这种增强效果随着振幅的增加而增加，而随着频率的变化，一阶偏差影响不大。因此，可以采用工程上容易实现的变频方式周期性改变DMin，应尽可能增加周期操作的振幅，来实现对该过程的强化。

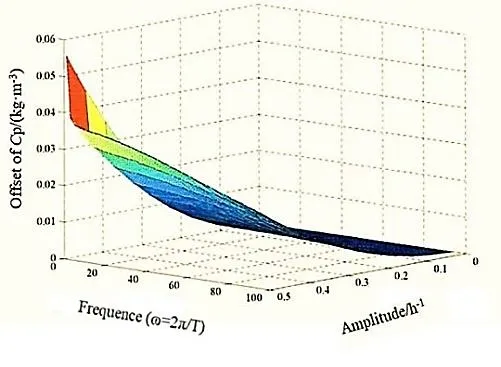
图5 乙醇在发酵侧的偏移（一阶泛函展开）Fig.5The offset of the ethanol in the fermentation side

3 多输入周期性操作问题

3.1 串联-平行反应过程

基于LB 变换可以方便地实现多输入扰动的分析。区别于单输入周期性操作，多输入时，相位角偏差（φi-φj）是一个重要的操作变量，因此，多输入周期性操作问题的分析因素较多。在串联-平行反应中，关注的核心是中间产物的产量最大化，同时产生尽量少的副产物。考虑一个在绝热的连续全混流反应器（CSTR）中发生的反应：

其中：k1 和k2 分别为两个基元反应的反应速率常数。可以建立系统的动态方程：

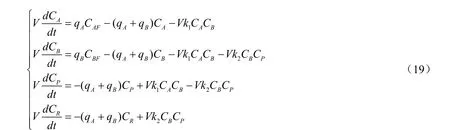
其中：V为反应体积，m3；CAF和CBF为A 和B 的进料浓度kmol/ m3；qA和qB为原料A 和B 的体积流率，m3/h。该体系的目标是产物P 的时均产量最大化，同时考虑副产物R 分离成本及原料A和B 的成本：

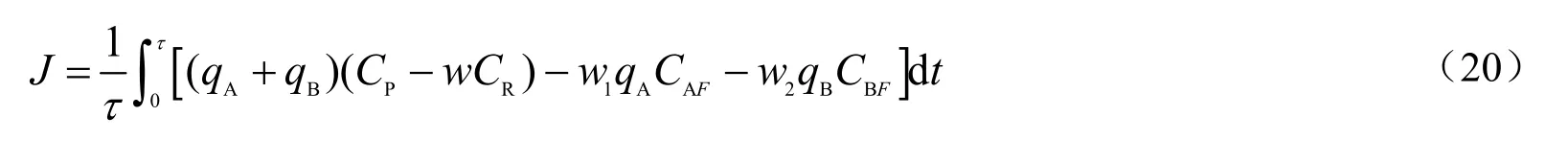
式中：J为反应体系的总收益的评价指标；w为副产物R 分离成本相对于目标产物权重；w1与w2分别为原料A 和B 的成本相对于目标产物的权重。

3.2 稳态操作

当系统稳态时，目标产物最大化仅与两个反应进度（ηi）有关：

式中：J0为稳态时产物P 产量最大化函数；FA0为反应物A 的初始摩尔流率，kmol/h；θB为B 与A 摩尔流率之比。通过解析分析得到各组分的稳态浓度如下：

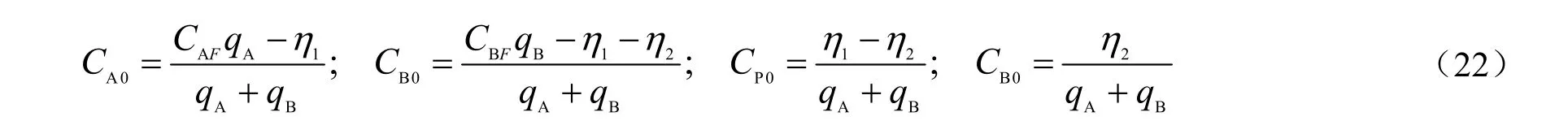
假设式中w1，w2，FAF及FBF恒定，令x=η1FA0，可推出J0最大条件及状态（∂J0/∂x=0，∂2J0/∂x2<0）。

当不考虑副产物R 的分离成本，w为0，并且两个反应常数之比（ζ=k2/k1）为0.1 时，可得xmax为0.759 747，ym=η2FA0，其值为0.182 532。取1/θB为0.82、稀释率（dA=qA/V）为0.1 h-1，k1为1。对应的各物质的稳态解为：CA0为0.327 0 kmol/m3，CB0为0.123 8 kmol/m3，CP0为0.208 3 kmol/m3。

3.3 多输入的周期性操作

现讨论反应物A和B的浓度周期性变化对系统的影响。余弦扰动U1和U2的LB 变换分别为：

其中：ω1和ω2为两个扰动的角速度，rad/h；θ为两个扰动U1和U2的相位移差，h-1；Am1和Am2为振幅，kmol/m3。为方便分析，取：ω1=ω2=ω，将式（19）进行LB 变换，并带入（24）得：

通过变量解耦及消去瞬态项得到线性项的解满足如下形式：

由以上参数得到：τp1=0.7150，τp2=0.3139，τp3=0.1976。τXi分别为不同变量的一阶项零点。由此可得一阶余项为：A

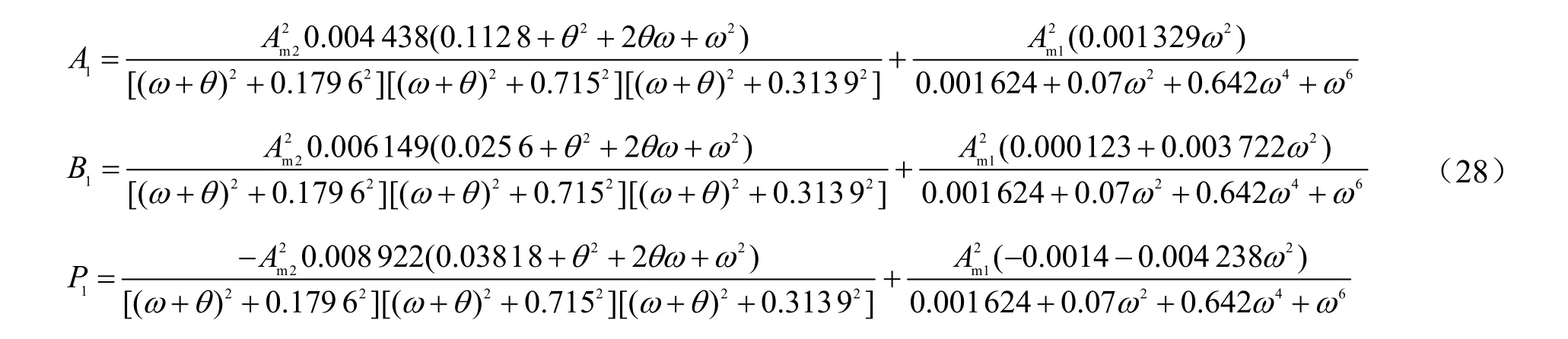
由上式可知，系统泛函序列取一阶非线性展开会生成余项，发生对称破裂分岔。该系统非线性部分是无记忆算子，运用LB 转换的泛函序列具有收敛性质，截取的泛函展开项越多，计算结果就越趋近真实解。

当不考虑副产物分离，即w为0，周期性操作仅改变式（19）产物P 的时均值，两个角位移对P的时均值的影响如图6 所示。

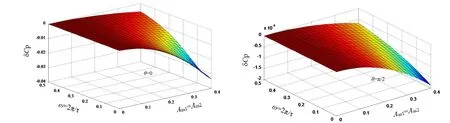
图6 产物P 的一阶余项随频率和振幅变化关系Fig.6The first order offset of product Pconcentration with varying forcing amplitude and frequency

由图6 可知，当系统处于最优稳态运行附近，对反应物A 和B 的浓度实施周期性操作会导致产物P 的浓度减小，性能函数随着振幅的增加、频率的降低而恶化，并且θ为0 时的恶化程度高过θ为π/2 时的。该案例也说明，不是所有的非线性系统都适合采用周期性操作的方法实现过程强化。

4 结 论

本工作使用LB 传递函数研究连续乙醇发酵-膜分离系统，串联-平行反应过程的解析近似解，在此基础上讨论了多波动参数的周期型操作对系统性能函数的影响。LB 变换是一个非线性传变换，将原问题转换成一系列泛函展开，通过Shuffle 运算，实现系统的分部解耦。本工作提出的方法也可以用来研究参数对非线性过程敏感性的问题，对后续过程控制及操作提供相关的信息。