速度300 km/h列车振动荷载下隧道衬砌加速度响应规律分析
2020-07-13黎国清齐法琳
田 甜,黎国清,齐法琳,董 军
(1.中国铁道科学研究院集团有限公司,北京 100081;2.北京建筑大学 工程结构与新材料北京市高等学校工程研究中心,北京 100044)
随着我国经济的腾飞与科技发展,人们对出行的要求日益提高,高速铁路以快速、准时、安全可靠等特点,成为了现代人城市间出行的重要手段。列车在高速行驶过程中产生的车体振动将会直接作用于高速铁路隧道及其背后围岩,隧道结构及其背后岩体对列车振动的响应将会对隧道结构稳定造成一定影响,这也成为了铁路行业极为关注的问题之一。在隧道现场进行测试试验是取得隧道振动响应最直观、直接且有效的方法,其结果不仅能够为相应的理论研究提供依据,也可以用来验证理论计算模型与数值模型的正确性。但是因为高速铁路运营的客观条件制约,这方面的研究,尤其是针对高速铁路隧道现场振动响应测试的实测研究鲜有涉及。
对于隧道在列车荷载作用下的振动问题,许多专家学者开展了不同角度的试验研究。文献[1]通过现场试验得到了低速列车振动荷载谱。文献[2-3]通过对隧道仰拱和边墙在列车荷载作用下动力响应的研究和试验,得到了车速越高对隧道仰拱和边墙动力响应影响越大的结论。文献[4-5]对70 km/h速度列车通过隧道进行了现场试验,获得部分控制点的动态响应状态。文献[6-9]针对隧道衬砌在列车竖向荷载作用下的状态进行了研究。文献[10-12]针对隧道频响特性进行了分析与研究。以上研究的对象大部分为地铁和普速铁路隧道,对于高速铁路隧道在列车荷载作用下的动力响应试验及研究未有涉及。
为丰富我国高速铁路隧道衬砌动力响应研究,并为隧道衬砌振动响应数值模型计算提供现场测试数据,本文选择国内某高速铁路隧道进行现场测试,对列车以300 km/h速度通过隧道时引起的衬砌拱圈动力加速度响应传递规律进行一定分析,开展理论模型数值计算与试验数据对比研究,提出了隧道衬砌在速度300 km/h列车荷载作用下拱圈横向和竖向动力加速度响应传递规律,拟合了拱圈加速度响应传递经验公式,以期揭示高速铁路隧道在列车荷载作用下振动响应传递的一些内在机制,为今后的研究提供有利的试验和模型参数基础。
1 速度300 km/h高速铁路隧道现场振动测试试验
试验现场选择我国某高速铁路隧道,隧道建筑轮廓见图1。
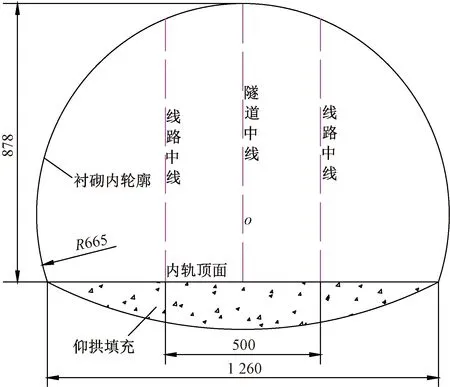
图1 某高速铁路隧道建筑轮廓(单位:mm)

图2 A点传感器布置
试验过程中,考虑到设备运输,振动采集设备电池及时更换、数据及时存储与分析,选择在距离隧道洞口500 m处的浅埋区隧道断面位置进行传感器布置。在隧道断面位置与左线钢轨交点正下方,轨道板上安装布置测点A,测试点A的高度取为0 m,目的是当列车接近时与被测断面相距约200 m触发采集系统信号,并同时采集此位置列车振动引起的轨道板竖向振动加速度,振动加速度传感器选用INV9828型,最大量程设置为10g,见图2。
隧道衬砌内表面传感器设计及布置受到现场客观条件限制,出于对高速列车行车安全的考虑,衬砌测试点高度选择在一定的安全范围内,只在隧道衬砌内表面左线一侧每间隔1 m位置布置一处横向及竖向传感器,总测点数为6处,其中测点1与轨道板测点A处于同一水平面,高度为0 m,依次类推得到测点2~6的高度分别为1、2、3、4、5 m(图3)。同样选用INV9828型振动传感器,最大量程设为5g。每个测点处同时布置横向与竖向加速度传感器,其中竖向传感器垂直于轨道水平面,横向传感器与轨道水平面平行并用螺栓固定于铝合金正方体支座,传感器支座固定在衬砌表面的三角钢支架上,见图4。
为了消除采集过程中隧道环境及行车过程的干扰因素,并从保证列车行车安全角度出发,将测试系统采集设备安置于配电箱内,并用电池供电(图5)。
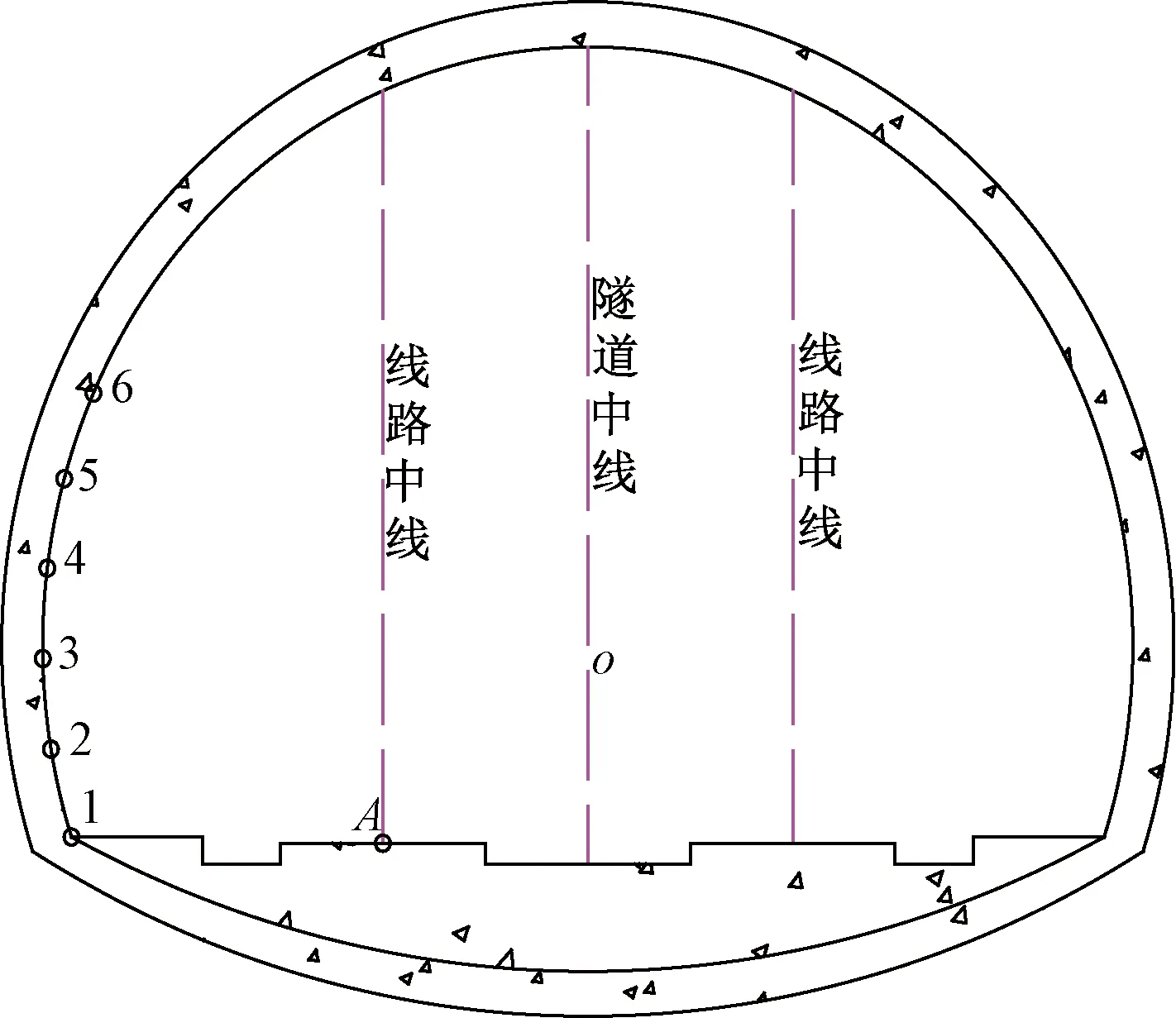
图3 传感器测点现场布置图

图4 竖向、横向传感器设计及布置

图5 配电箱及电池布置
2 测试结果及分析
2.1 隧道现场测试结果
通过本次试验,分别测试得到2组高速铁路列车以300 km/h沿右线上行方向(以下简称右线方向)和6组高速铁路列车以速度300 km/h沿左线下行方向(以下简称左线方向)经过隧道断面时的现场实测数据。当列车沿左侧线路通过隧道测试断面时,此时列车位于接近测试点一侧。
采集系统交流震荡波未能完全滤波,造成位于衬砌高度为4 m处的测点5数据异常,所以在数据分析过程中不考虑测点5。
图6为墙角处竖向和横向加速度时程曲线。

图6 墙角处加速度时程曲线
列车以300 km/h车速沿左线通过隧道测试断面时,衬砌各测试点位置竖向振动加速度与横向振动加速度峰值关系对比曲线,见图7、图8。
与上述计算处理和计算方式相同,右线列车通过隧道测试断面时,其加速度峰值关系曲线见图9和图10。
图11、图12分别为列车以300 km/h速度沿右线或左线方向行驶时,隧道衬砌各位置测试点竖向加速度与横向加速度峰值均值响应关系曲线。
2.2 衬砌在列车荷载作用下加速度响应分析
2.1节对试验采集数据进行了处理和计算,绘制了衬砌响应加速度变化曲线,对比分析各响应加速度曲线可知,当列车沿远离隧道测点一侧线路(右线)通过时(图9),衬砌加速度响应明显小于列车沿接近隧道测点一侧线路(左线)通过的衬砌加速度响应(图7、图8),即当列车通过隧道时,距离列车越远,列车荷载振动对衬砌加速度响应影响越小,隧道衬砌响应加速度值越小。
对衬砌竖向加速度响应(图7、图9)分析可知:
(1)隧道墙角高度为0位置(测点1)加速度响应均为列车通过时衬砌加速度响应最大值,列车远近仅影响衬砌竖向加速度响应相对值大小。
(2)衬砌竖向加速度响应在墙角出现最大值,列车与测点的距离对这一趋势没有影响,仅影响各测点数值大小。
(3)当列车接近衬砌测点位置通过时,衬砌各测试点竖向加速度响应在不同时刻所得数据离散度较高,但当列车距离测点较远时,各测点位置不同时刻衬砌竖向加速度响应所得数据误差较小。
(4)当列车沿远离列车一侧线路通过隧道相对沿近车一侧线路通过时,隧道衬砌竖向加速度响应随高度的增加下降趋势明显较快,说明距离列车激振源越远,衬砌加速度响应传递衰减越明显。
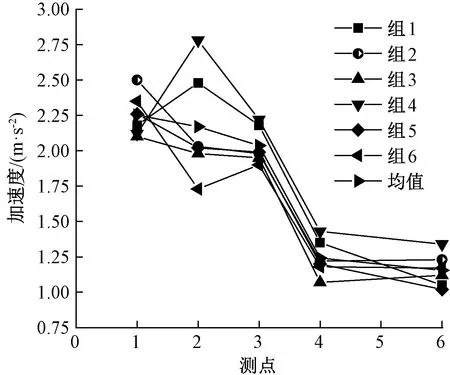
图7 列车沿左线通过时衬砌竖向加速度变化曲线

图8 列车沿左线通过时衬砌横向加速度变化曲线

图9 列车沿右线通过时衬砌竖向加速度变化曲线
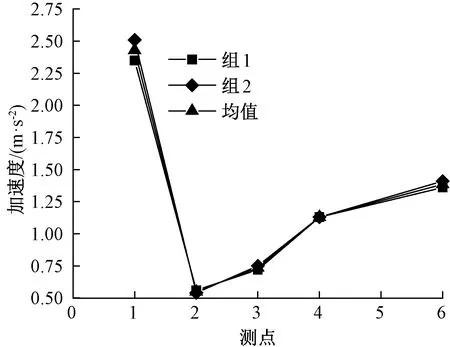
图10 列车沿右线通过时衬砌横向加速度变化曲线
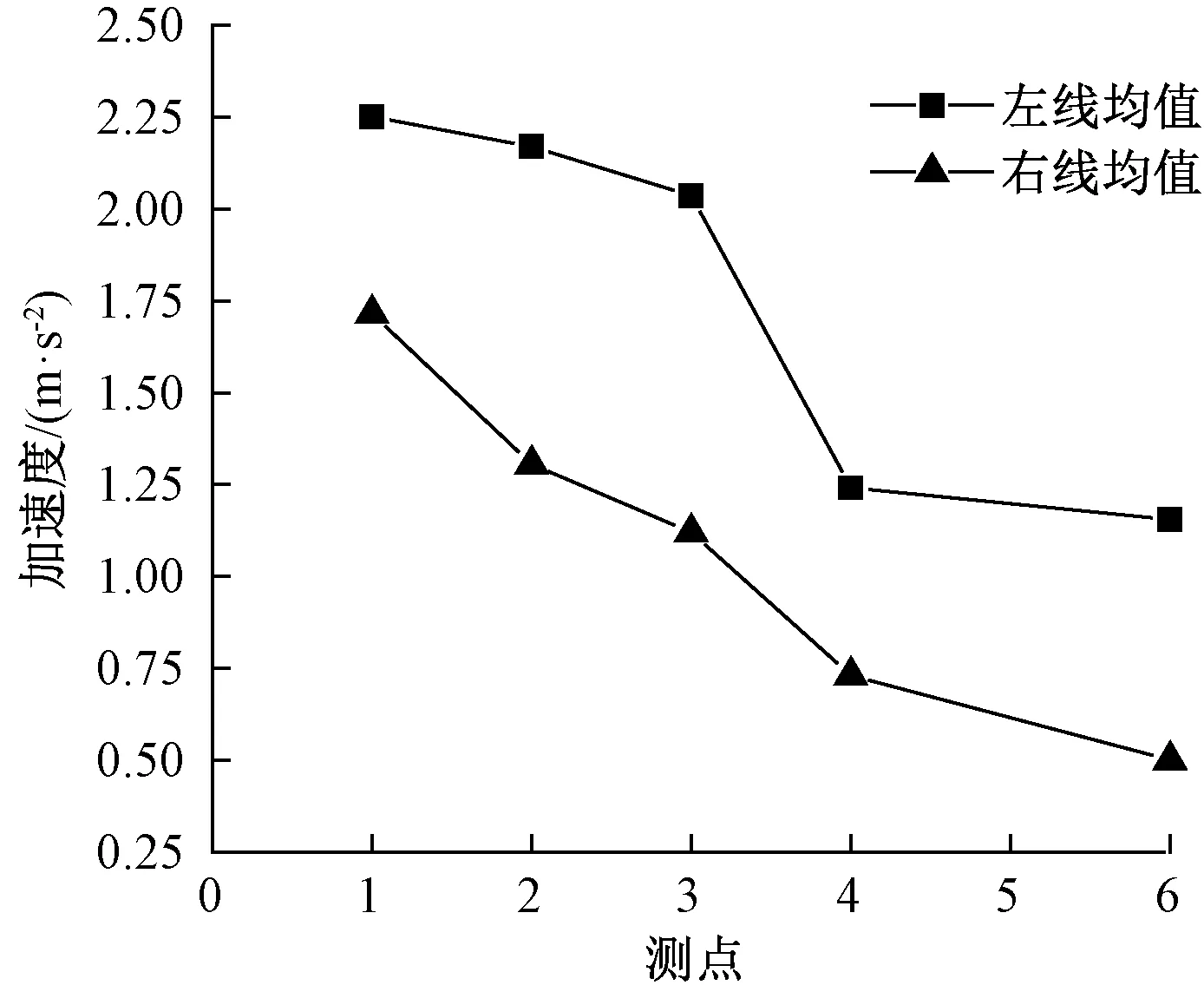
图11 不同行别列车竖向加速度均值变化曲线
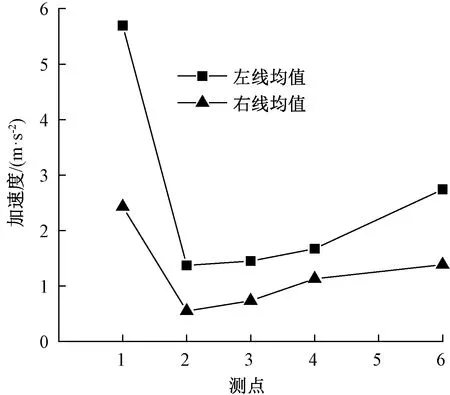
图12 不同行别列车横向加速度变化曲线
对衬砌横向加速度响应(图8、图10)分析可知:
(1)隧道墙角高度为0位置(测点1)横向加速度响应均为列车通过时出现(测点1)最大值,而后在高度1 m处的测点2突然降低至最低,之后随隧道衬砌测点高度的增加,横向加速度响应值呈逐渐增大趋势,列车远近仅影响衬砌横向加速度响应相对值大小。
(2)列车远近对衬砌横向加速度相对值影响较大,尤其在墙角位置,衬砌近车一侧相比远车一侧出现数倍差距,由此可知列车距离对衬砌的横向加速度响应影响比较显著。
(3)由图8和图10分析可知,衬砌横向振动响应加速度在接近列车或远离列车时,均不具备较高的离散性。
(4)与竖向加速度不同,衬砌横向加速度响应不具有明显的线性趋势,而且左线与右线横向加速度变化趋势相同。
2.3 隧道衬砌加速度响应频谱分析
对隧道现场列车沿左线通过时各测点的衬砌加速度进行分析,提取各测点竖向和横向加速度频谱,见图13~图20。
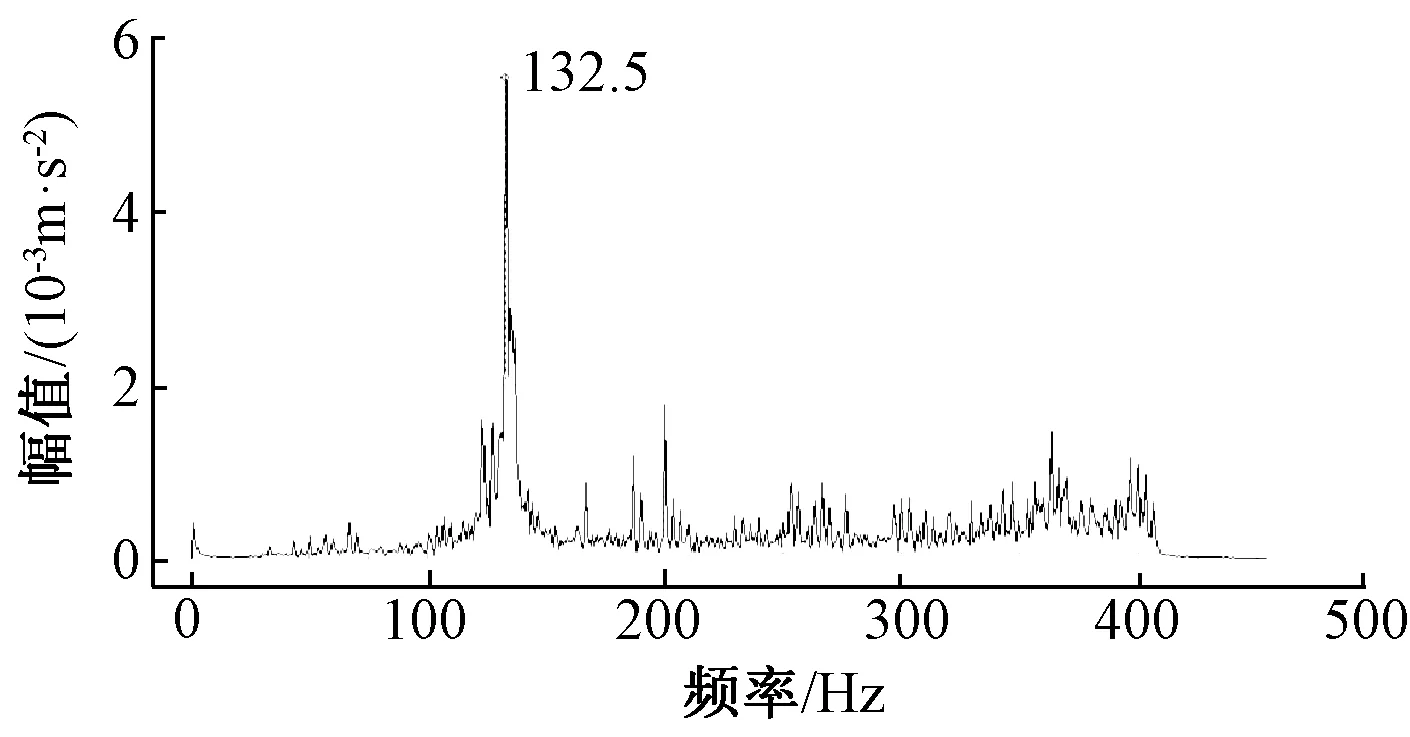
图13 测点2横向加速度频谱
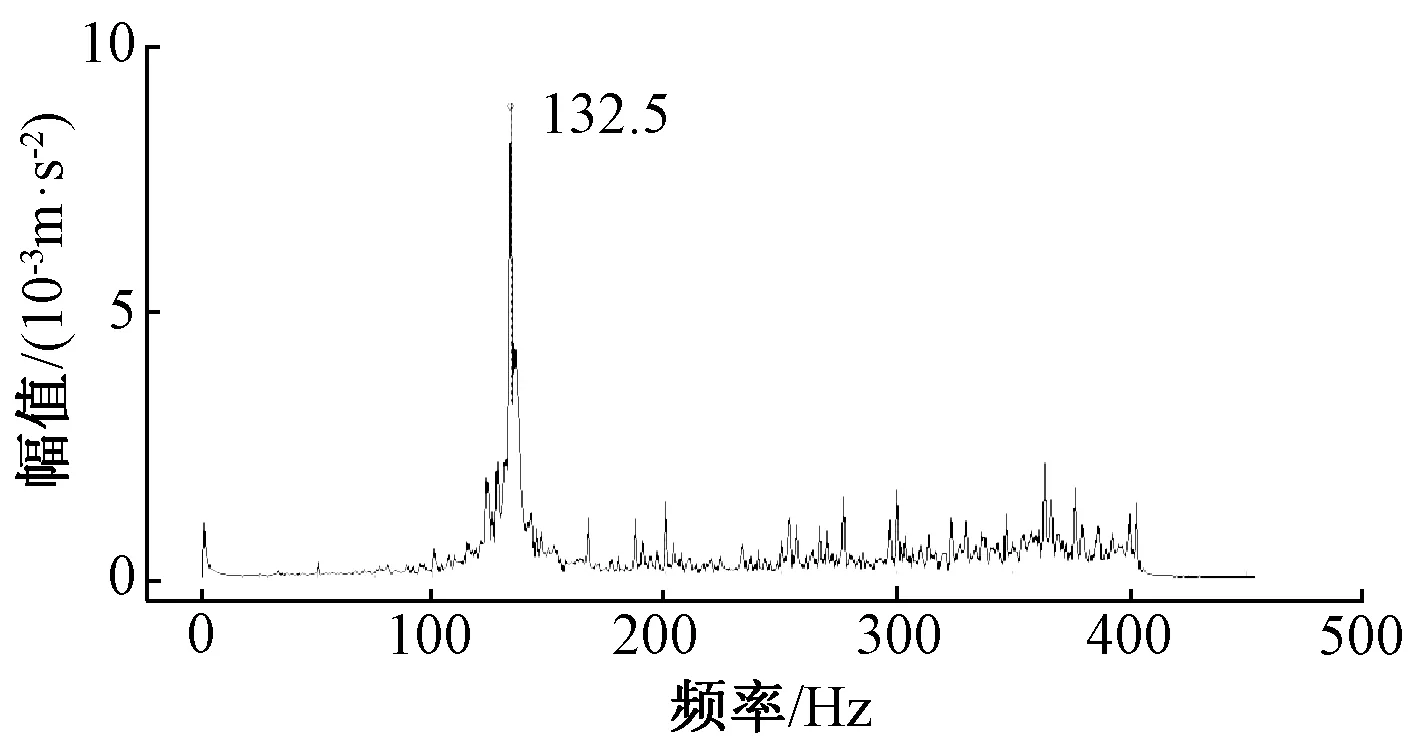
图14 测点2竖向加速度频谱
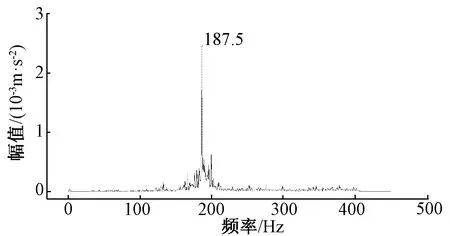
图15 测点3横向加速度频谱
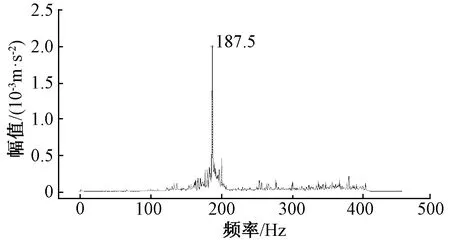
图16 测点3竖向加速度频谱
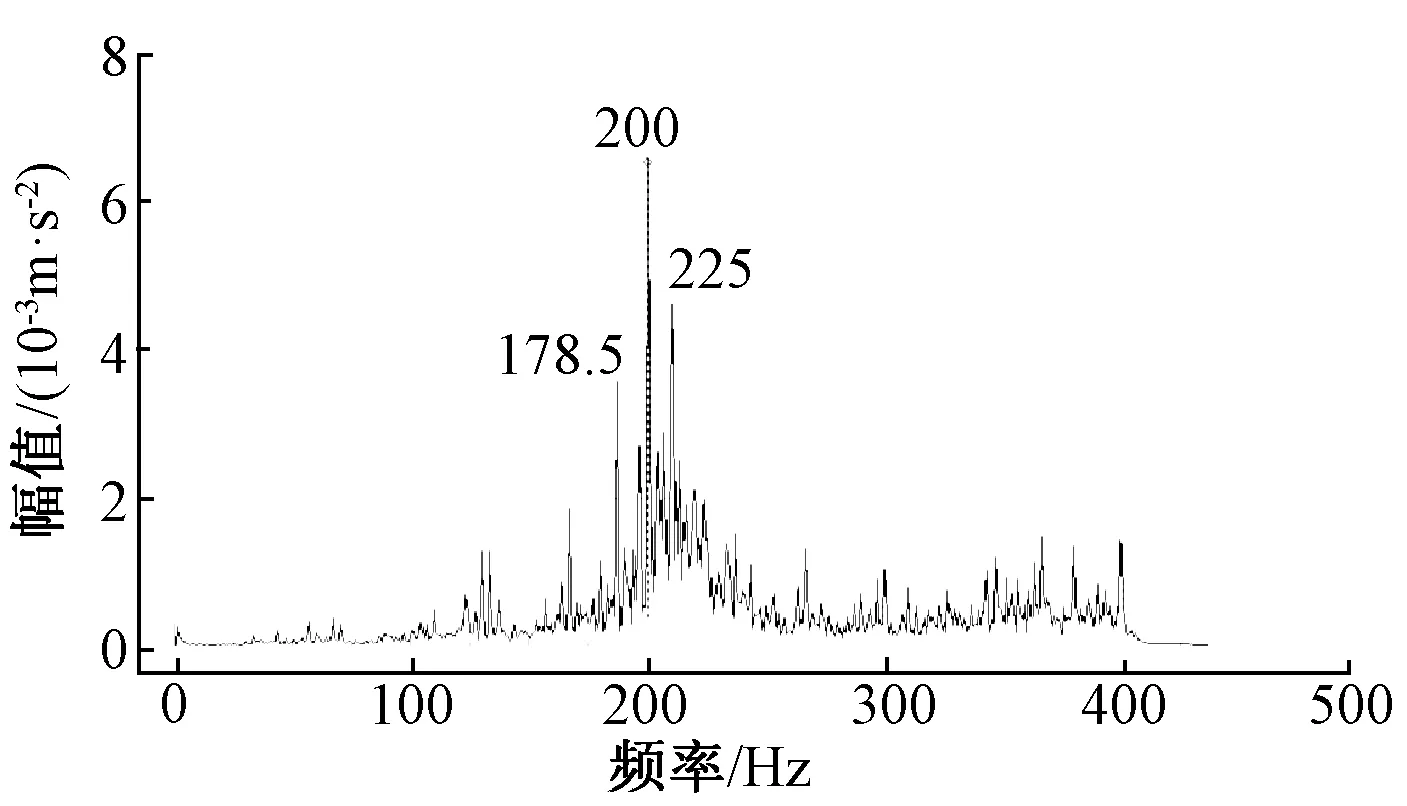
图17 测点4横向加速度频谱

图18 测点4竖向加速度频谱
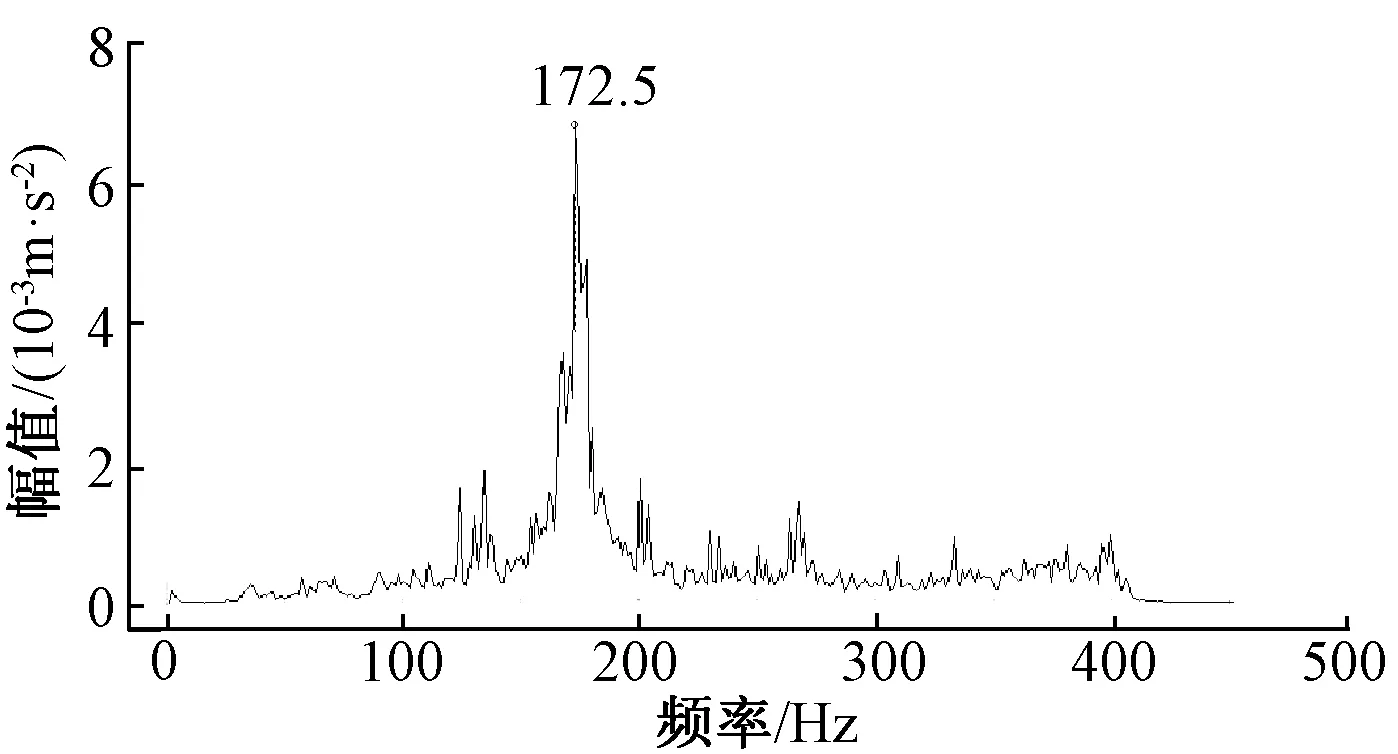
图19 测点6横向加速度频谱
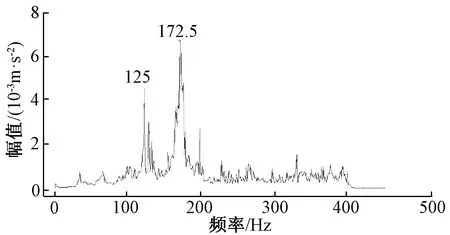
图20 测点6竖向加速度频谱
对列车沿左线通过隧道衬砌断面时衬砌各测点竖向与横向加速度频谱波形进行分析,可知衬砌测点2和测点3处的横向与竖向加速度响应频谱波形均呈现出单峰值趋势,其中测点2位置处的峰值频率为132.5 Hz,测点3位置处的峰值频率为187.5 Hz,两个测点位置均存在一定的高频作用但激励较弱,而低频激励不明显;测点4位置的衬砌横向加速度响应频谱波形呈现三峰值现象,峰值频率分别为200、225和178.5 Hz,相对于测点2和测点3,存在一定程度的高频和中低频激励,测点4衬砌竖向加速度响应频谱波形呈现双峰现象,峰值频率分别为200 Hz和225 Hz,低频有一定激励但未有峰值出现,高频激励较弱;测点6位置衬砌横向加速度响应频谱波形呈现以172.5 Hz为峰值频率的单峰值现象,相对于测点2与测点3,测点6位置横向加速度响应低频激励较为明显但未出现峰值,而高频激励较弱;测点6位置衬砌竖向加速度响应频谱波形呈现以172.5 Hz和125 Hz为峰值频率的双峰值现象,相对于测点2与测点3,测点6位置竖向加速度响应低频激励较为明显且出现峰值,但高频激励较弱。对各测点横向加速度响应综合分析可知,各测点横向振动响应频率以中低频为优势响应频率,但随着高度的增加,低频及高频激励变化不明显;而对各测点竖向响应加速度综合分析可知,随着衬砌高度的增加,各测点竖向振动响应频率逐渐呈现多峰值状态,随着高度的增加,低频激励显著而高频激励降低。
通过计算可知,列车轮对系统固有频率的第二阶频率为173.2 Hz,与上述图中现场实测衬砌在列车荷载作用下横向和竖向加速度响应频谱峰值较为接近,由此可知衬砌在列车荷载作用下的加速度响应明显受到列车轮对第二阶固有频率的影响。
3 数值模型计算与验证
3.1 隧道数值模型建立
运用ABAQUS有限元软件,根据图1隧道尺寸和试验所选隧道现场的水文地质条件建立数值模型,对列车以300 km/h速度通过隧道时,衬砌拱圈加速度响应状态进行模拟。模型中隧道左侧土层与右侧土层厚度设为40 m,底层土体厚度设为40 m,上层覆土厚度选为30 m,采用CEP4进行单元网格划分,图21为隧道动力计算整体模型及网格划分。
3.2 模型材料物理力学参数
模型针对衬砌动力响应加速度进行分析,不考虑材料塑形应变,鉴于围岩材料本身具有复杂的物理力学特性,所以建立的隧道有限元计算模型中将围岩、二次衬砌均视为连续、各向同性的均匀介质,围岩采用摩尔库伦准则进行计算。按照文献[13]中相关规定,模型材料各主要参数如表1所示。

图21 整体模型及网格划分
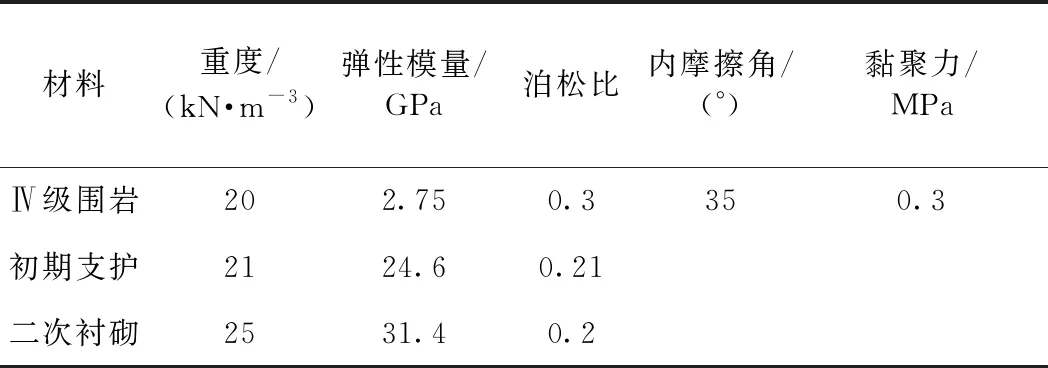
表1 模型材料主要参数
3.3 应力平衡与分析步设置
首先对隧道模型进行静力荷载工况计算,计算完成后提取各节点应力计算结果,将提取的节点应力与反力重新导入计算模型进行应力平衡,以消除静力荷载对衬砌造成的结构影响。

( 1 )
( 2 )
由隧道现场实测可知列车以300 km/h速度通过隧道断面所用时间约为2.5 s,以此为依据保守计算,模型中分析步时间设置为3 s,即动力隐式分析步总时长为3 s,积分步时长Δt=0.000 1 s。
3.4 荷载与边界条件
试验过程中,隧道现场实测点位于左线,所以模型中荷载加载方式设置为仅隧道左线行车,并将试验过程中运用力学轮轨力测试系统实测得到的速度300 km/h轮对轴间的列车荷载左垂力与右垂力(图22),分别施加于双线隧道下行线左轨接触路基与右轨接触路基。采用黏弹性边界条件[17]
( 3 )
( 4 )
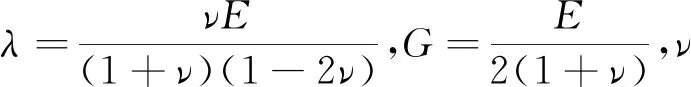
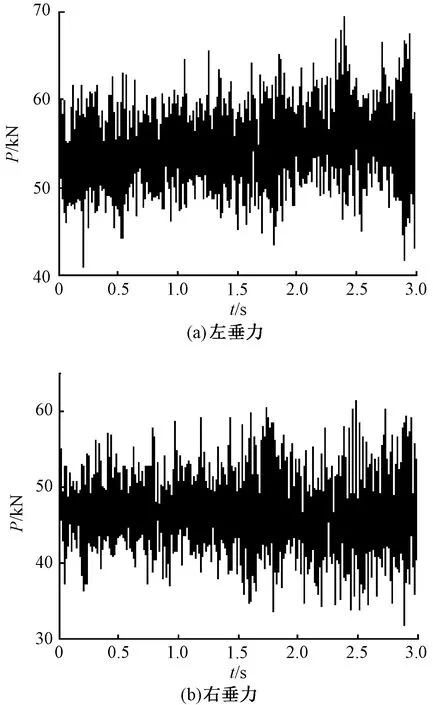
图22 速度300 km/h列车荷载实测值时程曲线

表2 观测点在拱圈坐标系对应角度值
3.5 数值计算结果与实测值对比分析
按照图23提取隧道模型数据,采用对称布置,每个节点间隔1 m左右,左右线各10个点,正拱顶提取1个点,共21个数据点,其中的左线节点1~6与隧道现场实测点位置相同。以过隧道圆心的水平线为x轴,拱顶与圆心连线为y轴建立笛卡尔坐标系,此时各数据节点位置用圆心角度表示,即节点19为0°,节点3为180°,各节点详细位置角度如表2所示。
因数值模拟与现场实测在数量级上保持一致,但实际数值存在一定的差异,此处为更直观方便地研究振动加速度在衬砌拱圈各位置的变化规律,对提取的模型计算数据进行归一化处理,将墙角节点1(200°)数值设置为单位1,其余节点数据根据与墙角节点1比例关系进行计算。以同样的方法,将现场隧道左线测点1实测值设为1,其余左右线测点数据依据比例关系进行归一化处理,并对应各测点角度关系,将模型计算数据与实测值数据归一化后统一绘制横向和竖向加速度趋势曲线,见图24和图25。
对数值模型计算结果和隧道现场振动实测值对比分析可得,模型计算结果与实测值结果具有相同数量级,且衬砌拱圈振动加速度响应传递规律基本一致,说明了模型在建立和计算过程中,计算方法、模型边界与约束条件、荷载施加方式和位置等参数的选取具有一定的适用性,能够满足实际衬砌拱圈加速度响应的计算需求,模型的建立和计算对今后研究不同时速列车荷载对衬砌振动加速度响应的影响规律具有一定意义。
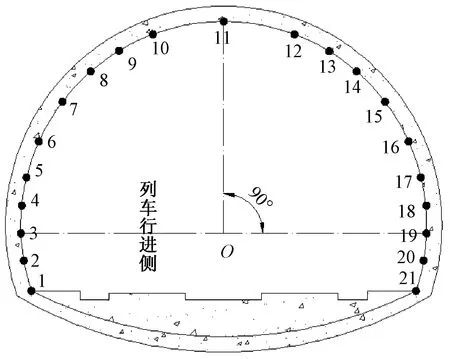
图23 模型数据提取点

图24 计算与实测横向归一加速度对比

图25 计算与实测竖向归一加速度对比
采用傅里叶级数对模型计算归一化结果数据进行归纳拟合,设单元节点竖向振动加速度归一化值为Av,At为单元节点竖向振动加速度归一化值,节点所在位置角度值为α(-20°<α<200°)。根据拟合计算数据可得数据前四阶函数拟合效果较好,而后随阶数的增加不再对数据相关性产生明显影响,所以此处采用四阶经验三角函数曲线公式拟合衬砌在300 km/h速度列车荷载作用下的拱圈振动响应规律
Av=αv1sin(βv1α+λv1)+αv2sin(βv2α+λv2)+
αv3sin(βv3α+λv3)+αv4sin(βv4α+λv4)
( 5 )
At=αt1sin(βt1α+λt1)+αt2sin(βt2α+λt2)+
αt3sin(βt3α+λt3)+αt4sin(βt4α+λt4)
( 6 )
式中:αv1=0.97,αv2=0.89,αv3=0.12,αv4=0.09;βv1=0.02,βv2=0.03,βv3=0.05,βv4=0.07;λv1=0.19,λv2=2.40,λv3=4.28,λv4=-1.25;αt1=0.69,αt2=0.72,αt3=19.17,αt4=18.62;βt1=0.46,
βt2=3.50,βt3=4.35,βt4=4.35;λt1=0.65,λt2=2.44,λt3=4.40,λt4=1.26。
将衬砌拱圈节点角度值代入式( 5 )、式( 6 )进行计算,并将计算结果与模型计算结果进行对比,其趋势曲线见图25、图26。由计算结果对比可知,拟合曲线误差小于5%,表明拟合曲线能够正确表示衬砌在列车荷载作用下的振动响应传递规律。因此,在今后的工作中,仅需知道衬砌拱圈任意位置的振动加速度响应和角度,代入公式进行计算,便可了解当前条件下的拱圈各位置衬砌加速度响应数据。
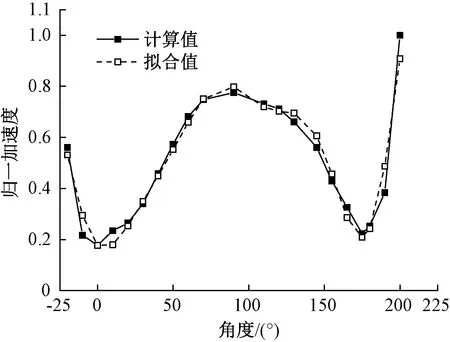
图26 横向加速度拟合数据与计算值曲线
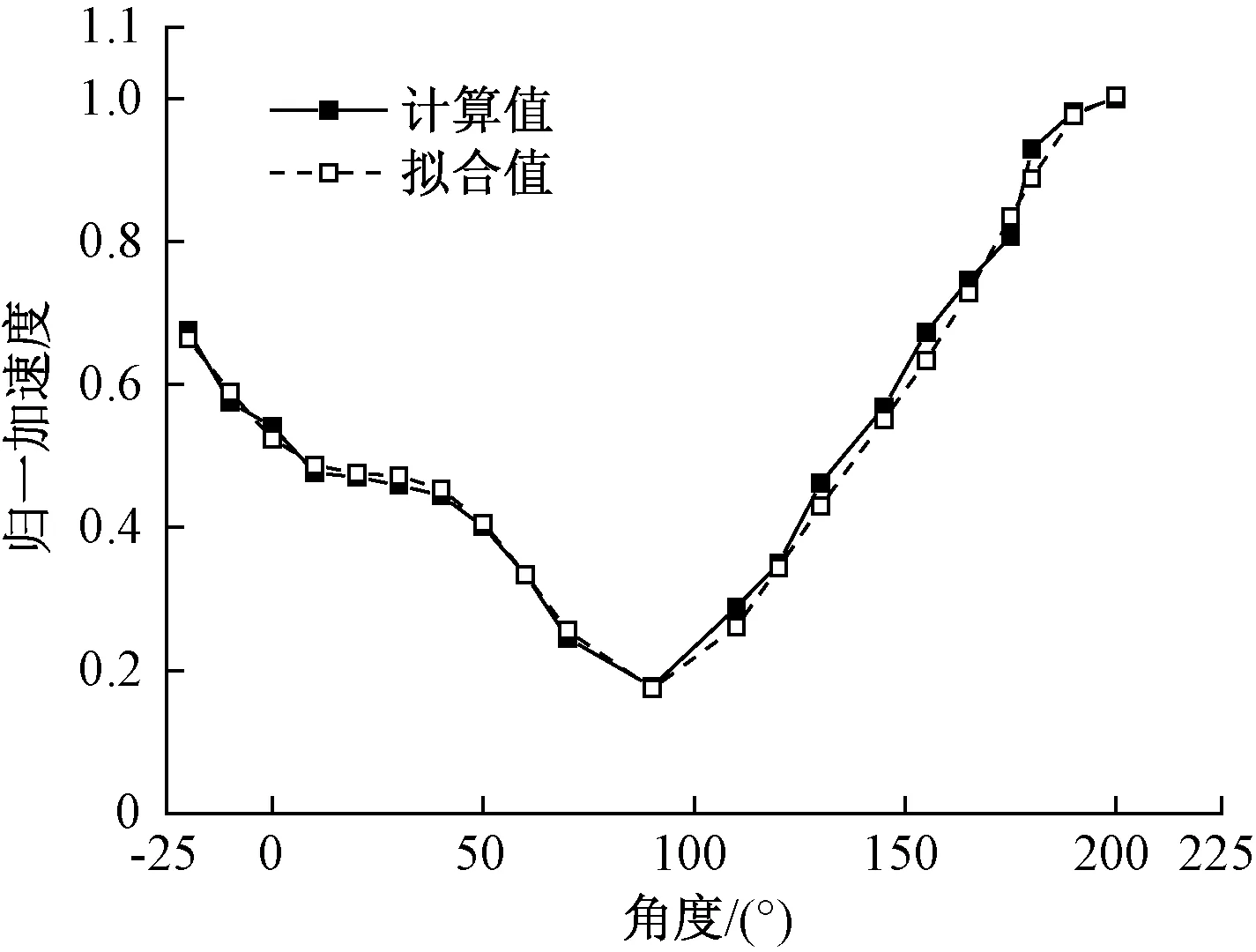
图27 竖向加速度拟合数据与计算值曲线
4 结论
通过对隧道衬砌在速度300 km/h列车荷载作用下的现场实测与模型计算研究,得到以下结论:
(1)隧道衬砌在列车荷载作用下的竖向振动加速度响应在墙角处最大,拱顶处最小,由墙角向拱顶随高度的增加呈下降趋势,衬砌与列车距离对衬砌加速度响应值具有较大影响,列车距衬砌越近其振动响应值越大。
(2)衬砌拱圈在列车荷载作用下的横向振动响应加速度,在隧道墙角高度为0位置出现最大值,而后在高度1 m处突降至最低,后又随隧道衬砌拱圈高度的增加逐渐增大,列车远近仅影响衬砌横向加速度响应相对值大小,且衬砌横向加速度响应不具备较高的离散性。
(3)动车组列车轮对二阶固有频率对隧道衬砌拱圈振动加速度响应频率具有较大影响,且低频激励随着拱圈高度增加而逐渐显著。
(4)文中数值模型的计算方法、模型边界条件、约束和荷载施加方式等参数的选取具有一定的适用性,能够满足实际衬砌拱圈加速度响应的计算需求,对日后研究不同时速列车荷载对衬砌振动加速度响应的影响规律具有一定的参考意义。
(5)依据模型数据与实测数据拟合了振动沿衬砌拱圈传递的三角函数关系,函数计算结果适应性良好,对后续研究列车荷载作用下的拱圈振动加速度响应机制提供了一定参考。
