新型装配式拱圈节段的转动刚度分析与设计研究

刘长海

（中铁建大桥工程局集团第三工程有限公司 辽宁沈阳 110043）

1 引言

混凝土拱桥历史悠久，在山区地形、地质较好的条件下，拱桥桥型具有很强的竞争力。在德国高速铁路VDE8线路上，29座穿越森林的跨谷桥梁中，就有10座采用了混凝土拱桥［1］。

根据国内外多年积累的经验，目前的拱桥施工方法主要包括转体施工法［2］、拱架施工法［3］、悬臂施工法［4］、缆索吊装施工法和劲性骨架施工法［5］等。因为具有经济效益高，施工安全方便、适应性较广和跨越能力较大等优点［6－9］，缆索吊装施工现已成为大跨度拱桥的主要施工方法且发展迅速。1968 年，郑皆连［10］8提出钢丝绳斜拉扣挂系统，使用悬拼双曲拱圈的方法使拱桥的施工可以不再搭设拱架，极大简便了跨径100 m左右的混凝土拱桥的施工，使跨径突破了 150 m；1994 年，郑皆连［10］8又提出千斤顶和钢绞线斜拉扣挂系统，再一次使拱桥悬拼的经济性、安全性和精度大大提高；2002年，云南小湾大桥［11］成功将预应力锚索用于大型起重设施的锚碇；2006年，重庆菜园坝长江大桥［12］完成合龙，缆索吊中跨长420 m，吊重可达4 200 kN，为当时世界之最；2012年，李开心等［13］根据缆索吊装施工中存在的不足，在考虑温度对施工影响的基础上，提出无应力状态控制法，并得到了缆索吊装系统中无应力长度计算公式；2019年，牛路河特大桥采用缆索吊装技术施工，拱圈节段间首次采用企口加胶接与临时精轧螺纹钢组合的新型连接形式，不但实现了节点之间快速精准匹配，确保拼接精度，而且解决了因装配式混凝土节段自重较大，加上主拱圈设有弧度而导致临时锚固装置失效的问题。

由于牛路河特大桥拱圈节段间的连接刚度与拱圈其他部位存在显著差异，特别是在胶拼处，而且作为一种新型连接形式，目前还没有计算方法确定其节段间平面内转动刚度。本文为适应工程人员需求，假设混凝土为刚体，最终得到节段间转动刚度的简便计算方法；进而使用ABAQUS建立精细化有限元模型以验证简便计算方法的准确性与可行性；最后考虑节段间刚度取计算值或刚接，分别建立拱圈Midas施工阶段模型，根据位移与应力计算结果的对比说明采用该新型连接形式的优势。

2 工程背景

2.1 桥梁概况

牛路河特大桥系张花高速公路工程上的一座特大桥。桥梁全长430.08 m，桥面宽10 m，主桥为桥跨布置形式5×20 m＋195 m＋5×20 m的上承式混凝土拱桥，拱肋计算跨径为195 m，拱轴线为悬链线，矢高及矢跨比分别为39 m和1/5，拱轴系数m为1.543，见图1。主拱圈截面形式为单箱两室断面，高360 cm（等高），宽780 cm，详细尺寸见图2。扣、锚索材料采用1 860钢绞线，拱圈采用C50混凝土，扣塔塔墩采用C50混凝土，竖杆采用Q345钢材，连接系采用Q235钢材。

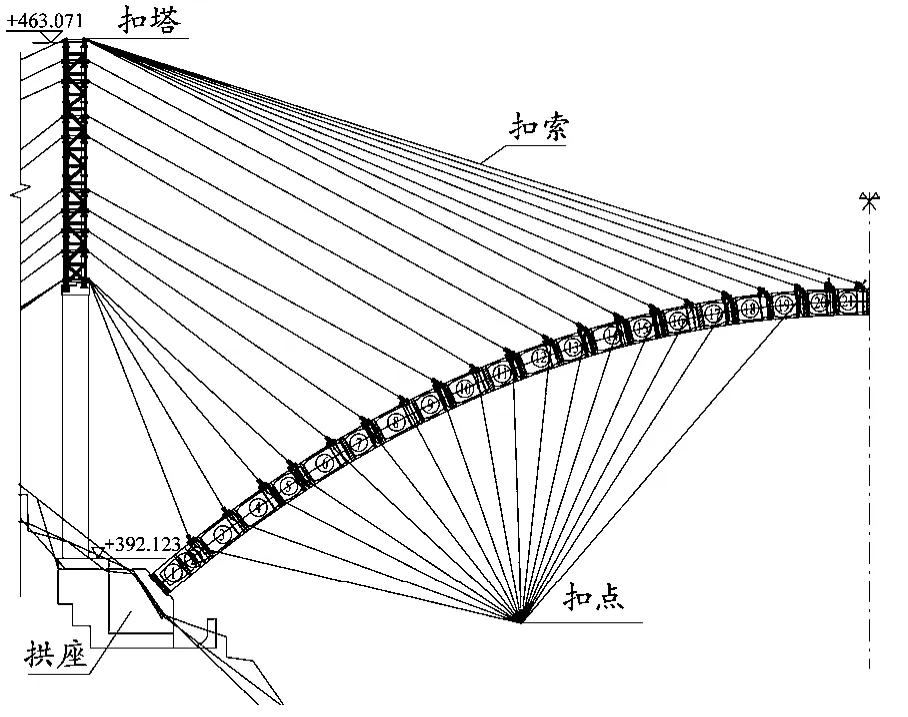
图1 拱圈施工节段（单位：m）

图2 拱圈箱室标准段截面尺寸（单位：cm）

2.2 施工方法

预制吊装的拱箱沿拱轴线全长共分为42个节段，由于是根据拱上立柱及吊装重量控制进行的拱肋节段划分，所以每个节段长度均不同。拱肋采用梁场预制、吊装，还设有7个现浇段，现浇段的拱轴线长为0.6 m，另外还布设了2个拱脚现浇段，长度均为0.76 m。预制拱脚节段与拱座先铰接，待拱圈调好角度后，再采用超垫法进行支撑，不仅可以调整拱圈线形，而且节点之间连接牢固，解决了受悬臂扰动敏感性强、拱圈根部易开裂的问题。拱圈每个施工节段间的连接主要有企口＋胶接和混凝土湿接缝两种方式，另外还施加了精轧螺纹钢的临时预应力连接，见图3。

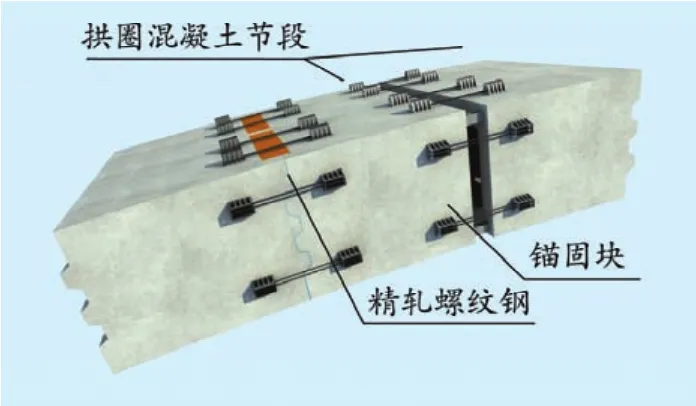
图3 拱圈节段间胶拼与湿接缝连接

拱圈应用缆索吊装法施工，在预制场内完成预制后（埋设相关的预埋件），由运输车运送至起吊区，然后再横向移动至主索下方，最后再由缆索吊机起吊安装。安装顺序为由两岸向跨中逐节段安装、扣挂，直至最终合龙。扣挂系统主要由锚碇、扣塔和扣锚索等组成，分别在两岸布设扣塔，塔高33.14 m；除了1＃节段外，每个拱圈节段都设置1层扣锚索，全桥共设40层扣锚索，两侧各20层，每层扣锚索横桥向布置2束，扣锚索编号与拱箱节段编号对应。拱圈施工节段图见图1，主要施工步骤见表1。

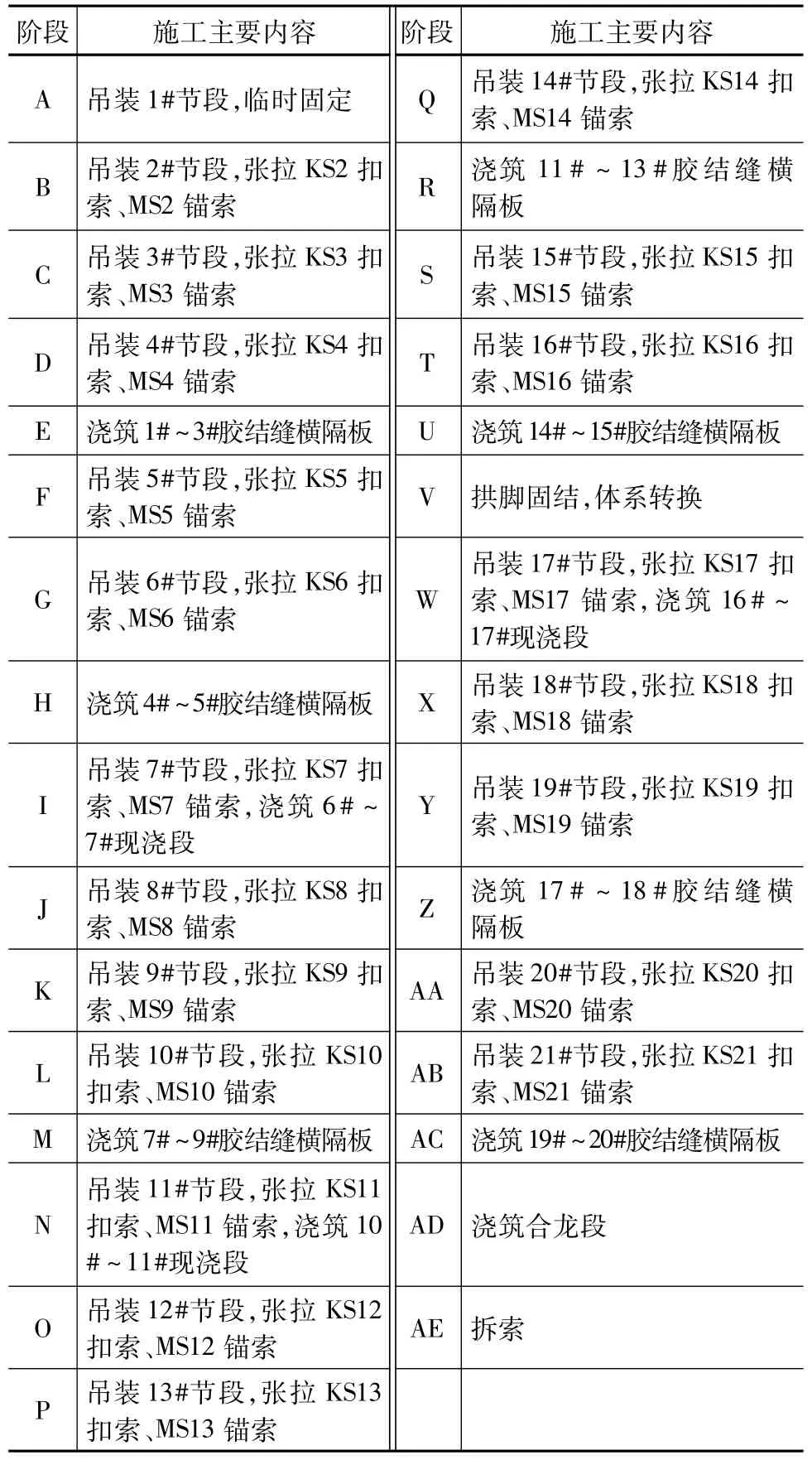
表1 拱圈主要施工步骤

3 拱圈节段间平面内转动刚度计算方法研究

根据图3，由于拱圈节段间的连接刚度与拱圈其他部位存在显著差异，特别是在胶拼处。而在Midas建立拱圈施工模型过程中，默认每个施工节段间为刚接，因此需计算出拱圈节段间平面内转动刚度，而后用释放梁端约束的方式将该转动刚度施加到Midas模型的相应位置。

3.1 混凝土刚体化后的简化计算方法

为得到拱圈节段间平面内转动刚度的简化计算方法，假设如下：

（1）在拱圈施工过程中，每一个施工节段之间仅接触而不连接；

（2）混凝土视为刚体，即每个施工节段吊装完成后，将绕接触面的最下缘（见图4）转动，仅考虑临时预应力精轧螺纹钢提供的转动刚度km，计算方法见式（1）。

式中，θ为假设的转角（rad）；l为钢筋对转动轴（见图4）的力臂长度（m）；Fs为钢筋的内力（kN）。

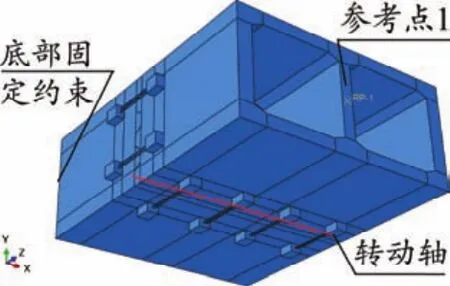
图4 拱圈节段ABAQUS模型的整体效果

首先假定节段间绕转动轴产生一个很小的转角，然后根据钢筋到转动轴的力臂长度l和钢筋长度ls便可计算出钢筋应变（εs＝θl/ls），进而得到钢筋应力和内力。根据以上两条假设、计算方法和临时预应力精轧螺纹钢的布置位置及尺寸，每个施工节段间平面内转动刚度计算过程及结果见表2。

表2 拱圈节段间的转动刚度计算过程及结果

续表2

3.2 精细化有限元模拟分析

由于在简化计算拱圈节段间平面内转动刚度时过于理想化，特别是假设2将混凝土视为刚体，因此需要验证其正确性，此处建立拱圈节段ABAQUS精细化有限元模型，计算其转动刚度，模型的整体效果图见图4。

其具体建模过程如下：

（1）部件和特性：建立拱圈混凝土节段、钢筋和锚固块部件，然后设置材料和截面特性并将其赋予给相应的部件，其中，锚固块为Q345钢材，精轧螺纹钢的直径为40 mm。

（2）装配与分析步：通过装配模块将部件实体最终装配成图4所示的模型；除了软件本身带有的initial分析步以外，还建立了4个静力分析步。

（3）相互作用：每个分析步中，两个拱圈混凝土节段间都建立面－面硬接触，不考虑混凝土接触面之间的摩擦效应和胶的作用；将拱圈混凝土节段与锚固块、钢筋和锚固块间接触的面定义成绑定约束；在图4所示面上建立参考点1，并将参考点与其所在面建立耦合作用。

（4）荷载与边界条件：第一个分析步给每根钢筋施加了10 kN的预应力，目的是为了测试模型的正确性；第二个分析步施加了440 kN的预应力，目的是使精轧螺纹钢的预紧力达到施工时的预紧力，即450 kN；第三个分析步只将钢筋保持为当前长度，让钢筋保持为上一分析步结束时的长度，目的是为了测试在没有其他外荷载下，钢筋受力和长度是否会变化；最后一个分析步中仍然将钢筋保持为当前长度，另外还在参考点1的位置施加了沿y轴负方向（见图4）8 000 kN的力；底部添加固定约束。

（5）划分网格：网格划分效果见图5。

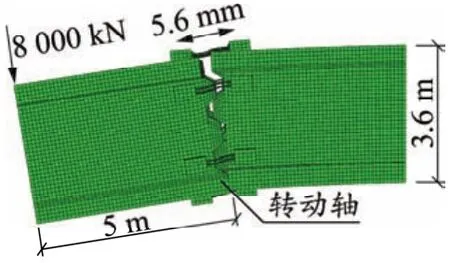
图5 第四个分析步结束时的变形

根据计算结果，第三个分析步结束时，钢筋的压缩量为0.4 mm，混凝土的压缩量基本为0；第四个分析步结束时，变形见图5，顶板混凝土张开后的水平方向间距为5.6 mm，底板混凝土的水平方向间距基本为0。根据变形结果，得两拱圈节段间对于转动轴的转角θ为顶板混凝土张开的水平距离与拱圈阶段高度的比值，即：

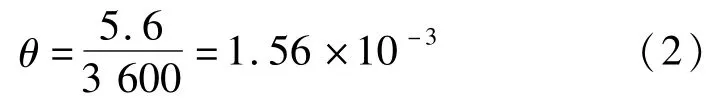
由图5，外力对转动轴的力矩为参考点1处的外力乘以拱圈阶段长度，即8 000 kN×5 m，最终得到节段间的转动刚度为外力对转动轴的力矩与转角θ的比值：

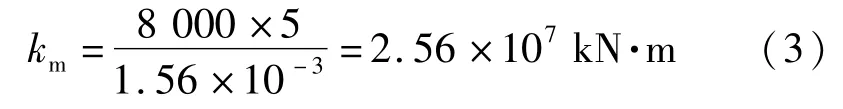
这与3.1节简化计算结果十分接近，仅相差15%左右，说明混凝土对拱圈节段间的转动刚度影响不大，主要还是精轧螺纹钢起作用，将混凝土刚体化后的简化计算方法有效。

4 拱圈节段间平面内转动刚度折减的必要性

4.1 拱圈施工阶段Midas模型建立

为更加精确地模拟拱桥施工状态，塔架与拱圈建模采用梁单元，锚索、扣索建模则采用桁架单元。按表1中的施工步骤设置相应的模型施工阶段，每一拱圈节段划分为一个施工阶段，则从1＃～21＃共有21个节段，另外浇筑合龙段及拆索分别划为一个施工阶段，因此共计23个施工阶段。锚索与塔架均采用固定约束，拱脚位置先采用临时固接，浇筑14＃～15＃胶结缝横隔板后使拱脚固接，见表1，计算模型见图6。

图6 拱圈Midas施工阶段模型

4.2 位移和应力计算结果

在拱圈Midas施工阶段模型中，扣索的索力是相同的，仅有节段间转动刚度这一个变量不同，每个拱圈节段间的平面内转动刚度依次用刚接、3.1节简化计算结果和3.2节精细化建模得到的结果进行模拟，然后通过对比三次模型中拱圈和塔架各部分最大应力与位移计算结果的差异，同时与施工监控数据进行对比，验证对拱圈节段间平面内转动刚度折减的可行性、必要性和节段间新型连接形式的优势，计算结果见表3。

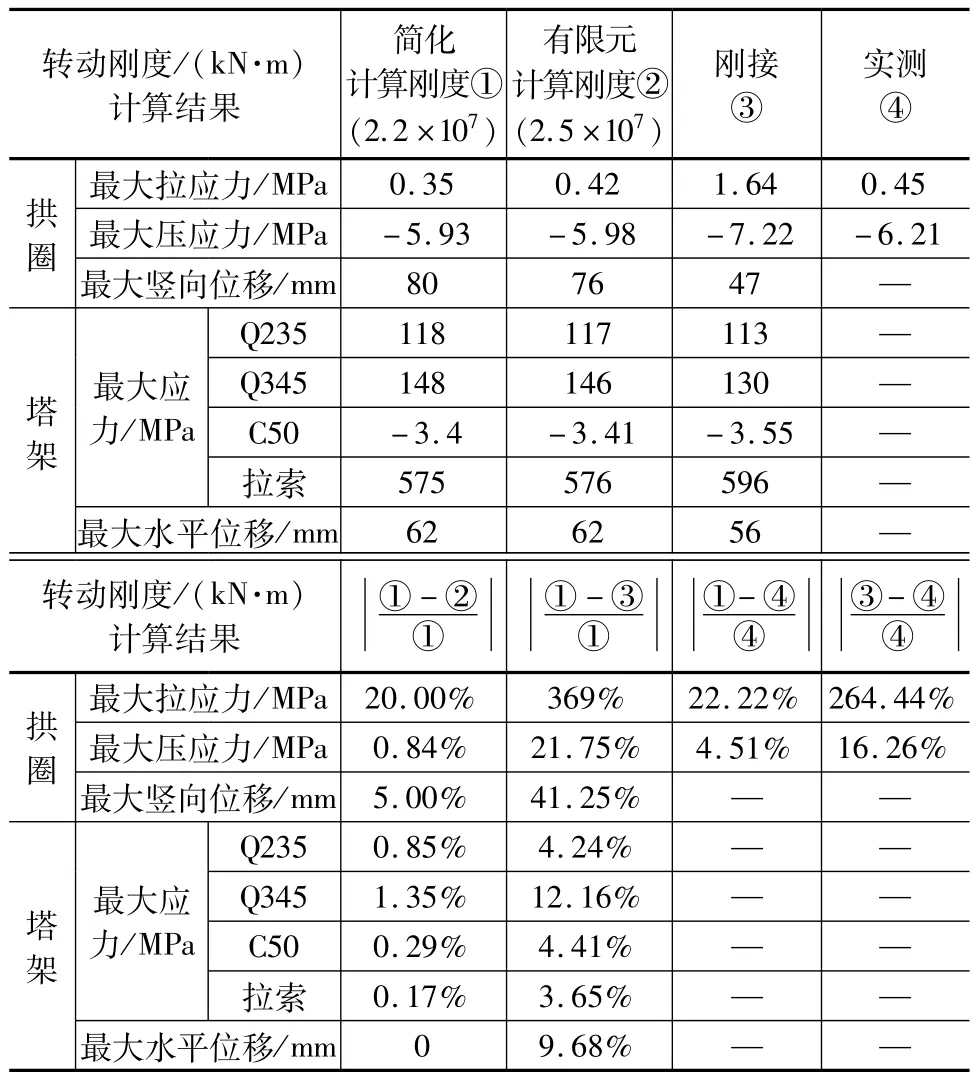
表3 节段间不同转动刚度下拱圈施工阶段计算结果

根据表3可知相对于刚接，利用刚度折减得到的拱圈施工阶段最大应力模拟结果与实际监控数据更接近，进一步验证了混凝土刚体化后的拱圈节段间平面内转动刚度简化计算方法的正确性；随着拱圈节段间平面内转动刚度的增加，拱圈混凝土最大压应力和最大拉应力递增，最大竖向位移递减，原因为对于超静定体系，构件刚度大，分配所得的内力多，应力递增；拱圈节段间平面内转动刚度变化对拱圈最大拉应力的影响最显著，刚接时约为折减后的4倍，而后依次为拱圈位移和压应力，对塔架的应力和位移影响最小，误差均在15%以内。

5 结论

本文以牛路河特大桥为背景，探究新型装配式混凝土拱桥拱圈节段间平面内转动刚度的计算方法，并通过精细化有限元模拟进行验证，同时考虑不同拱圈节段间平面内转动刚度，建立拱圈Midas施工阶段模型，验证对转动刚度折减的必要性和可行性，最终得到如下结论：

（1）混凝土刚体化后简化计算的拱圈节段间平面内转动刚度和ABAQUS精细化有限元模拟的结果十分接近，两者相差仅15%；同时相对于刚接，利用此刚度得到的拱圈施工阶段最大应力模拟结果与实际监控数据更吻合，说明混凝土对拱圈节段间的转动刚度影响不大，主要是临时精轧螺纹钢起作用，将混凝土刚体化后的简化计算方法可行且正确。

（2）相对于拱圈节段间刚接，新型连接形式不仅使拱圈在施工过程中的最大拉应力显著减小，有效降低拱圈混凝土开裂风险，而且能确保拼接精度，成功保障了拱圈能安全有效快速施工。

（3）拱圈节段间采用企口＋胶接与临时精轧螺纹钢组合的新型连接形式可以有效降低拱圈节段间平面内转动刚度，使拱圈在施工阶段的最大拉应力和最大压应力都减小，因此该新型连接形式具有很好的发展前景。