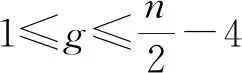BC网络的g-超条件诊断度
2020-07-13刘爱霞王世英
刘爱霞,王世英
(1.山西大学 数学科学学院,山西 太原 030006;2.太原科技大学 应用科学学院,山西 太原 030024)
0 引言
随着半导体技术的飞速发展,大规模并行系统互连网络的规模迅速扩大,例如天河2号系统包含3 120 000个结点,Cray Titan包含560 640个结点[1]。大规模并行计算机系统在使用过程中总是需要不间断地运行。因此,系统互连网络具有高的容错性和可靠性非常重要。而且,当系统中处理器发生故障时,为了保持系统可靠性,系统中故障处理器需要及时被诊断出来并替换。识别故障结点的过程称为系统的故障诊断。1967年,Preparata[2]首次将图论方法应用于系统的故障诊断,创建了第一个系统级故障诊断模型,称为PMC模型。之后,人们提出了许多系统级故障诊断模型,例如Chwa 和 Hakimi模型[3]、比较模型(也称MM模型)[4]、 BGM模型[5]等。PMC模型和MM模型是系统级诊断最常采用的两个模型。
如果一个系统被称为是t-可诊断的,则系统中故障结点不超过t个且不经过替换可以一次性识别出来。使得系统G是t-可诊断的最大整数t称为系统G的诊断度,记作t(G).作为度量大规模并行处理器系统的故障诊断能力的经典参数,诊断度总是假设系统的任一处理器的集合都可以同时发生故障。特别地,假设某个顶点v的所有邻点同时发生故障,则此时我们将无法判断顶点v是否故障。故系统的诊断度总是小于其最小度。然而,在大规模并行系统中上述情形出现的概率几乎为0。因此,诊断度低估了系统互连网络的故障诊断能力。为了更精确地度量互连网络的系统级故障诊断能力,人们对系统中处理器的故障情形加以限制,提出了多种新的条件诊断度,具体参见文献[6-10]。
受到g-超连通度概念的启发,Zhang等[11]假设系统中非故障结点构成的分支的顶点数至少为g+1, 提出了g-超条件诊断度的概念。同时,Zhang等[11]还研究了PMC和MM*模型下超立方体的g-超条件诊断度,得到了如下结果。
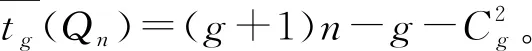
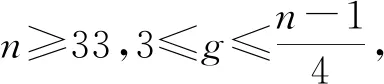
Bijective connection网络(简称BC网络)是一类基于立方体的网络,它包含许多著名的互连网络,譬如超立方体、莫比乌斯立方体、交叉立方体、纽立方体等。莫比乌斯立方体、交叉立方体、纽立方体都是超立方体的变形网络,它们具有更好的性质,例如它们的直径是相同维数下的超立方体的二分之一。对BC网络的性质进行研究,可以同时获得超立方体、莫比乌斯立方体、交叉立方体、纽立方体等网络的相关结果。因此,BC网络的研究得到了广泛的关注。本文研究了PMC和MM*模型下BC网络的g-超条件诊断度。
1 术语和记号

cn(G)=max{|NG(u)∩NG(v)|:u,v∈V(G)}。
设S为顶点集V(G)的子集若S中任意两点在G中均不相邻,则称S为G中独立集。图G中最大独立集的阶数称为G的独立数,记作α(G)。若图G去掉顶点集F后不连通,则称F是图G的一个割。若图G存在割,则最小割的顶点数称为图G的连通度,记作κ(G)。否则,规定图G的连通度κ(G)为(|V(G)|-1)。图G中最短圈的长称为G的围长,记作g(G),未定义的术语和记号参见文[12]。
一个n维BC网络Bn是一个阶为2n的n-正则图。Bn能被递归地定义如下[13]。
定义1[13]1维BC网络B1是一个2阶完全图。1维BC网络类B1={B1}。一个图G被称为一个n维BC网络,其中n≥2, 若它满足如下条件:
(1)V(G)=V0∪V1,V0∩V1=Φ且导出子图G[V0],G[V1]是(n-1)维BC网络;
(2)顶点集V0和V1之间的边恰为图G的一个完美对集。
所有n维BC网络的集合,称为n维BC网络类,记作Βn。
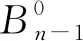

图1 两个BC网络
容易看到,n-维BC网络Bn是n-正则的,且当n≥2时,它的围长是4。
下面,给出系统诊断的一些概念和结果。
并行计算机系统互连网络的系统级故障诊断问题的研究依赖于测试模型的建立。不同的测试模型反映了实际系统中所采用的不同的测试方法以及对测试结果的不同解释。在PMC模型下,相邻的两个处理器之间可以相互进行测试[2]。对于系统G(V(G),E(G))中的两个相邻顶点u和v有序顶点对(u,v)代表从u到v的测试,u称为测试者,v称为被测试者。我们用σ(u,v)表示测试结果其中σ(u,v)取1和0,它表示被测试者是否发生故障。当u是故障的,测试结果是不可靠的,即无论v是否发生故障,σ(u,v)可能取0,也可能取1。但当u是非故障时,若v是非故障的,则σ(u,v)为0;若v是故障的,则σ(u,v)为1。
对系统G的一次测试是指对G中每对相邻点都进行一次相互测试,它可以用一个有向图T(V(G),L)表示,其中uv∈L表示u和v在图G中相邻。对系统G的一次测试T的所有测试结果的集合称为系统G的一个症状,记作σ。换句话说,系统G的一个症状σ是一个函数σ∶L→(0,1).G中所有故障点的集合称为它的故障集。显然,它是G的顶点子集。
对于给定的症状σ, 若存在顶点子集F⊆V, 对于任意一条边uv∈L,都有u∈VF,σ(u,v)=1当且仅当v∈F,则称故障集F与症状σ是一致的。对不同的顶点子集F1和F2,若σ(F1)∩σ(F2)≠Φ,则称F1和F2是不可区分的,F1和F2为不可区分的点集对;否则,称F1和F2是可区分的,F1和F2为可区分的点集对。
在MM模型下,一个(测试)处理器同时对它的两个相邻(被测试)处理器发送相同的测试任务,然后比较它们反馈的测试结果,通过这样的方式来实现对故障处理器的识别[4]。在MM模型下,通常有以下几个假设:
(1)所有的处理器故障都是永久的;
(2)有故障的被测试处理器对测试任务的输出结果总是错误的;
(3)由发生故障的测试处理器产生的比较结果是不可靠的;
(4)给两个被测试故障处理器发送相同的测试任务或输入总产生不一样的输出结果。
系统G的一个比较策略可以通过一个多重图M(V(G),L)来模拟,其中L表示被标记的边的集合。 一条标记边(uv)w∈L表示一个由顶点w对顶点对{u,v}进行比较测试,这意味着在G中uw,vw∈E(G)。在M(V(G),L)中,所有比较的结果组成的集合称为诊断的一个症状,记作σ*。在σ*中,σ*(u,v)w表示顶点w对被测试点对{u,v}的输出结果的比较结果。如果比较(uv)w的结果不一致,则σ*(u,v)w=1;否则,σ*(u,v)w=0,因此,一个症状σ*是一个函数:σ*∶L→(0,1)。MM*模型是MM模型的一种特殊情况。在MM*模型下,G中所有可能的比较都必须被实施即 若uw,vw∈E(G), 则 (uv)w∈L。
在MM模型下,若症状σ*和顶点集F满足下列条件:
(1)若u,v∈F且w∈V(G)F,则σ*(u,v)w=1;
(2)若u∈F且v,w∈V(G)F,则σ*(u,v)w=1;
(3)若u,v,w∈V(G)F则σ*(u,v)w=0,
则称σ*是可由F产生的。若σ*可由F产生,则称F与σ*是一致的。
由于发生故障的测试处理器产生不可靠的结果, 故一个故障集可能产生不同的症状。 令σ*(F)是与F一致的症状的集合。对不同的顶点集F1,F2⊂V(G), 若σ*(F1)∩σ*(F2)=ø,则称F1和F2是可区分的,F1和F2为可区分的点集对; 否则称F1和F2是不可区分的,F1和F2为不可区分的点集对。
定义2[2]设G是一个互连网络。在不被替换的情况下,如果G中故障结点的个数不超过t时,所有故障都能被一次性诊断出来,则称网络G是t-可诊断的。系统G的诊断度是使得G是t-可诊断的t的最大值,记作t(G)。
在文[6]中,Lai等给出了网络G是t-可诊断的一个等价定义。
定义3[6]网络G是t-可诊断的当且仅当G中任意两个满足|F1|≤t,|F2|≤t的顶点集F1,F2都是可区分的。
为了更精确地度量互连网络的故障诊断能力,Lai等[6]提出了条件诊断度的概念。
定义4[6]设F是网络G=(V,E)的一个顶点子集。若G中任意一个顶点v的邻集均不包含于F则称F为G的一个条件集。若G中任意两个满足|F1|≤t,|F2|≤t的条件集F1,F2都是可区分的,则网络G是条件t-可诊断的。网络G的条件诊断度是使得G是条件t-可诊断的t的最大值,记作tc(G).
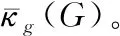
受条件诊断度和g-超连通度概念的启发,Zhang等[11]对分支的结点数加以限制,提出了g超条件诊断度的概念。

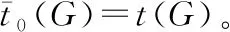
引理1[16]设F1,F2是图G的两个相异的顶点子集。顶点集F1和F2在PMC模型下是可区分的当且仅当存在顶点u∈V(F1∪F2),v∈F1ΔF2使得uv∈E(G), 如图2。

图2 PMC模型下的可区分点对(F1,F2)
Sengupta和Dahbura[17]给出了MM*模型下顶点集F1和F2可区分的一个充要条件。
引理2[17]设F1,F2是图G的两个相异的顶点子集。顶点集F1和F2在MM*模型下是可区分的当且仅当下列情形之一成立(如图3):
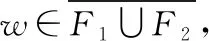
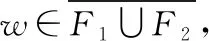

图3 MM*模型下的可区分点对(F1,F2)
2 BC网络在PMC和MM*模型下的g-超条件诊断度的下界
本节,我们将在BC网络的容错性的已有结果的基础上,进一步讨论BC网络在PMC和MM*模型下的g-超条件诊断度的下界。 首先,介绍Fan等[13]得到的BC网络Bn的(g+1)阶子图的邻集的性质。
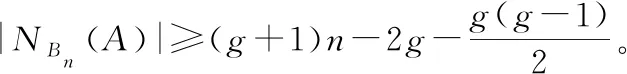
2012年,Yang等[18]研究了Bn的g-超连通度,给出了它的一个下界。

下面的函数在Bn的g-超条件诊断度的研究中具有重要的作用。通过简单的计算,容易得到下面的引理。
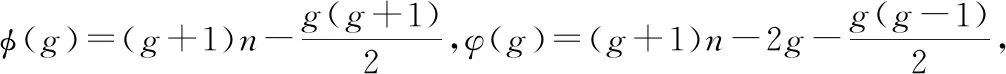
(1)当1≤g≤n-1时,函数φ(g)严格单调递增;
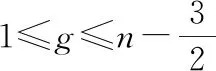
下面,我们给出一个简单的引理。
引理6 当n≥1时,BC网络Bn的独立数α(Bn)≤2n-1。

下面,我们讨论PMC模型下Bn的g-超条件诊断度的下界。


|V(Bn)|-|F1∪F2|≥
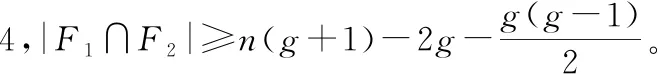
注意到F2F1≠ø且Bn[F2F1]的每个分支包含至少(g+1)个顶点,故|F2F1|≥g+1,因此
|F2|=|F1∩F2|+|F2F1|≥
与F2的取法矛盾。证毕。
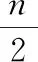

|V(Bn)|-|F1∪F2|≥



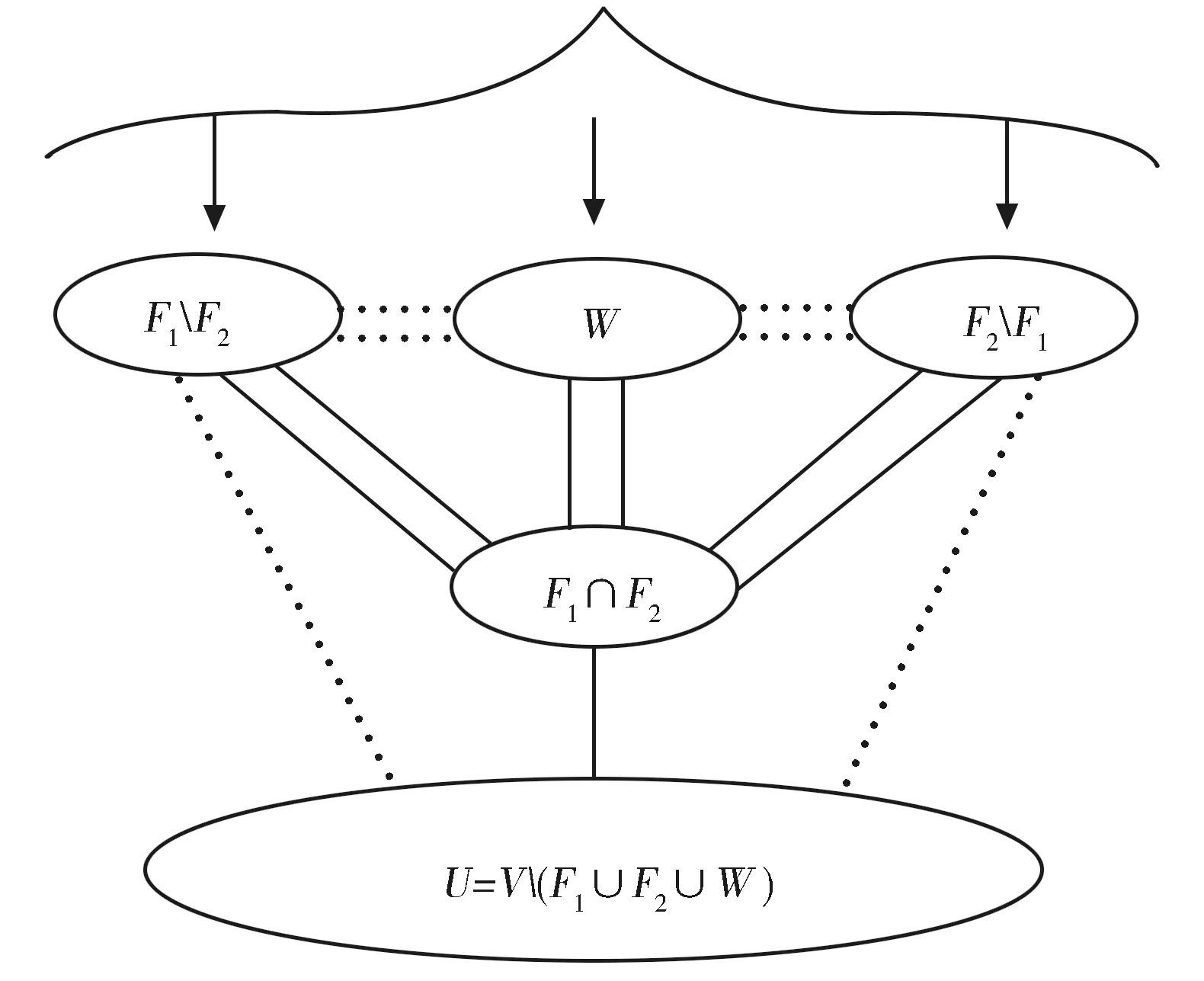
图4 断言1中V(G)的分解
由引理6,|W|≤2n-1,从而,对任意的w∈W,NBn(w)⊆F1∪F2。下证F1F2≠ø,否则,NBn(w)⊆F2。由此可知w是Bn-F2中的孤立点。故g=0, 与题设g≥1矛盾。类似地,F2F1≠ø。因此,
|F1∩F2|=|F1|-|F1F2|≤
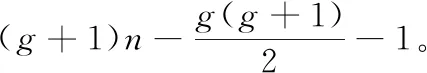
(1)
设w为W中一点。假设|NBn(w)∩(F1F2)|≥2,则存在u,v∈F1F2使得uw,vw∈E(Bn).由引理 2(2),(F1,F2)是可区分的,与(F1,F2)不可区分矛盾。故|NBn(w)∩ (F1F2)|≤1。若|NBn(w)∩(F1F2)|=0,则NBn(w)⊆F2,从而推出w是Bn-F2中的孤立点,即g=0,与题设g≥1矛盾。故
|NBn(w)∩(F1F2)|=1。
同理可得
|NBn(w)∩(F2F1)|=1。
因此,
|NBn(w)∩(F1∩F2)|=
|NBn(w)|-|NBn(w)∩(F1F2)|-
|NBn(w)∩(F2F1)|=
|NBn(w)|-2=n-2。
由此可得,
|F1∩F2|≥|NBn(w)∩(F1∩F2)|=n-2。
设U=V(Bn)(F1∪F∪W).下证U≠ø.反之假设U=ø,则
2n=|V(Bn)|=|F1|+|F2|-
|F1∩F2|+|W|≤


由引理4,

|F1F2|≤g且 |F2F1|≤g。

|F1∩F2|≥|NF1∩F2(W)|≥
|NF1∩F2(W′)|≥
|NBn(W′)|-|F1F2|-|F2F1|≥
再由(1)可以推出
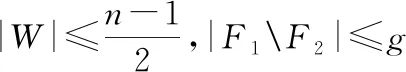
|V′|-1=|F1F2|+|F2F1|+
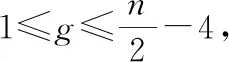
另一方面,因为F1和F2都是Bn中的g-超割且U和V′之间无边,所以|W|+|F1F2|≥g+1,|W|+|F2F1|≥g+1。再由F1F2≠ø和F2F1≠ø,我们有
|V′|-1=|F1F2|+|F2F1|+
|W|-1≥g+1。
显然,NBn(V′)⊆F1∩F2。故|NBn(V′)|≤|F1∩F2| .由引理3和引理5(2),
|F1∩F2|≥|NBn(V′)|≥
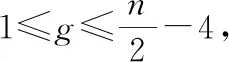
也就是
然而,由题设可知,
矛盾。断言证毕。
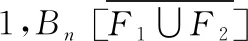
另一方面,因为F1∩F2是Bn的g超割,所以|F1F2|≥g+1,从而,
|F1|=|F1∩F2|+|F1F2|≥
与F1的取法矛盾。证毕。

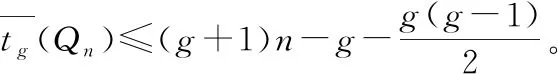
结合定理3、定理4和引理7可得PMC和MM*模型下超立方体Qn的g-超条件诊断度。
推论1设n,g是两个整数,则

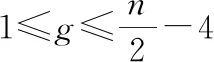
显然,推论1(1)是定理1, 推论1(2)改进了定理 2。 另外,推论1表明定理3和定理4给出BC网络的g-超条件诊断度的下界是紧的。
3 g较小时,BC网络在PMC和MM*模型下的g-超条件诊断度
本节进一步讨论了当1≤g≤3时,BC网络在PMC和MM*模型下的g-超条件诊断度。应用所得结果,许多著名的互连网络的g(1≤g≤3)超条件诊断度被给出,譬如交叉立方体、莫比乌斯立方体和纽立方体等。为了得到本节的主要结果,我们首先介绍BC网络一些重要的性质。
引理8[19]设Bn∈Βn,则
(1)|V(Bn)|=2n;
(2)Bn是n-正则的;
(3)当n≥2时,cn(Bn)=2且Bn的围长为4;

为了叙述方便,我们用Pt表示阶为t的路,用Kt表示t个顶点的完全图。
引理9[20]设Bn∈Βn,则
(1)设K1和P3为Bn中两个顶点不相交的子图且n≥2,则cnBn(K1,P3)≤4;
(2)设K2和P3为Bn中两个顶点不相交的子图且n≥3,则cnBn(K2,P3)≤7;
(3)设K1和K1,3为Bn中两个顶点不相交的子图且n≥3,则cnBn(K1,K1,3)≤5;
(4)设K1和P4为Bn中两个顶点不相交的子图且n≥3,则cnBn(K1,P4)≤5;
(5)设K2和K1,3为Bn中两个顶点不相交的子图且n≥3,则cnBn(K2,K1,3)≤9;
(6)设K2和P4为Bn中两个顶点不相交的子图且n≥3,则cnBn(K2,P4)≤9;
(7)设P3和K1,3为B6中两个顶点不相交的子图,则cnB6(P3,K1,3)≤12;
(8)设P3和P4为B6中两个顶点不相交的子图,则cnB6(P3,P4)≤12;
(9)设P3和K1,3为Bn中两个顶点不相交的子图且n≥3,则cnBn(P3,K1,3)≤13;
(10)设P3和P4为Bn中两个顶点不相交的子图且n≥3,则cnBn(P3,P4)≤13。
假设H∈Βk,Bn∈Βn, 其中k 证明因为H∈Β2是Bn的成分子图,所以由定义可知存在Bn的成分子图序列G0∈Β2,G1∈Β3,…,Gn-3∈Βn-1使得(…(((H⨁G0)⨁G1)⨁G2)⨁…)⨁Gn-3=Bn。设H1=H⨁G0,H2=H1⨁G1,…,Hn-2=Hn-3⨁Gn-3=Bn,显然,H是Hi的子图且对任意的1≤i≤n-2,V(T)⊆V(Hi),因为H1=H⨁G0,所以 |NH1(V(T))|=|NH(V(T))|+|V(T)|。 类似地,我们有 |NH2(V(T))|=|NH1(V(T))|+|V(T)|, … |NHn-2(V(T))|=|NHn-3(V(T))|+|V(T)|。 考虑g=1的情形。设V(T)={x1,x2},下证G不包含孤立点。否则,假设u是G中的一个孤立点。从而,NBn(u)⊆NBn(T),即NBn(u)⊆NBn(u)∩NBn(T).由引理8(3)可知cn(Bn)=2, 故6≤n=|NBn(u)|=|NBn(u)∩NBn(T)|≤4矛盾。因此,G中不含孤立点。因此,此时NBn(V(T))是一个R1-割。 考虑g=2的情形。设T=P3=x1x2x3,下面首先证明G不包含孤立点。反之,假设G包含孤立点u.引理8和引理9(1),我们有6≤n=|NBn(u)|=|NBn(u)∩NBn(P3)|≤4, 矛盾。因此G中不含孤立点。若G中包含一条孤立边K2, 则由引理8,引理9(2)和n≥6, 我们有10≤2n-2=|NBn(K2)|=|NBn(K2)∩NBn(P3)|≤7,矛盾。因此,此时NBn(V(T))是一个R2-割。 观察1设T=K1,3∈Q3或T是G(8,4)中的一条路xyzw,如图5所示,则 |NB3(T)|=3。 图5 Q3和G(8,4)的子图T 引理11设H∈Β3是n维BC图Bn的成分子图,其中n≥6, 且设T是H的子图使得当H=Q3时,T≅K1,3;否则,设T=xyzw如图5(b)所示,则|NBn(V(T))|=4n-9且NBn(V(T))是一个R3-割。 证明因为H∈Β3是n维BC图Bn的成分子图,所以由定义可知,存在成分子图的序列G0∈Β3,G1∈Β4,…,Gn-4∈Βn-1使得(…(((H⨁G0)⨁G1)⨁G2)⨁…)⨁Gn-4=Bn。设H1=H⨁G0,H2=H1⨁G1,…,Hn-3=Hn-4⨁Gn-4=Bn,显然,H是Hi的子图且对任意的1≤i≤n-3有V(T)⊆V(Hi)。 因为H1=H⨁G0,所以|NH1(V(T))|=|NH(V(T))|+|V(T)|。同理,|NH2(V(T))|=|NH1(V(T))|+|V(T)|,…,|NHn-3(V(T))|=|NHn-4(V(T))|+|V(T)|。将前面各式依次迭代相加可得,|NHn-3(V(T))|=|NH(V(T))|+4(n-3)。由观察1,我们有|NBn(V(T))|=4n-9,令G=Bn-CBn(V(T))。 下证G中不含孤立点、孤立边和孤立的路P3。 因为n≥6所以|V(G)|=2n-(4n-9)>0, 从而G非空。假设G中包含一个孤立点u,则由引理8和引理9(3)和(4)可得,6≤|NBn(u)|=|NBn(u)∩NBn(T)|≤5,矛盾。因此,G中不含孤立点。 现在,假设G中包含一条孤立边K2,由引理9(5)和(6),有10≤2×6-2≤|NBn(K2)|=|NBn(K2)∩NBn(T)|≤9,矛盾。因此,G中不含孤立边。 最后,假设G中包含一条孤立路P3,此时,我们分两种情况进行讨论。 情况1n=6。 因为B6是6-正则的且cn(B6)=2,所以|NB6(P3)|=3×6-5=13。再由引理9(7)和(8),我们有13=|NB6(P3)|=|NB6(P3)∩NB6(T)|≤12,矛盾。 情况2n≥7。 因为Bn是n-正则且cn(Bn)=2,所以|NBn(P3)|=3×n-5≥16。另一方面,由引理9(9)和(10),我们有|NBn(P3)|=|NBn(P3)∩NBn(T)|≤13,矛盾。 因此,NBn(T)是一个R3-割。证毕。 由定理3、4和引理12,我们可以推出Bn在PMC和MM*模型下的g-超条件诊断度。 表1 部分BC网络在PMC和MM*模型下的g-超条件诊断度,其中g=1,2,3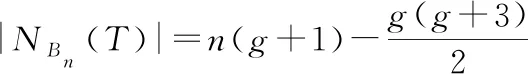





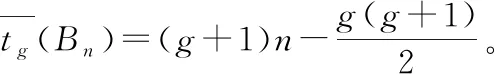

4 结论