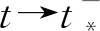
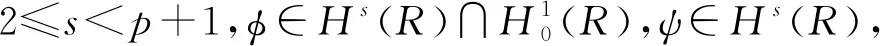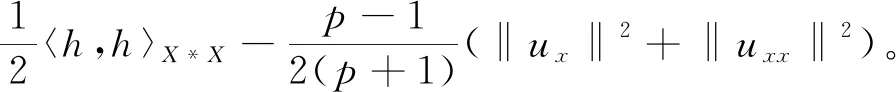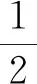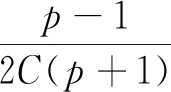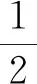具任意高的正初始能量的非线性六阶波方程解的爆破
2020-07-13郝江浩盖路路
郝江浩,盖路路
(山西大学 数学科学学院,山西 太原 030006)
0 引言
本文研究如下非线性六阶波方程的Cauchy问题,
utt-uxxtt-uxx+uxxxx+uxxxxtt=
r(|ux|p-1ux)x, (x,t)∈R×(0,T) ,
(1)
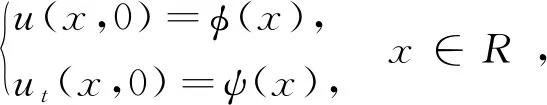
(2)
其中r≠0和p>1为常数,φ(x)和ψ(x)为给定初值。
这个模型可以用来描述许多物理过程,(1)是弱色散介质中非线性波动力学的通用模型(文献[1-2]),文献[3-4]研究了类似于(1)的浅水表面波的建模。并且方程(1)也被用于描述非线性晶格动力学中的模型。方程(1)的适定性已经被许多作者所研究,见文献[5-8]等。方程(1)是一般的Boussinesq方程,并且许多一般形式的Boussinesq方程已经被从不同的方面研究,见文献[9-15]。
Wang等[9]研究了问题(1)-(2)的Cauchy问题,通过使用压缩映射原理,证明了Cauchy问题(1)-(2)局部解的存在性和唯一性。在次临界初始能量(0 (φ,ψ)+(φx,ψx)+(φxx,ψxx)≥0 , 则解在有限时刻爆破,见文献[8,11]。 特别地,对超临界能量(E(0)>d)情形,相关文献较少,文献[12-13]证明了Cauchy问题(1)-(2)在高初始能量(E(0)>0)下解在有限时刻爆破,其中证明解的爆破性质是利用了Levine在文献[18]中给出的凸性方法。 我们研究Cauchy问题(1)-(2),将文献[8]中整体解的不存在性结果推广到任意高的正初始能量(E(0)>0)情形。通过文献[14]中给出的一种新方法,证明Cauchy问题(1)-(2)的解在任意高的正初始能量(E(0)>0),且初值满足一些结构性条件,则Nehari泛函I(0))必为负,进而可以利用凸性方法,得到相应的任意高的正初始能量的解在有限时刻爆破。 和 〈u,v〉X*X=〈u(·,t),v(·,t)〉X*X= (u,v)+(ux,vx)+(uxx,vxx)。 关于Cauchy问题(1)-(2)解的局部存在性结果,见文献[8]。 定理1设s≥1且φ,ψ∈Hs(R),则存在依赖于初值(φ,ψ)的最大存在时间T0,使得对每个T 对于系统(1)-(2),引入能量泛函 事实上,在(1)式乘上ut并在R上积分,有 (utt-uxxtt-uxx+uxxxx+uxxxxtt- r(|ux|p-1ux)x,ut)=0, 计算可得 即 所以,对于每个t∈(0,T0),有如下能量恒等式成立, E(t)=E(0) (3) 定义势能泛函 (4) Nehari泛函 (5) Nehari流形 Ν={u∈H2{0}|I(u)=0}, (6) 以及势阱深 ‖φ‖2+‖φx‖2+‖φxx‖2>0, (7) (φ,ψ)+(φx,ψx)+(φxx,ψxx)≥0, (8) (9) 则问题(1)-(2)的解u(x,t)在有限时间T*爆破。进一步,如果(φ,ψ)+(φx,ψx)+(φxx,ψxx)>0,则有爆破时刻的上界估计为 其中 L(t)=‖u(t)‖2+‖ux(t)‖2+‖uxx(t)‖2, C为某个正常数。 接下来,为定理2的证明做一些准备工作。关于函数u(x,t)+ux(x,t)+uxx(x,t),当‖u‖2+‖ux‖2+‖uxx‖2≠0时考虑ut的一个正交分解。首先,令 ut=ku+h, 其中(u+ux+uxx,h)=〈u,h〉X*X=0。经计算可知 因此有 (10) 从(10)以及u+ux+uxx与h的正交关系, 可以得到以下等式成立 (11) 即 ‖ut‖2+‖uxt‖2+‖uxxt‖2= 定义泛函 Q(t)=Q(u(x,t))= (12) 因此,能量泛函可以写成 (13) 这一节, 我们给出几个引理以及主要结果的证明。首先, 给出经典的凸性不等式。 引理1[18]假设F(t)是二次可微的正函数,满足对每个t≥α,其中γ>1和α>0是常数,有微分不等式 F″(t)F(t)-γ(F′(t))2≥0 都是严格增函数。更进一步,有L″(t)>0,以及 ‖u(t)‖2+‖ux(t)‖2+‖uxx(t)‖2≥ (‖φ‖2+‖φx‖2+‖φxx‖2)+ 2t((φ,ψ)+(φx,ψx)+(φxx,ψxx))。 (14) 证明当t∈(0,T],L″(t)=2‖ut‖2+2‖uxt‖2+2‖uxxt‖2-2I(t)>0,这说明L(t)是严格凸函数,且L′(t)是严格增函数。从(8)可知,当t∈(0,T]时,L′(t)>0。因此L(t)在t∈(0,T]上也是严格增函数。不等式(14)是L(t)凸性的一个结果。 当t∈(0,T]时,有 [(‖ut‖2+‖uxt‖2+‖uxxt‖2)· (‖u(t)‖2+‖ux(t)‖2+‖uxx(t)‖2)- I(t)(‖u(t)‖2+‖ux(t)‖2+‖uxx(t)‖2)- [(u,ut)+(ux,uxt)+(uxx,uxxt)]2]>0 . 由于I(u(t))<0且(u,ut)+(ux,uxt)+(uxx,uxxt)≥0,因此Q(t)在t∈(0,T]上是严格增函数。引理2证毕。 ‖uxt‖2+‖uxxt‖2), (15) 这里 证明由(3)和(11),对于解u(x,t)其中〈u,u〉X*X≠0有以下等式成立, (16) 首先验证I(0)<0,从(7),(8),(9)和(16)得到 即I(u(0))<0。 假设存在t0∈(0,T0), 使得当t∈[0,t0)有I(u(t))<0并且I(u(t0))=0。由引理2和式(3),(7),(9)及(16)有下列不等式成立, 因此I(u(t0))<0这与I(u(t0))=0相矛盾。所以,当t∈[0,T0), 有I(u(t))<0。 由引理2和式(3),(7)-(9),(14),(16)及Poincaré不等式可知存在一个t∈[tα,T0),使得下列不等式成立 (‖u(t)‖2+‖ux(t)‖2+‖uxx(t)‖2)- 引理3得证。 定理2的证明设T0是u(x,t)的最大存在时间。由引理2和(7),(8),有L(t)>0,L′(t)>0。利用Schwartz不等式,有 (L′(t))2≤4L(t)[‖ut‖2+‖uxt‖2+‖uxxt‖2] 由(15)式可得,对于每个t∈[tα,T0)有 L″(t)=2‖ut‖2+2‖uxt‖2+ 2‖uxxt‖2-2I(t)≥ (p+3)(‖ut‖2+‖uxt‖2+‖uxxt‖2)。 而有L(t)满足不等式 其中, 根据能量函数的定义知,L(t)≤E(t),因此由L(t)的爆破可知能量函数E(t)的爆破,即有问题(1)-(2)的解u(x,t)在有限时间T*爆破,且有爆破时刻的上界估计为 故定理2得证。1 准备工作和主要结论
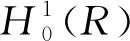

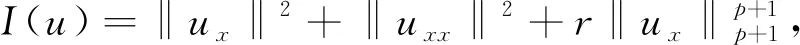
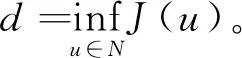
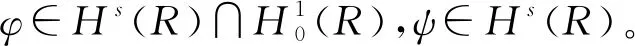
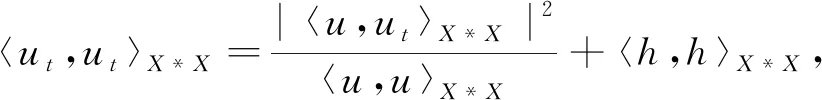
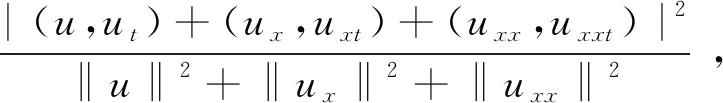

2 主要结论的证明