Contract theory based incentive mechanism design for buffer resource in wireless caching networks ①
2020-07-12LiuTingting刘婷婷TangLeiZhuHaoBaoYongqiangGuoYajuan
Liu Tingting(刘婷婷) , Tang Lei, Zhu Hao, Bao Yongqiang, Guo Yajuan
(*School of Information and Communication Engineering, Nanjing Institute of Technology, Nanjing 211167, P.R.China) (**Institute of Electric Power Science, Jiangsu Electric Power Co. Ltd., Nanjing 210024, P.R.China)
Abstract
Key words: contract theory, buffer resource allocation, wireless caching network, incentive mechanism design
0 Introduction
Due to the surge of duplicated transmissions in wireless networks, wireless caching technology has been proposed in order to release the transmission redundancy on backhaul channels[1-4]. The advantages of wireless caching technology have been provided as releasing traffic pressures on backhaul channels, reducing the transmission latency and improving the overall network energy efficiency, etc. The recent researches on wireless caching technology can be roughly classified into 2 aspects: content placement[5,6]and content delivery[7,8]. Most of these works have assumed that the popular files can be pre-cached into the edge nodes. However, due to the limited caching capacity, or the inaccurate estimation on user preference profiles, the requested files may not be cached or only be partially cached in the edge nodes. The transmissions of the un-cached files/parts may still induce the duplicated transmissions on backhaul channels or lead to transmission latency.
In order to further enhance the performance of wireless caching, researchers begin to investigate the joint buffer and cache allocations in wireless caching networks. Cache resource can be considered as a long-term memory to pre-cache the popular files during off-peak time. The pre-cached files can be directly transmitted upon requesting without triggering traffic on backhaul channels. Buffer resource is a kind of short-term memory. It can be used to store the fetched files from the remote servers or from the cache memory. Thus, it can be utilized to enable buffer-aided relay to improve the delivery performance of the un-cached files. Buffer usually has a high input/output (I/O) speed, and therefore, it is allocated with an expensive primary memory. In practice, due to the limited battery capacity, users usually have their personal use purposes or privacy concerns[9]. It is impossible for the edge node to contribute all its buffer resource. Generally, it will devote a limited buffer capacity to help transmissions. It is known that, due to users’ unbalanced data arrival and service rates, there may be some backlogs inside an edge or a relay node. In this paper, the edge node also acts as a relay node. The term ‘relay node’ is used for the ease of discussions. Backlogs may lead to queueing delay, and backlog overflow which is induced by the limited buffer capacity, and even induce re-transmissions over backhaul channels. How to allocate the limited buffer capacity to maximize relay node’s utility has become a critical issue in realizing the buffer-aided relay in wireless caching networks. At the same time, users are willing to utilize the buffer-aided relay scheme to enhance its transmission performance. How to design a proper incentive scheme to incentivize users in participating buffer-aided relay communications has also become an important issue. In order to solve the above 2 issues, 2 problems need to be figured out.
First, the relationship among the arrival rate, the service rate, the backlogs, and the buffer capacity should be determined. In this way, the buffer capacity on relay node’s side can be linked to each user’s backlogs which are determined by this user’s arrival and service rates. The effective bandwidth theory is a useful framework to analyze the backlog performance of broad classes of arrivals[10,11]. However, it may lead to loose estimation for non-Poisson processes, and it is not realistic to assume user’s arrival or service data follow Poisson processes. At the same time, the martingale theory is proposed as an alternative in analyzing the backlogs, which is flexible and suitable for any kind of arrival and service processes[12]. A lot of works have demonstrated that the martingale theory can provide a tight bound compared with the real data trace. Moreover, the derived bound can be used as an objective function or as a constraint to further optimize the network performance[13-16]. Thus, in this work, the martingale theory will be used to determine the relationship among the arrival rate, the service rate, the backlogs, and the buffer capacity.
Second, in the concerned wireless caching networks, user’s specific parameters cannot be fully observed by the relay node. Information asymmetry exists in this scenario. The relay node only knows the set of user’s parameters, but it cannot observe the specific value of each user. Contract theory is known as a powerful tool in solving this kind of information asymmetry problem[17]. Most of the existing works on contract theory can be classified into 2 categories: one is adverse selection[18-21], and the other one is moral hazard[22,23]. The existing works have highlighted that solving the problem of asymmetric information in resource allocation is the major advantage of contract theory.
In this work, an incentive mechanism for buffer resource based on the contract theory in the wireless caching networks is designed. The proposed scheme can provide proper economic incentives to users. The main contributions of this paper are summarized as follows.
(1) A commercial wireless caching network is constructed, where user’s backlog violation probability is derived based on the martingale theory. Then, the utility functions of the relay node and the users are formulated.
(2) Contract theory is proposed to design the buffer resource allocation scheme between the relay node and the users. The users are classified into different types according to their distances from the relay node. Correspondingly, the relay node divides its devoted buffer resource into different portions, defined as quality. The optimal contract problem is then constructed in maximizing the utility of the relay node.
(3) Next, the conditions of a feasible contract are developed, and they are considered as constraints in the constructed optimization problem. In order to obtain the optimal contract, the constraints need to be reduced by several steps, which are also elaborated.
(4) Numerical results are provided to demonstrate effectiveness of the proposed contract theory scheme. Also, it can be found that in terms of maximizing the relay node’s utility, the proposed scheme is superior to the equally allocated scheme.
The remainders of this paper are organized as follows. The system model and the backlog violation probability derived from the martingale theory, as well as the utility functions of the relay node and users are presented in Section 1. The detailed incentive mechanism design steps based on the contract theory are elaborated in Section 2. Numerical results are presented in Section 3, and finally conclusions are drawn in Section 4.
1 System model
In a wireless caching network, instead of direct transmitting files from the base station (BS) to the users, as shown in Fig.1, a nearby node will be employed as a relay to enhance the delivery performance.
1.1 User’s data arrival model
A userUirequires a file. Data are transmitted using the buffer-aided relay scheme. Assuming that the bursty file amountai(k) for userUiarriving at the relay node at timekfollows a Markov-modulated on off (MMOO) process which has 2 static status [Π0, Π1]. On state Π0, there is no data arriving, i.e.,a(k)=0, while on state Π1,ai(k)=Rbits/s, andR>0. The corresponding state transition matrixTrais defined as
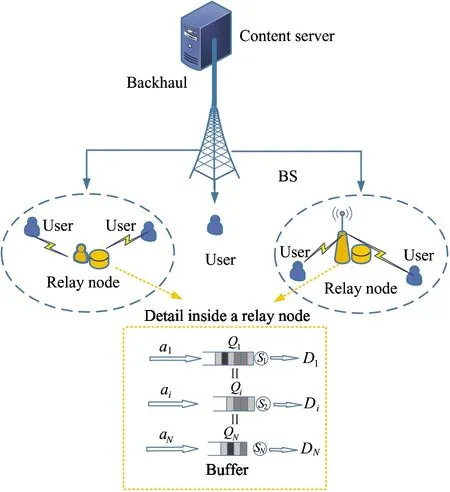
Fig.1 System model of a wireless caching network and the details inside a relay node
(1)
where,Tαrepresents the transition probability from state Π0to state Π1,Tβrepresents the transition probability from Π1to Π0. Accordingly, the steady state distribution ofai(k) is calculated as
(2)
Therefore, the cumulative arrival data over time interval [m,n] is represented as
(3)
where the unit of time interval is one second, andAi(m,n) can be regarded as a bivariate arrival process. Ifm=0,Ai(0,n)=Ai(n) is used for brevity.
1.2 Data service model
Assuming that the relay node devotes a buffer capacityCBto help the surroundingNusers relay their data. The transmission bandwidth isB. TheNusers equally share the bandwidth. A constant transmission powerPtris utilized for each user. According to Shannon’s channel capacity theorem[24], the service rate, i.e., the transmission rate, from the relay node to the user can be written as
(4)
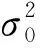
(5)
Note that when the user’s location is known, the service rate is irrelevant to timek.siis used for brevity.
Also, the following assumption is provided to make the analysis non-trivial.
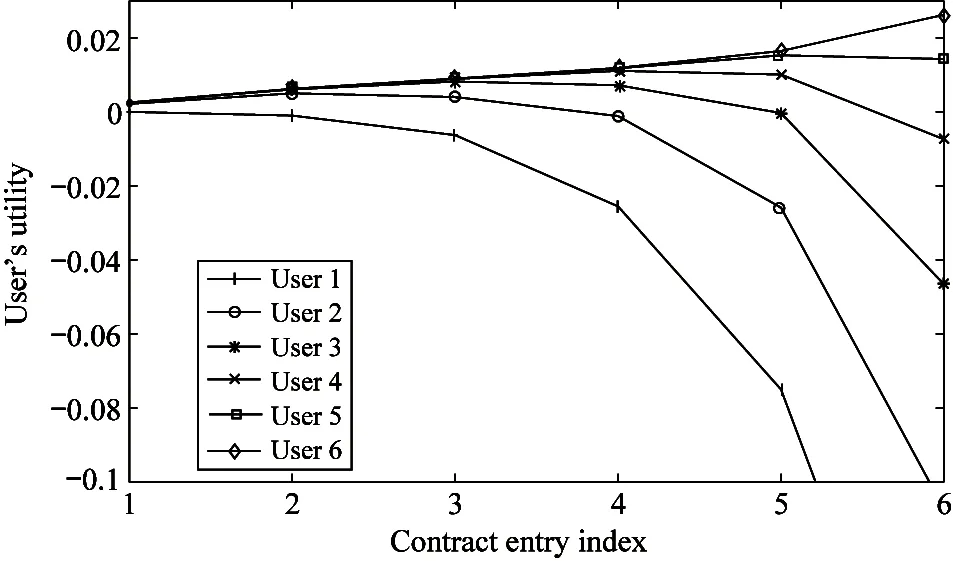
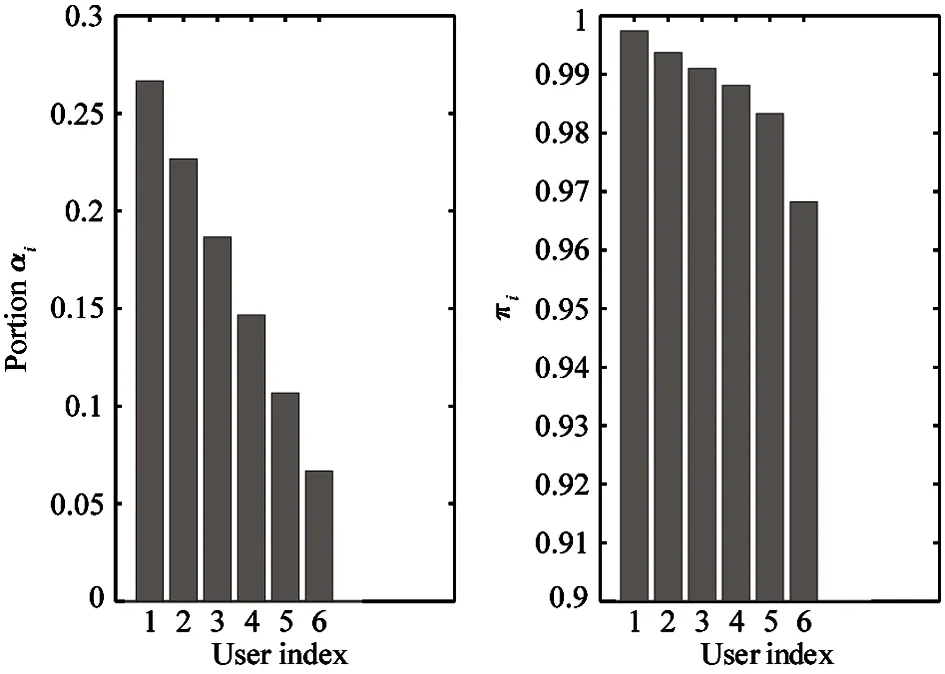
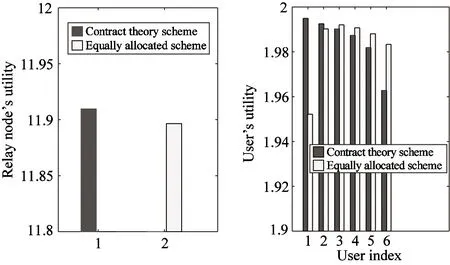
E[ai(k)] (6) Eq.(6) means that the service rate is larger than the average arrival rate, and it is smaller than the peak arrival rate. In this way, there will be some backlogs inside a relay node’s buffer. Since there are some backlogs inside a relay node’s buffer, i.e., (7) Definition1Backlog violation probability is the probability that a userUi’s allocated bufferαiCBis overflowed, i.e., Pr(Qi≥(αiCB)). (8) (9) The scheduling policy is first in first out (FIFO). Many works have contributed to derive the backlog violation probability. Here, it is provided directly in Theorem 1. Theorem1The backlog violation probability is calculated as (10) ProofPlease refer to Refs[12,14] for the rigorous deduction. (11) and Eq.(10) can be rewritten as (12) Assuming that a userUirents anαiportion, it needs to pay πito the relay node. If the data is overflowed, the overflowed data will be re-transmitted through the cellular link, and this will cost the userUiwith some extra money. The utility of the userUiis shown as follows. (13) (14) Relay node will make profits by renting out its buffer resource to the surrounding users. The relay node rents out anαiportion to the userUi, and correspondingly the userUiwill pay πito the relay node. Thus, the utility function of the relay node is represented as (15) The relay node designs the optimal contracts {αi,πi},i={1,…,N} to maximize its own profits. The optimal contracts also need to comply with the following 2 constraints: individual rationality (IR) and incentive compatibility (IC) for all intended users. The definitions of the IR and IC constraints are as follows. Definition3IR constraint: each user is assumed to be rational, and it will not accept a contract entry which produces a negative utility for its type. Therefore, IR constraint is provided as follows. (16) IR constraint means that the savings must compensate the payment. In the case ofUi<0, the user will not purchase the buffer portion. Definition4IC constraint: The incentive compatibility constraint means thatVvcannot gain more utility by accepting a contract entry which is not designed for its type. That is In other words, user with typeishould obtain the maximum utility if and only if it chooses the contract {αi, πi} designed for its type. The optimal contract problem aims to maximize the relay node’s utility, and also complies with the IR and IC constraints. Thus, the optimal contract problem is formulated as follows. (18) Contract theory is a kind of economical tool that can provide enough incentives to the users that motivate them choose the intended contract entry. This mechanism is guaranteed by the IR and IC constraints. That is to say, if users are not interested in paying anything, they will gain nothing, and if they do not choose the intended contract entry, they will not obtain the maximum profits. Since in Eq.(18), there areNIR constraints andN×(N-1) IC constraints. It is not tractable to solve an optimization problem with so many constraints. First, the number of constraints should be reduced by the following lemmas. 2.1.1 IR constraint reduction Lemma 1 is provided to reduce the IR constraint. (19) (20) 2.1.2 IC constraint reduction First, in order to make the analysis consistent with the contract theory. ‘Quality’ is defined in this paper. Definition5Since the buffer resource is considered as trading goods, the buffer portionαi,∀i, is defined as quality. The IC constraints can be reduced by the following lemmas. ProofLemma 2 is demonstrated from 2 aspects, i.e., sufficient condition and necessary condition. (22) and (23) Observing Eq.(22) and Eq.(23), then (24) Substituting Eq.(20) into Eq.(24), and after some manipulations, then (25) Eq.(25) can be rewritten as (26) (27) (28) (29) (30) This completes the proof. Moreover, if user’s utility function satisfies the local downward incentive constraint (LDIC) and the local upward incentive constraint (LUIC) simultaneously, the IC constraints will be satisfied. Furthermore, the LUIC can be derived from the LDIC, and vice versa. The IC constraints can be replaced by (31) By integrating the above lemmas, the original problem will be reduced to the following formulation. (32) By iterating IR and IC constraints shown in Eq.(32), the summation of πican be written as a general equation, i.e., (33) Substituting Eq.(33) into Eq.(32), the problem will be further reduced to the following brief formulation. (34) where, (35) It can be seen that eachCiin Eq.(34) is only related toαi. In other words, it is not coupled with otherαi. The first and second derivations ofCiare (36) and (37) respectively. It is easy to verify that Eq.(36)≥0, and Eq.(37)<0, Eq.(34) is a typical convex optimization problem. The optimal solution can be obtained by the interior point method. The numerical results are provided in the next section. In this section, numerical simulation results are presented to demonstrate effectiveness of the proposed scheme. The simulation settings are listed in Table 1. Some simulation parameters are assumed, for example,Tα,Tβ, user numbers,Ri, total bandwidth and buffer resource capacity. Some simulation parameters are commonly used, for example, the noise density and path loss exponent. The specific simulation settings will be elaborated if the simulation scenario is changed. Table 1 System parameters Fig.2 plots the variation of user’s utility when the user chooses different contract entries. It can be seen that each user will obtain the maximum utility when it chooses the contract entry intended for its type. For instance, user 1 will obtain the maximum utility when it chooses the 1st contract entry. User 2 can achieve the maximum utility in the 2nd contract entry. The 3rd contract entry can make user 3 get the maximum utility. Similarly, contract entry 4th, 5th, and 6th will provide user 4, 5, and 6 with the maximum utility, respectively. The incentive compatibility can be verified from Fig.2 that users cannot gain more utility by accepting a contract entry which is not designed for its type. Fig.2 The variation of users’ utility values when the user chooses different contract entry Table 2 The set of the parameter Fig.3 The optimal contract entry which is a combination of the optimal portion and the optimal price Fig.4 compares the utility of the relay node and the users between the contract theory scheme and the equally allocated scheme. The equally allocated scheme evenly divides the buffer capacity. It can be seen from Fig.4 that, the proposed contract theory scheme can achieve a larger utility compared to the benchmark scheme from the perspective of relay node. User’s utility decreases as user’s index increases when contract theory scheme is used. While this kind of trend cannot be observed when the equally allocated scheme is employed. Moreover, the user with index 1 has the maximum utility. This observation is consistent with the intuition that user 1 purchases the maximum portion and pays the most to the relay node, it should gain the most utility. On the other hand, as shown in Fig.4, the proposed scheme is superior to the equally allocated scheme from the perspective of relay node. The relay node who designs the mechanism will choose to use the proposed contract scheme. At the same time, users can obtain the positive utility by using the proposed contract scheme. Therefore, users would also be willing to participate in the proposed scheme. Fig.4 Comparison between the contract theory approach and the equally allocated scheme from the perspective of utility In this paper, the incentive mechanism incentivizing users in participating buffer-aided relay is investigated in wireless caching networks. Because of the information asymmetric environment, contract theory is utilized to design the incentive mechanism. Specifically, considering the limited buffer capacity, the backlog violation probability, i.e., the buffer overflow probability, is first provided based on the martingale theory. Based on the backlog violation probability, the utilities of relay node and users are formulated. Then, the optimal contract problem is modeled in order to maximize the utility of relay node, while the utilities of users are considered as IR and IC constraints. The feasibility of the contract is also demonstrated. Next, the optimal solution can be obtained by the interior point method. Numerical results are illustrated to demonstrate effectiveness of the proposed scheme. The proposed contract theory scheme has a better utility performance compared to the benchmarks.1.3 Backlog violation probability
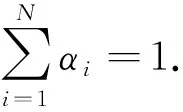
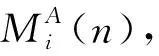

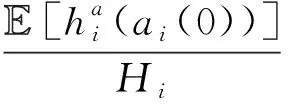
1.4 Users’ utility
1.5 Relay node’s utility
2 Incentive mechanism design based on contract theory

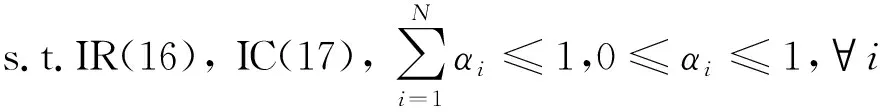
2.1 Constraints reduction
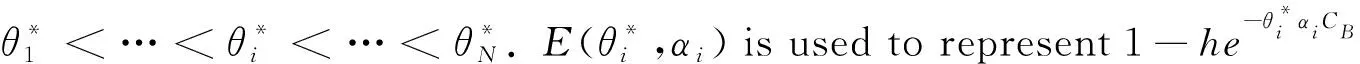

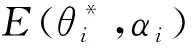
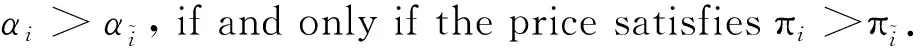

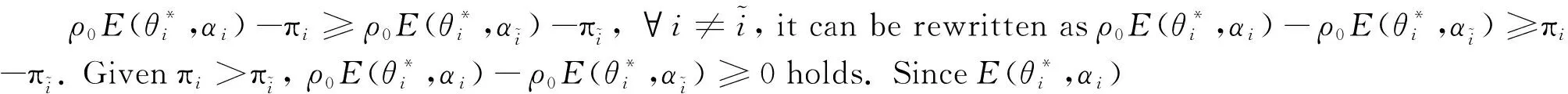
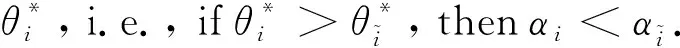
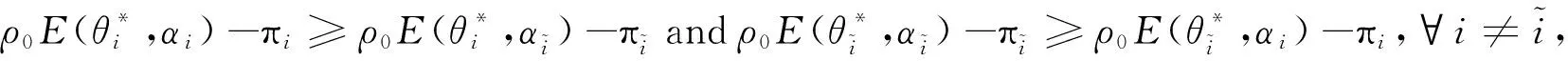
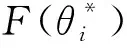
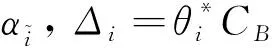

2.2 Optimal solution

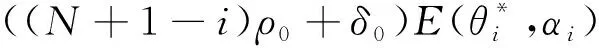

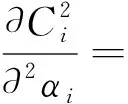
3 Numerical results
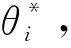
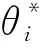
4 Conclusion
杂志排行
High Technology Letters的其它文章
- MW-DLA: a dynamic bit width deep learning accelerator ①
- Influence of velocity on the transmission precision of the ball screw mechanism ①
- Physical layer security transmission algorithm based on cooperative beamforming in SWIPT system ①
- GNSS autonomous navigation method for HEO spacecraft ①
- Control performance and energy saving of multi-level pressure switching control system based on independent metering control ①
- Improved image captioning with subword units training and transformer ①
