GNSS autonomous navigation method for HEO spacecraft ①
2020-07-12YuanDehu袁德虎SunJunHanFeiChenYangChenYun
Yuan Dehu(袁德虎) , Sun Jun, Han Fei , Chen Yang, Chen Yun
(* Shanghai Aerospace Control Technology Institute, Shanghai 201109, P.R.China) (**Shanghai Key Laboratory of Space Intelligent Control Technology, Shanghai 201109, P.R.China)
Abstract
Key words: global navigation satellite system (GNSS), high earth orbit (HEO), chaotic oscillator, autonomous navigation
0 Introduction
High earth orbit (HEO) satellites such as geostationary orbit (GEO) and high ellipse orbit satellites have important use in many fields, e.g. land and ocean communication, weather forecast, education application, television living broadcast, navigating and positing, data relay, disaster early warning, and space sun energy station. Therefore, HEO space tasks have increasingly become the research hotspots[1-4].
In order to satisfy the demand of space task, spacecrafts deployed on HEO need to decrease relying on the ground system. When the TT&C (tracking telemetry and command) system is in trouble or disturbed, the HEO spacecrafts should also keep survival and have the ability to perform the tasks. What’s more, the space task demands that the HEO spacecrafts can maneuver fast to the target neighborhood as in short time as possible, so as to implement acquisition and tracking of the target[5]. Hence, HEO spacecrafts need to have fast maneuvering ability. Due to the dynamic change of the system signal is huge, the navigation system should have good dynamic performance[6]. Therefore, autonomous navigation with high dynamic performance is very significant for HEO spacecrafts.
At present, HEO celestial autonomous navigation can not completely satisfy the demand concerning the precision aspect. The global navigation satellite system (GNSS) has been used in satellite orbit determination, because it has advantages such as high precision, no drift, no restriction by the TT&C station. However, it is mostly used in the orbit determination for low earth orbit (LEO) satellites. For those spacecrafts whose orbit height is above the GNSS satellites, the GNSS navigation system must consider the affection brought by poor coverage performance of navigation signal on HEO, small number of visible navigation satellites, and big transmission error of navigation signal. It also should have good processing ability for weak signal, and strong anti-jamming ability to steadily receive the GNSS signal[7-12].
In this work, acquisition and tracking of weak GNSS signal for HEO spacecrafts is implemented by adopting acquisition and dynamic detecting technology for weak signal using Duffing, on the basis of analyzing the transmitting and receiving error of GNSS signal. Related simulations are also carried out for demonstration.
1 Analysis of transmitting performance and error of HEO GNSS signal
According to the spherical symmetric principle, the general geometry relationship of occultation satellite is as follows.
The GNSS signal received by HEO satellites comes from the GNSS satellites on the back side of the Earth. The signal crosses the atmosphere or ionosphere, and related refraction may cause deflection of transmitting path. This will bring the transmitting time delay.
In most references, the transmitting deflection angle is evaluated by using GNSS Doppler frequency drift, then the transmitting delay of GNSS signal is estimated, ultimately it is deducted from the measured value of the pseudo range of GNSS signal[13-16]. Although by this method the transmitting delay of GNSS signal can be deducted, and the variation range of the transmitting delay can be obtained, it can not get precise time delay.
Because the positioning error of HEO GNSS signal mainly comes from the transmitting delay caused by the refraction of GNSS signal, the time delay must be compensated. Nevertheless, generally speaking, the time delay of GNSS signal is hard to be determined, so a general compensate method is adopted for the GNSS signal time delay.
1.1 Time delay range of GNSS signal
It is assumed that the position of a GNSS satellite isXG, the geocentric distance of the GNSS satellite isR1, the position of a HEO satellite isXE, the geocentric distance isR2, then it may yields:
S=|XG-XE|
(1)
(2)
Assuming the radium of the Earth isRe, then we judge that:
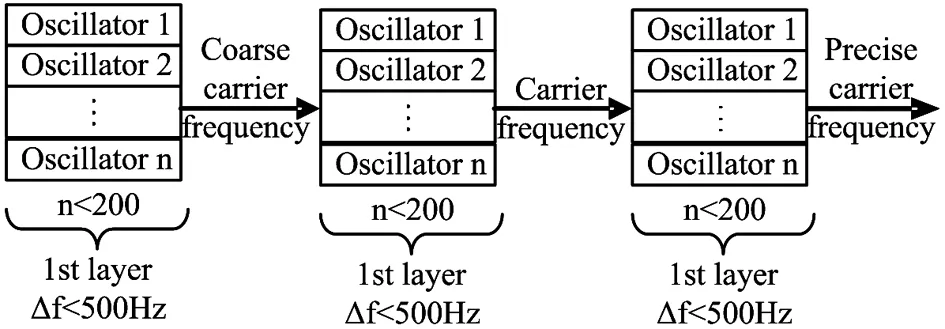
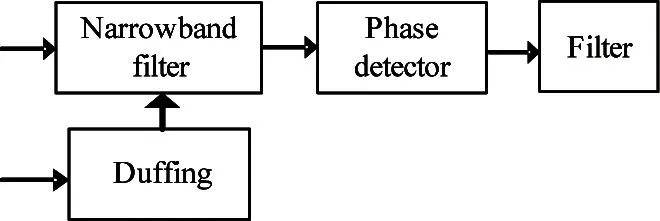
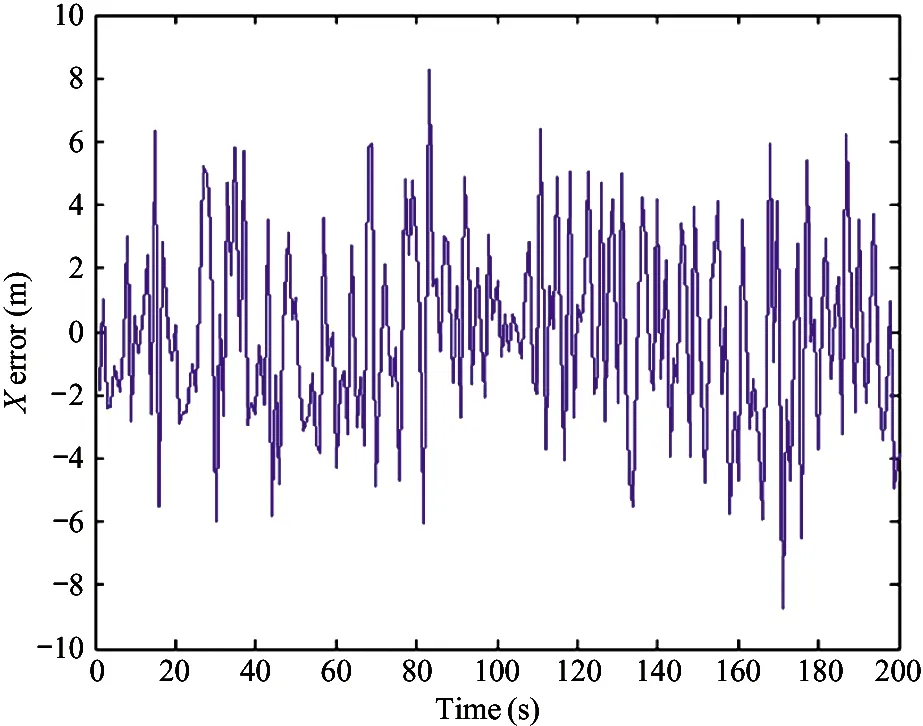
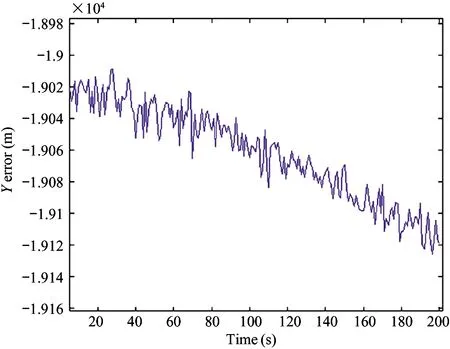
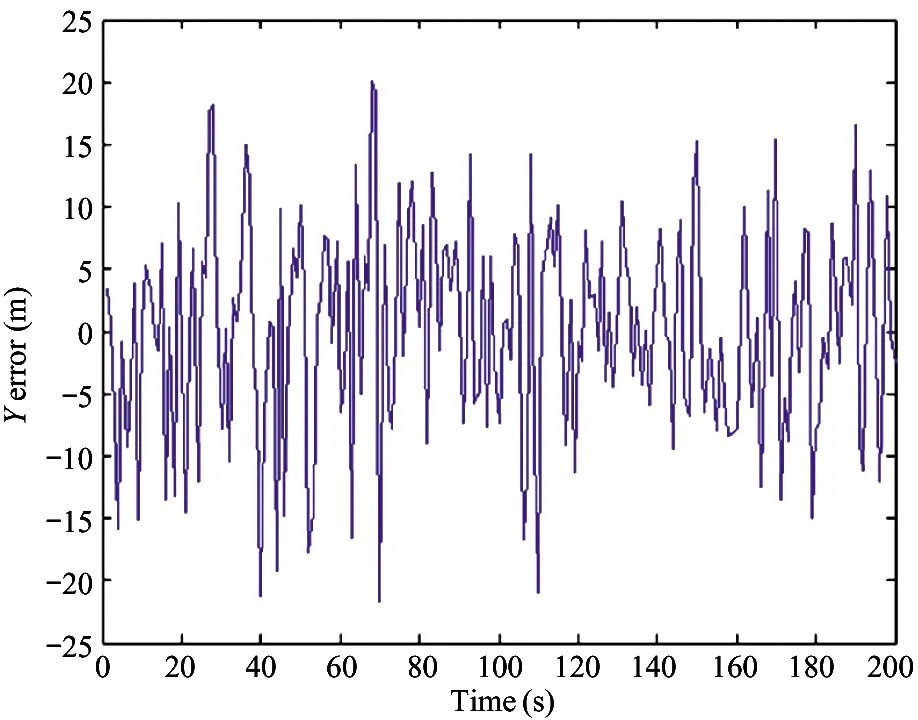
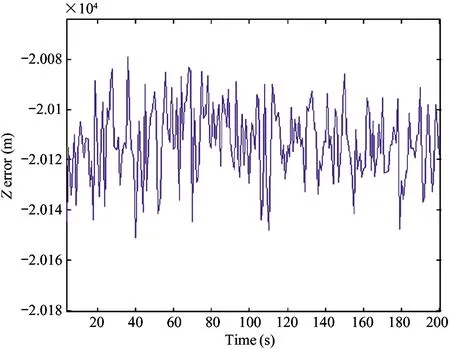
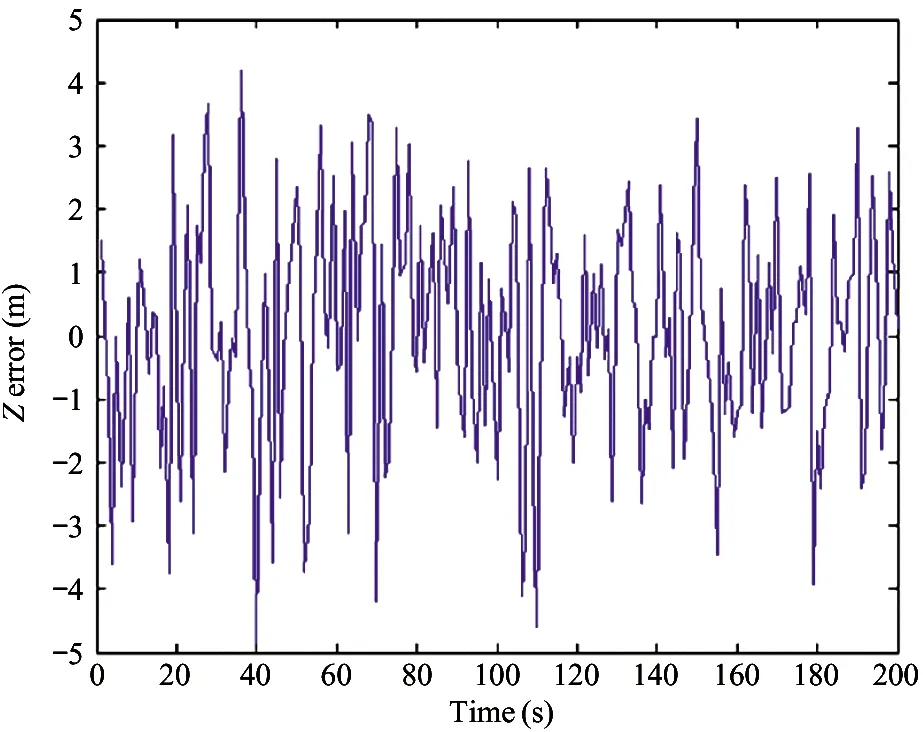
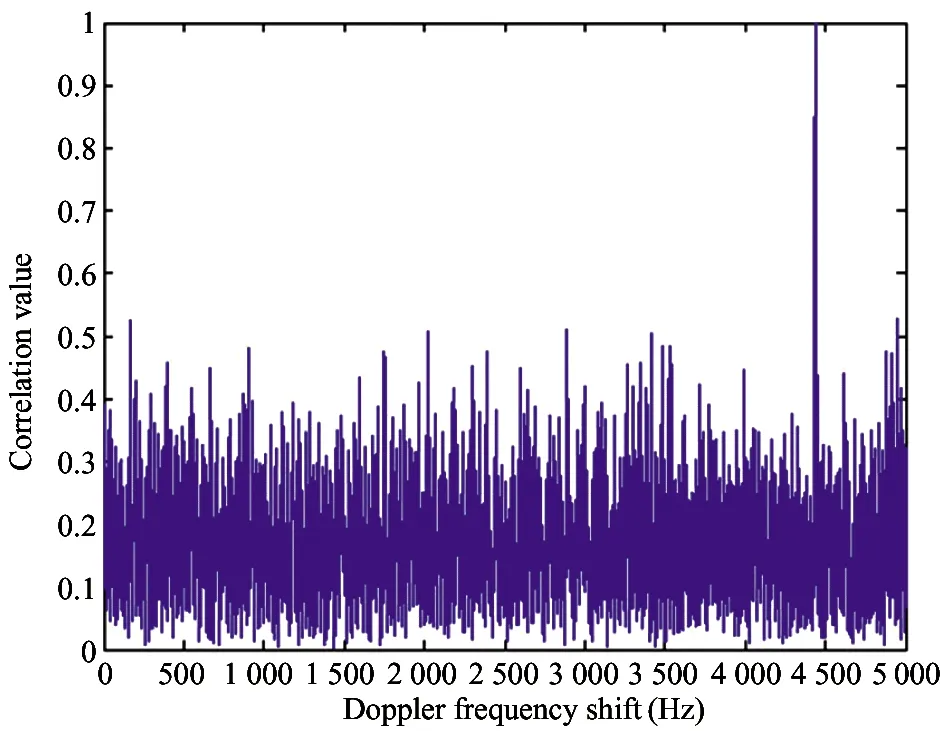
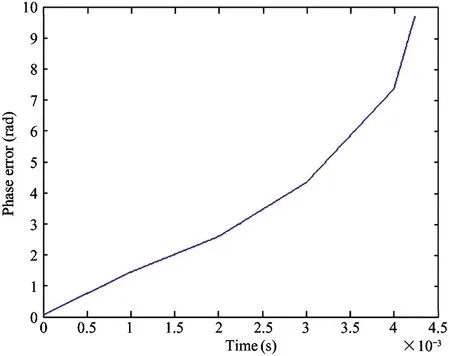
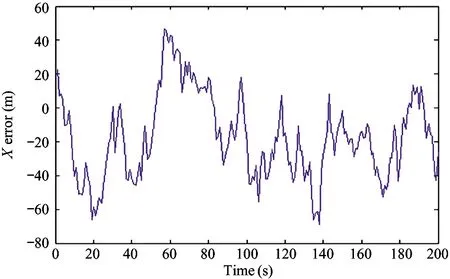
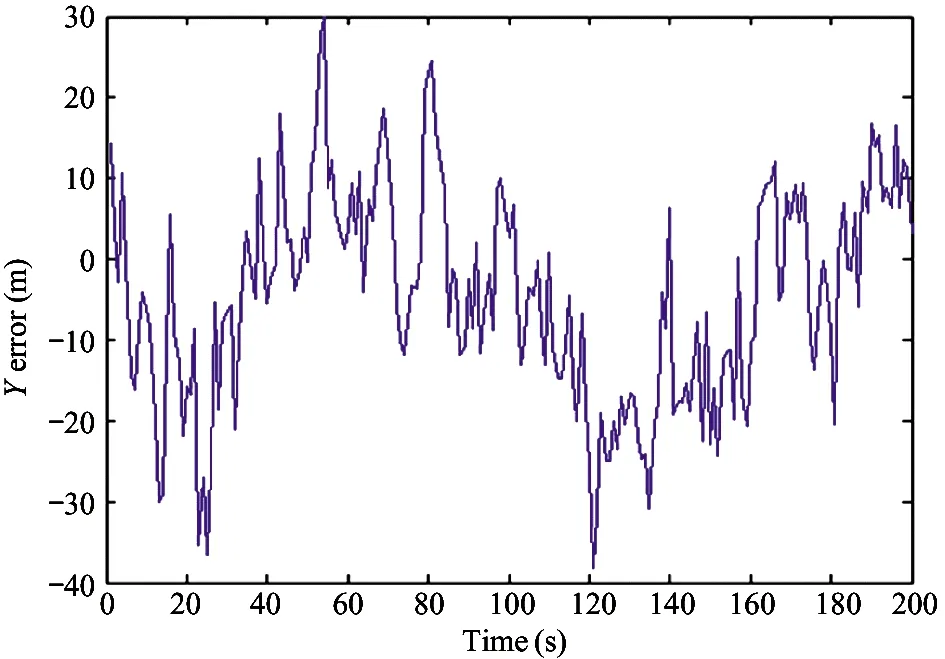
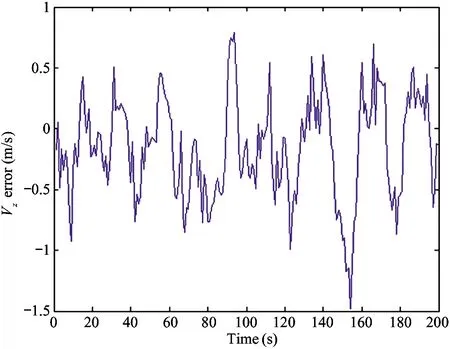
1) IfH Δ=Δmax (3) in which,Δmaxis the biggest transmitting time delay. Generally, it takes as 2 000 m. 2) IfH>Re, letΔH=H-Re, then the time delay is Δ=Δmax-kΔH (4) A certain valuekis chosen, makingΔ=0 whenΔH>hmax, in whichhmaxis the biggest height when the GNSS signal deflects. Assuming that the measured value of the pseudo range of the GNSS signal isρ, the iterative deduction withΔ0is set as the iterative step of the time delay compensation. The iterative times is chosen as (5) The pseudo range deduction is ρ=ρ-Δ0 (6) The judging principle is (7) Because the Duffing chaotic oscillator has great suppression effect on noises and it is very sensitive to periodical signal, so Duffing chaotic oscillator is adopted to detect weak signal. First of all, it needs to establish a chaotic system whose dynamic behavior is extremely sensitive to weak signal. Through adjusting the stimulating force, the chaotic system is under certain state. Then the detected signal is input to chaotic system. At this time, great changes of the state of the chaotic system will take place because of the joining of the input signal. The dynamic model is (8) If the detected signal is y=acos[(ω+Δω)t+φ]+n(t) (9) where the amplitudeais very small and the noisen(t) is very big. (10) Ifk=0.5 is chosen, then according to Melnikov method, the chaotic threshold value is obtained as (11) Therefore, whenrbecomes larger and larger from a very small value and passes through the above chaotic threshold value, for the system great changes will take place. It will run into big period from the chaotic state. Because there is great difference between the phase-plane loci of the chaotic state and that of the large-scale periodical state, the weak periodical signal can be detected by artificial or computational identification of the phase diagrams. It mainly detects the Doppler frequency when using Duffing oscillator to detect weak signal, so as to compensate the Doppler frequency change or to separate the Doppler frequency. For GNSS signal, because of the affection of data bit and code, the following detecting procedure is adopted, as shown in Fig.1. Fig.1 The Duffing detecting flow of GNSS signal For the acquisition of weak GNSS signal, it can be rapidly acquired by using the 1 time-domain method based on Duffing detection. In order to acquire the Doppler frequency with high resolution, hierarchical oscillator array is adopted to precisely acquire the weak signal, as shown in Fig.2. Using the hierarchical technology, carrier frequency of tens Hz can be precisely acquired. Fig.2 Hierarchical acquisition diagram If the coherent integration time is very long for the acquisition of the weak GNSS signal, the Doppler shift has great affection on the result. The number of FFT is of large amount, so the computation is very complex. In order to reduce the acquisition time, the following improvements can be made: 1) Hierarchical Duffing oscillator array is used to precisely detect the Doppler shift, which greatly reduce the frequency shift entering coherent integration (correlation computation) and decreases the affection of frequency shift. 2) Instead of using FFT computation, Duffing oscillator is adopted to precisely detecting frequency, which transforms a 2-dimension search into a 1-dimension one. 3) Differential computation is utilized to eliminate the affection of message upset, and the integration time can reach 20 ms, which greatly enhances the acquisition ability of GNSS signal and correspondingly improves the ability to suppress interference. The Duffing chaotic oscillator is used as the detector of signal tracking. Once the signal is acquired, the Duffing chaotic oscillator is locked. Through narrowband filter and tracking loop, precise tracking can be implemented. The tracking flow is shown in Fig.3. Fig.3 Tracking flow For the tracking loop of GNSS signal, the dynamic variation may cause the Doppler change, and furthermore the loop tracking precision may decrease or it will even be unlocked. Therefore, the precise tracking technology of high dynamic GNSS signal mainly lies in the compensation of high dynamic problem. For high dynamic GNSS signal, if there is no such outside assistant information as inertial navigation system (INS), or fault occurs on the outside inertial measuring unit (IMU), it is necessary to adopt the dynamic detection of inside signal, e.g. Doppler variation detection of high dynamic signal, to assist the loop filtering, thus the anti-dynamic ability of the loop can be increased. Exact description of mutual transforming relationship between different time systems and reference frames is important constituent part for precise orbit determination of satellites. The key step of multi-information fusion for multimode integrated navigation is space-time unification and search of relationship between different systems. The multi-information compatible processing method for multi-mode GNSS autonomous navigation system is as follows: take the clock synchronization error of different systems as the state variable of the integrated system for filtering estimation and space-time unification, estimate the clock error of different systems in real time, and implement soft synchronization. Therefore, in order to guarantee the time synchronization of different systems, the key problem for the combination of multi-system information is to guarantee that the number of visible satellites of multisystem must satisfy: 1) Bigger than 5 for two-system fusion; 2) Bigger than 6 for three-system fusion; 3) Bigger than 7 for four-system fusion. For navigation using GNSS, it needs at least 4 satellites to satisfy the basic navigation demand, so we choose 4 satellites whose geometric dilution of precision (GDOP) is small for the integrated navigation computation. In this study, optimal selection using GDOP is adopted. GDOP mainly describes the spatial geometric relationship of satellites. For 4 satellites, the GDOP value is of inverse ratio to the volume of the tetrahedron formed by the observation point and endpoints of unit vectors of satellites. When the tetrahedron volume attains maximum, the GDOP value is minimum. For HEO navigation, the satellite choice flow of GNSS constellation is shown in Fig.4. Fig.4 The satellite choice flow of GNSS constellation In order to improve the filtering precision and decrease the computation complexity,sequential filtering method are utilized in this paper. Firstly, take the pseudo range as measuring information for filtering amendment of position and velocity; secondly, choose the pseudo-range rate as measuring information for another filtering amendment of position and velocity. A GEO satellite is chosen as the HEO satellite[17]. The longitude of the GEO satellite is 115 ° east of Greenwich. GPS satellites are used as the GNSS ones. Iterative search method is adopted, in which the searching range is [0, Δ] and the termination condition isJ<1. The search scheme is that track the errorJ(k) and judge the convergent trend so as to minimize the iterative times. Assuming the transmitting delays are that, 300 m for No.1 satellite, 500 m for No.2 satellite, 200 m for No. 3 satellite and 2 300 m for No.4 satellite. The iterative step is 5 m. The simulation results are as following. 1) Error contrast ofXcoordinate 2) Error contrast ofYcoordinate 3) Error contrast ofZcoordinate From Figs 5-7, it can be seen that, if there is no time delay compensation, the orbit determination precision using GNSS signal would be very poor. When the time delay is about 2 300 m, the maximum position error would be about 21 000 m. However, after compensation for the transmitting delay, the position error is within 15 m, which shows that the compensation performance is very good and the compensation precision is very high. Thus, it can be seen that, the iterative compensation method by using occultation satellites judging to determine the search range can implement precise compensation. 4.2.1 Acquisition simulation It is chosen to receive the signal of 21st GPS satellite, and the signal noise ratio (SNR) is -45 dB. The coherent integration time is 200 ms and 400 ms respectively, and the non-coherent accumulation times are 3. The simulation curves are shown in Fig.8. It shows that the acquisition result is better when increasing the time of integration and times of non-coherent accumulation. 4.2.2 Tracking simulation The work uses 10 ms as the detection time of tracking loop to improve the carrier noise ratio (CNR) of the signal. It is assumed that the CNR of the weak signal is 17 dB-Hz, and the frequency shift running into tracking loop is 5 Hz. The third-order filter with second-order assistance is adopted, and the parameters are:ω0f=B/0.53,a2=1.414,a3=1.1,ω0p=B/0.7845,b3=2.4,P=2, whereBis the band width. The phase tracking result is shown in Fig.9. It can be seen that the tracking loop with 1 ms detecting integration time is out of lock, while that of with 10 ms detecting integration time can precisely track the weak signal. (a) Position error before compensation (b) Position error after compensation Fig.5X-coordinate error of the HEO satellite (a) Position error before compensation (b) Position error after compensation Fig.6Y-coordinate error of the HEO satellite (a) Position error before compensation (b) Position error after compensation Fig.7Z-coordinate error of the HEO satellite (a) The coherent integration time is 200 ms (b) The coherent integration time is 400 ms Fig.8Curves of correlation value for acquisition (a) The integration time of tracking loop detection is 10 ms (b) The integration time of tracking loop detection is 1 ms Fig.9 Phase error curves of tracking loop of weak signal Two constellation systems, i.e. GPS and BeiDou, are selected. The 5 satellites are No.1 GPS satellite with 1 000 m time delay, No.2 GPS satellites with 200 m time delay, No.3 BeiDou satellite with 300 m time delay, No.4 BeiDou satellite with 300 m time delay, and No.5 GPS satellites with 400 m time delay. The synchronization time error between GPS and BeiDou is 100 ns. The simulation results for position error are shown in Fig.10 and Fig.11. From the simulation results it can be seen that through integrated filtering the position precision and speed precision can be attained within 50 m and 1m/s respectively. Compared with middle-low orbit, in the HEO determination with GNSS, the number of visible satellites is very small, and there is little chance that no less than 4 satellites are visible at the same time. The transmitting distance is so far and the transmitting consumption is so large that the GNSS signal arriving to HEO is very weak. As for these problems, in this work, on the basis of analyzing the transmitting and receiving error of GNSS signal, related compensation scheme is proposed. Then acquisition and tracking of weak GNSS signal for HEO spacecrafts are implemented by adopting acquisition and dynamic detecting technology for weak signal using Duffing. At last simulation and related analysis are given. Simulation results demonstrate the feasibility and validity of the proposed scheme. (a) X-axis (b) Y-axis (c) Z-axis (a) X-axis (b) Y-axis (c) Z-axis1.2 Iterative solving
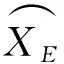
2 Acquisition and tracking method for weak signal
2.1 Detecting algorithm using Duffing chaotic oscillator
2.2 Acquisition technology using Duffing weak signal

2.3 GNSS tracking using dynamic detection
3 GNSS autonomous navigation combined with multi-constellation information
3.1 Multi-constellation optimal selection using GDOP

3.2 Filtering method of integrated navigation
4 Simulation
4.1 Simulation analysis of time delay compensation for HEO GNSS signal
4.2 Acquisition and tracking simulation of weak signal based on duffing detection
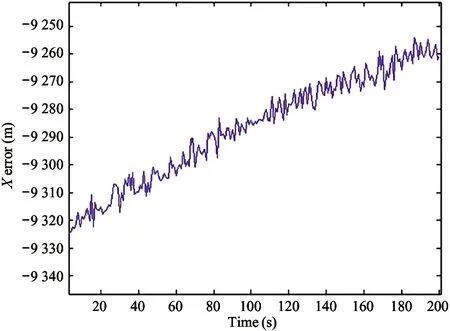


4.3 Autonomous navigation simulation
5 Conclusions



杂志排行
High Technology Letters的其它文章
- MW-DLA: a dynamic bit width deep learning accelerator ①
- Influence of velocity on the transmission precision of the ball screw mechanism ①
- Physical layer security transmission algorithm based on cooperative beamforming in SWIPT system ①
- Control performance and energy saving of multi-level pressure switching control system based on independent metering control ①
- Improved image captioning with subword units training and transformer ①
- RGB and LBP-texture deep nonlinearly fusion features for fabric retrieval ①
