Physical layer security transmission algorithm based on cooperative beamforming in SWIPT system ①

Wu Guodong(武国栋), Hu Zhentao , Jin Yong

(School of Computer and Information Engineering, Henan University, Kaifeng 475004, P.R.China )

Abstract

Key words: simultaneous wireless information and power transfer (SWIPT), beamforming, cooperative jamming (CJ), zero-forcing (ZF), secrecy communication

0 Introduction

Today, with the popularization of smart terminals and the increasing growth of wireless multimedia services, the information and communication industry is rapidly developing while its huge energy demand has become an urgent problem[1]. Traditional energy harvesting (EH) technologies (such as solar energy and wind energy) had many defects, and their EH efficiency was easily affected by weather, season and geographical condition, then they could not be a stable energy source for wireless devices. At present, a technique called simultaneous wireless information and power transfer (SWIPT) has been proposed, which can provide stable and controllable energy for wireless devices while transmitting the required information for them[2,3]. In addition, the application of SWIPT technology can reduce the hardware cost of the system and extend the service life of energy-constrained devices[4-6].

However, due to the openness of its communication mode, the transmission information of SWIPT is easily intercepted and monitored by illegal devices, so that the privacy of the information is difficult to guarantee[7]. The traditional security technology relies on the cryptography system, which mainly includes technologies such as identity authentication and key generation[8]. The effectiveness of the encryption algorithm is guaranteed by the extremely high computational complexity required to crack the key. But, with increasing computing power of computer, decoding efficiency of illegal user is gradually enhancing. Traditional encryption algorithm is facing new challenge.

Recently, physical layer security (PLS) technology has provided new ideas for researchers and gradually become a research hotspot[9,10]. Hoang et al.[11]considered a cooperative wireless network scene in which a source, a destination, and multiple intermediate energy harvesting nodes coexist with multiple eavesdroppers. By selecting a pair of intermediate nodes as a relay node and a jammer, confidential and jamming signals are respectively sent to the destination and eavesdroppers. Xing and Wong[12]explored information security transmission in SWIPT multi-relay network scene, and designed a cooperative beamforming scheme based on multi-relay cooperative jamming (CJ), and then gave a global optimal solution. Although the scheme can achieve excellent secrecy rate, the computational complexity of the algorithm is high.So, Xing’s algorithm is unsuitable in real-time engineering scene. Yang et al.[13]and Goel et al.[14]discussed the information security transmission problem of relay networks in single eavesdropping and multi-eavesdropping scenarios, and designed the corresponding low-complexity suboptimal schemes based on zero-forcing (ZF) criteria. The schemes transform the original non-convex problem into a convex problem by imposing a zero-forcing constraint on the eavesdropper, which significantly reduces the complexity of the algorithm. However, as the number of eavesdropper increases, the performance achieved by algorithm will deteriorate dramatically, and it will be difficult to meet the receiver’s need for secrecy rate. In addition, the algorithm is only suitable for the system in which the number of eavesdroppers is less than the number of relays.

In some practical engineering application scenarios, due to hardware limitations, algorithms are required to make reasonable compromise between computational complexity and performance. For this reason, a cooperative beamforming algorithm based on CJ and ZF is proposed in this paper. The core idea of the algorithm is to impose zero-forcing constraints on the capable eavesdroppers while suppressing the remaining weak eavesdropper using CJ method. Compared with CJ method, the proposed algorithm reduces the dimension of the target vector to be optimized, which leads to low computational complexity. Compared with ZF method, the proposed algorithm increases the spatial freedom of the target vector to be optimized and obtains high secrecy rate. The proposed algorithm has 2 advantages:

(1) Since the number of eavesdroppers who are imposed zero-forcing constraints in the algorithm is controllable, the computational complexity and performance of the algorithm implemented in this paper is also controllable, which is obviously more suitable for practical engineering applications.

(2) In addition, different from the work of Yang and Goel, the proposed algorithm does not limit the number of eavesdroppers, which is allowed to exceed the number of relays.

The rest of the paper includes 4 sections. Section 1 introduces the system model of the multi-AF (amplify and forward) relaying networks with SWIPT, and defines the secrecy rate of the relay wiretap channel. Next, through joint CJ method and ZF criteria, the secrecy rate maximization problem is formulated in Section 2, and an algorithm is designed to solve it. Then, Section 3 analyzes and evaluates the performance of the proposed method with others. Finally, conclusion is presented in Section 4.

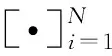
1 System model and problem formulation

This work considers the secrecy transmission of information in a multi-relay wireless sensor network with SWIPT as shown in Fig.1, which includes a source node S, a destination node D,Keavesdropper nodes Ek,k=1,…,KandNamplify and forward (AF) relay nodes Ri,i=1,…,N. And all nodes in the network are only equipped with a single antenna. In this network, the source node S hopes to establish stable secure communication with the destination node D by means of the relay nodes R. In addition, assume that there is no direct link between S and D, E for the simplicity of exposition.

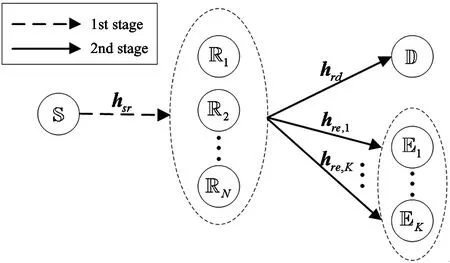
Fig.1 System model

Assume that each AF relay node lacks external power, it need to use the power split (PS) protocol to harvest energy and receive information simultaneously.Specifically, as shown in Fig.2, after the received signal of each relay passes through the power splitter, which split a portion ofρi,of the received power for EH, and the rest 1-ρifor information receiving.After that, the havested power is subdivided into 2 parts, whereγiof the power used for generating the artificial noise (AN) versus the rest 1-γiis temporarily stored in a capacitor and used to forward information later. Meanwhile, 0≤η<1 is defined as the conversion efficiency of energy harvesting.

According to the AF protocol, the cooperative process is divided into 2 stages.

1.1 Transmission stage

In the first stage,the received signal of each relay can be expressed as

(1)

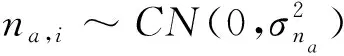
(2)

(3)

where ∠αiis defined as the phase of the AF coefficient of the relay Ri.

1.2 Cooperative forwarding stage

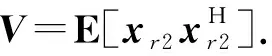
(4)

trace(VEi)≤ηγiρiPs|hsri|2,i∈{1,…,N}

(5)

where,Ei=diag(ei),eidenotes a unit vector withith element equal to 1 and the rest equal to 0.

The received signal at the destination D is given by

(6)

(7)

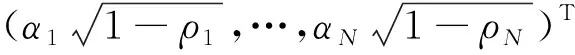
The received signal at the eavesdropper Ekis given by

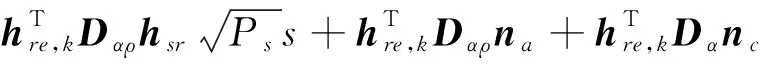
(8)

Thus, their respective signal to interference plus noise ratios (SINRs) are defined as

SINRS,D=

(9)

SINRS, E, k=

(10)

According to the SINRs, the mutual information for the destination D can be calculated asrS,D=0.5log(1+SINRS,D), and that for the eavesdropper EkisrS, E, k=0.5log(1+SINRS, E, k). In summary, the secrecy rate can be defined as

rsec=(rS,D-maxrS, E, k)+

(11)

2 The design of cooperative beamforming algorithm

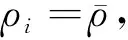
2.1 The preparation of beamforming

In order to analyze the problem conveniently, the Eq.(11) is transformed as:

(12)

(13)

and

i∈{1,…,N} (14)

again, by defining

(15)

and

i∈{1,…,N} (16)

that

rS,E, k=

(17)

Moreover, rewrite Eq.(5) as

i∈{1,…,N} (18)

2.2 The description of designed algorithm

Based on the priori information of the eavesdropper’s channel, the study considers first obtaining the signal to noise ratios (SNRs) of all eavesdroppers by the traditional cooperative beamforming (CB) method. According to that, the channel-related variables will be reordered from strong to weak. Then, it constrains the confidential signal to the null space of theK0strong eavesdropper’s channel while adopting the CJ method in the relay for the remainingK-K0weak eavesdropper.Note that the size ofK0directly determines the computational complexity and reachable secrecy rate of the algorithm.To illustrate the realization of designed method, the framework of the proposed algorithm is given in Fig.3.

Fig.3 The framework of the proposed algorithm

The purpose of this paper is to maximize the secrecy rate of the destination D by jointly optimizing the beamforming vectorωand the AN covariance matrixV. The corresponding optimization problem can be expressed as

(P1):

The details of the algorithm are shown in Table 1.

Remark: in Step 1, the traditional CB method is to makeK0=0 andV=0for the problem (P1).

2.3 The solution to (P1)

Since the objective function of (P1) is a non-convex function, a two-layer optimization method is introduced[11], and a slack variableφ∈(0,1] is added to recast (P1) into a joint problem of upper and lower layers. First, the lower-layer optimization problem can be seen as a quadratic programming (QP) problem with a given fixedφ, as follows.

(P1.1):

Table 1 The compromise algorithm

On the other hand, the upper-layer optimization problem is not only related toφ, but also to the optimal solution that can be obtained by the lower-layer optimization problem. Therefore,f(φ) is defined as the optimal solution of (P1.1). Meanwhile, we denoteH(φ)=φf(φ). The objective function of (P1) is expressed as

(19)

The above equation omits ()+in the original objective function. And we declare a zero secrecy rate when it is less than zero.

Therefore, the upper-layer optimization problem is described as

s.t.φmin,1≤φ≤1

Since the physical meaning of 1/φ-1 in (P1.1) is the maximum allowable SINR of the best eavesdropper’s channel[12], the feasibility of a non-zero secrecy rate means

(20)

Since anyφin the feasible domain can calculate the correspondingH(φ), and then the optimal solution of the upper-layer problem (P1.2) via a one-dimensional linear search in the interval [φmin,1,1] can be obtained.

Now, according to the zero-forcing criterion and the semi-definite relaxation (SDR) technique, we deal with the problem (P1.1).Specifically, letωCm, wherem∈CN-K0is an arbitrary vector,C∈CN×(N-K0)is a semi-unitary matrix consisting of an orthonormal basis for the null space ofk0∈{1,…,K0} which is arranged in rows. By introducingW=ωωH=CmmHCH=CMCHand ignoring the rank-one constraint ofW, (P1.1) is equivalent as follows:

(P1.1-SDR):

Note that the objective function has been multiplied byφto facilitate direct calculation compared with that of the optimization problem (P1.1).

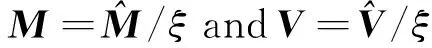
(P1.1-SDP) can be obtained:

It can be found that (P1.1-SDP) is a standard convex optimization problem, which can be solved by some convex optimization toolboxes.

3 Simulation and analysis

In this section, some simulation results are shown to evaluate the performance of the proposed algorithm.ConsiderNrelay nodes andKeavesdropper nodes randomly distributed in a circular area of radiusR=2 m, the source node S is fixed at the edge with a coordinate (-2 m, 0 m), and the corresponding destination node D is located at the position with a coordinate (2 m, 0 m). Furthermore, it is assumed that the channel model includes large-scale path loss and small-scale multipath fading.The unified path loss model is given byPL=10-3d-α, wheredrepresents the Euclidean distance between any two nodes.α=2.5 is the path loss exponent.In addition,hsr,hrdandhre,kare independent Rayleigh fading with zero mean andPLvariance.Other simulation parameters are set as shown in Table 2.

Table 2 Simulation parameters

Fig.4 shows the secrecy rate versus the number of unconstrained eavesdroppers. It can be found that the secrecy rate of the proposed algorithm is gradually increasing with the number of unconstrained eavesdroppers. Meanwhile, from the perspective of algorithm efficiency, the dimension of the beamforming vector to be designed will also increase with the number of unrestricted eavesdroppers, which will increase the computational complexity of the algorithm. Essentially, the number of zero-forcing constraints directly affects the degree of freedom (DoF), more DoF mean higher secrecy rate and computational complexity. This implies that the proposed algorithm can achieve a tradeoff between computational complexity and secrecy rate.On the other hand, it can be observed from Fig. 4 that the curve of the proposed algorithm is gradually flat, which indicates that the method of selecting the strong eavesdroppers is effective.In addition, the CJ method and the ZF method are the upper and lower bounds of the performance for the proposed algorithm, respectively. And the proposed algorithm is always superior to the traditional CB method.

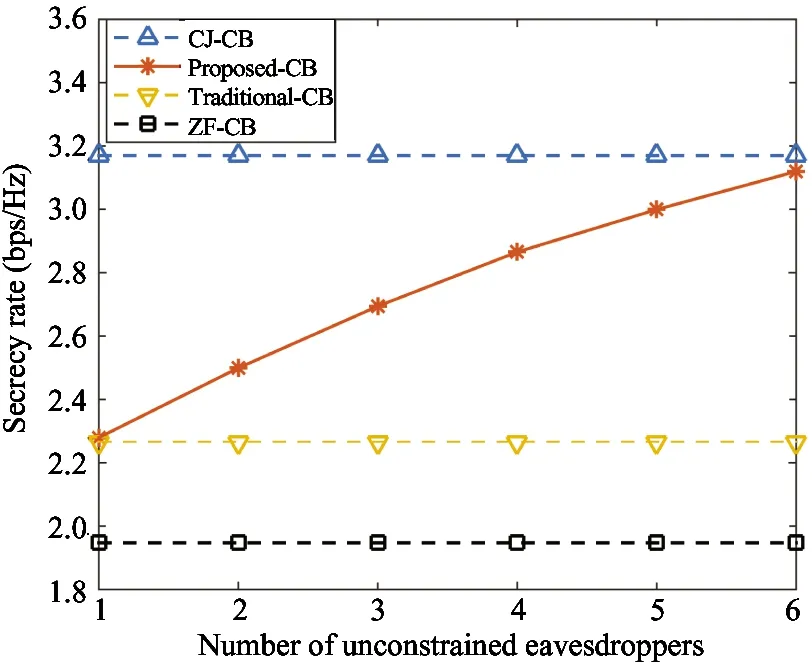
Fig.4 The secrecy rate versus the number of unconstrained eavesdroppers

Fig.5 shows the secrecy rate versus the number of relays. It can be seen that the proposed algorithm can always achieve a performance compromise. However, when the number of relays is large, the gap of the reachable secrecy rate of all 4 algorithms is not obvious. This shows that under the premise that the relay has more DoF, the system tends to suppress the eavesdroppers through CB instead of CJ. Therefore, if there are a large number of relays in the system, the number of constrained eavesdroppers should be increased. Obviously, avoiding these eavesdroppers with zero-forcing constraints can significantly reduce the computational complexity of the algorithm and have less impact on the secrecy rate.

Fig.5 The secrecy rate versus the number of relays

Fig.6 shows the secrecy rate versus the number of relays. It can be seen that the performance gap between the proposed algorithm and the CJ method remains approximately constant over the entire range of transmit power selection, which indicates that the proposed algorithm is stable to the change of transmit power. In addition, Fig.6 shows that in the low power phase, the secrecy rate of the algorithm is lower than that of the traditional CB method. Conversely, in the high power phase, the algorithm is superior to the traditional CB method. This is because when the transmission power of the source is low, the energy harvesting in the relay for CJ is too small, which makes the effect of the CJ not obvious, and the performance loss caused by the zero-forcing constraint cannot be compensated.

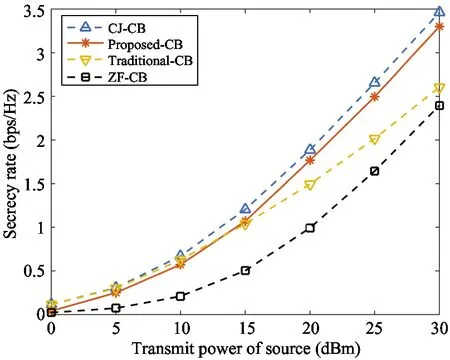
Fig.6 The secrecy rate versus the transmit power of source

4 Conclusion

In this work, a novel cooperative beamforming algorithm is proposed to balance performance of cooperative jamming method and zero-forcing method in multi-relay network with SWIPT. Different from the pure CJ method and the pure ZF method, the proposed algorithm achieves a controllable compromise between computational complexity and confidentiality rate by controlling the number of zero-forcing constraints. Finally, the simulation results prove the rationality of the algorithm. In the next research work, an adaptive threshold selection beamforming algorithm can be designed for the number of constrained eavesdroppers by analyzing different application scenarios.