MW-DLA: a dynamic bit width deep learning accelerator ①

Li Zhen(李 震), Zhi Tian* , Liu Enhe, Liu Shaoli*, Chen Tianshi *

(*Intelligent Processor Research Center, Institute of Computing Technology, Chinese Academy of Sciences, Beijing 100190, P.R.China) (**University of Chinese Academy of Sciences, Beijing 100049, P.R.China) (***Cambricon Technologies Corporation Limited, Beijing 100191, P.R.China)

Abstract

Key words: deep learning accelerator (DLA), per-layer representation, multiple-precision arithmetic unit

0 Introduction

With the rapid growth of data scaling and continuous improvement of hardware computing capability, the advantages of deep learning algorithms became more and more obvious than traditional machine learning algorithms. Recent studies showed that the recognition results are highly correlated with the depth of neural networks[1,2]. At present, in the field of image classifications[3,4], object detections[5,6], and semantic analysis, the effects of deep neural networks far exceed those of traditional machine learning algorithms.

However, deep neural networks demands more computation and memory resources than traditional machine learning algorithms. For example, AlexNet[7]requires 1.2 billion operations to process a picture. As a consequence, it is difficult to deploy deep learning neural networks in embedded systems which are power constrained and resource constrained. Therefore, designing an energy-efficient deep learning accelerator with limited resource is highly demanded.

Many previous work have made a lot of efforts to specialize deep learning computation paradigm in order to obtain higher performance power ratio. Chen et al.[8]proposed a scheme by using fixed-point data instead of floating-point data format, and combined with other optimization methods, realized a neural network processor with more than 100 times higher performance than the general-purpose processor, and the energy consumption is reduced by more than 30 times. Subsequently, Chen et al.[9]and Du et al.[10]realized the neural network processor applied to different occasions. The sparse neural network processor proposed by Zhang et al.[11]saved IO memory consumption by compressing weights. The sparse neural network processor proposed by Han et al.[12]focused on the weight compression technique. By removing invalid weights or the multiplication and addition operations of zero-value neurons, the total computational amount can be saved by 70%. The reconfigurable neural network processor proposed by Chen et al.[13]saved power by means of data multiplexing techniques and turning off the arithmetic unit when the input neuron value is zero. Brandon et al.[14]proposed a design space search method based on the analysis of neural network errors. By using fixed-point neural network data, pruning, and reducing SRAM power consumption, the average power consumption of the neural network processor is saved by 8.1x.

In this paper, a deep learning processor supporting dynamically configurable data-width, MW-DLA, is proposed. The contribution of this study includes:

• This work analyzes the difference of various data types in the same layer and the same data type through different layers in a neuron network. Then, this paper applies a dynamical method to quantify neurons and weights in different layers while maintaining the accuracy of networks.

• This research proposes a deep learning processor to support dynamic data-width.

• This research evaluates the performance and area overhead of the proposed processor relative to baseline design. The results show that this design can achieve high performance with negligible extra resource consumption than fixed point processors.

The rest of this paper is organized as following: Section 1 describes the background and motivation for MW-DLA. Section 2 shows the quantification methodology for training per-layer representation networks. Section 3 introduces MW-DLA. Section 4 evaluates MW-DLA, and compares MW-DLA’s performance and area with DaDianNao[9]. Conclusion is made in Section 5.

1 Background and motivation

The deep convolutional neural network (CNN) is a directed graph composed of a plurality of structures called neurons, and input layer neurons are mapped to output layer neurons by connections called weights. Neurons in each layers are arranged to multiple 2D matrices, each called a feature map. The feature maps in the same layer are of the same size. Typically, CNN includes a convolution layer for feature extraction, a local pooling layer for reducing the scale of neurons, and a full connection layer for feature classification.

The convolution layer uses multiple filters of the same size to perform feature extraction on the input layer to obtain different output feature maps. Each filter performs matrix multiplication with theKx×Kyrectangle receptive field on all input feature maps to obtain an output neuron. By sliding the filter’s receptive field by strideSxin thexdirection orSyin theydirection, a new output neuron can be computed. Thus the output feature maps are formed by traversing the input feature maps.

Similarly, pooling layer computes the average or selects the maximum one fromKx×Kyrectangle receptive field on one input feature map to obtain an output neuron on the corresponding output feature map. The whole output feature map is computed by sliding the receptive field on the input feature map. The scale of each feature map can be reduced by performing pooling on one layer of neurons while keeping the feature maps number unchanged.

Full connected layers are appended after a sequence of convolutional layers and pooling layers to classify the output categories of the input image. Full connected layer computes weighted sum of all neurons in input layer, and then performs active function on the weighted sum to obtain an output neuron. The weight vectors of different output neuron are different from each other.

Typically, the data of a network is represented in float32 or float16 format in general processor units. While float point arithmetic units are resource consuming and power consuming, Chen et al.[8]proposed using 16 bit fixed-point data instead of floating-point data format to achieve better performance and lower power consumption. Further, Patrick[15]pointed out that data from different layers can be layer-specified with little loss penalty. Motivated by Patrick’s work, this paper proposes a deep learning accelerator to support dynamic data-width with negligible extra resource consumption to achieve higher performance and better energy consumption.

2 Quantification methodology

In this paper, it takes a representative network of deep learning networks, AlexNet[7], for example. The network is trained on Caffe[16]framework. And the out of sample error is less than 0.1%. For each layer, weights and input neurons are converted to fix-point representation and then back to float format to feed them to obtain output neurons.

Per-layer representation network are obtained by fine tuning the pre-trained model downloaded from the Caffe model zoo[17]. First, this work chooses a set of quantification configuration for each layer. Then a two-phase termination method to fine tune the network at each iteration is used. In the first phase, neurons and fine-tuned weights are obtained using BP algorithm.In the second phase, decreasing the bit width of neurons or weights on the precondition of maintaining the accuracy within manageable proportions. Fine tuning terminates when the accuracy on validation set against no-quantified model exceeds 0.1%. After iterations, the resulting quantification configuration as Table 1 shows is obtained.

Table 1 Quantification configuration of AlexNet

3 MW-DLA

The above results indicate that the dynamical quantization of neurons and weights between different layers can be exploited to implement deep learning processor with higher performance and better power consumption. This section introduces MW-DLA, a deep learning accelerator which reduces memory bandwidth requirement and memory traffic simultaneously to improve processing performance of deep learning networks.

The proposed MW-DLA is an extension scheme of DaDianNao, a multi-tile DNN accelerator using uniform 16 bit fixed-point representation for neurons and weights. MW-DLA takes advantage of layer-wisely quantified neurons and weights to save memory bandwidth and storage as well as improve computing performance. To convey the mechanisms of MW-DLA clearly, Section 3.1 introduces the baseline accelerator, and the followed sections describe how to incorporate it with per-layer data representation to achieve higher performance and lower power consumption.

3.1 Baseline accelerator architecture

This paper takes DaDianNao as the baseline accelerator, which is organized in a tile-based form as shown in Fig.1(a). There are 16 neural functional units (NFU) in DaDianNao. All the computations of output layer are split in 16 segments of the same size to conduct on 16 SIMD NFU tiles.

Fig.1(b) shows the architecture of an NFU. DaDianNao uses massive distributed eDRAMs which is called SBs to store all weights closed to NFU to save power consumption of weights reading. There are also eDRAMs to buffer input neurons and output neurons in each tile, namely NBin and NBout. During every cycle, 16 elements of 16-bit input neurons and 256 elements 16-bit weights are read from NBins and SBs separately by NFUs. Then NFUs conduct matrix multiplication to obtain partial sums for the 16 output neurons. These calculated 16 elements of 16-bit output neurons are written to NBout when their corresponding partial sums are accumulated.

(a) Tile-based organization of DaDianNao

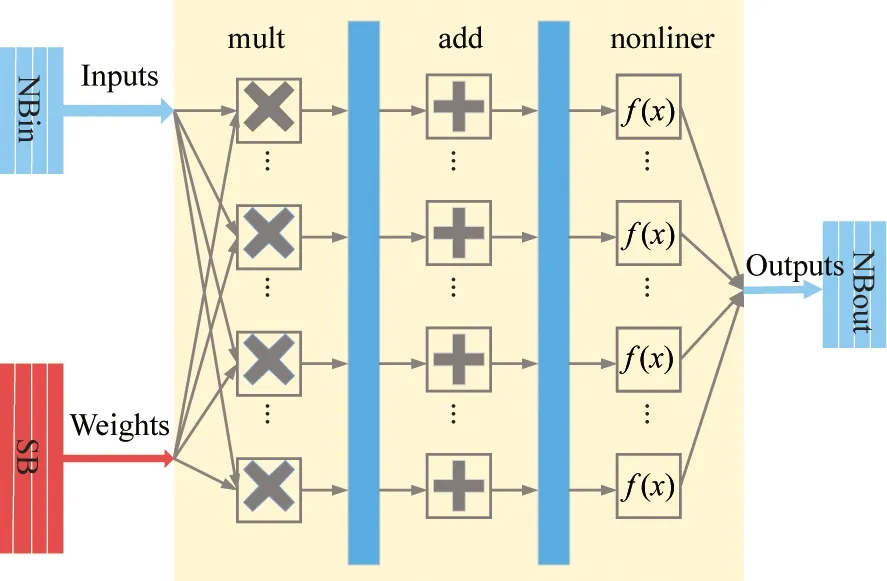
(b) Block diagram of NFU

Since DaDianNao stores the full copy of input neurons in a central eDRAM, an internal fat tree is applied to broadcast identical neurons to each tile, and to collect output neurons of different values from 16 tiles. The central eDRAM consists of 2 banks, each bank performs the roles of NBin and NBout similar to that in NFUs. Input neuron vectors are broadcast to all tiles for different output neurons. Since the computation of an output neuron usually takes more than 16 cycles, these output neuron vectors can be collected from different tiles in time division multiplexing manner with no performance penalty.

3.2 Memory layout

Since the data width of input operating elements is uniform for all networks, the memory layout can be simplified as shown in Fig.2(a). Weights feeding to each NFU in every cycle are arranged in the same line in SB. Each NFU reads weights with line index according to the expected execution order. In this case, SB

memory is designed to provide one group weights with equal size every memory accessing. Similarly, each group neurons in NBin, NBout and central eDRAM are arranged in the same line. Whereas a group of weights consists of 256 weight elements and a group of neurons consists of 16 neuron elements.

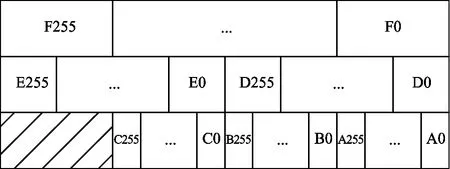
The input operating element width can be different for each layer since the quantification width of neurons and weights varies between layers. The data size of a group weights varies if there are various data representations with different bit width. Meanwhile, a group weights can start at any arbitrary position of a line in memory if the input operating element width ranges from 1 to 16. In addition, the execution engine cannot read weights as a data stream from SB simply accumulating the address because weights would be reused many times while NFUs are conducting convolutional layers. As a consequence, it would be a challenge to feed weights to NFUs.

Considering the quantification width of both neurons and weights can be ranged from 1 to 16, the situation would be more complex for execution engine to feed NFUs with neurons and weights. To resolve this problem, MW-DLA supports bit-widths of 2, 4, 8, and 16 in memory and the inputs of NFUs. This work applies the following methods to determine the input operating element width and storage element width. Firstly, searching for the nearest supporting width which is larger than quantification width to the weight representation width in a layer to obtain weight storage element width. Then, storage element width for neurons is obtained by searching up the nearest supporting width to the neuron representation width in a layer. Finally, comparing the optimum widths and choosing the larger storage element width as the input operating element width for the certain layer.

(a) Memory layout in DaDianNao

(b) Memory layout in MW-DLA

As Fig.2(b) shows, there can be 1, 2, 4, and 8 groups of weights in a memory line depending on the data-width.Ngroups of weights and neurons are fed to a NFU on every cycle. ParameterNis obtained by dividing 16 with input operating element width. Weights for each layer are aligned to memory storage line size to avoid weights for one input batch to a NFU spreading over two memory lines. In this case, MW-DLA reduces the footprint of memory with negligible extra hardware cost.

3.3 Multi-precision multiplier

MW-DLA adopts multiple-precision multipliers to achieve higher performance. Multiple-precision multipliers are capable of conducting more multiplication operation for input operands with shorter data-width.The multiple-precision multipliers in NFUs support 2, 4, 8, and 16 bit. Correspondingly each NFU is able to conduct 2 048, 1 024, 512, 256 times multiplication on every cycle.

Fig.3 shows a common structure for a fixed-point multiplier. It roughly contains 3 stages. In the first stage, a radix-4 booth encoder scansN-bit operand X and Y to generateN/2 partial products. Radix-4 booth algorithm encodes continuous 3 bits in Y with a stride of 2 bits to 5 possible partial sums 0, -X, +X, -2X, and +2X. In the second stage,N/2 partial products are fed to a Wallace reduction tree for compression to obtain 2 operands. In the third stage, the two operands are added by a carry-look-ahead adder to obtain the final multiplication result.

Fig.3 Multiplier architecture block diagram

This work adopts the concept of shared segmentation[18]to implement multiple-precision multiplier. Since the width of outcome and partial products of multiplier is positive ratio to the input operand width, there is possibility to reuse the logic to support multiple precision in the same multiplier. A detailed example is shown in Fig.4 and Fig.5. There are 4 16-bit partial products when the input operands is 8 bit width. While partial products are split into 2 groups, each group contains 2 8-bit partial products, when the input operands is 4 bit width. A Wallace tree consisting of 16 4-2 Wallace carry-save adders(CSAs) can be used to reduce 4 partial products for 8 bit operation as shown in Fig.4, and can also be used to reduce into 2 groups partial products respectively for 4 bit operation as shown in Fig.5. When conducting 4 bit multiplication, the carry bits from the seventh CSA (CSA_7) to eighth CSA (CSA_8) are disconnected.

Fig.4 Booth partial product array for 8×8 bit multiplication in 8 bit-mode

Fig.5 Booth partial product array for 8×8 bit multiplication in 4 bit-mode

There are also efforts in first stage and third stage to fully implement multiple-precision multiplier. In the first stage, an extra mux is applied to select manner to generate 4 non-zero partial sums, and then reuse the radix-4 booth encoder to obtain partial products. The position of generated partial products are arranged in that they are compressed in Wallace tree. In the third stage, there are 7 extra 2-input ‘and’ gates to kill the carries which pass across the element boundaries.

3.4 Multiple-precision add tree

The output partial sums from multi-stage are divided into 16 groups corresponding to computing 16 output neurons in add-stage. Each group partial sums are added up by an adder tree. This paper uses a 16-input Wallace reduction tree followed by an adder rather than 15 adders to add up 16 partial sums in order to reduce logic and power consumption.

The adder tree also supports multiple precision inputs since there are multiple precision output partial sums from multi-stage. Similar to the multiple-precision multiplier, adder tree divides the input data into groups according to the operand type, and preferentially adds up input data of the same group. Each group contains 16 partial sums.

Fig.6 shows an adder tree supports operands for both 16-bit and 32-bit. Partial sums are extended by 4 bits with a sign bit to avoid data overflow. When input operands are 16-bit width, the lower 20 CSAs and lower 20 bits of CLA compute one group partial sums and the higher 20 CSAs and higher 20 bits of CLA compute another group partial sums. There are also ‘and’ gate to kill carries passing across bit 20 and bit 21 in Wallace tree and CLA.

Fig.6 Block diagram for multiple-precision add tree

3.5 Data packing and unpacking

The width of input operating elements might be different from the width of storage elements in neuron memories or weight memories. This paper applies a data unpacking unit shown in Fig.7(a) to convert theM-bit neuron/weight element read from memory intoN-bit elements for computation. A 256-bit register is used to store the weights or neurons read from memory. A row of neurons or weights from memory may be decompressed into multiple rows of data for computation sinceN=2k×M. Thus data unpacking unit does not read new weights/neurons from theSB/NBin on every cycle. In each beat 256/NM-bit elements from the 256-bit register are sign-extended toN-bit ones, then elements are shifted to obtain 256 bits of data feeding to a NFU.

When 16 output neurons are calculated by an NFU, a data packing unit shown in Fig.7(b) is used to convert the output neurons to reduced precision representation and pack them up.If the required bit width of output neuron isPand corresponding element width in memory isQ, the data packing unit convert output neuron intoQbit data-width and the data ranges in [-2p-1, 2p-1]. The data conversion equals to output neuron toP-bit data with data overflow handling, and then sign extending toQbit width. After data conversion, 16Q-bit elements is shifted and spliced by a shifter.

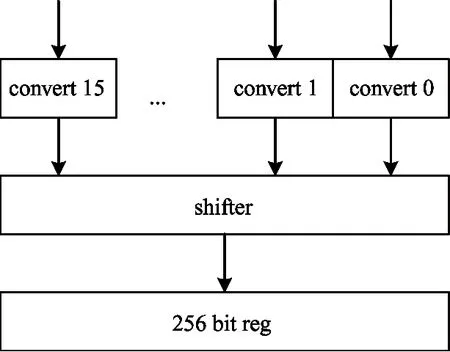
(b) Block diagram for packer

4 Evaluation

This section evaluates the performance and area of MW-DLA. It also compares MW-DLA with baseline design DaDianNao[9]. The comparison focuses on the execution of convolutional layers and full-connected layers, and the overall network performance of selected typical neural networks.

4.1 Methodology

Per-layerrepresentationnetworktrainingBy fine tuning the pre-trained model downloaded from the Caffe model zoo, per-layer representation network is obtained. Since the data format difference between Caffe and MW-DLA may cause the overall accuracy on validation set mismatch, this work modifies the data representation and arithmetic computation in Caffe. Firstly, neuron/weight is represented in fix-16 format, neuron/weight is quantized to specified bit width and then sign-extended to 16 bits. Secondly, partial sum and residual error are represented in fix-32/48 format. Thirdly, multiply and add operation are conducted using integer operand in forward phase. Table 1 reports the corresponding results.

PerformanceandareaMW-DLA differs DaDianNao in the implementation of NFU, while sharing the other parts. This work implements the NFU of MW-DLA and DaDianNao using the same methodology for consistency. A cycle accurate model is used to simulate execution time. Both design are synthesized with the Synopsys design compiler[19]with TSMC 16 nm library. The circuits are running at 1 GHz.

4.2 Result

PerformanceTable 2 shows MW-DLA’s performance relative to DaDianNao for precision profiled in Table 1. MW-DLA’s performance improvement is in proportion to the reduction of computation width. MW-DLA achieves 2X speedup for AlexNet.

Table 2 Speedup of MW-DLA relative to DaDianNao

MemoryrequirementTable 3 shows reports MW-DLA’s memory requirement relative to DaDianNao for precision profiled in Table 1. MW-DLA’s memory requirement is in proportion to the data-width of neurons and weights. MW-DLA reduces more than 50% memory requirement reduction for AlexNet.

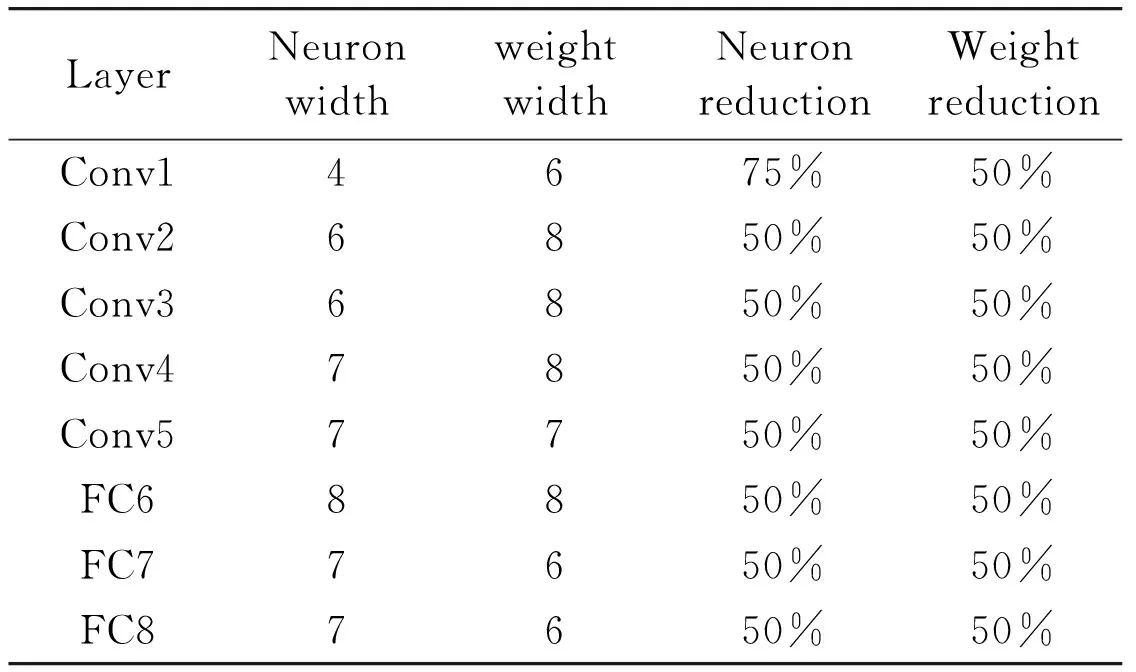
Table 3 Memory requirement of MW-DLA relative to DaDianNao

AreaoverheadAccording to the report of design compiler, MW-DLA requires 0.145 mm2for each NFU, while DaDianNao requires 0.119 mm2. MW-DLA brings 21.85% extra area consumption for each NFU. Considering the memory and HTs takes 47.55% and 26.02% area consumption of DaDianNao, MW-DLA brings at most 5.77% extra area consumption compared with DaDianNao.

5 Conclusion

MW-DLA, a neuron network accelerator supports per-layer dynamic precision neurons and weights, is proposed to achieve better performance and reduce the bandwidth requirement. The design is a modification of a high-performance DNN accelerator. According to the evaluated performance and area consumption relative to baseline design, MW-DLA achieves 2X speedup for AlexNet while bringing less than 5.77% area overhead.