基于特征挖掘的GRU-A光伏发电功率预测

张 进，刘 运，彭曙蓉

（1.陕西科技大学电气与控制工程学院，西安710021；2.长沙理工大学电气与信息工程学院，长沙410114）

0 引 言

光伏发电是可再生能源太阳能最重要的一种应用，截至2018 年底，全球总光伏装机量大于500 GW，2018 年全球新增光伏装机量约103 GW，其中，我国新增光伏发电装机量为43 GW，占2018 年全球新增光伏发电装机量的40%以上，中国已成为全球最大的光伏发电市场。光伏出力具有很大的随机性和波动性，大面积并网会对电力系统产生一定影响［1］。有学者提出，光伏发电系统的发电功率在电力系统总发电功率中占比的提高会使电网调度难度加大，当比例大于15%时，则会造成发电系统错乱的后果［2］。因此，对光伏发电功率的准确预测能够很大程度上解决光伏发电所带来的问题，使电网实现效率最大化。

国内外学者针对光伏预测已经做了较多的研究，主要的预测方法分为直接法和间接法［3］。直接预测法是根据光伏发电的历史数据和气象预测数据直接预测发电功率或发电量，直接法虽然预测过程简单但是考虑因素比较单一，预测的发电功率也不够精确；例如文献［4-5］中采用直接法构造了ARMA模型以及马尔科夫链模型预测短时间光伏发电功率，这种模型仅仅在晴天状况下的出力预测效果较好，适用条件太单一。间接预测法则是先根据相关数据预测出太阳辐照度，再通过某种算法来预测光伏发电功率或者光伏发电量，间接法的预测精度比直接法高很多，使用也越来越广泛。文献［6-7］中参考了相似日和相似时段光伏出力的基础上，对不同天气状况下的光伏出力预测搭建了BP 神经网络、Elman 神经网络和Spiking 神经网络模型，这些模型只适合于天气类型单一的日光伏出力预测，而对于1 d 当中历经多种天气变化情况的预测效果相对较差。文献［8］中进行光伏出力预测的方法选取的是灰度神经网络混合模型算法，对光伏出力有主要影响的因素纳入了考量范围，所得结果比单一模型好，但利用此模型进行预测时必须依照天气情况来划分子模型，实际适用效果较差；文献［9］中使用多种灰色预测模型相互结合的方式对光伏出力预测进行建模，但是因为未结合天气、温度、湿度等因素，预测的精度不是很好。文献［10-11］中建立了基于支持向量机的光伏预测系统，利用历史数据和气象数据按照统一建模和按时间顺序建模对光伏出力进行了分析与预测，将两种建模方式进行对比，得到按时间顺序建模预测精度较高的结论，但是因为考虑的影响因素较少，没有进行特征挖掘，得到的结论并不精准。深度学习方法预测过程简单、结果较为准确，近年来受到了广大学者的青睐。文献［12-13］中则利用了SVG 模型、玻尔兹曼机算法、梯度累积策略等深度学习方法对光伏出力进行分析与预测，得到了较为精确的预测结果，但由于没有考虑光伏出力的特征挖掘，预测精度还可有待提高。

本文提出深度学习方法中基于特征挖掘的门控循环单元网络和注意力机制（Gated Recurrent Unit-Attention，GRU-A）光伏发电功率预测模型。门控循环模型（Gated Recurrent Unit，GRU）是基于长短期记忆模型（Long Short-Term Memory，LSTM）的一种变体，它把LSTM的遗忘门和输入门合并成一个更新门，这样可以简化模型，使计算过程变得更加快速简单。但LSTM和GRU均无法表示隐层输出的重要性［14］。所以，文中在GRU的基础上加入了可以体现每个输出重要程度的注意力机制（Attention），赋予隐层不同的权重，处理长向量序列。将GRU模型和Attention模型结合起来，建立了GRU-A 光伏预测模型。最后，根据某个光伏电站的实际光伏数据进行仿真，仿真结果证明了基于特征挖掘的GRU-A 光伏发电功率预测模型相比于其他模型能得到更为精确的结果。

1 光伏出力特征构造

1.1 光伏实际功率与相关因素分析

由光伏发电原理可知，太阳实发辐照度与实际功率呈现正相关关系，光伏发电功率的实际大小很大程度上由实际辐照度决定。由图1 可以看出，实发辐照度与实际功率呈完全正相关，尤其在时间点50 和150前后，两条曲线完全重合，实发辐照度和实际功率大致成100 倍的关系（文中相关图片横坐标时间点的数据采样频率为15 min。）

图1 光伏实际功率与实发辐照度关系

图2 展示了光伏实际功率与温度的关系。可以看出两者之间并不是简单的正比例关系，当温度出现峰值时，光伏实际功率则会骤降至零，并在温度下降过程中，一直保持为零。

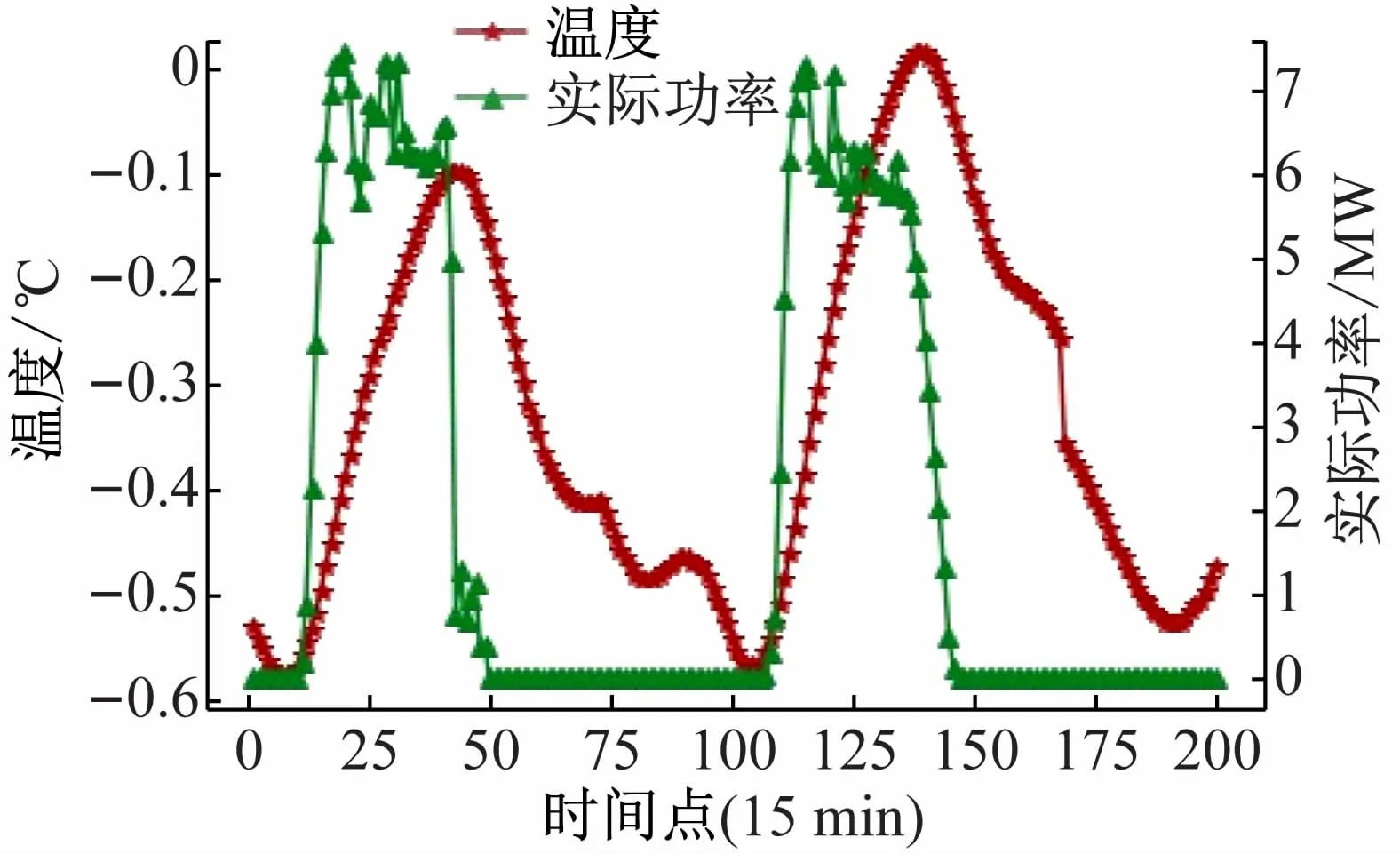
图2 光伏实际功率与温度关系

虽然实发辐照度与温度和实际功率呈线性关系，但湿度、风速、风向和压强与光伏实际出力并没有明显的线性关系，由图3 ～6 很难找到两条曲线的线性关系。除此之外，由辐照度、温度、湿度、风速、风向及压强构成的统计特征和多项式特征对光伏实际功率也存在一定影响。因此需要以这些特征为基础建立构造特征，以便模型能够更好地学习各个特征与光伏实际出力之间的关系。

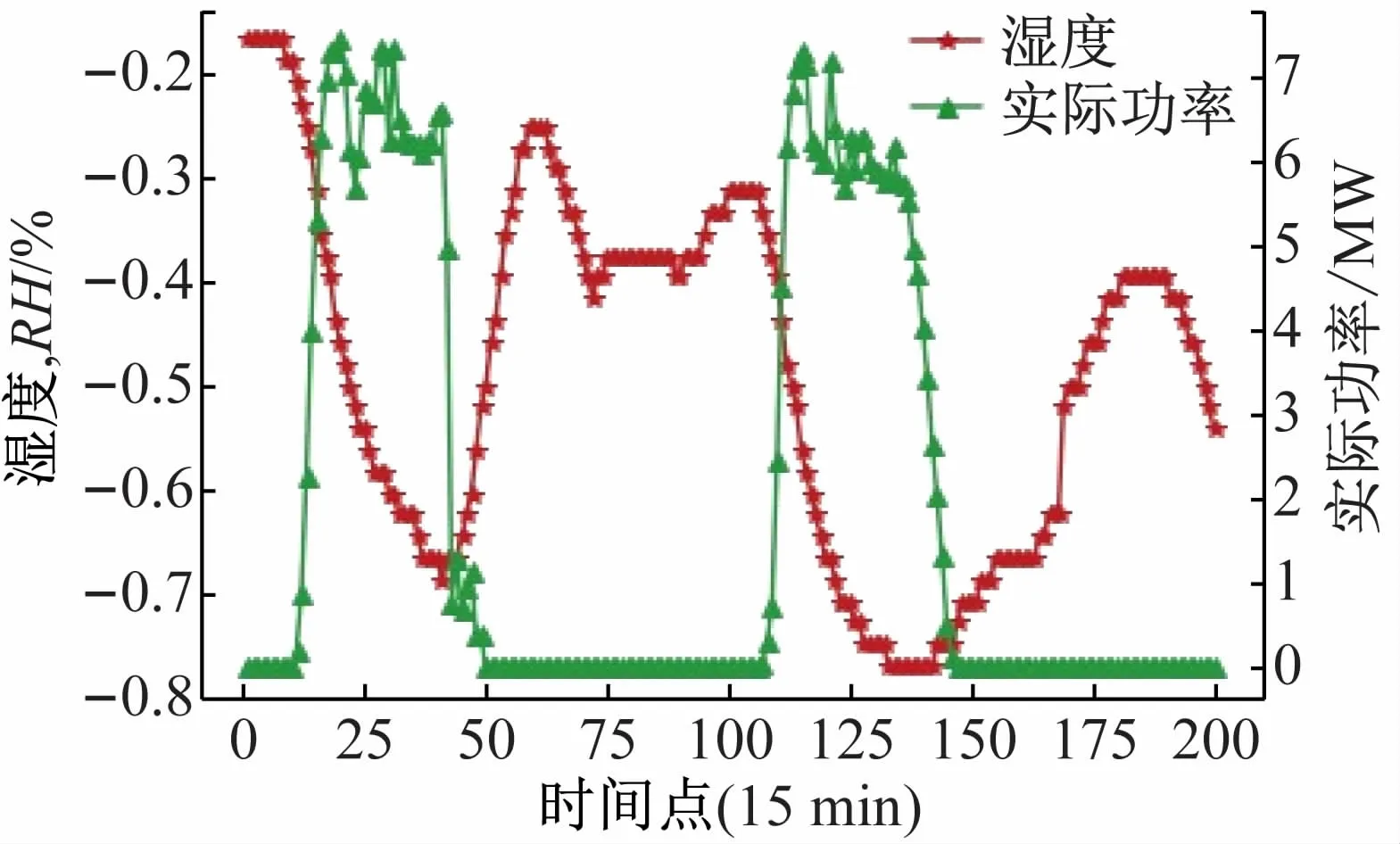
图3 光伏实际功率与湿度关系

图4 光伏实际功率与风速关系

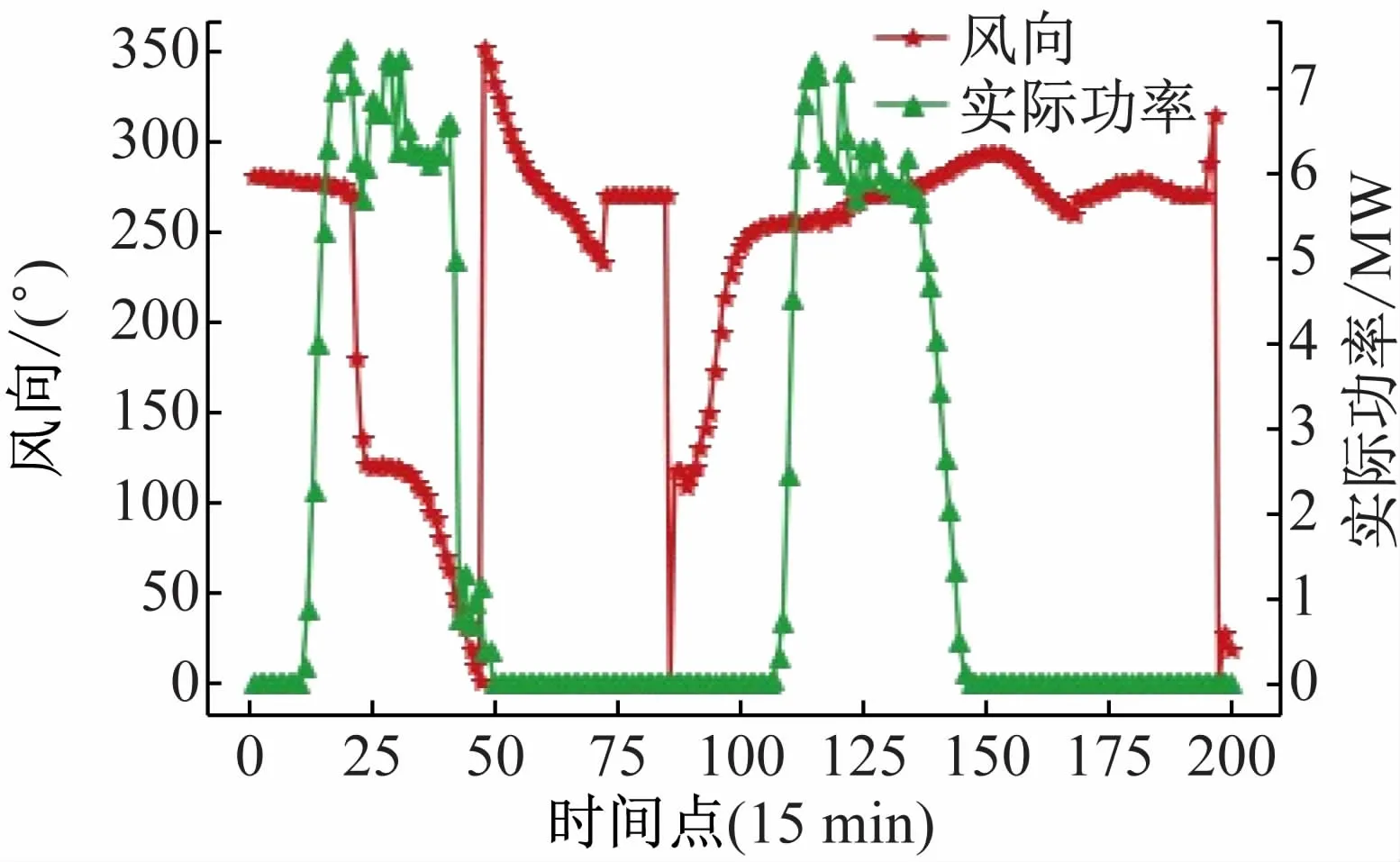
图5 光伏实际功率与风向关系

图6 光伏实际功率与压强关系

1.2 光伏实际功率预测特征构造

预测未来的光伏实际功率用到的数据都是未来的相关预测数据。温度、湿度、压强等和天气相关的预测数据都可以通过气象预报得到，但是预测辐照度（文中简称辐照度）就得通过图7 分析获得。从图中可以看出，辐照度具有较强的周期性规律，因此构造两种特征来表示这种周期性，即dis2peak和peak辐照度。前者代表距周期峰值的距离；后者代表辐照度峰值的实际值。

图7 dis2peak与peak辐照度特征构造方法

为了使模型预测更精确，需要考虑更多的影响因素。通过分析，在上文1.1 的基础上添加了时间特征、相关因素的均值、方差、平方等特征，以及每天的白天温差特征，还有各因素差值构造，例如白天温差就是当天白天最大温度和最小温度差值，其他因素差值做相同处理。

风速及大气湿度会影响太阳能光伏板表面的积灰程度，从而影响光伏出力。诸如此类的影响因素通过特征构造后共有132 个特征，这种特征构造对光伏出力的影响因素考虑全面，既能增加特征的非线性性，还可以发掘特征融合后对光伏发电功率的影响，使光伏预测更加精确。特征构造的方法是对相关因素之间进行多项式特征和统计特征构造，其中多项式特征的构造方法为：假设有特征a、b，则对应特征为1，a，b，ab等；统计特征的构造方法为：假设有特征a、b，则对应统计特征为amean，bmean，astd，bstd。

1.2.1 多项式特征

（1）a，b分别为各个特征的独立模型，如风速、风向、湿度、温度、辐照度、压强、白天温差等。

（2）特征a·b：辐照度·风速、风速·温度、温度·压强、风速·压强、辐照度·压强、风速·风向、辐照度std·风速mean、风速·风速、湿度·湿度、温度·温度等。

（3）特征a/b：辐照度/风速、风速/温度、温度/压强、风速/压强、辐照度/压强、风速/风向、辐照度std /风速std、湿度mean/风速mean等。

（4）特征a+b：辐照度+风速、风速+温度、温度+压强、风速+压强、辐照度+压强、风速+风向、辐照度std+风速mean等。

（5）特征a-b：辐照度-风速、风速-温度、温度-压强、风速-压强、辐照度-压强、风速-风向、风速mean-辐照度std等。

1.2.2 统计特征

（1）特征a或b的均值（mean）。如风速mean、湿度mean、温度mean、辐照度mean、压强mean、白天温差mean等。

（2）特征a或b的标准差（std）。如风速std、湿度std、温度std、辐照度std、压强std、白天温差std等。

文中考虑到的特征与其他现有文章相比更加全面，不再拘泥于几个因素，而是全方位地构造出了上百个特征，同等条件下，考虑的特征越多，则预测精度就越高。在预测模型建造好之后，构造好的特征将作为输入数据传送到预测模型中，以实现使文中光伏发电功率预测精度更高的目的。

2 基于GRU-A的光伏预测模型

2.1 GRU模型

GRU网络是一种比LSTM 网络更加简单、快速的循环神经网络，加进了门控机制来控制信息更新的方式。在LSTM原有的基础上引入了一个更新门来决定此刻状态从上一时刻状态中保留的信息量以及从候选状态中选取的信息量［15］。它的传递公式如下：

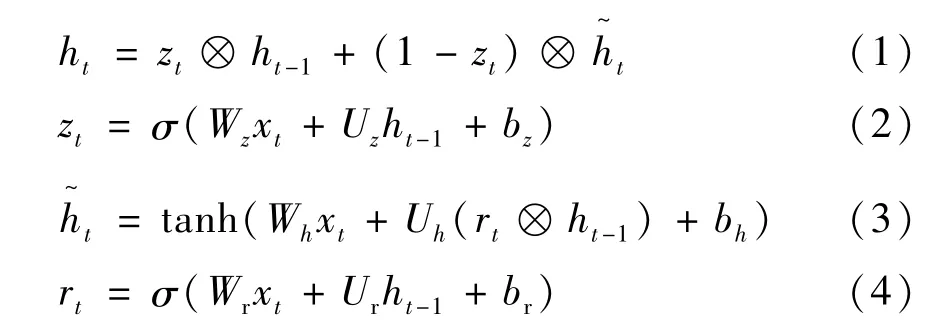
其中：

①Zt∈［0，1］是更新门，当Zt＝0 时，当前状态ht和前一时刻状态ht-1互为非线性函数关系；当Zt＝1时，当前状态ht和前一时刻状态ht-1互为线性函数关系，ht-1是上一时刻状态。⊗为向量乘积符号。

②ht是当前时刻的候选状态。rt∈［0，1］是重置门，用来控制ht的计算。当rt＝0 时，ht只和当前输入xt有关，和历史状态无关。当rt＝1 时，ht和当前输入xt与历史状态ht-1都有关。

③σ为Sigmoid函数；tanh为双曲正切函数。

由式（1）可以看出，Zt＝ 0，rt＝1 时，GRU 网络为简单循环网络；Zt＝0，rt＝0 时，ht只和xt有关，和ht-1无关；当Zt＝1 时，ht＝ht-1，和当前输入xt无关。

图8 为GRU循环单元结构，其中zt表示更新门，rt代表重置门。zt用于控制前一时刻的状态信息被带入到当前状态中的程度，zt的值越小，前一时刻的状态信息被带入到当前状态的就越少。rt控制前一状态的信息被传送到当前候选状态ht中的数量，rt越大，前一状态的信息被写入当前候选状态的就越多。

图8 GRU结构图

2.2 Attention模型

当需要处理大量输入数据时，就可以用注意力机制（Attention机制）来从大量信息中选择一些关键信息进行处理，这可以简化运算、减小神经网络的计算负担、节约计算机资源。注意力模型如图9 所示，其中x1，x2，x3，…为输入，h1，h2，h3，…为输出。

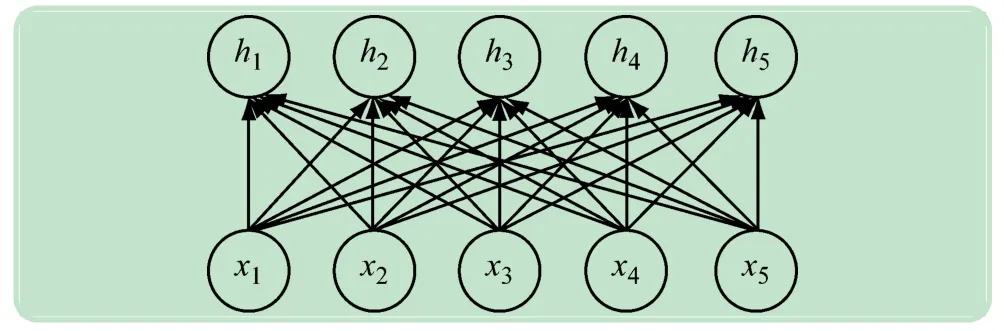
图9 注意力模型

Attention机制的计算可以分为两个步骤：① 在所有输入数据中计算注意力分布；②根据注意力分布来计算加权平均。这里选用自注意力模型作为输入的注意力模型。假设输入信息为x＝［x1，x2，…，xN，］∈，输出信息为，通过线性变换可以得到以下3 组向量序列：

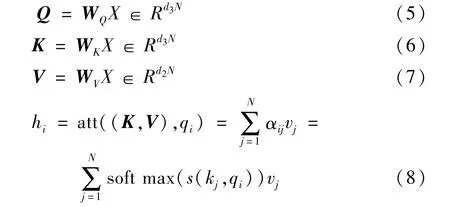
式中：Q是查询向量序列；K 是键向量序列；V 是值向量序列；WQ、WK、WV分别是可学习的参数矩阵；i，j∈［1，N］为输出和输入向量序列的位置，连接权重αij由注意力机制动态生成。

2.3 GRU-A模型

文中所提的GRU-A 模型结构如图10 所示。GRU-A模型使用上文中所搭建的特征群作为输入x1，x2，…，xi，通过GRU 模型进行计算得到对应输出h1，h2，…，hi，然后在隐藏层中利用Attention 机制计算各个输入的注意力概率分布值a1，a2，…，ai，输出层的输入是上一层Attention 层的输出。最后利用Softmax 函数对输出层的输入进行相应计算，从而得到下一时刻的光伏发电功率预测。

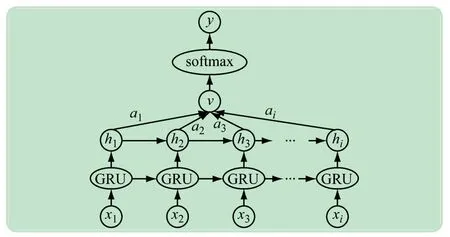
图10 GRU-A模型结构图

GRU-A模型的训练和测试流程图如图11 所示。将上文1.2 中提出经过特征挖掘工程处理后的特征如湿度、风速、辐照度、压强等作为输入传送进GRU-Attention网络，经过一系列计算最终可输出光伏功率的预测值。

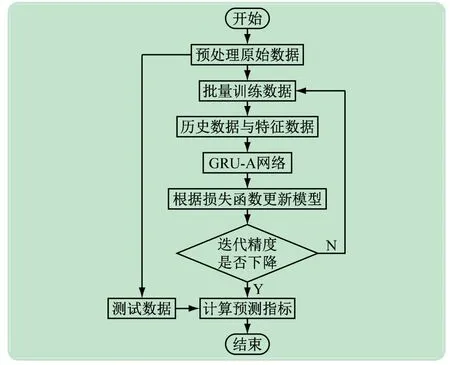
图11 模型预测流程

2.4 损失函数

模型参数的优化采用一阶Adam（Adaptive Moment Estimation）优化算法。此算法可以通过连续更新迭代网络神经元节点的权重和偏置使函数值降至最优值。在模型训练期间，根据训练输出和标准化实际功率计算GRU-A的损失MSE（Mean Squared Eorr），

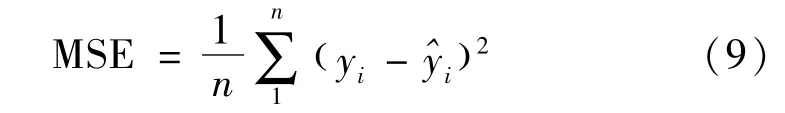
式中：n为样本数；yi为实际值；^yi为模型输出值。

3 光伏实际功率预测实验及结果分析

3.1 实验评价方法

光伏功率预测的评价指标选定如下：

R2（R-squared）可决系数

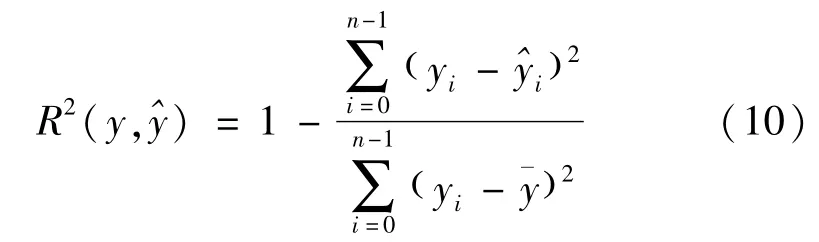
MAE（Mean Absolute Error）均方根误差

MAPE（Mean Absolute Percentage Error）相对百分误差绝对值的平均值

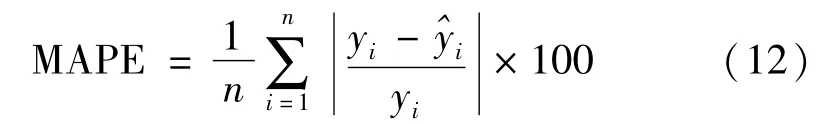
3.2 算例仿真与结果分析

根据某个光伏电站的实际光伏数据共41 853 条数据，数据采样频率为15 min，从2018-01-01 0：00：00开始直到2019-04-26 4：00：00。在cpu：i7-9 700K，gpu：2080Ti 11 GB，内存：16 GB 的计算机条件下进行。在41 853 条数据中选用33 853 条作为训练数据，剩余8 000 条作为测试数据。数据中包含了时间、辐照度（预测辐照度）和来自数字天气预报的风速、风向、温度、压强、湿度。采用下式对数据进行标准化，

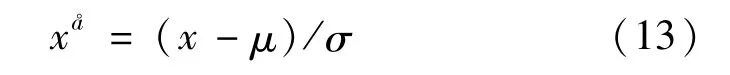
式中：μ是该特征的均值；σ是该列特征的方差。

文中采集了实际的光伏数据集对模型进行实验，选择LSTM、BP、SVR、GRU 预测模型与文中所提出的GRU-A预测模型进行结果对比。5 种模型的输入数据保持一致，均包括原始特征和经特征工程构造后的特征。这些特征组成输入特征矩阵，分别采用以上5 种模型进行建模训练和预测。由此可以验证特征工程构造的预测精度以及GRU-A 模型的优良性能。模型及其参数见表1，其中神经网络的参数代表其每层的单元数。

表1 各个模型参数

采用表1 中5 个模型分别对原始特征和特征工程构造后的特征进行建模，可得表2 给出的共8 000 个点的预测值平均MAE、R2、MAPE。经过对比可以看出，构造特征后的5 个模型的MAE、R2、MAPE 基本都有所提高，证明了对输入数据进行特征构造可以使模型精度显著提高。

表2 各个模型预测结果

表2 的预测结果中包含各类型复杂天气情况，由于光伏发电功率受天气影响随机波动性较大，有必要深入分析不同变化情况下的光伏实际预测情况。为了具体验证GRU-A模型的有效性，将不同天气下基于构造特征的模型的预测结果进行展示。由于夜晚不存在阳光，所以只关注早上6：00 到晚上18：00 的光伏发电功率。

图12 展示了晴天的光伏发电功率预测曲线图。如图所示，5 个模型都能拟合出实际光伏发电功率，拟合精度与稳定性却有较大差别。BP 模型的预测曲线和实际功率曲线走向稳定性比较一致，但精确度不够。SVR、BP、LSTM、GRU 4 个模型的预测曲线稳定性和精度均不佳。而GRU-A 的功率预测曲线和实际功率曲线最靠近，预测稳定性和精度都最好。

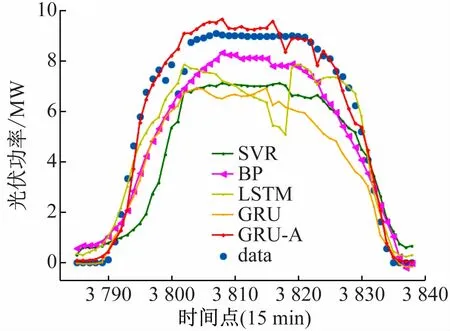
图12 晴天下光伏发电功率预测对比

图13 展示了复杂天气情况下（上午晴天下午阴天）的光伏功率预测结果。此时，只有GRU-A 预测模型曲线与实际功率曲线大致贴合，说明该算法在天气复杂时仍然能较好地预测光伏发电功率的变化情况。

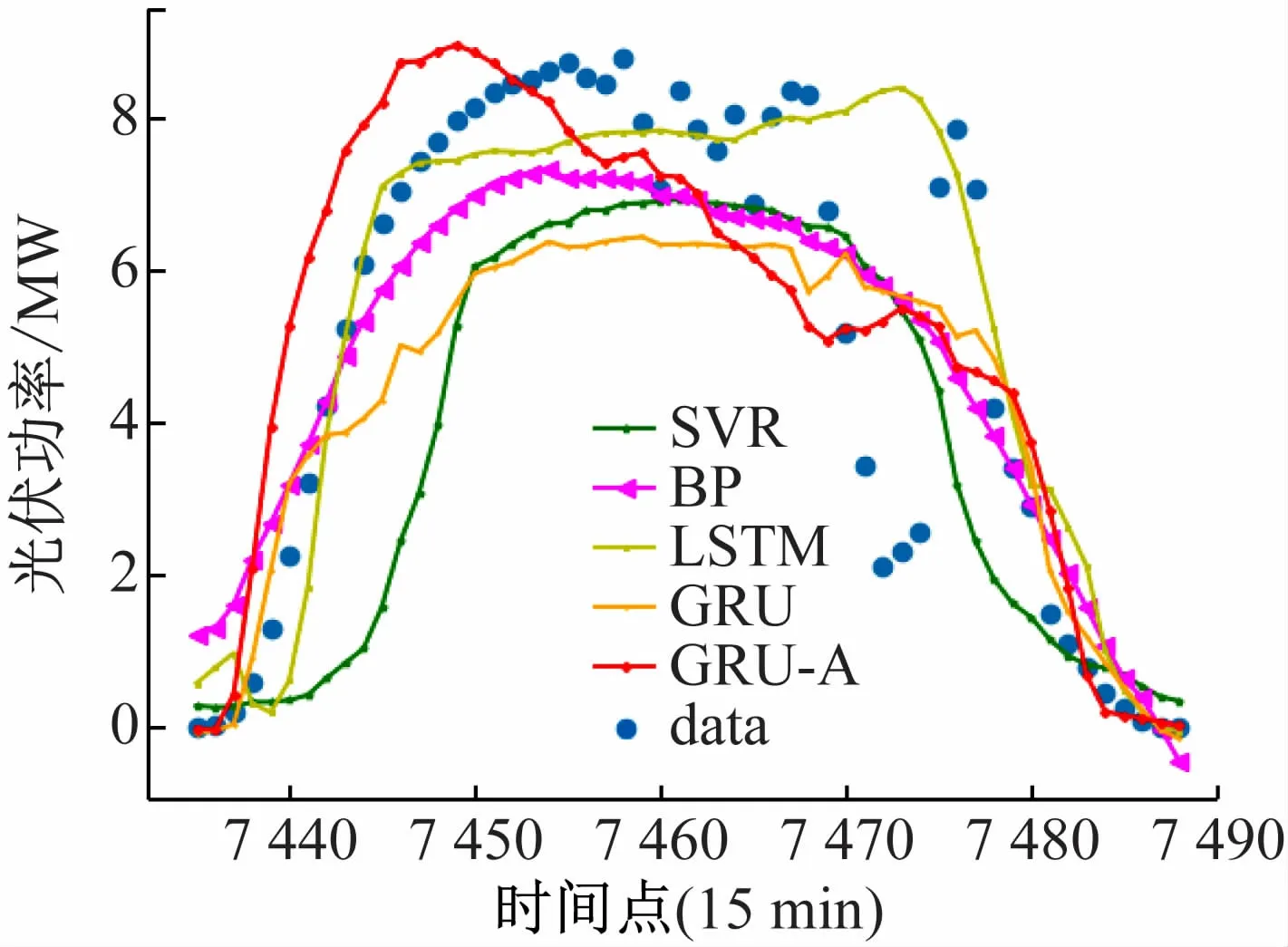
图13 天气变化下光伏发电功率预测对比

图14 展示了阴天情况下光伏功率预测情况，可看出，在此情况下只有GRU-A模型预测结果能大致拟合实际光伏发电功率。说明此类天气下，需要有记忆能力的模型来预测光伏发电功率才会更加准确。

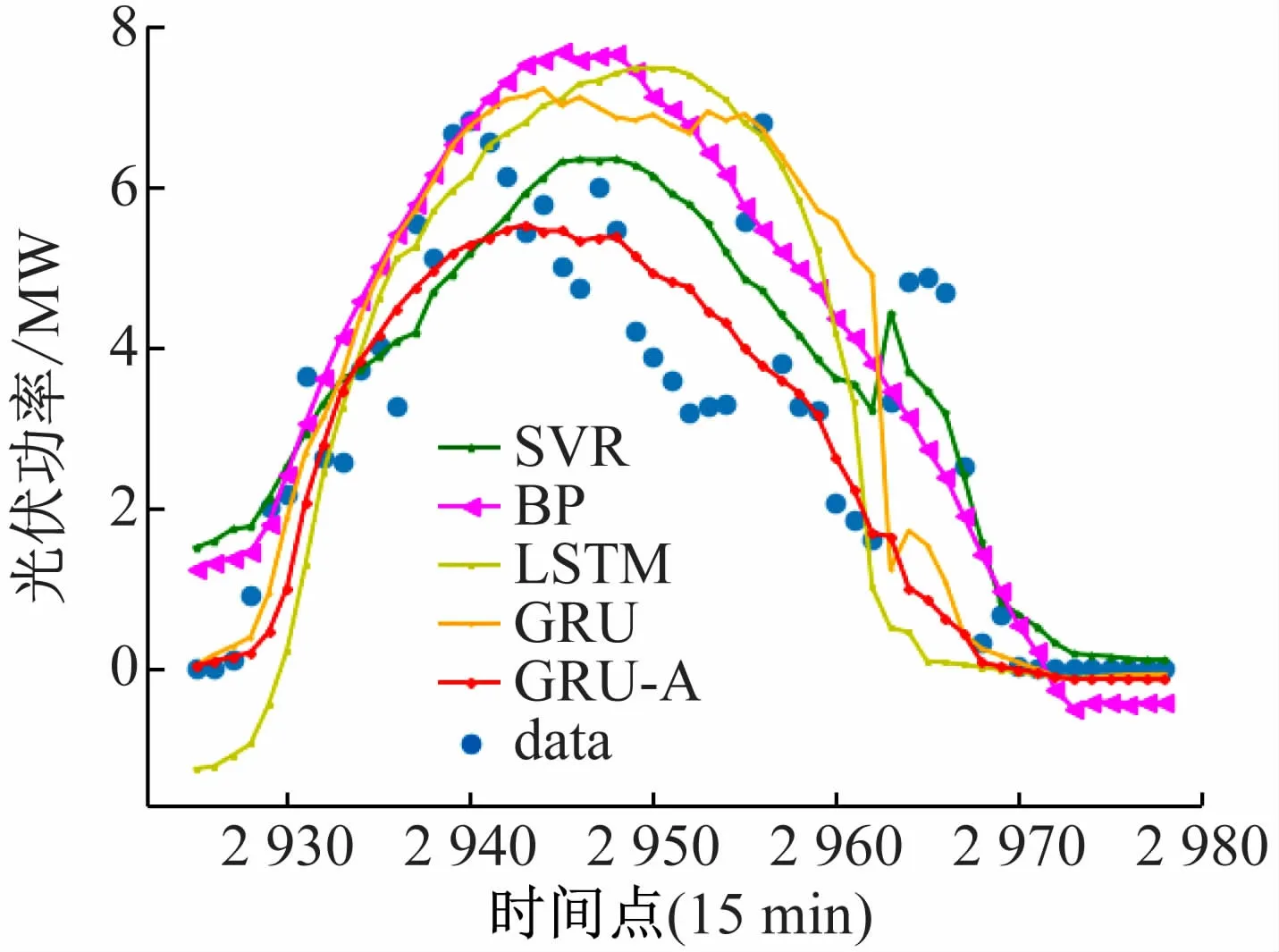
图14 阴天下光伏发电功率预测对比

将仿真结果绘制成表格形式如表3 所示，其中，“变天”指1 d当中天气在晴朗和阴天当中变换不定。对比分析可得，晴天时，GRU-A 模型预测结果的MAE和MAPE低了将近50%，而R2则与其他模型接近，显然，GRU-A预测模型性能最好。而当天气由晴好到变天时，其他模型的预测误差率增大了50%以上，只有GRU-A的误差率增大最少，变天情况下，误差率也最小。由此，天气复杂情况下，GRU-A 预测模型的预测性能最好。阴天时，GRU-A模型的3 项指标都比其他4 个模型好。由此可得，不论在何种天气情况下，GRU-A模型的预测准确率都比其他模型更高。

以上通过仿真实验曲线图和数据图表的形式对比了3 种不同天气情况下各个模型的光伏发电功率预测结果。对此结果进行对比分析，充分证明GRU-A模型可以获得更好的光伏发电功率预测指标和预测精度，既具有GRU模型的记忆能力，又比其他传统模型具有更好的泛化能力和稳定性，具有显著的优越性。

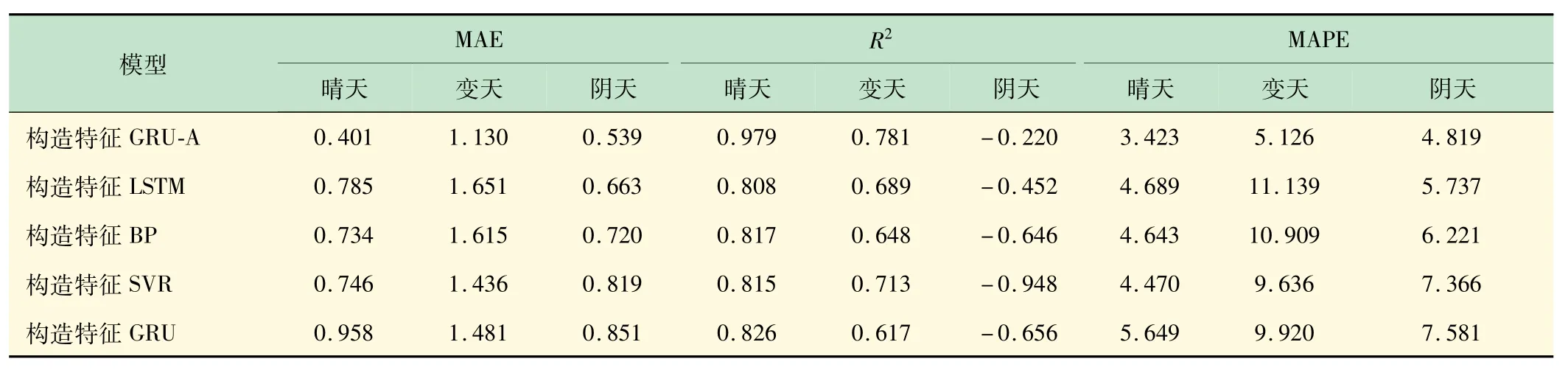
表3 不同天气下不同模型的预测参数

4 结 语

光伏发电功率受到天气状况、辐照度、温度、湿度等因素以及各因素组合等特征的影响，发电量的不稳定性会严重影响电网的调度质量、安全稳定运行及经济效益。因此提出了一种基于特征挖掘的GRU-A 模型的光伏发电功率预测模型。文中首先对影响因素进行特征构造，然后对比使用原始特征和构造后特征两种情况下各个模型的预测准确率，得出使用构造后特征会显著提高预测精确度的结论。最后通过仿真实验对比了使用构造后特征的各个模型在不同天气情况下的光伏预测情况，经过与其他模型的比较，证明了GRU-A模型有以下优点：① 具有很强的泛化能力、构造了统计特征与多项式特征使预测结果更加精确；②搭建的GRU-A模型使预测结果更加稳定精准，不论天气情况单一还是复杂多变，GRU-A模型都能够精确地预测光伏出力。总而言之，与其他传统模型相比，基于特征挖掘的GRU-A 光伏发电功率预测模型的预测精度更高、预测稳定性更好。