浅谈变式教学策略在初三数学教学中的运用

孙婉萍

摘  要：变式教学是教师对教学中的问题进行不同角度、不同层次、不同情形的变式，以暴露问题本质特征，展现不同知识间的内在联系的一种教学设计方法。在初三数学教学中运用变式教学策略，可以把学生从题海中解放出来，实现真正意义上的减负增效。本文阐述了一题多解、一题多变、多题归一的变式策略在教学中的應用，并提出变式教学的策略。

关键词：变式;教学策略;初三数学

近几年的数学中考试题不再是课本习题的简单再现，而是取材于课本，加以变换获得。这就要求教师在初三数学教学中，以课本知识为依托，进行变式教学，从而启发、训练、优化学生思维品质，提升学生的系统思维水平，培养学生解题能力，掌握学习方法。

一、变式与变式教学

变式是指有目的、有计划地对命题进行合理的转化，即保留对象中的本质属性，不断更换命题中的非本质特征，如变换问题中的条件或结论，转换问题的内容或形式，以迎合实际应用的各种环境。

数学变式教学就是通过从多个方面变更所提供数学对象素材或数学问题呈现形式，使事物的非本质特征时隐时现而其本质特征保持不变的教学形式。它是一种数学教学方法，也是一种数学教学思想。

那么如何运用数学变式策略，使课堂教学更高效？本文从亲身经历的案例出发，介绍变式策略和教学策略。

二﹑变式策略在数学教学中的运用

1.一题多解的方法性变式

一题多解，旨在对同一个问题从不同的角度，应用不同的方法进行求解，进而对几种方法进行比较，找到解决问题的最佳途径。这能实现解题方法的整理归纳，使知识融会贯通，让学生养成多角度观察理解事物的习惯，提高其思维的广阔性与灵活性。

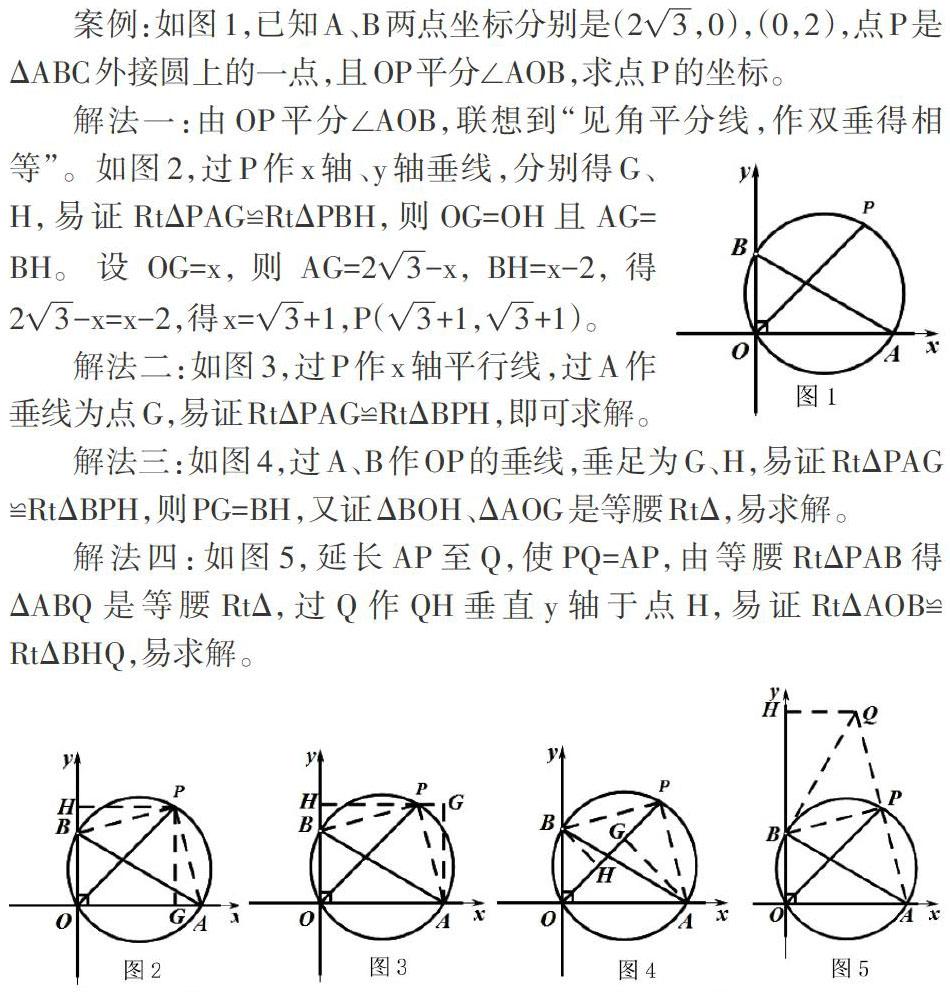
案例：如图1，已知A、B两点坐标分别是（2[3]，0），（0，2），点P是ΔABC外接圆上的一点，且OP平分∠AOB，求点P的坐标。

解法一：由OP平分∠AOB，联想到“见角平分线，作双垂得相等”。如图2，过P作x轴、y轴垂线，分别得G、H，易证RtΔPAG≌RtΔPBH，则OG=OH且AG=BH。设OG=x，则AG=2[3]-x，BH=x-2，得2[3]-x=x-2，得x=[3]+1，P（[3]+1，[3]+1）。

解法二：如图3，过P作x轴平行线，过A作垂线为点G，易证RtΔPAG≌RtΔBPH，即可求解。

解法三：如图4，过A、B作OP的垂线，垂足为G、H，易证RtΔPAG≌RtΔBPH，则PG=BH，又证ΔBOH、ΔAOG是等腰RtΔ，易求解。

解法四：如图5，延长AP至Q，使PQ=AP，由等腰RtΔPAB得ΔABQ是等腰RtΔ，过Q作QH垂直y轴于点H，易证RtΔAOB≌RtΔBHQ，易求解。

当然，本题还可以将ΔBOP绕点P按逆时针旋转90°至ΔAPQ，易证RtΔBPO≌RtΔAPQ，再证ΔPOQ等腰RtΔ而求解。以上一题多解的变式设计，可以帮助学生全面地复习构造一线三直角、旋转法造共直角顶点的双等腰直角三角形等方法。通过对这些方法的整理归纳，使学生在中考中能够以不变应万变，高效解题。

2.一题多变的开放性变式

开放性变式是从原题出发，运用逆向或横向思维，通过改变题目条件、结论、题型，或将问题进行等价替换等手段进行引申或改编，使原来的一道题变成一类题，再由一类题变为多类题，形成完整的知识体系。

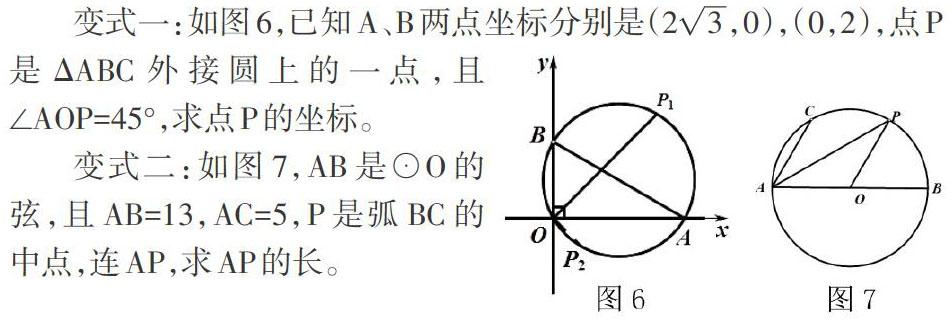
变式一：如图6，已知A、B两点坐标分别是（2[3]，0），（0，2），点P是ΔABC外接圆上的一点，且∠AOP=45°，求点P的坐标。

变式二：如图7，AB是⊙O的弦，且AB=13，AC=5，P是弧BC的中点，连AP，求AP的长。

变式一是将条件等价替换，变式二将条件弱化，但问题的本质不变。通过变式有效地引导学生在解决问题的过程中巩固知识、掌握方法，提升解题能力。

3.多题归一的强化性变式

多题归一指用同一知识和关系解决不同结构的题目，《数学课程标准》在几何方面的学习要求学生“能从较复杂的图形中分解出基本的图形，并能分析其中的基本元素及其关系，利用直观来进行思考”。变式二可以用案例的解法一和解法五求得。多题归一，加深学生对遇角平分线作双垂线、见等腰想旋转、见直角造一线三直角等解题方法的印象。教师在平时的教学中要引导学生建立基本图形库，从复杂图形中分离出基本模型，这是分析解决问题的先决条件，能起到化繁为简的效果。

三、变式教学运用策略

1.紧扣考纲，有的放矢

变式教学设计要有明确的指向和思维层次要求。初三毕业班教学内容多、时间短、难度高，在课堂教学过程中，只有按照既定的教学大纲设计变式，才能做到有的放矢，实现中考的标准化和科学化。

2.联系课本，循序渐进

课本中的例题具有较强代表性和典型性，教学中要善于借题发挥，从经典出发，向多方面延伸，既可以巩固老知识，又能推动新方法和新思维的学习和融合，起到事半功倍的效果。此外，难度适当、循序渐进的变式教学更有利于学生巩固知识，调动学生的学习积极性。

3.重视过程，活跃思维

教好数学的内涵是使学生在掌握数学知识的过程中学会思考，变式教学就是训练数学思维的过程。教师应注意解题思路的探索和解题方法的概括，使学生在解题过程中活跃思维，提升数学能力。

4.全员参与，共同提高

在教学中，教师不能“唱独角戏”，要鼓励学生参与变题。全员参与变题，不仅可以锻炼学生的思维能力，还可以提高学生的合作能力和说题能力，让不同层次的学生都得到全面的提高。

总之，要用好变式教学，教师除了要有变的意识，更重要的是要在平时教学过程中，肯下功夫研究教材和习题，将薄书读厚。只有这样才能帮助学生将厚书读薄，从题海中解放出来，实现真正意义上的减负增效。

参考文献

[1]徐方瞿.基本图形分析法[M].郑州：大象出版社，1998.

[2]万沈洁.提高中考数学复习课教学有效性的策略[J].中学课程辅导，2014（10）.