基于核密度估计的旋转机械损伤贝叶斯智能评价方法*

赵海心 姜孝谟 徐胜利 林 琳 宫云庆

（1.大连理工大学；2.沈阳鼓风机集团股份有限公司）

0 引言

旋转机械广泛应用于能源、化工、航空航天等诸多领域中。随着工业技术的发展，旋转机械日趋大型化、高速化和自动化，但同时带来了系统复杂度的增加，也增加了对系统可靠性的要求。旋转机械运行期间经常发生各种故障，导致整个生产非正常停止运行，产生巨大经济损失，严重时甚至会造成安全事故和人员伤亡[1-3]。因此，对旋转机械进行早期故障识别，对于避免重大事故，提高生产率和减少维修时间都具有重大现实意义[4-5]。

对传统旋转机械进行故障诊断的方法有解析模型方法[6]、专家系统方法[7]、人工智能方法[7-11]等。解析模型方法能够从机理上直接解释故障，但解析模型相对简单，难以用于复杂工程系统。专家系统利用了现有的知识和经验进行故障识别，但专家系统构建十分困难，需要复杂艰深的知识和长期积累的经验，构建好的专家系统也缺乏灵活性和可移植性。人工智能方法通过提取数据中的特征信息实现故障检测，更适用于目前工程系统中复杂的大量数据。在人工智能方法中，无故障模型方法是一种常用的技术[12-13]。通过健康数据训练得到系统识别模型，用来预测健康状况下系统的响应。通过比较实测数据与模型预测值，比如评估两组数的残差，来判断系统的健康状况。这种方法不需要系统的历史故障信息，同时残差代表系统实际性能相比正常性能的偏差，具有明确的物理意义，在故障识别中表现出了良好的效果[14]。

基于系统实际测量和预测响应之间残差的故障识别方法，通常还需要一个损伤评估准则和量化指标来评价系统的健康状态。传统方法经常使用相对均方根误差进行评价[15]。通过反复试验获得预先设定的评估阈值，当相对均方根误差超过预先设定的阈值时，系统被判断已经发生损伤。然而，反复试验花费高，并且试验存在随机误差和错误，造成数据的不完整性和不确定性，影响阈值的精度。Mahadevan等人[16]开发了基于贝叶斯假设检验的模型验证方法，利用测量数据，验证了贝叶斯方法能够有效解决模型验证中数据的不确定性。针对模型预测和传感器数据的不确定性，Jiang[17]提出了一种基于贝叶斯假设检验的结构损伤定量评估方法。这种基于贝叶斯推断的方法能够处理数据不确定性问题。但这种方法依赖于残差数据的正态分布假设，要求模型健康状况残差数据应符合0均值的正态分布，由于数据不确定性的存在，实际工程很难完全满足这一点，使基于正态分布假设贝叶斯方法的故障识别产生误报和错报。

针对这一问题，本文提出了一种基于核密度估计的贝叶斯假设检验方法。通过核密度估计得到实际数据和预测输出的残差分布，根据得到的分布，导出了贝叶斯因子的显式表达式。该方法不需要对数据进行任何分布假设，因此适用于不同的应用场景。

本文的其余结构如下：第1节简要介绍了系统识别模型、正态假设的贝叶斯评估算法和核密度估计方法；第2节介绍了基于长短期记忆网络（LSTM，Long Short-Term Memory）的系统识别模型；第3节详细推导了基于核密度估计的贝叶斯因子评估表达式；第4节给出了整体算法流程；第5节使用实际压缩机运行数据验证了方法的有效性；最后给出了结论。

1 基本方法介绍

传统的贝叶斯故障识别方法[17]包括三部分，1）使用无故障系统运行的健康数据，训练得到系统识别模型，2）使用系统识别模型，预测系统在未知健康状态下的响应，3）将实测数据与模型预测的残差当作系统或构件故障的主要特征，使用基于正态分布假设的贝叶斯因子方法获得系统或构件的健康置信度。代替正态分布假设，本文发展核密度估计方法来得到残差数据的实际分布，使贝叶斯故障识别方法具有更好的普适性。本节将介绍LSTM神经网络预测模型、基于正态假设的贝叶斯因子故障评价方法和核密度方法。

1.1 LSTM神经网络预测模型

LSTM[18]是循环神经网络（RNN，Recurrent Neural Network）[19]的一种变体结构。RNN是模拟时序数据的神经网络模型，由输入层、循环层和输出层组成。RNN最突出的特点是当前时刻的预测值不仅由本时刻输入数据决定，同时受之前时刻输入数据影响，展现出了动态时序行为，因此能够有效应用于时间序列预测问题。但RNN方法存在梯度消失问题，当前时刻预测值主要由近期时刻数据决定，远端数据影响很小。这样，无法利用远端时刻数据对模型参数进行修正，影响了预测的精度。为解决这一问题，研究者在RNN基础上，发展了LSTM方法。

LSTM在RNN的基础上增加了3个逻辑控制单元：输入门、遗忘门和输出门。通过门单元的逻辑控制，决定数据是否应该用来更新模型或被丢弃，克服了RNN梯度消失的缺点，体现出了更高的预测精度[20]。数学上，LSTM模型由以下几部分组成：

遗忘门：

输入门：

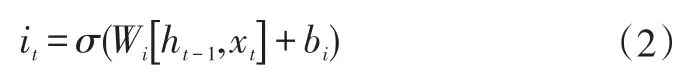
神经单元：

输出门：

最终输出：其中，Wf，Wi，Wc，Wo和bf，bi，bc，bo分别是各个门待训练的权函数和偏置；σ是sigmoid激活函数；ht是当前时刻的输出；ct是LSTM中的内置单元状态参数。从公式（3）中可以发现，LSTM将当前时刻的单元状态~ct和上一时刻的长期的记忆ct-1组合在一起，形成了新的单元状态ct，基于ct得到本时刻预测输出ht。通过遗忘门（公式1）和输入门（公式2），单元ct可以自由选择保存或丢弃当前时刻和久远时刻信息，而不是由时间距离长短决定影响程度大小，这样，导致的LSTM方法具有更高的预测精度。

1.2 基于正态分布假设的贝叶斯因子评估方法

假设ya={y1,a,y2,a…yn,a}和yb={y1,b,y2,b…yn,b}代表n个从时间序列a（预测模型数据）和b（所研究的系统或构件实测反应数据）获得的时序数据。令代表预测模型和实测数据的残差序列，其中ei=yi,a-yi,b，i=(1,2…n)是序列的差值。假设H0:a=b代表所研究的系统或构件健康，H1:a≠b代表所研究的系统或构件有故障。健康状况H0的置信度可以定义为Pr(H0|data)，即实际残差序列data下的健康概率。基于贝叶斯公式[21]可得：

则：

其中Pr(H0)和Pr(H1)代表了H0和H1的先验概率，一般从统计规律或工程经验中获得。设Pr(H0)=π0,Pr(H1)=π1,注意到有π1=1-π0，Pr(H1|data)=1-Pr(H0|data)，将其带入公式（7）中可得：

其中，B01被称为贝叶斯因子似然比；λ就是待求的系统健康状况置信度；可以用似然比B01的函数表示。因此，求解置信度λ可变为求解似然比B01的问题。通常情况下，如果B01＞1,所研究的系统或构件被认为是健康的。否则被认为是有故障的。为了获得B01，需要计算Pr(data|H0)和Pr(data|H1)，即在系统健康和有故障两种情况下残差数据data出现的概率。

为了对这两个概率进行求解,贝叶斯推断引入了正态分布假设[17]：在系统或构件健康状态下，残差数据应符合0均值正态分布，即data～N(0,σ2)。否则, 残差数据会符合非零均值正态分布，即data～N(u,σ2)，其中u是一个非零数，σ2是残差数据的方差。则Pr(data|H0)可以表示为：

其中，Pr(ei|0)代表N(0,σ2)分布中出现ei的概率，即N(0,σ2)概率密度函数中ei处的值。而Pr(data|H1)可以表示为：

其中：

f(u|H1)代表了故障情况下u的分布概率函数。传

统方法认为u～N(0,σ2)。则B01可以表示为：

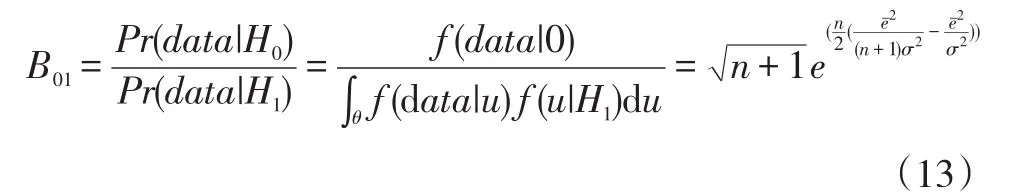
1.3 核密度估计方法

核密度估计（Kernel Density Estimation）[21]是一种非参数估计方法，用于拟合数据的分布密度函数，无需对分布类型进行任何假设。核密度估计表示如下：

其中，n是待估计点的个数；h是核密度函数的带宽参数；K(·)是核函数。常用的核函数有均匀函数、三角函数和高斯函数。均匀核和三角核都是分段函数，而高斯核是连续函数，连续函数使得数据分布的拟合更加平滑。因此，在本文的核密度估计中，采用高斯函数作为核函数，表达式如下所示：

核密度估计将每个待测点的出现位置看成一个分布，局部核函数K(x)代表其概率密度分布，K(x)在点实际出现位置概率最高。全局分布密度函数可视为所有待测点局部核函数的叠加，如图1所示。

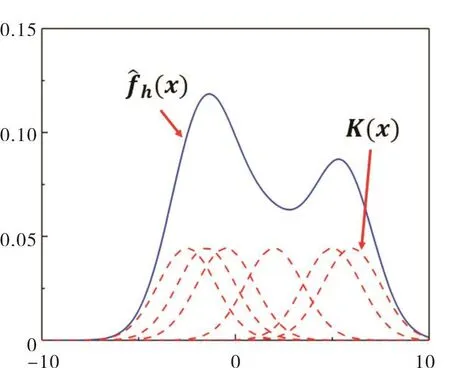
图1 核密度估计原理Fig.1 Principle of kernel density estimation

带宽h也是影响分布拟合效果的重要参数。理论上，当h趋于零时，它接近于数据的真实分布。但是，h值太小会导致分布函数不够光滑。本文通过最小化数据和拟合曲线之间的平均积分平方误差（MISE）[22]来确定带宽h的值。

2 LSTM预测模型构建

本研究发展一个双层深度学习神经网络LSTM模型用于预测系统反应。如图2所示，模型的隐藏层采用LSTM细胞和Dropout搭建双层循环神经网络。隐藏层的每个LSTM层后面增加一个Dropout层，这样在前向传播时，可以让神经元的激活值以指定的概率停止工作，从而增强模型的泛化性，防止过拟合。LSTM神经网络模块的层数越多，其学习能力越强，但是层数过多又会造成网络训练难以收敛，因此，本研究发展一个2层LSTM网络模型进行系统反应预测。输出层使用全连接层（Dense）对结果进行降维，并经过激活函数层（Activation）得出预测结果。损失函数选用均方误差，网络训练采用Adam优化算法[23]。

图2 预测模型结构Fig.2 The structure of prediction model

3 基于核密度估计的贝叶斯因子评估方法

由公式（9）可知，为了计算似然比B01，需要计算条件分布可能值Pr(data|H0)和Pr(data|H1)。本节介绍基于核密度估计的Pr(data|H0)和Pr(data|H1)计算方法，并给出最终似然比B01表达式。

3.1 健康状态下残差数据出现概率Pr(data|H0)

根据公式（10），Pr(data|H0)可以表示为：

其中Pr(ei|H0)代表系统或构件在健康状态下差值ei的出现概率，可以表示为：

其中，fH0(ei)代表了系统或构件在健康状况下残差数据概率密度函数中ei处的值。概率密度函数可以通过核密度方法训练健康数据的残差获得。假设健康数据残差为ex=(ex1,ex2,...exn),根据公式（14）和（15），基于健康残差数据获得的分布概率密度函数为：

带入式（16）中可得：

其中，h是通过最小化MISE方法[22]获得的带宽；ei是待测残差数据；xj是用于训练分布所用的健康残差数据。

3.2 故障状态下残差数据出现概率Pr(data|H1)

与Pr(data|H0)类似，Pr(data|H1)可表示为：

其中，Pr(ei|H1)代表故障状态下ei的出现概率:

其中，fH1(·)概率密度函数，表示故障状态下数据出现位置的分布概率密度。在本研究中，我们参考传统方法[17]的故障假设：故障状态数据分布与健康状态分布方差相同，故障只导致均值不一样。下面我们推导核密度估计的均值和方差表达式，确定故障状态数据分布的具体表示方法。

核密度估计分布的均值表达式如下：

其中，f(ex)是公式（13）中核密度估计得到的分布概率密度函数。经过推导，可以得到：

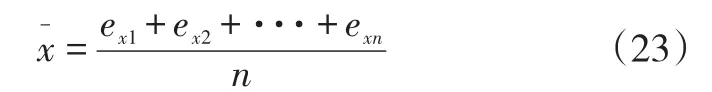
核密度估计得到的分布均值和所有训练点的均值相同。

同理可以给出核密度估计分布的方差表达式：

推导可得：

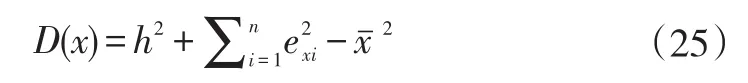
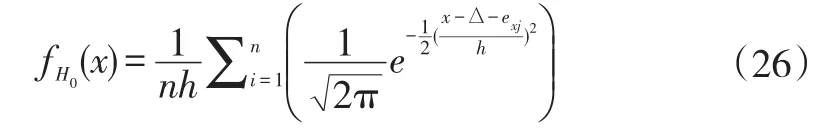
则新的均值和方差为：

其中f(∆|H1)是偏离均值∆在故障状态下的分布概率密度。似然比B01可表示为：

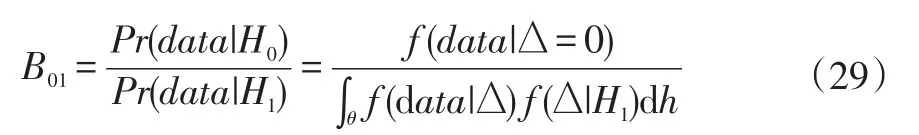
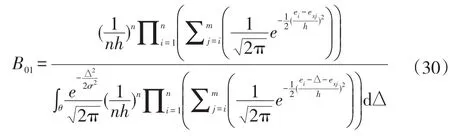
4 算法流程图

整个算法的流程如图3所示，我们将健康数据分为两部分，一部分数据用来训练预测模型，然后使用预测模型对另一部分数据进行预测，得到健康状态下的残差数据。使用预测模型对系统状态不知的实测数据进行预测，得到实测的残差数据。使用核密度估计方法训练健康状态残差数据得到健康残差分布。使用健康残差分布构建基于实际健康数据分布的贝叶斯估计方法。将实际残差数据代入贝叶斯方法得到系统目前的健康概率。

图3 算法流程Fig.3 Algorithm flow

5 算例验证

5.1 数据介绍

使用一组从转速5 556r/min的实际运行离心压缩机收集的数据，通过比较研究，对所发展的新方法进行效果验证。由于压缩机一个叶片断裂，导致该压缩机非正常停运。这算例使用压缩机失效前的数据来进行显示新方法的有效性。压缩机的传感器测点位置如图4所示，包含11个变量（两个轴承温度变量），测点之间间隔为1h。为比较算例验证效果，分别选择了早期健康运行时段1 600个点和故障开始发生时段400个点。其中50%的健康数据用于预测模型构建，25%的健康数据用于核密度估计训练分布函数，25%健康数据和所有故障数据用于故障状态识别。

图4 传感器位置与类型Fig.4 Position type of sensors

5.2 预测模型构建

预测模型的输入数据为除轴振动外10个变量的时间序列数据，输出为轴振动数据，即使用进口压力、出口压力等性能预测当前时刻轴振动。使用轴径向振动偏差信息作为故障的主要描述特征。训练前对10个变量数据分别进行归一化，将数据线性映射至0-Pr(H1|data)Pr(data)=Pr(data|H1)Pr(H1)1范围内。图5显示了算例的预测模型，以第一层LSTM的输入为例，图中（None，10，1）代表了输入的维度，None表示网络可输入任意个数的样本，（10,1）代表了每个输入样本是一个10×1的向量。

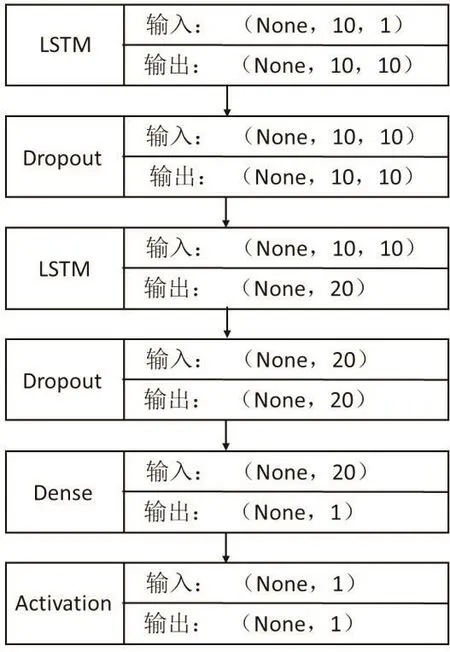
图5 算例预测模型Fig.5 Prediction model of example

5.3 方法比较

5.3.1 健康状态

使用健康数据，本节比较了提出的基于核密度估计分布和传统基于正态假设的贝叶斯评估方法。贝叶斯方法需要指定压缩机的先验健康概率，本文将先验概率设为π0=50%。采用试错法，选择固定宽度L=100的滑动窗口，根据窗口中的数据，使用公式（8）计算压缩机的健康概率。宽度L需要保持一定长度，如果L太小，待评估的数据过少，评估过于敏感。经过反复试验，我们得到L=100是区分健康和故障状态的合适值。滑动窗口每次移动一个测点来进行重复计算。图6是健康数据下两种方法的置信度比较，蓝色实线是核密度估计健康概率，红色虚线是传统方法健康概率。

图6 健康数据下两种方法置信度比较Fig.6 Comparison of confidence between two methods in health data

可以看出，本文提出方法置信度曲线局部存在一些波动，但整体健康概率均大于50%，说明新方法判断当时压缩机处于健康状态，波动是数据的不确定性导致的。传统方法波动程度更高，特别是对部分波动比较大的点，健康概率小于50%，产生故障报警。实际上该数据下压缩机处于健康状态，新方法判断更为准确。

图7是预测模型的预测数据和实际数据的对比，实线代表预测模型，点划线代表实测数据，图像显示模型预测结果跟实际数据的趋势十分吻合。图8是预测模型和实测数据残差的分布直方图。可以看出，即使对于健康数据，其残差同样不符合0均值的正态分布，出现了均值偏离。偏离可能是由于预测模型和外界环境的不确定性导致的。

图7 健康状况下预测模型和实测数据对比Fig.7 Comparison between prediction model and measured data under health condition

图8 待测健康残差数据分布直方图Fig.8 Distribution histogram of residual in health data

图9是用作核密度估计训练数据的分布直方图，可以看出，训练数据同样出现均值偏离，且偏离方向与待测健康数据一致，数据分布十分相似。核密度估计通过训练实际健康数据得到了这种偏离分布，并将其识别为健康状态；传统方法使用0均值正态假设，将这种均值偏离识别为故障状态，在偏离较大的部分产生报警，这是两种算法结果差别的主要原因。本文提出的基于核密度的贝叶斯故障评估算法误报率更低，适合复杂实际工程问题。

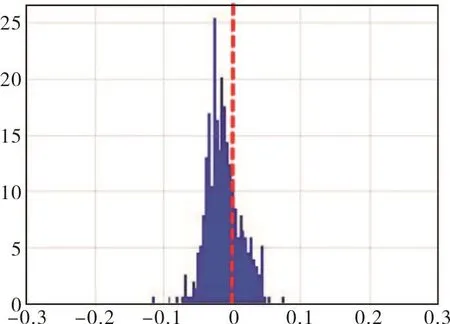
图9 核密度训练用残差数据分布直方图Fig.9 Histogram of residual data distribution for kernel density training

5.3.2 故障数据

使用故障开始发生时的数据对比两种方法对故障的识别效果。所有模型设置与5.3.1节中相同。图10是比较结果，蓝色实线是本文方法的置信度曲线，红色虚线是传统方法的置信度曲线。

图10 健康数据下两种方法置信度对比Fig.10 Comparison of confidence between two methods in fault data

可以看出，在故障开始阶段，两种方法置信度呈一直下降趋势，最终下降到0%，说明两种方法均判断压缩机处于故障状态。

图11是预测模型的预测数据和实际数据的对比，实线代表预测模型，点划线代表实测数据。

图11 故障状态预测模型和实测数据对比Fig.11 Comparison between predicted model and measured data in fault state

图12是残差数据的分布直方图。可以看出，故障数据残差均值出现明显偏离，且其分布相对健康数据的偏离方向不同，分布具有较大差别。传统方法将均值偏离识别为故障状态，核密度方法将两种残差数据的分布差别识别为故障状态，两种方法使用不同的方法确定故障状态，因此其置信度下降曲线存在区别。但两者均可以很好的完成对故障状态的识别。

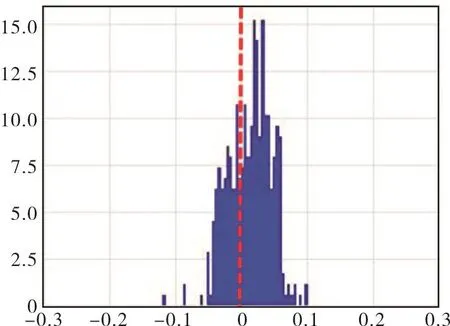
图12 待测故障残差数据分布直方图Fig.12 Distribution histogram of residual error of fault data

6 结论

本文发展了一个长短记忆神经元深度学习模型，预测旋转机械实际运行参数，并提出了一种基于核密度估计和假设检验的贝叶斯评估方法，可用于定量评估旋转机械的健康状况。传统的贝叶斯似然比通常是从正态分布假设中显式推导出来的，未能考虑到实际工程中不确定性带来的影响。本文从贝叶斯假设检验和核密度估计方法出发，在不考虑数据分布的前提下，推导了似然比。使用实际的压缩机运行数据，通过比较研究，对算法进行了定量评估。两个结果如下：

1）对于健康状态，该方法能够有效识别出健康数据的分布，识别精度优于传统方法，可有效降低误报率。

2）对于故障状态，两种方法均可以对故障进行有效识别。

目前所提出的方法仅限于单维数据的置信度估计，笔者将把提出的新方法扩展到多变量情况，并进一步讨论算法中各个参数对旋转机械损伤识别效果的影响。