化归思想下的高等数学教学

张汉清

(山西省财政税务专科学校,山西 太原 030024)

数学以其高度的抽象性和应用的广泛性而独立于其他自然科学,与一般的科学家相比,数学家在思维方法上是否有其独特的地方呢?一个可能的回答是:数学家特别善于使用化归的方法来思考问题和解决问题。也就是说,在思考和解决问题时,数学家往往不是对问题进行直接的攻击,而是对其进行变形、转化,直到最终把它化归成某个已经解决的问题。匈牙利著名女数学家路莎·彼得(Rozsa Peter)在其名著《无穷的玩艺》中曾对化归做过风趣的描述:“从陈旧的实用观点来看,以下的一个比拟也许是十分可笑的,但这一比拟在数学家中却是广为流传的:‘现有煤气灶、水龙头、水壶和火柴摆在您面前,当您要烧水时,应当怎样去做呢?’‘往水壶里注满水,点燃煤气,然后把水壶放到煤气灶上。’‘您对问题的回答是正确的,现把所说的问题稍作修改,即假设水壶中已经盛满了水,其他情况都不变,试问,此时您应当怎样去做?’被问者一定会大声而颇有把握地回答‘点燃煤气,再把水壶放到煤气灶上。’他确信这样的回答是正确的。但是更完善的回答应该是:‘只有物理学家才会按照刚才所说的办法去做,而数学家们却会回答:只须把水壶中的水倒掉,问题就化归为前面所说的问题了。’” 这个例子非常生动地说明了化归的本质和精髓,而且一针见血地指出数学家和其他科学家的思维的不同之处。

一、化归的客观背景

化归之所以成为数学的基本思想方法之一,有其理论上的客观背景。

众所周知,数学是一门演绎推理的学科,于是在同一个数学分支内部,或建立在同一个理论基础上的几个数学分支内部,就存在如下的事实:任何一个正确的结论都可按照需要与可能成为推断其他结论的依据。这表明在任何一个数学系统的展开中,都有形或无形地存在如下的结论链，见图1。

图1 数学推理框图

当然图1的表达形式只是一个大致的图示,不是完整而全面的,事实上,一个数学系统的“结论集”往往是一个树形的偏序集,而并非直线型的全序集;此外图中的“→”往往还是可逆的。

结论链的存在势必大大加快演绎推理的步伐。因此我们大可不必事事都去回到原始概念与推理工具,只需把待解决的问题转化为结论链中的某一环节就可以了。这就是化归方法在理论上的客观背景以及化归之所以能在数学领域大行其道的根本原因。

二、化归的方向——由未知到已知,由难到易,由繁到简

用化归法解决问题时,一个必要的条件是:和原来的问题相比,化归后所得的新问题必须是已经解决了的,或者是较为容易、较为简单的。这也就是说,化归的方向应是:由未知到已知,由难到易,由繁到简。这种化归在高等数学中贯穿始终,是微积分知识展开过程的主旋律。

从宏观来看,导数从其定义可知是一种特殊的极限,因此导数可归结为极限;定积分的计算通过牛顿—莱布尼兹公式归结为不定积分;微分方程也可化归为不定积分;重积分、曲线积分和曲面积分又都可化归为定积分来计算。

从微观来看,我们在进行复杂的极限、导数和积分的计算时,往往要通过恒等变形或借助有关的定理或法则,直到把待解决的问题转化为若干个已知的基本的极限、导数和积分的公式为止,即可求得原问题的解决。

例1 由于以下五种特殊类型的有理函数的积分问题已经得到了解决:

anxn+a1xn-1+…an-1x+an;

(其中n是正整数,a,b,c,…是任意实数)

而一般有理函数利用待定系数法可表示成这五种函数的线性组合(即分解成所谓的“部分分式”),因此有理函数的积分问题就可以得到解决了。

例2 对常数和三角函数只施行四则运算,所得出的式子称为三角函数的有理式。利用“万能公式”:

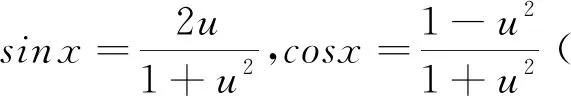
可以把任一三角函数的有理式化为u的有理函数,由于有理函数的积分问题已经解决,因此三角函数的有理式的积分问题也就彻底解决了。

例3 常系数线性微分方程(y(n)+p1y(n-1)+…+pny=0)可通过相应的代数方程——特征方程(λn+p1λn-1+…+pn=0)来求解。如图2所示。

图2 常系数线性微分方程求解框图

三、化归的方法——求变,映射,构造

虽然化归的大方向是确定的,但就化归法的具体运用而言,关键的问题显然在于如何实现化归,数学中用以实现化归的方法很多,这里仅对高等数学中常用的几种方法加以介绍。

(一)求变

在高等数学的计算中经常利用简单的解析式恒等变形,前述一般有理函数以及三角函数的有理式的积分,主要是利用了解析式的恒等变形;而更一般的积分问题要利用换元积分和分部积分法,亦即利用这两个积分法对积分进行恒等变形,以达到化难为易、化繁为简、化未知为已知的目的,我们把这种方法称为“变形法”。

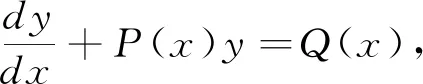
上述求解过程,首先解一个与原方程相关的特殊而简单的方程——齐次方程,得出其通解后,把其通解中的常数C“变易”为函数C(x),从而求得了原方程的通解。通过“求变”,实现了由一般到特殊,由未知到已知的化归。

(二)映射

映射法是用以实现化归的一种重要方法。简单地说,映射就是指在两类数学对象或两个数学集合的元素之间建立某种“对应关系”。利用映射法解决问题的过程是:首先通过映射f将原来的问题A转化为问题A′;然后在求得了问题A′的解x′以后,又通过反演φ求得原问题A的解x。如图3所示。

图3 映射法框图

例5 映射法在微积分中典型的应用是不定积分的“换元积分法”。运用第一换元积分法的步骤为:

其中，第二步和第四步分别是映射和反演。

运用第二换元积分法的步骤为:

F(t)+C回代：t=φ-1(x)F[φ-1(x)]+C

其中,第一步和第三步分别是映射和反演。

“换元积分法”的核心思想是通过换元(映射)把未知的或复杂的积分问题化归为已知的或简单的积分问题,再通过回代(反演)求得原问题的解。

例6 已知:eba。

直接证明这个不等式是很困难的,可采用映射法进行化归。

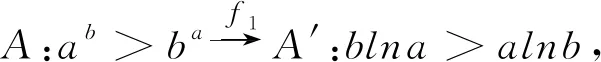
可知f(x)在(e,+∞)为减函数。再反演回去:

(三)构造

“构造”是实现化归的又一种重要方法。数学中所谓的“构造”是指利用问题的特殊性给所解决的问题设计一个“框架”。这里的“框架”含义甚为广泛,它可以是一个图形,一个方程,一个函数,也可以是一个与原命题相关的命题。其中构造函数在微积分中的运用非常普遍,在例5我们已经介绍了,再举数例进行说明。

例7 在微积分中有三个著名的中值定理,分别为:

罗尔定理。如果函数f(x)在[a,b]上连续,在[a,b]内可导,且f(a)=f(b),则在区间(a,b)内至少存在一点ξ,使得f′(ξ)=0。

拉格朗日定理。如果函数f(x)在[a,b]上连续,在(a,b)内可导,则在区间(a,b)内至少存在一点ξ,使得f(b)-f(a)=f′(ξ)(b-a)。

柯西定理。如果函数f(x)与g(x)均在区间[a,b]上连续,在(a,b)内可导,且在(a,b)内g′(x)≠0,则在(a,b)内至少存在一点ξ,使得

例8 拉格朗日定理又有两个重要的推论:

推论1 如果函数y=f(x)在区间(a,b)内任一点的导数f′(x)都等于零,则在(a,b)内f(x)是一个常数。

推论2 如果函数f(x)与函数g(x)在区间(a,b)内的导数处处相等,即f′(x)=g′(x),则f(x)与g(x)在区间(a,b)内只相差一个常数,即f(x)=g(x)+c。

推论1 可化归为拉格朗日定理得到证明;对于推论2,只需构造函数h(x)=f(x)-g(x)即可化归为推论1得到证明。

例9 设a,b,c为任意实数,证明方程4ax3+3bx2+2cx=a+b+c在0与1之间至少有一个实根。

由于参数a,b,c没有任何特性,所以试图利用介值定理给出证明的尝试将会陷入困境,而关于方程根的存在的定理还可以借助罗尔定理,构造函数f(x)=ax4+bx3+cx2-(a+b+c)x。

由于f(0)=f(1)=0,且f(x)在[0,1]上连续,在(0,1)内可导,f′(x)=4ax3+3bx2+2cx-(a+b+c)由罗尔定理可知存在点x0∈(0,1),使f′(x0)=0,此x0即为4ax3+3bx2+2cx=a+b+c在0与1之间的实根。

四、化归思路的产生——观察,类比,联想

我们知道,无论是一个成熟的数学分支还是一个已经获解的数学问题,都是通过演绎展开的。但无论是考察某一数学分支的展开过程或者是分析一个问题求解的过程,不难发现,演绎推理不过是人们在抓到真理之后,再补行的论证手续,因而演绎推理并不是发现和创新的重要手段。对于寻找真理、发现真理和探索求解方案而言,更重要的是实验、观察、归纳、类比和联想等方法。

在我们运用化归方法求解问题的过程中,观察、类比和联想同样起着非常重要的作用,它们从各个方面帮助我们确定化归方向,或启发证明或求解方法,找到正确的求解思路。如在例9中,首先通过观察所给方程的特点,联想到4x3,3x2,2x,a+b+c分别是x4,x3,x2,(a+b+c)x的导数,并联想罗尔定理,因而构造函数f(x)=ax4+bx3+cx2-(a+b+c)x,对其在[0,1]上应用罗尔定理,从而成功实现了化归。

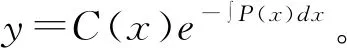
通过以上分析不难看出，观察、类比、联想是化归思路产生的重要思维过程,由精细的观察产生丰富而有效的类比和联想,从而发现化归的方向和实现途径。但是类比和联想都属于“合情推理”的范畴,其可靠性和有效性,必须经过严格的检验。如上述分析中,虽然我们猜出了非齐次方程的形式,但只有真正求出C(x),才可以检验我们猜想的正确性,如果C(x)无法求出或根本就不存在,那么我们的猜想和整个思路也就失败了。